(Feb 23: I have a new article that covers the technical details of mining. If you like this article, check out my mining article too.)
This blog post starts with a quick overview of Bitcoin and then jumps into the low-level details: creating a Bitcoin address, making a transaction, signing the transaction, feeding the transaction into the peer-to-peer network, and observing the results.
A quick overview of Bitcoin
I'll start with a quick overview of how Bitcoin works[2], before diving into the details. Bitcoin is a relatively new digital currency[3] that can be transmitted across the Internet. You can buy bitcoins[4] with dollars or other traditional money from sites such as Coinbase
To simplify slightly, bitcoins consist of entries in a distributed database that keeps track of the ownership of bitcoins.
Unlike a bank, bitcoins are not tied to users or accounts. Instead bitcoins are owned by a Bitcoin address, for example 1KKKK6N21XKo48zWKuQKXdvSsCf95ibHFa.
Bitcoin transactions
A transaction is the mechanism for spending bitcoins. In a transaction, the owner of some bitcoins transfers ownership to a new address.A key innovation of Bitcoin is how transactions are recorded in the distributed database through mining. Transactions are grouped into blocks and about every 10 minutes a new block of transactions is sent out, becoming part of the transaction log known as the blockchain, which indicates the transaction has been made (more-or-less) official.[6] Bitcoin mining is the process that puts transactions into a block, to make sure everyone has a consistent view of the transaction log. To mine a block, miners must find an extremely rare solution to an (otherwise-pointless) cryptographic problem. Finding this solution generates a mined block, which becomes part of the official block chain.
Mining is also the mechanism for new bitcoins to enter the system. When a block is successfully mined, new bitcoins are generated in the block and paid to the miner. This mining bounty is large - currently 25 bitcoins per block (about $19,000). In addition, the miner gets any fees associated with the transactions in the block. Because of this, mining is very competitive with many people attempting to mine blocks. The difficulty and competitiveness of mining is a key part of Bitcoin security, since it ensures that nobody can flood the system with bad blocks.
The peer-to-peer network
There is no centralized Bitcoin server. Instead, Bitcoin runs on a peer-to-peer network. If you run a Bitcoin client, you become part of that network. The nodes on the network exchange transactions, blocks, and addresses of other peers with each other. When you first connect to the network, your client downloads the blockchain from some random node or nodes. In turn, your client may provide data to other nodes. When you create a Bitcoin transaction, you send it to some peer, who sends it to other peers, and so on, until it reaches the entire network. Miners pick up your transaction, generate a mined block containing your transaction, and send this mined block to peers. Eventually your client will receive the block and your client shows that the transaction was processed.Cryptography
Bitcoin uses digital signatures to ensure that only the owner of bitcoins can spend them. The owner of a Bitcoin address has the private key associated with the address. To spend bitcoins, they sign the transaction with this private key, which proves they are the owner. (It's somewhat like signing a physical check to make it valid.) A public key is associated with each Bitcoin address, and anyone can use it to verify the digital signature.Blocks and transactions are identified by a 256-bit cryptographic hash of their contents. This hash value is used in multiple places in the Bitcoin protocol. In addition, finding a special hash is the difficult task in mining a block.
Diving into the raw Bitcoin protocol
The remainder of this article discusses, step by step, how I used the raw Bitcoin protocol. First I generated a Bitcoin address and keys. Next I made a transaction to move a small amount of bitcoins to this address. Signing this transaction took me a lot of time and difficulty. Finally, I fed this transaction into the Bitcoin peer-to-peer network and waited for it to get mined. The remainder of this article describes these steps in detail.It turns out that actually using the Bitcoin protocol is harder than I expected. As you will see, the protocol is a bit of a jumble: it uses big-endian numbers, little-endian numbers, fixed-length numbers, variable-length numbers, custom encodings, DER encoding, and a variety of cryptographic algorithms, seemingly arbitrarily. As a result, there's a lot of annoying manipulation to get data into the right format.[7]
The second complication with using the protocol directly is that being cryptographic, it is very unforgiving. If you get one byte wrong, the transaction is rejected with no clue as to where the problem is.[8]
The final difficulty I encountered is that the process of signing a transaction is much more difficult than necessary, with a lot of details that need to be correct. In particular, the version of a transaction that gets signed is very different from the version that actually gets used.
Bitcoin addresses and keys
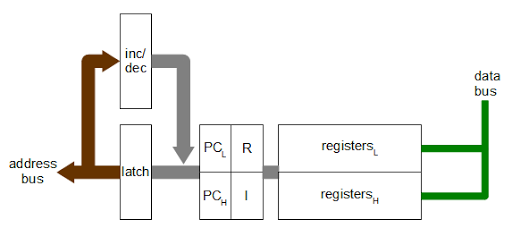
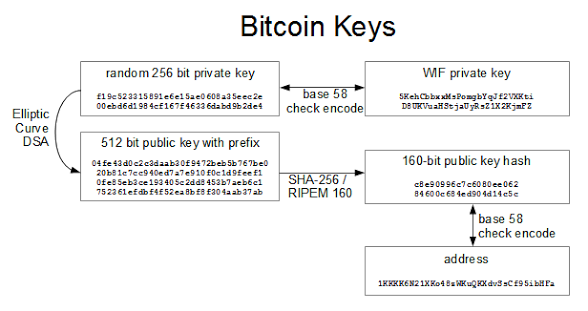
My first step was to create a Bitcoin address. Normally you use Bitcoin client software to create an address and the associated keys. However, I wrote some Python code to create the address, showing exactly what goes on behind the scenes.Bitcoin uses a variety of keys and addresses, so the following diagram may help explain them. You start by creating a random 256-bit private key. The private key is needed to sign a transaction and thus transfer (spend) bitcoins. Thus, the private key must be kept secret or else your bitcoins can be stolen.
The Elliptic Curve DSA algorithm generates a 512-bit public key from the private key. (Elliptic curve cryptography will be discussed later.) This public key is used to verify the signature on a transaction. Inconveniently, the Bitcoin protocol adds a prefix of 04 to the public key. The public key is not revealed until a transaction is signed, unlike most systems where the public key is made public.
The next step is to generate the Bitcoin address that is shared with others.
Since the 512-bit public key is inconveniently large, it is hashed down to 160 bits using the SHA-256 and RIPEMD hash algorithms.[9] The key is then encoded in ASCII using Bitcoin's custom Base58Check encoding.[10] The resulting address, such as 1KKKK6N21XKo48zWKuQKXdvSsCf95ibHFa, is the address people publish in order to receive bitcoins. Note that you cannot determine the public key or the private key from the address. If you lose your private key (for instance by throwing out your hard drive), your bitcoins are lost forever.
Finally, the Wallet Interchange Format key (WIF) is used to add a private key to your client wallet software. This is simply a Base58Check encoding of the private key into ASCII, which is easily reversed to obtain the 256-bit private key. (I was curious if anyone would use the private key above to steal my 80 cents of bitcoins, and sure enough someone did.)
To summarize, there are three types of keys: the private key, the public key, and the hash of the public key, and they are represented externally in ASCII using Base58Check encoding. The private key is the important key, since it is required to access the bitcoins and the other keys can be generated from it. The public key hash is the Bitcoin address you see published.
I used the following code snippet[11] to generate a private key in WIF format and an address. The private key is simply a random 256-bit number. The ECDSA crypto library generates the public key from the private key.[12] The Bitcoin address is generated by SHA-256 hashing, RIPEMD-160 hashing, and then Base58 encoding with checksum. Finally, the private key is encoded in Base58Check to generate the WIF encoding used to enter a private key into Bitcoin client software.[1] Note: this Python random function is not cryptographically strong; use a better function if you're doing this for real.
Inside a transaction
A transaction is the basic operation in the Bitcoin system. You might expect that a transaction simply moves some bitcoins from one address to another address, but it's more complicated than that. A Bitcoin transaction moves bitcoins between one or more inputs and outputs. Each input is a transaction and address supplying bitcoins. Each output is an address receiving bitcoin, along with the amount of bitcoins going to that address.
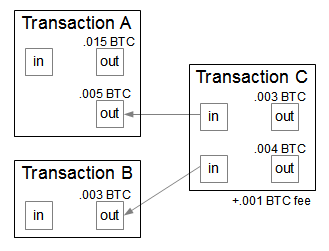
The diagram above shows a sample transaction "C". In this transaction, .005 BTC are taken from an address in Transaction A, and .003 BTC are taken from an address in Transaction B. (Note that arrows are references to the previous outputs, so are backwards to the flow of bitcoins.) For the outputs, .003 BTC are directed to the first address and .004 BTC are directed to the second address. The leftover .001 BTC goes to the miner of the block as a fee. Note that the .015 BTC in the other output of Transaction A is not spent in this transaction.
Each input used must be entirely spent in a transaction. If an address received 100 bitcoins in a transaction and you just want to spend 1 bitcoin, the transaction must spend all 100. The solution is to use a second output for change, which returns the 99 leftover bitcoins back to you.
Transactions can also include fees. If there are any bitcoins left over after adding up the inputs and subtracting the outputs, the remainder is a fee paid to the miner. The fee isn't strictly required, but transactions without a fee will be a low priority for miners and may not be processed for days or may be discarded entirely.[13] A typical fee for a transaction is 0.0002 bitcoins (about 20 cents), so fees are low but not trivial.
Manually creating a transaction
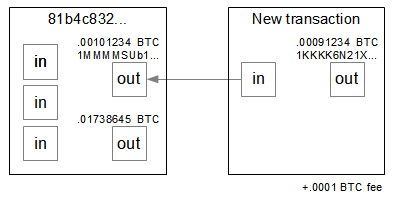
For my experiment I used a simple transaction with one input and one output, which is shown below. I started by buying bitcoins from Coinbase and putting 0.00101234 bitcoins into address1MMMMSUb1piy2ufrSguNUdFmAcvqrQF8M5, which was transaction 81b4c832.... My goal was to create a transaction to transfer these bitcoins to the address I created above,
1KKKK6N21XKo48zWKuQKXdvSsCf95ibHFa, subtracting a fee of 0.0001 bitcoins. Thus, the destination address will receive 0.00091234 bitcoins.
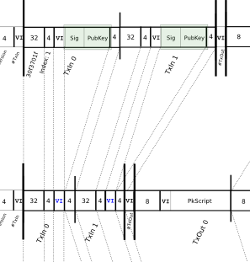
Following the specification, the unsigned transaction can be assembled fairly easily, as shown below. There is one input, which is using output 0 (the first output) from transaction 81b4c832.... Note that this transaction hash is inconveniently reversed in the transaction. The output amount is 0.00091234 bitcoins (91234 is 0x016462 in hex), which is stored in the value field in little-endian form. The cryptographic parts - scriptSig and scriptPubKey - are more complex and will be discussed later.
| version | 01 00 00 00 | |
| input count | 01 | |
| input | previous output hash (reversed) | 48 4d 40 d4 5b 9e a0 d6 52 fc a8 25 8a b7 ca a4 25 41 eb 52 97 58 57 f9 6f b5 0c d7 32 c8 b4 81 |
| previous output index | 00 00 00 00 | |
| script length | ||
| scriptSig | script containing signature | |
| sequence | ff ff ff ff | |
| output count | 01 | |
| output | value | 62 64 01 00 00 00 00 00 |
| script length | ||
| scriptPubKey | script containing destination address | |
| block lock time | 00 00 00 00 | |
Here's the code I used to generate this unsigned transaction. It's just a matter of packing the data into binary. Signing the transaction is the hard part, as you'll see next.
How Bitcoin transactions are signed
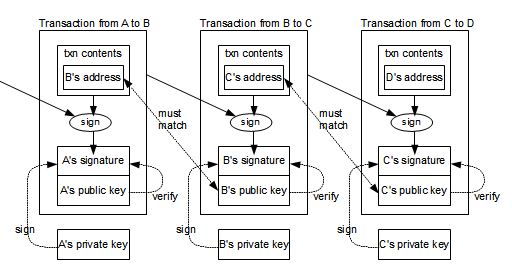
The following diagram gives a simplified view of how transactions are signed and linked together.[14] Consider the middle transaction, transferring bitcoins from address B to address C. The contents of the transaction (including the hash of the previous transaction) are hashed and signed with B's private key. In addition, B's public key is included in the transaction.By performing several steps, anyone can verify that the transaction is authorized by B. First, B's public key must correspond to B's address in the previous transaction, proving the public key is valid. (The address can easily be derived from the public key, as explained earlier.) Next, B's signature of the transaction can be verified using the B's public key in the transaction. These steps ensure that the transaction is valid and authorized by B. One unexpected part of Bitcoin is that B's public key isn't made public until it is used in a transaction.
With this system, bitcoins are passed from address to address through a chain of transactions. Each step in the chain can be verified to ensure that bitcoins are being spent validly. Note that transactions can have multiple inputs and outputs in general, so the chain branches out into a tree.
The Bitcoin scripting language
You might expect that a Bitcoin transaction is signed simply by including the signature in the transaction, but the process is much more complicated. In fact, there is a small program inside each transaction that gets executed to decide if a transaction is valid. This program is written in Script, the stack-based Bitcoin scripting language. Complex redemption conditions can be expressed in this language. For instance, an escrow system can require two out of three specific users must sign the transaction to spend it. Or various types of contracts can be set up.[15]The Script language is surprisingly complex, with about 80 different opcodes. It includes arithmetic, bitwise operations, string operations, conditionals, and stack manipulation. The language also includes the necessary cryptographic operations (SHA-256, RIPEMD, etc.) as primitives. In order to ensure that scripts terminate, the language does not contain any looping operations. (As a consequence, it is not Turing-complete.) In practice, however, only a few types of transactions are supported.[16]
In order for a Bitcoin transaction to be valid, the two parts of the redemption script must run successfully. The script in the old transaction is called scriptPubKey and the script in the new transaction is called scriptSig. To verify a transaction, the scriptSig executed followed by the scriptPubKey. If the script completes successfully, the transaction is valid and the Bitcoin can be spent. Otherwise, the transaction is invalid. The point of this is that the scriptPubKey in the old transaction defines the conditions for spending the bitcoins. The scriptSig in the new transaction must provide the data to satisfy the conditions.
In a standard transaction, the scriptSig pushes the signature (generated from the private key) to the stack, followed by the public key. Next, the scriptPubKey (from the source transaction) is executed to verify the public key and then verify the signature.
As expressed in Script, the scriptSig is:
PUSHDATA signature data and SIGHASH_ALL PUSHDATA public key dataThe scriptPubKey is:
OP_DUP OP_HASH160 PUSHDATA Bitcoin address (public key hash) OP_EQUALVERIFY OP_CHECKSIG
When this code executes, PUSHDATA first pushes the signature to the stack. The next PUSHDATA pushes the public key to the stack. Next, OP_DUP duplicates the public key on the stack. OP_HASH160 computes the 160-bit hash of the public key. PUSHDATA pushes the required Bitcoin address. Then OP_EQUALVERIFY verifies the top two stack values are equal - that the public key hash from the new transaction matches the address in the old address. This proves that the public key is valid. Next, OP_CHECKSIG checks that the signature of the transaction matches the public key and signature on the stack. This proves that the signature is valid.
Signing the transaction
I found signing the transaction to be the hardest part of using Bitcoin manually, with a process that is surprisingly difficult and error-prone. The basic idea is to use the ECDSA elliptic curve algorithm and the private key to generate a digital signature of the transaction, but the details are tricky. The signing process has been described through a 19-step process (more info). Click the thumbnail below for a detailed diagram of the process.
The biggest complication is the signature appears in the middle of the transaction, which raises the question of how to sign the transaction before you have the signature. To avoid this problem, the scriptPubKey script is copied from the source transaction into the spending transaction (i.e. the transaction that is being signed) before computing the signature. Then the signature is turned into code in the Script language, creating the scriptSig script that is embedded in the transaction. It appears that using the previous transaction's scriptPubKey during signing is for historical reasons rather than any logical reason.[17] For transactions with multiple inputs, signing is even more complicated since each input requires a separate signature, but I won't go into the details.
One step that tripped me up is the hash type. Before signing, the transaction has a hash type constant temporarily appended. For a regular transaction, this is SIGHASH_ALL (0x00000001). After signing, this hash type is removed from the end of the transaction and appended to the scriptSig.
Another annoying thing about the Bitcoin protocol is that the signature and public key are both 512-bit elliptic curve values, but they are represented in totally different ways: the signature is encoded with DER encoding but the public key is represented as plain bytes. In addition, both values have an extra byte, but positioned inconsistently: SIGHASH_ALL is put after the signature, and type 04 is put before the public key.
Debugging the signature was made more difficult because the ECDSA algorithm uses a random number.[18] Thus, the signature is different every time you compute it, so it can't be compared with a known-good signature.
Update (Feb 2014): An important side-effect of the signature changing every time is that if you re-sign a transaction, the transaction's hash will change. This is known as Transaction Malleability. There are also ways that third parties can modify transactions in trivial ways that change the hash but not the meaning of the transaction. Although it has been known for years, malleability has recently caused big problems (Feb 2014) with MtGox (press release).
With these complications it took me a long time to get the signature to work. Eventually, though, I got all the bugs out of my signing code and succesfully signed a transaction. Here's the code snippet I used.
The final scriptSig contains the signature along with the public key for the source address (1MMMMSUb1piy2ufrSguNUdFmAcvqrQF8M5). This proves I am allowed to spend these bitcoins, making the transaction valid.
| PUSHDATA 47 | 47 | |
| signature (DER) |
sequence | 30 |
| length | 44 | |
| integer | 02 | |
| length | 20 | |
| X | 2c b2 65 bf 10 70 7b f4 93 46 c3 51 5d d3 d1 6f c4 54 61 8c 58 ec 0a 0f f4 48 a6 76 c5 4f f7 13 | |
| integer | 02 | |
| length | 20 | |
| Y | 6c 66 24 d7 62 a1 fc ef 46 18 28 4e ad 8f 08 67 8a c0 5b 13 c8 42 35 f1 65 4e 6a d1 68 23 3e 82 | |
| SIGHASH_ALL | 01 | |
| PUSHDATA 41 | 41 | |
| public key | type | 04 |
| X | 14 e3 01 b2 32 8f 17 44 2c 0b 83 10 d7 87 bf 3d 8a 40 4c fb d0 70 4f 13 5b 6a d4 b2 d3 ee 75 13 | |
| Y | 10 f9 81 92 6e 53 a6 e8 c3 9b d7 d3 fe fd 57 6c 54 3c ce 49 3c ba c0 63 88 f2 65 1d 1a ac bf cd | |
The final scriptPubKey contains the script that must succeed to spend the bitcoins. Note that this script is executed at some arbitrary time in the future when the bitcoins are spent.
It contains the destination address
(1KKKK6N21XKo48zWKuQKXdvSsCf95ibHFa) expressed in hex, not Base58Check. The effect is that only the owner of the private key for this address can spend the bitcoins, so that address is in effect the owner.
| OP_DUP | 76 |
| OP_HASH160 | a9 |
| PUSHDATA 14 | 14 |
| public key hash | c8 e9 09 96 c7 c6 08 0e e0 62 84 60 0c 68 4e d9 04 d1 4c 5c |
| OP_EQUALVERIFY | 88 |
| OP_CHECKSIG | ac |
The final transaction
Once all the necessary methods are in place, the final transaction can be assembled. The final transaction is shown below. This combines the scriptSig and scriptPubKey above with the unsigned transaction described earlier.
| version | 01 00 00 00 | |
| input count | 01 | |
| input | previous output hash (reversed) | 48 4d 40 d4 5b 9e a0 d6 52 fc a8 25 8a b7 ca a4 25 41 eb 52 97 58 57 f9 6f b5 0c d7 32 c8 b4 81 |
| previous output index | 00 00 00 00 | |
| script length | 8a | |
| scriptSig | 47 30 44 02 20 2c b2 65 bf 10 70 7b f4 93 46 c3 51 5d d3 d1 6f c4 54 61 8c 58 ec 0a 0f f4 48 a6 76 c5 4f f7 13 02 20 6c 66 24 d7 62 a1 fc ef 46 18 28 4e ad 8f 08 67 8a c0 5b 13 c8 42 35 f1 65 4e 6a d1 68 23 3e 82 01 41 04 14 e3 01 b2 32 8f 17 44 2c 0b 83 10 d7 87 bf 3d 8a 40 4c fb d0 70 4f 13 5b 6a d4 b2 d3 ee 75 13 10 f9 81 92 6e 53 a6 e8 c3 9b d7 d3 fe fd 57 6c 54 3c ce 49 3c ba c0 63 88 f2 65 1d 1a ac bf cd | |
| sequence | ff ff ff ff | |
| output count | 01 | |
| output | value | 62 64 01 00 00 00 00 00 |
| script length | 19 | |
| scriptPubKey | 76 a9 14 c8 e9 09 96 c7 c6 08 0e e0 62 84 60 0c 68 4e d9 04 d1 4c 5c 88 ac | |
| block lock time | 00 00 00 00 | |
A tangent: understanding elliptic curves
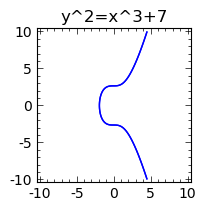
Bitcoin uses elliptic curves as part of the signing algorithm. I had heard about elliptic curves before in the context of solving Fermat's Last Theorem, so I was curious about what they are. The mathematics of elliptic curves is interesting, so I'll take a detour and give a quick overview.The name elliptic curve is confusing: elliptic curves are not ellipses, do not look anything like ellipses, and they have very little to do with ellipses. An elliptic curve is a curve satisfying the fairly simple equation y^2 = x^3 + ax + b. Bitcoin uses a specific elliptic curve called secp256k1 with the simple equation y^2=x^3+7. [25]
An important property of elliptic curves is that you can define addition of points on the curve with a simple rule: if you draw a straight line through the curve and it hits three points A, B, and C, then addition is defined by A+B+C=0. Due to the special nature of elliptic curves, addition defined in this way works "normally" and forms a group. With addition defined, you can define integer multiplication: e.g. 4A = A+A+A+A.
What makes elliptic curves useful cryptographically is that it's fast to do integer multiplication, but division basically requires brute force. For example, you can compute a product such as 12345678*A = Q really quickly (by computing powers of 2), but if you only know A and Q solving n*A = Q is hard. In elliptic curve cryptography, the secret number 12345678 would be the private key and the point Q on the curve would be the public key.
In cryptography, instead of using real-valued points on the curve, the coordinates are integers modulo a prime.[19] One of the surprising properties of elliptic curves is the math works pretty much the same whether you use real numbers or modulo arithmetic. Because of this, Bitcoin's elliptic curve doesn't look like the picture above, but is a random-looking mess of 256-bit points (imagine a big gray square of points).
The Elliptic Curve Digital Signature Algorithm (ECDSA) takes a message hash, and then does some straightforward elliptic curve arithmetic using the message, the private key, and a random number[18] to generate a new point on the curve that gives a signature. Anyone who has the public key, the message, and the signature can do some simple elliptic curve arithmetic to verify that the signature is valid. Thus, only the person with the private key can sign a message, but anyone with the public key can verify the message.
For more on elliptic curves, see the references[20].
Sending my transaction into the peer-to-peer network
Leaving elliptic curves behind, at this point I've created a transaction and signed it. The next step is to send it into the peer-to-peer network, where it will be picked up by miners and incorporated into a block.How to find peers
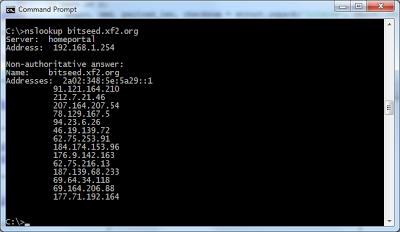
The first step in using the peer-to-peer network is finding a peer. The list of peers changes every few seconds, whenever someone runs a client. Once a node is connected to a peer node, they share new peers by exchanging addr messages whenever a new peer is discovered. Thus, new peers rapidly spread through the system.There's a chicken-and-egg problem, though, of how to find the first peer. Bitcoin clients solve this problem with several methods. Several reliable peers are registered in DNS under the name bitseed.xf2.org. By doing a nslookup, a client gets the IP addresses of these peers, and hopefully one of them will work. If that doesn't work, a seed list of peers is hardcoded into the client. [26]
Peers enter and leave the network when ordinary users start and stop Bitcoin clients, so there is a lot of turnover in clients. The clients I use are unlikely to be operational right now, so you'll need to find new peers if you want to do experiments. You may need to try a bunch to find one that works.
Talking to peers
Once I had the address of a working peer, the next step was to send my transaction into the peer-to-peer network.[8] Using the peer-to-peer protocol is pretty straightforward. I opened a TCP connection to an arbitrary peer on port 8333, started sending messages, and received messages in turn. The Bitcoin peer-to-peer protocol is pretty forgiving; peers would keep communicating even if I totally messed up requests.Important note: as a few people pointed out, if you want to experiment you should use the Bitcoin Testnet, which lets you experiment with "fake" bitcoins, since it's easy to lose your valuable bitcoins if you mess up on the real network. (For example, if you forget the change address in a transaction, excess bitcoins will go to the miners as a fee.) But I figured I would use the real Bitcoin network and risk my $1.00 worth of bitcoins.
The protocol consists of about 24 different message types. Each message is a fairly straightforward binary blob containing an ASCII command name and a binary payload appropriate to the command. The protocol is well-documented on the Bitcoin wiki.
The first step when connecting to a peer is to establish the connection by exchanging version messages. First I send a version message with my protocol version number[21], address, and a few other things. The peer sends its version message back. After this, nodes are supposed to acknowledge the version message with a verack message. (As I mentioned, the protocol is forgiving - everything works fine even if I skip the verack.)
Generating the version message isn't totally trivial since it has a bunch of fields, but it can be created with a few lines of Python. makeMessage below builds an arbitrary peer-to-peer message from the magic number, command name, and payload. getVersionMessage creates the payload for a version message by packing together the various fields.
Sending a transaction: tx
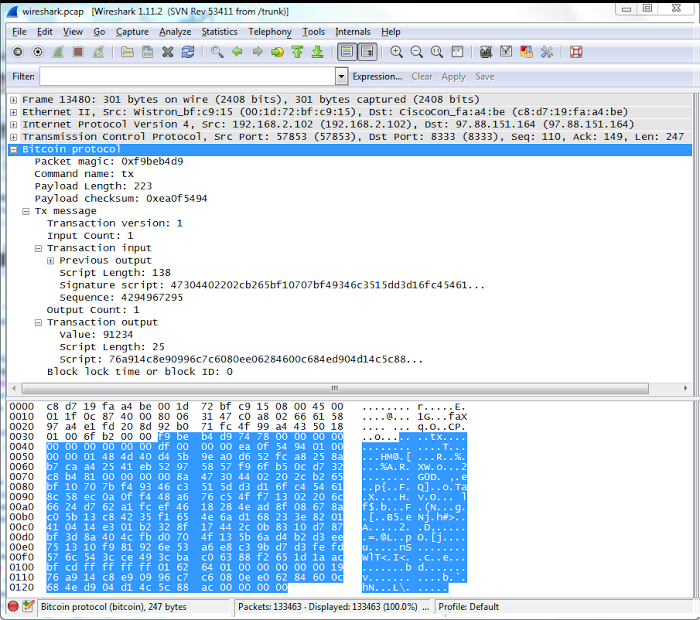
I sent the transaction into the peer-to-peer network with the stripped-down Python script below. The script sends a version message, receives (and ignores) the peer's version and verack messages, and then sends the transaction as a tx message. The hex string is the transaction that I created earlier.The following screenshot shows how sending my transaction appears in the Wireshark network analysis program[22]. I wrote Python scripts to process Bitcoin network traffic, but to keep things simple I'll just use Wireshark here. The "tx" message type is visible in the ASCII dump, followed on the next line by the start of my transaction (01 00 ...).
To monitor the progress of my transaction, I had a socket opened to another random peer. Five seconds after sending my transaction, the other peer sent me a tx message with the hash of the transaction I just sent. Thus, it took just a few seconds for my transaction to get passed around the peer-to-peer network, or at least part of it.
Victory: my transaction is mined
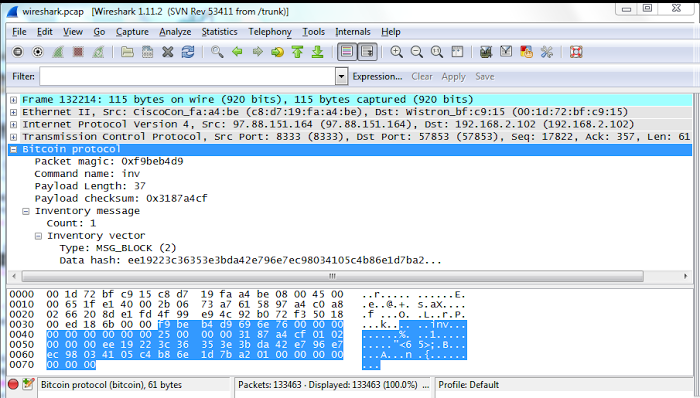
After sending my transaction into the peer-to-peer network, I needed to wait for it to be mined before I could claim victory. Ten minutes later my script received an inv message with a new block (see Wireshark trace below). Checking this block showed that it contained my transaction, proving my transaction worked. I could also verify the success of this transaction by looking in my Bitcoin wallet and by checking online. Thus, after a lot of effort, I had successfully created a transaction manually and had it accepted by the system. (Needless to say, my first few transaction attempts weren't successful - my faulty transactions vanished into the network, never to be seen again.[8])
My transaction was mined by the large GHash.IO mining pool, into block
#279068 with hash 0000000000000001a27b1d6eb8c405410398ece796e742da3b3e35363c2219ee. (The hash is reversed in inv message above: ee19...) Note that the hash starts with a large number of zeros - finding such a literally one in a quintillion value is what makes mining so difficult. This particular block contains 462 transactions, of which my transaction is just one.
For mining this block, the miners received the reward of 25 bitcoins, and total fees of 0.104 bitcoins, approximately $19,000 and $80 respectively. I paid a fee of 0.0001 bitcoins, approximately 8 cents or 10% of my transaction. The mining process is very interesting, but I'll leave that for a future article.
Conclusion
Using the raw Bitcoin protocol turned out to be harder than I expected, but I learned a lot about bitcoins along the way, and I hope you did too. My code is purely for demonstration - if you actually want to use bitcoins through Python, use a real library[24] rather than my code.Notes and references
[1] The original Bitcoin client is Bitcoin-qt. In case you're wondering why qt, the client uses the common Qt UI framework. Alternatively you can use wallet software that doesn't participate in the peer-to-peer network, such as Electrum or MultiBit. Or you can use an online wallet such as Blockchain.info.[2] A couple good articles on Bitcoin are How it works and the very thorough How the Bitcoin protocol actually works.
[3] The original Bitcoin paper is Bitcoin: A Peer-to-Peer Electronic Cash System written by the pseudonymous Satoshi Nakamoto in 2008. The true identity of Satoshi Nakamoto is unknown, although there are many theories.
[4] You may have noticed that sometimes Bitcoin is capitalized and sometimes not. It's not a problem with my shift key - the "official" style is to capitalize Bitcoin when referring to the system, and lower-case bitcoins when referring to the currency units.
[5] In case you're wondering how the popular MtGox Bitcoin exchange got its name, it was originally a trading card exchange called "Magic: The Gathering Online Exchange" and later took the acronym as its name.
[6] For more information on what data is in the blockchain, see the very helpful article Bitcoin, litecoin, dogecoin: How to explore the block chain.
[7] I'm not the only one who finds the Bitcoin transaction format inconvenient. For a rant on how messed up it is, see Criticisms of Bitcoin's raw txn format.
[8] You can also generate transaction and send raw transactions into the Bitcoin network using the bitcoin-qt console. Type sendrawtransaction a1b2c3d4.... This has the advantage of providing information in the debug log if the transaction is rejected. If you just want to experiment with the Bitcoin network, this is much, much easier than my manual approach.
[9] Apparently there's no solid reason to use RIPEMD-160 hashing to create the address and SHA-256 hashing elsewhere, beyond a vague sense that using a different hash algorithm helps security. See discussion. Using one round of SHA-256 is subject to a length extension attack, which explains why double-hashing is used.
[10] The Base58Check algorithm is documented on the Bitcoin wiki. It is similar to base 64 encoding, except it omits the O, 0, I, and l characters to avoid ambiguity in printed text. A 4-byte checksum guards against errors, since using an erroneous bitcoin address will cause the bitcoins to be lost forever.
[11] Some boilerplate has been removed from the code snippets. For the full Python code, see my repository shirriff/bitcoin-code on GitHub. You will also need the ecdsa cryptography library.
[12] You may wonder how I ended up with addresses with nonrandom prefixes such as 1MMMM. The answer is brute force - I ran the address generation script overnight and collected some good addresses. (These addresses made it much easier to recognize my transactions in my testing.) There are scripts and websites that will generate these "vanity" addresses for you.
[13] For a summary of Bitcoin fees, see bitcoinfees.com. This recent Reddit discussion of fees is also interesting.
[14] The original Bitcoin paper has a similar figure showing how transactions are chained together. I find it very confusing though, since it doesn't distinguish between the address and the public key.
[15] For details on the different types of contracts that can be set up with Bitcoin, see Contracts. One interesting type is the 2-of-3 escrow transaction, where two out of three parties must sign the transaction to release the bitcoins. Bitrated is one site that provides these.
[16] Although Bitcoin's Script language is very flexible, the Bitcoin network only permits a few standard transaction types and non-standard transactions are not propagated (details). Some miners will accept non-standard transactions directly, though.
[17] There isn't a security benefit from copying the scriptPubKey into the spending transaction before signing since the hash of the original transaction is included in the spending transaction. For discussion, see Why TxPrev.PkScript is inserted into TxCopy during signature check?
[18] The random number used in the elliptic curve signature algorithm is critical to the security of signing. Sony used a constant instead of a random number in the PlayStation 3, allowing the private key to be determined. In an incident related to Bitcoin, a weakness in the random number generator allowed bitcoins to be stolen from Android clients.
[19] For Bitcoin, the coordinates on the elliptic curve are integers modulo the prime2^256 - 2^32 - 2^9 -2^8 - 2^7 - 2^6 -2^4 -1, which is very nearly 2^256. This is why the keys in Bitcoin are 256-bit keys.
[20] For information on the historical connection between elliptic curves and ellipses (the equation turns up when integrating to compute the arc length of an ellipse) see the interesting article Why Ellipses Are Not Elliptic Curves, Adrian Rice and Ezra Brown, Mathematics Magazine, vol. 85, 2012, pp. 163-176. For more introductory information on elliptic curve cryptography, see ECC tutorial or A (Relatively Easy To Understand) Primer on Elliptic Curve Cryptography. For more on the mathematics of elliptic curves, see An Introduction to the Theory of Elliptic Curves by Joseph H. Silverman. Three Fermat trails to elliptic curves includes a discussion of how Fermat's Last Theorem was solved with elliptic curves.
[21] There doesn't seem to be documentation on the different Bitcoin protocol versions other than the code. I'm using version 60002 somewhat arbitrarily.
[22] The Wireshark network analysis software can dump out most types of Bitcoin packets, but only if you download a recent "beta release - I'm using version 1.11.2.
[24] Several Bitcoin libraries in Python are bitcoin-python, pycoin, and python-bitcoinlib.
[25] The elliptic curve plot was generated from the Sage mathematics package:
var("x y")
implicit_plot(y^2-x^3-7, (x,-10, 10), (y,-10, 10), figsize=3, title="y^2=x^3+7")
[26] The hardcoded peer list in the Bitcoin client is in chainparams.cpp in the array pnseed. For more information on finding Bitcoin peers, see How Bitcoin clients find each other or Satoshi client node discovery.
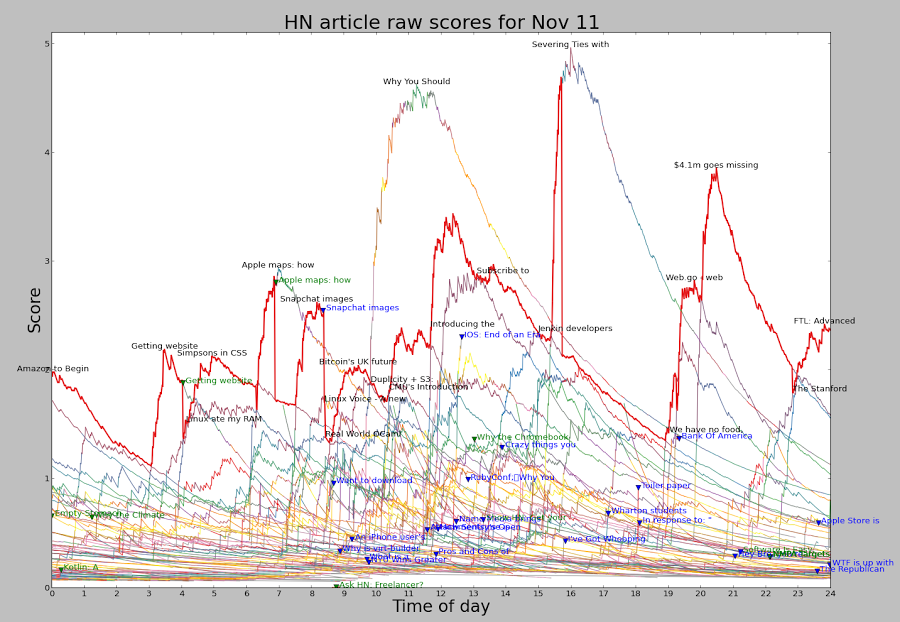
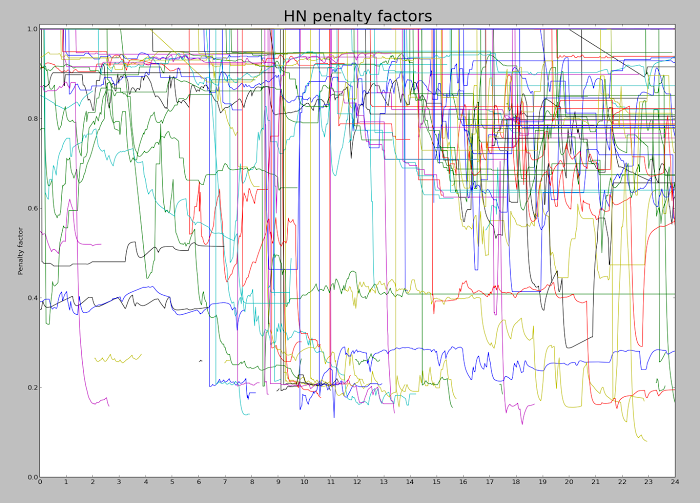
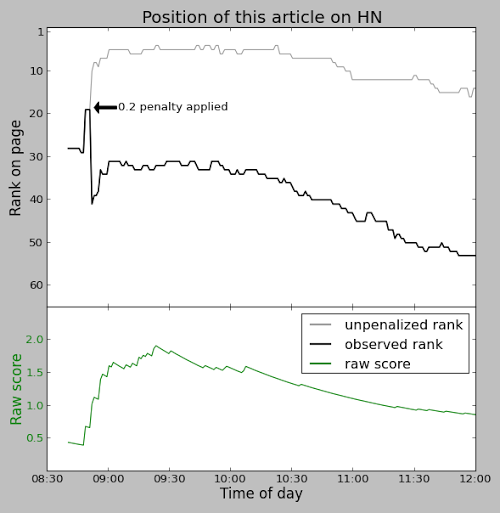
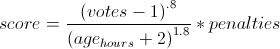Because the time has a larger exponent than the votes, an article's score will eventually drop to zero, so nothing stays on the front page too long. This exponent is known as gravity.
You might expect that every time you visit Hacker News, the stories are scored by the above formula and sorted to determine their rankings. But for efficiency, stories are individually reranked only occasionally. When a story is upvoted, it is reranked and moved up or down the list to its appropriate spot, leaving the other stories unchanged. Thus, the amount of reranking is significantly reduced. There is, however, the possibility that a story stops getting votes and ends up stuck in a high position. To avoid this, every 30 seconds one of the top 50 stories is randomly selected and reranked. The consequence is that a story may be "wrongly" ranked for many minutes if it isn't getting votes.
In addition, pages can be cached for 90 seconds.
![A circuit to increment or decrement two bits at once.](http://static.righto.com/images/z80/incdec4.png" "A circuit to increment or decrement two bits at once.")
