Recently Craig Venter (who decoded the human genome) created a synthetic bacterium. The J. Craig Venter Institute (JCVI) took a bacterium's DNA sequence as a computer file, modified it, made physical DNA from this sequence, and stuck this DNA into a cell, which then reproduced under control of the new DNA to create a new bacterium. This is a really cool result, since it shows you can create the DNA of an organism entirely from scratch. (I wouldn't exactly call it synthetic life though, since it does require an existing cell to get going.) Although this project took 10 years to complete, I'm sure it's only a matter of time before you will be able to send a data file to some company and get the resulting cells sent back to you.
One interesting feature of this synthetic bacterium is it includes four "watermarks", special sequences of DNA that prove this bacterium was created from the data file, and is not natural. However, they didn't reveal how the watermarks were encoded. The DNA sequences were published (GTTCGAATATTT and so on), but how to get the meaning out of this was left a puzzle. For detailed background on the watermarks, see Singularity Hub. I broke the code (as I described earlier) and found the names of the authors, some quotations, and the following hidden web page. This seems like science fiction, but it's true. There's actually a new bacterium that has a web page encoded in its DNA:
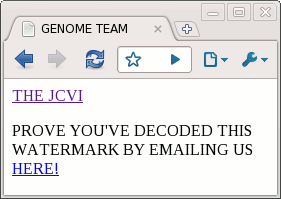
I contacted the JCVI using the link and found out I was the 31st person to break the code, which is a bit disappointing. I haven't seen details elsewhere on how the code works, so I'll provide the details. (Spoilers ahead if you want to break the code yourself.) I originally used Python to break the code, but since this is nominally an Arc blog, I'll show how it can be done using the Arc language.
The oversimplified introduction to DNA
Perhaps I should give the crash course in DNA at this point. The genetic instructions for all organisms are contained in very, very long molecules called DNA. For our purposes, DNA can be described as a sequence of four different letters: C, G, A, and T. The human genome is 3 billion base pairs in 23 chromosome pairs, so your DNA can be described as a pair of sequences of 3 billion C's, G's, A's, and T's.
Watson and Crick won the Nobel Prize for figuring out the structure of DNA and how it encodes genes. Your body is made up of important things such as enzymes, which are made up of carefully-constructed proteins, which are made up of special sequences of 18 different amino acids. Your genes, which are parts of the DNA, specify these amino acid sequences. Each three DNA bases specify a particular amino acid in the sequence. For instance, the DNA sequence CTATGG specifies the amino acids leucine and tryptophan because CTA indicates leucine, and TGG indicates tryptophan. Crick and Watson and Rosalind Franklin discovered the genetic code that associates a particular amino acid with each of the 64 possible DNA triples. I'm omitting lots of interesting details here, but the key point is that each three DNA symbols specifies one amino acid.
Encoding text in DNA
Now, the puzzle is to figure out how JCVI encoded text in the synthetic bacterium's DNA. The obvious extension is instead of assigning an amino acid to each of the 64 DNA triples, assign a character to it. (I should admit that this was only obvious to me in retrospect, as I explained in my earlier blog posting.) Thus if the DNA sequence is GTTCGA, then GTT will be one letter and CGA will be another, and so on. Now we just need to figure out what letter goes with each DNA triple.If we know some text and the DNA that goes with it, it is straightforward to crack the code that maps between the characters and the DNA triples. For instance, if we happen to know that the text "LIFE" corresponds to the DNA "AAC CTG GGC TAA", then we can conclude that AAA goes to L, CTG goes to I, GGC goes to F, and TAA goes to E. But how do we get started?
Conveniently, the Singularity Hub article gives the quotes that appear in the DNA, as reported by JCVI:
"TO LIVE, TO ERR, TO FALL, TO TRIUMPH, TO RECREATE LIFE OUT OF LIFE." "SEE THINGS NOT AS THEY ARE, BUT AS THEY MIGHT BE." "WHAT I CANNOT BUILD, I CANNOT UNDERSTAND."We can try matching the quotes against each position in the DNA and see if there is any position that works. A match can fail in two ways. First, if the same DNA triple corresponds to two different letters, something must be wrong. For instance, if we try to match "LIFE" against "AAC CTG GGC AAC", we would conclude that AAC means both L and E. Second, if the same letter corresponds to two DNA triples, we can reject it. For instance, if we try to match "ERR" against "TAA CTA GTC", then both CTA and GTC would mean R. (Interestingly, the real genetic code has this second type of ambiguity. Because there are only 18 amino acids and 64 DNA triples, many DNA triples indicate the same amino acid.)
Using Arc to break the code
To break the code, first download the DNA sequences of the four watermarks and assign them to variables w1, w2, w3, w4. (Download full code here.)(= w1 "GTTCGAATATTTCTATAGCTGTACA...") (= w2 "CAACTGGCAGCATAAAACATATAGA...") (= w3 "TTTAACCATATTTAAATATCATCCT...") (= w4 "TTTCATTGCTGATCACTGTAGATAT...")Next, lets break the four watermarks into triples by first converting to a list and then taking triples of length 3, which we call t1 through t4:
(def strtolist (s) (accum accfn (each x s (accfn (string x))))) (def tripleize (s) (map string (tuples (strtolist s) 3))) (= t1 (tripleize w1)) (= t2 (tripleize w2)) (= t3 (tripleize w3)) (= t4 (tripleize w4))The next function is the most important. It takes triples and text, matches the triples against the text, and generates a table that maps from each triple to the corresponding characters. If it runs into a problem (either two characters assigned to the same triple, or the same character assigned to two triples) then it fails. Otherwise it returns the code table. It uses tail recursion to scan through the triples and input text together.
; Match the characters in text against the triples.
; codetable is a table mapping triples to characters.
; offset is the offset into text
; Return codetable or nil if no match.
(def matchtext (triples text (o codetable (table)) (o offset 0))
(if (>= offset (len text)) codetable ; success
(with (trip (car triples) ch (text offset))
; if ch is assigned to something else in the table
; then not a match
(if (and (mem ch (vals codetable))
(isnt (codetable trip) ch))
nil
(empty (codetable trip))
(do (= (codetable trip) ch) ; new char
(matchtext (cdr triples) text codetable (+ 1 offset)))
(isnt (codetable trip) ch)
nil ; mismatch
(matchtext (cdr triples) text codetable (+ 1 offset))))))
Finally, the function findtext finds a match anywhere in the triple list. In other words, the previous function matchtext assumes the start of the triples corresponds to the start of the text. But findtext tries to find a match at any point in the triples. It calls matchtext, and if there's no match then it drops the first triple (using cdr) and calls itself recursively, until it runs out of triples.
(def findtext (triples text)
(if (< (len triples) (len text)) nil
(let result (matchtext triples text)
(if result result
(findtext (cdr triples) text)))))
The Singularity Hub article said that the DNA contains the quote:
"TO LIVE, TO ERR, TO FALL, TO TRIUMPH, TO RECREATE LIFE OUT OF LIFE." - JAMES JOYCELet's start by just looking for "LIFE OUT OF LIFE", since we're unlikely to get LIFE to match twice just by chance:
arc> (findtext t1 "LIFE OUT OF LIFE") nilNo match in the first watermark, so let's try the second.
arc> (findtext t2 "LIFE OUT OF LIFE")
#hash(("CGT" . #\O) ("TGA" . #\T) ("CTG" . #\I) ("ATA" . #\space) ("TAA" . #\E) ("AAC" . #\L) ("TCC" . #\U) ("GGC" . #\F))
How about that! Looks like a match in watermark 2, with DNA "AAC" corresponding to L, "CGT" corresponding to "I", "GGC" corresponding to "F", and so on. (The Arc format for hash tables is pretty ugly, but hopefully you can see that in the output.) Let's try matching the full quote and store the table in code2:
arc> (= code2 (findtext t2 "TO LIVE, TO ERR, TO FALL, TO TRIUMPH, TO RECREATE LIFE OUT OF LIFE."))
#hash(("TCC" . #\U) ("TCA" . #\H) ("TTG" . #\V) ("CTG" . #\I) ("ACA" . #\P) ("CTA" . #\R) ("CGA" . #\.) ("ATA" . #\space) ("CGT" . #\O) ("TTT" . #\C) ("TGA" . #\T) ("TAA" . #\E) ("AAC" . #\L) ("CAA" . #\M) ("GTG" . #\,) ("TAG" . #\A) ("GGC" . #\F))
Likewise, we can try matching the other quotes:
arc> (= code3 (findtext t3 "SEE THINGS NOT AS THEY ARE, BUT AS THEY MIGHT BE."))
#hash(("CTA" . #\R) ("TCA" . #\H) ("CTG" . #\I) ("GCT" . #\S) ("CGA" . #\.) ("ATA" . #\space) ("CAT" . #\Y) ("CGT" . #\O) ("TCC" . #\U) ("AGT" . #\B) ("TGA" . #\T) ("TAA" . #\E) ("TGC" . #\N) ("TAC" . #\G) ("CAA" . #\M) ("GTG" . #\,) ("TAG" . #\A))
arc> (= code4 (findtext t4 "WHAT I CANNOT BUILD, I CANNOT UNDERSTAND"))
#hash(("TCC" . #\U) ("TCA" . #\H) ("ATT" . #\D) ("CTG" . #\I) ("GCT" . #\S) ("TTT" . #\C) ("ATA" . #\space) ("TAA" . #\E) ("CGT" . #\O) ("CTA" . #\R) ("TGA" . #\T) ("AGT" . #\B) ("AAC" . #\L) ("TGC" . #\N) ("GTG" . #\,) ("TAG" . #\A) ("GTC" . #\W))
Happily, they all decode the same triples to the same letters, or else we would have a problem. We can merge these three decode tables into one:
arc> (= code (listtab (join (tablist code2) (tablist code3) (tablist code4))))#hash(("TCC" . #\U) ("TCA" . #\H) ("CTA" . #\R) ("CGT" . #\O) ("TGA" . #\T) ("CGA" . #\.) ("TAA" . #\E) ("AAC" . #\L) ("TAC" . #\G) ("TAG" . #\A) ("GGC" . #\F) ("ACA" . #\P) ("ATT" . #\D) ("TTG" . #\V) ("CTG" . #\I) ("GCT" . #\S) ("TTT" . #\C) ("CAT" . #\Y) ("ATA" . #\space) ("AGT" . #\B) ("GTG" . #\,) ("TGC" . #\N) ("CAA" . #\M) ("GTC" . #\W))
Now, let's make a decode function that will apply the string to the unknown DNA and see what we get. (We'll leave unknown triples unconverted.)
(def decode (decodemap triples)
(string (accum accfn (each triple triples (accfn
(if (decodemap triple)
(decodemap triple)
(string "(" triple ")" )))))))
arc> (decode code t1)
"(GTT). CRAIG VENTER INSTITUTE (ACT)(TCT)(TCT)(GTA)(GGG)ABCDEFGHI(GTT)(GCA)LMNOP(TTA)RSTUVW(GGT)Y(TGG)(GGG) (TCT)(CTT)(ACT)(AAT)(AGA)(GCG)(GCC)(TAT)(CGC)(GTA)(TTC)(TCG)(CCG)(GAC)(CCC)(CCT)(CTC)(CCA)(CAC)(CAG)(CGG)(TGT)(AGC)(ATC)(ACC)(AAG)(AAA)(ATG)(AGG)(GGA)(ACG)(GAT)(GAG)(GAA).,(GGG)SYNTHETIC GENOMICS, INC.(GGG)(CGG)(GAG)DOCTYPE HTML(AGC)(CGG)HTML(AGC)(CGG)HEAD(AGC)(CGG)TITLE(AGC)GENOME TEAM(CGG)(CAC)TITLE(AGC)(CGG)(CAC)HEAD(AGC)(CGG)BODY(AGC)(CGG)A HREF(CCA)(GGA)HTTP(CAG)(CAC)(CAC)WWW.(GTT)CVI.ORG(CAC)(GGA)(AGC)THE (GTT)CVI(CGG)(CAC)A(AGC)(CGG)P(AGC)PROVE YOU(GAA)VE DECODED THIS WATERMAR(GCA) BY EMAILING US (CGG)A HREF(CCA)(GGA)MAILTO(CAG)MRO(TTA)STI(TGG)(TCG)(GTT)CVI.ORG(GGA)(AGC)HERE(GAG)(CGG)(CAC)A(AGC)(CGG)(CAC)P(AGC)(CGG)(CAC)BODY(AGC)(CGG)(CAC)HTML(AGC)"
It looks like we're doing pretty well with the decoding, as there's a lot of recognizable text and some HTML in there. There's also conveniently the entire alphabet as a decoding aid. From this, we can fill in a lot of the gaps, e.g. GTT is J and GCA is K. From the HTML tags we can figure out angle brackets, quotes, and slash. We can guess that there are numbers in there and figure out that ACT TCT TCT GTA is 2009. These deductions can be added manually to the decode table:
arc> (= (code "GTT") #\J) arc> (= (code "GCA") #\K) arc> (= (code "ACT") #\2) ...After a couple cycles of adding missing characters and looking at the decodings, we get the almost-complete decodings of the four watermarks:
The contents of the watermarks
J. CRAIG VENTER INSTITUTE 2009
ABCDEFGHIJKLMNOPQRSTUVWXYZ 0123456789(TTC)@(CCG)(GAC)-(CCT)(CTC)=/:<(TGT)>(ATC)(ACC)(AAG)(AAA)(ATG)(AGG)"(ACG)(GAT)!'.,
SYNTHETIC GENOMICS, INC.
<!DOCTYPE HTML><HTML><HEAD><TITLE>GENOME TEAM</TITLE></HEAD><BODY><A HREF="HTTP://WWW.JCVI.ORG/">THE JCVI</A><P>PROVE YOU'VE DECODED THIS WATERMARK BY EMAILING US <A HREF="MAILTO:[email protected]">HERE!</A></P></BODY></HTML>MIKKEL ALGIRE, MICHAEL MONTAGUE, SANJAY VASHEE, CAROLE LARTIGUE, CHUCK MERRYMAN, NINA ALPEROVICH, NACYRA ASSAD-GARCIA, GWYN BENDERS, RAY-YUAN CHUANG, EVGENIA DENISOVA, DANIEL GIBSON, JOHN GLASS, ZHI-QING QI.
"TO LIVE, TO ERR, TO FALL, TO TRIUMPH, TO RECREATE LIFE OUT OF LIFE." - JAMES JOYCECLYDE HUTCHISON, ADRIANA JIGA, RADHA KRISHNAKUMAR, JAN MOY, MONZIA MOODIE, MARVIN FRAZIER, HOLLY BADEN-TILSON, JASON MITCHELL, DANA BUSAM, JUSTIN JOHNSON, LAKSHMI DEVI VISWANATHAN, JESSICA HOSTETLER, ROBERT FRIEDMAN, VLADIMIR NOSKOV, JAYSHREE ZAVERI.
"SEE THINGS NOT AS THEY ARE, BUT AS THEY MIGHT BE."CYNTHIA ANDREWS-PFANNKOCH, QUANG PHAN, LI MA, HAMILTON SMITH, ADI RAMON, CHRISTIAN TAGWERKER, J CRAIG VENTER, EULA WILTURNER, LEI YOUNG, SHIBU YOOSEPH, PRABHA IYER, TIM STOCKWELL, DIANA RADUNE, BRIDGET SZCZYPINSKI, SCOTT DURKIN, NADIA FEDOROVA, JAVIER QUINONES, HANNA TEKLEAB.
"WHAT I CANNOT BUILD, I CANNOT UNDERSTAND." - RICHARD FEYNMAN
The first watermark consists of a copyright-like statement, a list of all the characters, and the hidden HTML page (which I showed above.) The second, third, and fourth watermarks consist of a list of the authors and three quotations.
Note that there are 14 undecoded triples that only appear once in the list of characters. They aren't in ASCII order, keyboard order, or any other order I can figure out, so I can't determine what they are, but I assume they are missing punctuation and special characters.
The DNA decoding table
The following table summarizes the 'secret' DNA to character code:| AAA ? | AAC L | AAG ? | AAT 3 |
| ACA P | ACC ? | ACG ? | ACT 2 |
| AGA 4 | AGC > | AGG ? | AGT B |
| ATA space | ATC ? | ATG ? | ATT D |
| CAA M | CAC / | CAG : | CAT Y |
| CCA = | CCC - | CCG ? | CCT ? |
| CGA . | CGC 8 | CGG < | CGT O |
| CTA R | CTC ? | CTG I | CTT 1 |
| GAA ' | GAC ? | GAG ! | GAT ? |
| GCA K | GCC 6 | GCG 5 | GCT S |
| GGA " | GGC F | GGG newline | GGT X |
| GTA 9 | GTC W | GTG , | GTT J |
| TAA E | TAC G | TAG A | TAT 7 |
| TCA H | TCC U | TCG @ | TCT 0 |
| TGA T | TGC N | TGG Z | TGT ? |
| TTA Q | TTC ? | TTG V | TTT C |
More on breaking the code
It was convenient that the JCVI said in advance what quotations were in the DNA, making it easier to break the code. But could the code still be broken if they hadn't?One way to break the code is to look at statistics of how often different triples appear. We count the triples, convert the table to a list, and then sort the list. In the sort we use a special comparison function that compares the counts, to sort on the counts, not on the triples.
arc> (sort
(fn ((k1 v1) (k2 v2)) (> v1 v2))
(tablist (counts t2)))
(("ATA" 41) ("TAG" 27) ("TAA" 25) ("CTG" 18) ("TGC" 16) ("GTG" 16) ("CTA" 15) ("CGT" 14) ("AAC" 13) ("TGA" 10) ("TTT" 10) ("GCT" 10) ("TAC" 10) ("TCA" 8) ("CAA" 7) ("CAT" 7) ("TCC" 7) ("TTG" 5) ("GGC" 4) ("GTT" 4) ("ATT" 4) ("CCC" 4) ("GCA" 3) ("AGT" 2) ("TTA" 2) ("ACA" 2) ("CGA" 2) ("GGA" 2) ("GTC" 1) ("TGG" 1) ("GGG" 1))
This tells us that ATA appears 41 times in the second watermark, TAG 27 times, and so on. If we assume that this encodes English text, then the most common characters will be space, E, T, A, O, and so on. Then it's a matter of trial-and-error trying the high-frequency letters for the high-frequency triples until we find a combination that yields real words. (It's just like solving a newspaper cryptogram.) You'll notice that the high-frequency triples do turn out to match high-frequency letters, but not in the exact order. (I've written before on simple cryptanalysis with Arc.)
Another possible method is to guess that a phrase such as "CRAIG VENTER" appears in the solution, and try to match that against the triples. This turns out to be the case. It doesn't give a lot of letters to work on, but it's a start.
Arc: still bad for exploratory programming
A couple years ago I wrote that Arc is bad for exploratory programming, which turned out to be hugely controversial. I did this DNA exploration using both Python and Arc, and found Python to be much better for most of the reasons I described in my earlier article.- Libraries: Matching DNA triples was trivial in Python because I could use regular expressions. Arc doesn't have regular expressions (unless you use a nonstandard variant such as Anarki). Another issue was when I wanted to do graphical display of watermark contents; Arc has no graphics support.
- Performance: for the sorts of exploratory programming I do, performance is important. For instance, one thing I did when trying to figure out the code was match all substrings of one watermark against another, to see if there were commonalities. This is O(N^3) and was tolerably fast in Python, but Arc would be too painful.
- Ease of and speed of programming. A lot of the programming speed benefit is that I have more familiarity with Python, but while programming in Arc I would constantly get derailed by cryptic error messages, or trying to figure out how to do simple things like breaking a string into triples. It doesn't help that most of the Arc documentation I wrote myself.
Thoughts on the DNA coding technique
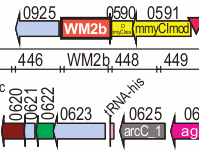I see some potential ways that the DNA coding technique could be improved and extended. Since the the full details of the DNA coding technique haven't been published by the JCVI yet, they may have already considered these ideas.
Being able to embed text in the DNA of a living organism is extremely cool. However, I'm not sure how practical it is. The data density in DNA is very high, maybe 500 times that of a hard drive (ref), but most of the DNA is devoted to keeping the bacterium alive and only about 1K of text is stored in the watermarks.
I received email from JCVI that said the coding mechanism also supports Java, math (LaTeX?), and Perl as well as HTML. Embedding Perl code in a living organism seems even more crazy than text or HTML.
If encoding text in DNA catches on, I'd expect that error correction would be necessary to handle mutations. An error-correction code like Reed-Solomon won't really work because DNA can suffer deletions and insertions as well as mutations, so you'd need some sort of generalized deletion/insertion correcting code.
I just know that a 6-bit code isn't going to be enough. Sooner or later people will want lower-case, accented character, Japanese, etc. So you might as well come up with a way to put Unicode into DNA, probably as UTF-8. And people will want arbitrary byte data. My approach would be to use four DNA base pairs instead of three, and encode bytes. Simply assign A=00, C=01, G=10, and T=11 (for instance), and encode your bytes.
If I were writing an RFC for data storage in DNA, I'd suggest that most of the time you'd want to store the actual data on the web, and just store a link in the DNA. (Similar to how a QR code or tinyurl can link to a website.) The encoded link could be surrounded by a special DNA sequence that indicates a tiny DNA link code. This sequence could also be used to find the link code by using PCR, so you don't need to do a genome sequence on the entire organism to find the watermark. (The existing watermarks are in fact surrounded by fixed sequences, which may be for that purpose.)
I think there should also be some way to tag and structure data that is stored DNA, to indicate what is identification, description, copyright, HTML, owners, and so forth. XML seems like an obvious choice, but embedding XML in living organisms makes me queasy.
Conclusions
Being able to fabricate a living organism from a DNA computer file is an amazing accomplishment of Craig Venter and the JCVI. Embedding the text of a web page in a living organism seems like science fiction, but it's actually happened. Of course the bacterium doesn't actually serve the web page... yet.Sources
- My Arc code
- Singularity Hub: Secret Messages Coded Into DNA Of Venter Synthetic Bacteria
- The Science article: Creation of a Bacterial Cell Controlled by a Chemically Synthesized Genome.
- DNA image, credit Jerome Walker.
- watermark sequences (Figure S1) and genome map (Figure S2)
- Complete genome of Mycoplasma mycoides JCVI-syn1.0. The watermarks appear as mmycWM1, mmcyWM2b, mmycWM4, and mmycWM3.
which applies catastrophe theory (the hot math trend of the 70s) to marriage. To vastly oversimplify, once your relationship is in an unhappy state, it takes a great deal of effort to flip it back to a happy state. This is pretty much the exact opposite of the linear model that Rey uses.
, the Spanish version of 
. It's definitely improving my vocabulary, as there are many words I've needed to look up. I've listed many of them below, in the hopes this list may be helpful to others as well.
