Examining the silicon dies of the Intel 386 processor

You might think of the Intel 386 processor (1985) as just an early processor in the x86 line, but the 386 was a critical turning point for modern computing in several ways.1 First, the 386 moved the x86 architecture to 32 bits, defining the dominant computing architecture for the rest of the 20th century. The 386 also established the overwhelming importance of x86, not just for Intel, but for the entire computer industry. Finally, the 386 ended IBM's control over the PC market, turning Compaq into the architectural leader.

In this blog post, I look at die photos of the Intel 386 processor and explain what they reveal about the history of the processor, such as the move from the 1.5 µm process to the 1 µm process. You might expect that Intel simply made the same 386 chip at a smaller scale, but there were substantial changes to the chip's layout, even some visible to the naked eye.2 I also look at why the 386 SL had over three times the transistors as the other 386 versions.3

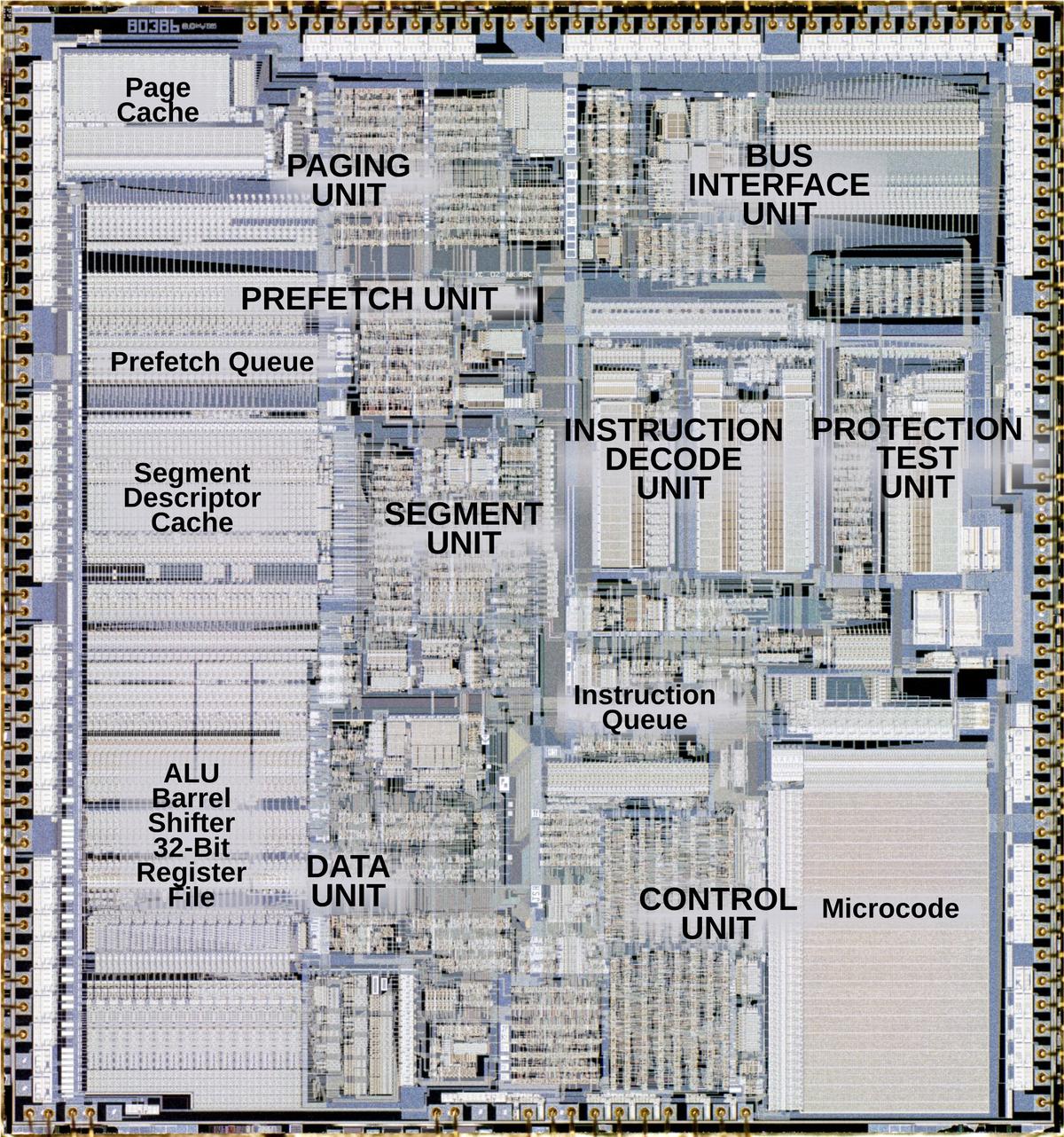
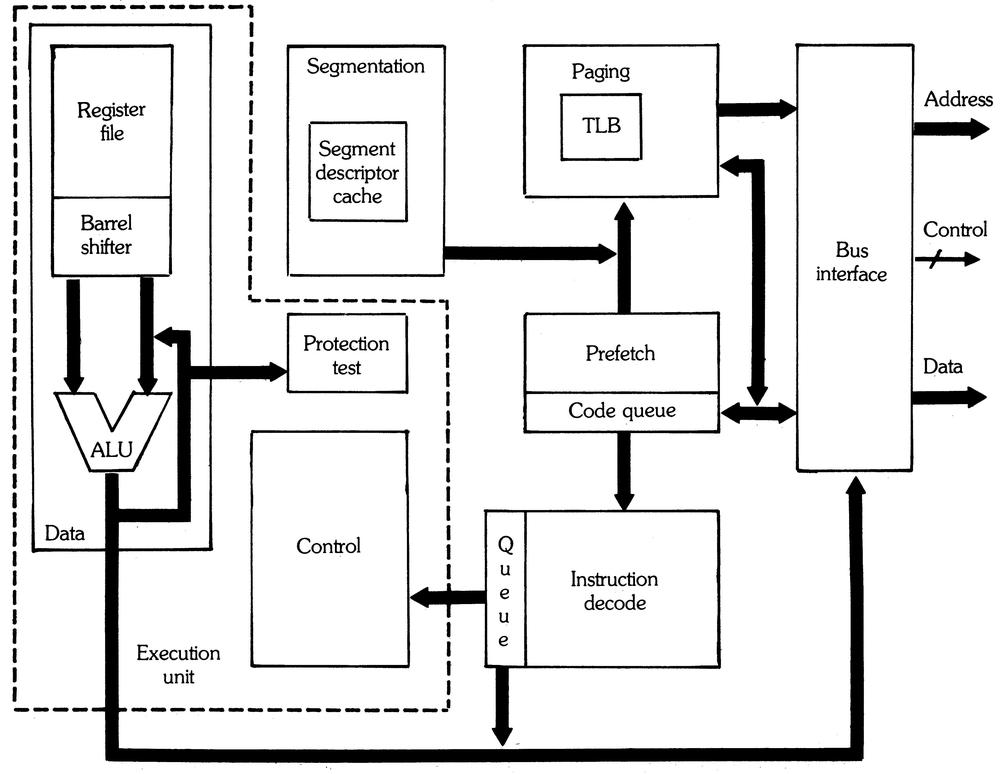
The 80386 was a major advancement over the 286: it implemented a 32-bit architecture, added more instructions, and supported 4-gigabyte segments. The 386 is a complicated processor (by 1980s standards), with 285,000 transistors, ten times the number of the original 8086.4 The 386 has eight logical units that are pipelined5 and operate mostly autonomously.6 The diagram below shows the internal structure of the 386.7

The 386 with the main functional blocks labeled. Click this image (or any other) for a larger version. I created this image using a die photo from Antoine Bercovici.

The heart of a processor is the datapath, the components that hold and process data. In the 386, these components are in the lower left: the ALU (Arithmetic/Logic Unit), a barrel shifter to shift data, and the registers. These components form regular rectangular blocks, 32 bits wide. The datapath, along with the circuitry to the left that manages it, forms the Data Unit. In the lower right is the microcode ROM, which breaks down machine instructions into micro-instructions, the low-level steps of the instruction. The microcode ROM, along with the microcode engine circuitry, forms the Control Unit.

The 386 has a complicated instruction format. The Instruction Decode Unit breaks apart an instruction into its component parts and generates a pointer to the microcode that implements the instruction. The instruction queue holds three decoded instructions. To improve performance, the Prefetch Unit reads instructions from memory before they are needed, and stores them in the 16-byte prefetch queue.8

The 386 implements segmented memory and virtual memory, with access protection.9 The Memory Management Unit consists of the Segment Unit and the Paging Unit: the Segment Unit translates a logical address to a linear address, while the Paging Unit translates the linear address to a physical address. The segment descriptor cache and page cache (TLB) hold data about segments and pages; the 386 has no on-chip instruction or data cache.10 The Bus Interface Unit in the upper right handles communication between the 386 and the external memory and devices.

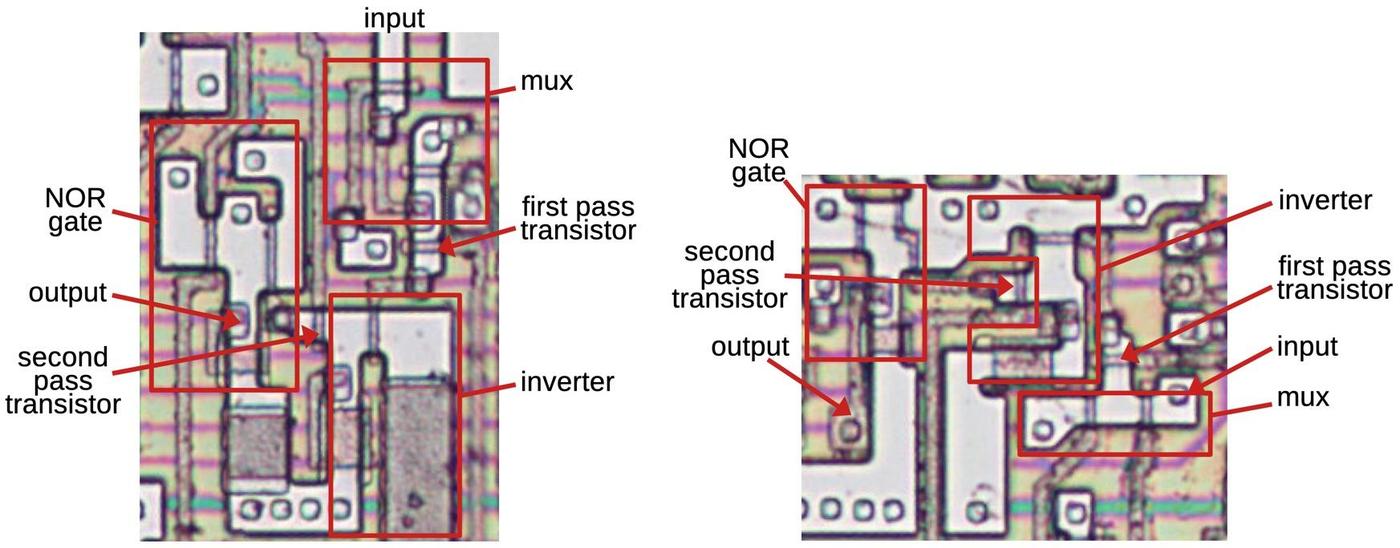
Silicon dies are often labeled with the initials of the designers. The 386 DX, however, has an unusually large number of initials. In the image below, I have enlarged the tiny initials so they are visible. I think the designers put their initials next to the unit they worked on, but I haven't been able to identify most of the names.11

The 386 die with the initials magnified.

The shrink from 1.5 µm to 1 µm

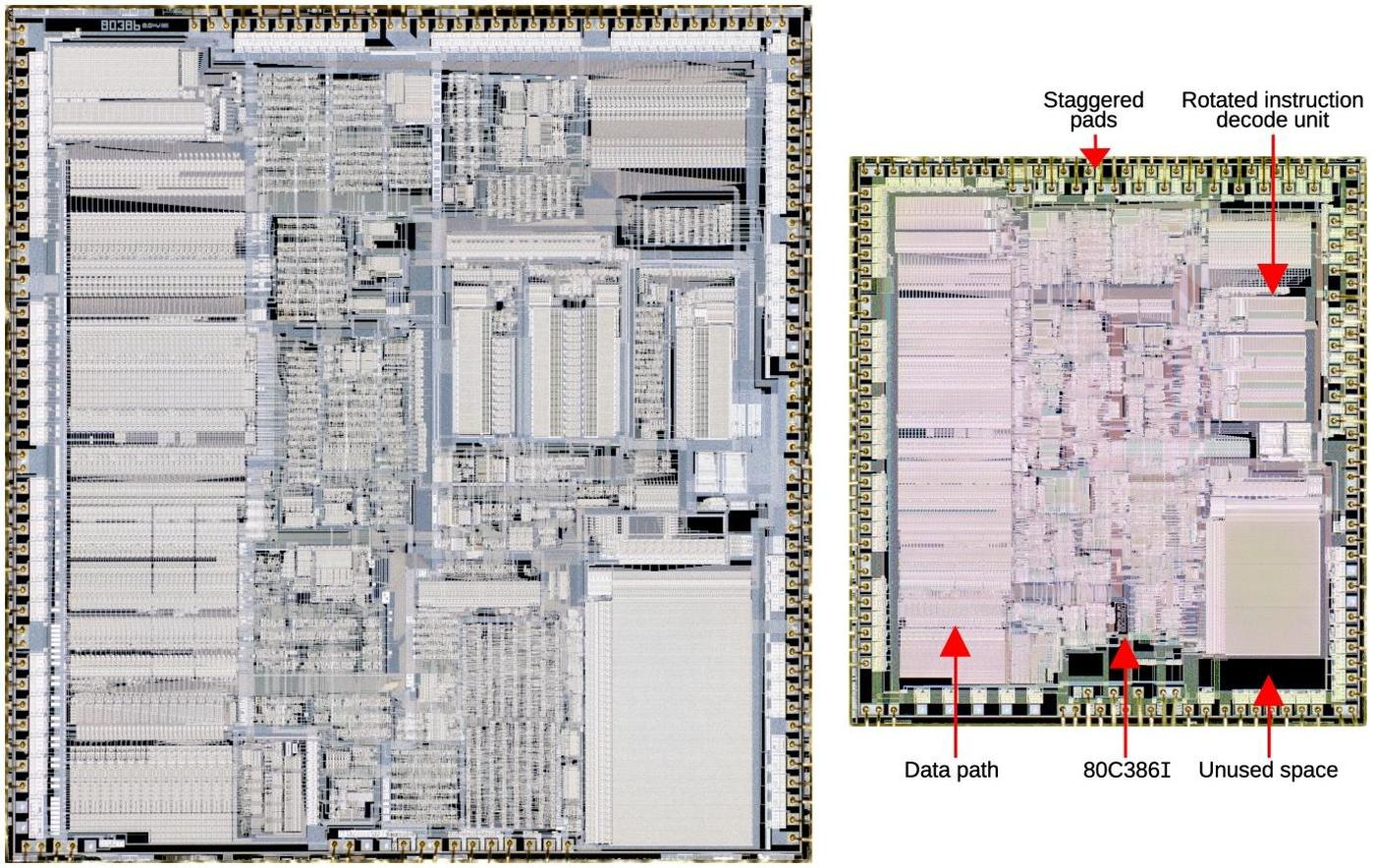
The original 386 was built on a process called CHMOS-III that had 1.5 µm features (specifically the gate channel length for a transistor). Around 1987, Intel moved to an improved process called CHMOS-IV, with 1 µm features, permitting a considerably smaller die for the 386. However, shrinking the layout wasn't a simple mechanical process. Instead, many changes were made to the chip, as shown in the comparison diagram below. Most visibly, the Instruction Decode Unit and the Protection Unit in the center-right are horizontal in the smaller die, rather than vertical. The standard-cell logic (discussed later) is considerably more dense, probably due to improved layout algorithms. The data path (left) was highly optimized in the original so it remained essentially unchanged, but smaller. One complication is that the bond pads around the border needed to remain the same size so bond wires could be attached. To fit the pads around the smaller die, many of the pads are staggered. Because different parts of the die shrank differently, the blocks no longer fit together as compactly, creating wasted space at the bottom of the die. For some reason, the numerous initials on the original 386 die were removed. Finally, the new die was labeled 80C386I with a copyright date of 1985, 1987; it is unclear what "C" and "I" indicate.

Comparison of the 1.5 µm die and the 1 µm die at the same scale. Photos courtesy of Antoine Bercovici.

The change from 1.5 µm to 1 µm may not sound significant, but it reduced the die size by 60%. This allowed more dies on a wafer, substantially dropping the manufacturing cost.12 The strategy of shrinking a processor to a new process before designing a new microarchitecture for the process became Intel's tick-tock strategy.

The 386 SX

In 1988, Intel introduced the 386 SX processor, the low-cost version of the 386, with a 16-bit bus instead of a 32-bit bus. (This is reminiscent of the 8088 processor with an 8-bit bus versus the 8086 processor with a 16-bit bus.) According to the 386 oral history, the cost of the original 386 die decreased to the point where the chip's package cost about as much as the die. By reducing the number of pins, the 386 SX could be put in a one-dollar plastic package and sold for a considerably reduced price. The SX allowed Intel to segment the market, moving low-end customers from the 286 to the 386 SX, while preserving the higher sales price of the original 386, now called the DX.13 In 1988, Intel sold the 386 SX for $219, at least $100 less than the 386 DX. A complete SX computer could be $1000 cheaper than a similar DX model.

For compatibility with older 16-bit peripherals, the original 386 was designed to support a mixture of 16-bit and 32-bit buses, dynamically switching on a cycle-by-cycle basis if needed. Because 16-bit support was built into the 386, the 386 SX didn't require much design work. (Unlike the 8088, which required a redesign of the 8086's bus interface unit.)

The 386 SX was built at both 1.5 µm and 1 µm. The diagram below compares the two sizes of the 386 SX die. These photos may look identical to the 386 DX photos in the previous section, but close examination shows a few differences. Since the 386 SX uses fewer pins, it has fewer bond pads, eliminating the staggered pads of the shrunk 386 DX. There are a few differences at the bottom of the chip, with wiring in much of the 386 DX's wasted space.

Comparison of two dies for the 386 SX. Photos courtesy of Antoine Bercovici.

Comparing the two SX revisions, the larger die is labeled "80P9"; Intel's internal name for the chip was "P9", using their confusing series of P numbers. The shrunk die is labeled "80386SX", which makes more sense. The larger die is copyright 1985, 1987, while the shrunk die (which should be newer) is copyright 1985 for some reason. The larger die has mostly the same initials as the DX, with a few changes. The shrunk die has about 21 sets of initials.

The 386 SL die

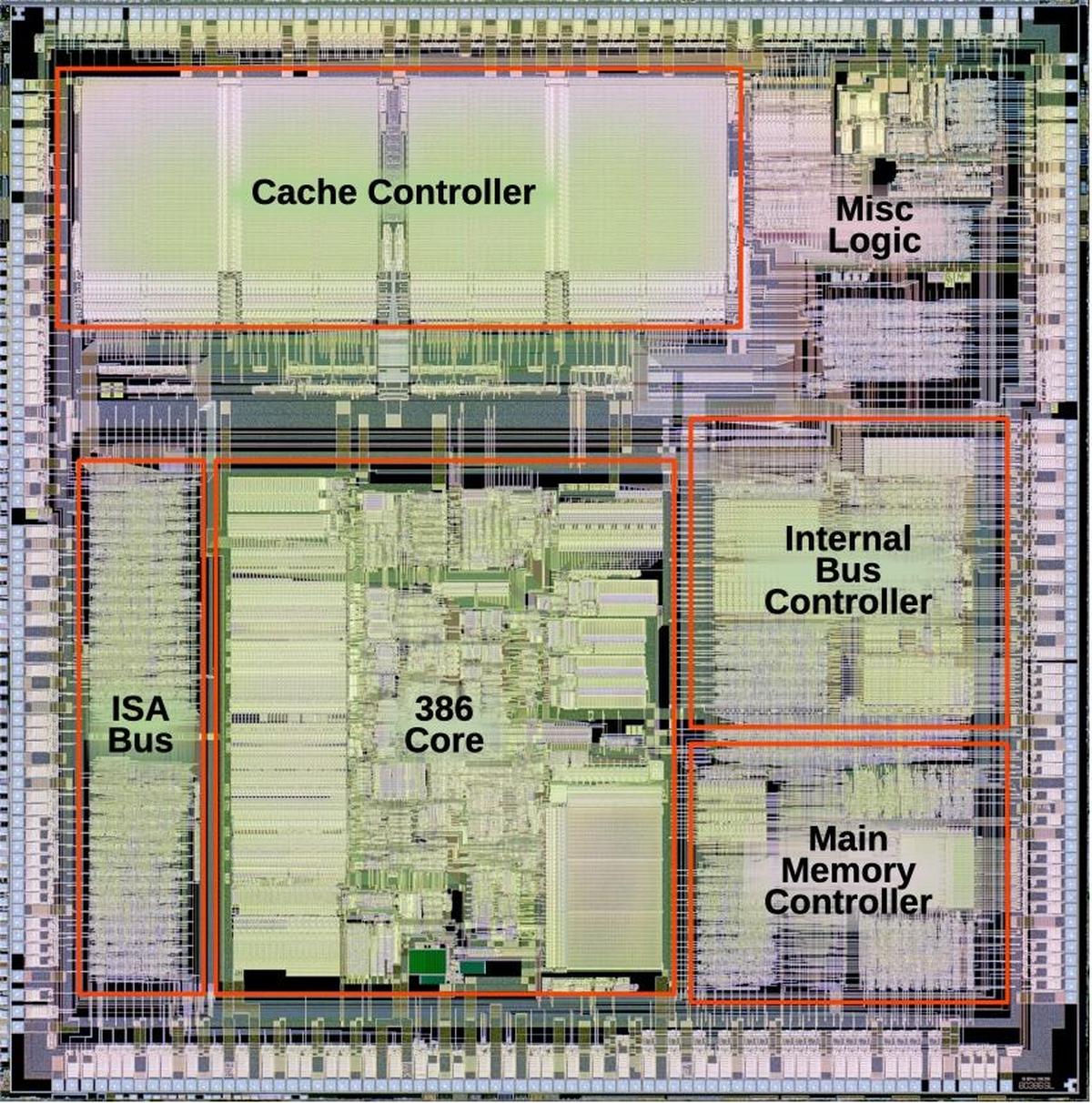
The 386 SL (1990) was a major extension to the 386, combining a 386 core and other functions on one chip to save power and space. Named "SuperSet", it was designed to corner the notebook PC market.14 The 386 SL chip included an ISA bus controller, power management logic, a cache controller for an external cache, and the main memory controller.

Looking at the die photo below, the 386 core itself takes up about 1/4 of the SL's die. The 386 core is very close to the standard 386 DX, but there are a few visible differences. Most visibly, the bond pads and pin drivers have been removed from the core. There are also some circuitry changes. For instance, the 386 SL core supports the System Management Mode, which suspends normal execution, allowing power management and other low-level hardware tasks to be performed outside the regular operating system. System Management Mode is now a standard part of the x86 line, but it was introduced in the 386 SL.

The 386 SL die with functional blocks labeled. Die photo courtesy of Antoine Bercovici.

In total, the 386 SL contains 855,000 transistors,15 over 3 times as many as the regular 386 DX. The cache tag RAM takes up a lot of space and transistors. The cache data itself is external; this on-chip circuitry just manages the cache. The other new components are largely implemented with standard-cell logic (discussed below); this is visible as uniform stripes of circuitry, most clearly in the ISA bus controller.

A brief history of the 386

From the modern perspective, it seems obvious for Intel to extend the x86 line from the 286 to the 386, while keeping backward compatibility. But at the time, this path was anything but clear. This history starts in the late 1970s, when Intel decided to build a "micromainframe" processor, an advanced 32-bit processor for object-oriented programming that had objects, interprocess communication, and memory protection implemented in the CPU. This overly ambitious project fell behind schedule, so Intel created a stopgap processor to sell until the micromainframe processor was ready. This stopgap processor was the 16-bit 8086 processor (1978).

In 1981, IBM decided to use the Intel 8088 (an 8086 variant) in the IBM Personal Computer (PC), but Intel did not realize the importance of this at the time. Instead, Intel was focused on their micromainframe processor, also released in 1981 as the iAPX 432, but this became "one of the great disaster stories of modern computing" as the New York Times called it. Intel then reimplemented the ideas of the ill-fated iAPX 432 on top of a RISC architecture, creating the more successful i960.

Meanwhile, things weren't going well at first for the 286 processor, the follow-on to the 808616. Bill Gates and others called its design "brain-damaged". IBM was unenthusiastic about the 286 for their own reasons.17 As a result, the 386 project was a low priority for Intel and the 386 team felt that it was the "stepchild"; internally, the 386 was pitched as another stopgap, not Intel's "official" 32-bit processor.

Despite the lack of corporate enthusiasm, the 386 team came up with two proposals to extend the 286 to a 32-bit architecture. The first was a minimal approach to extend the existing registers and address space to 32 bits. The more ambitious proposal would add more registers and create a 32-bit instruction set that was significantly different from the 8086's 16-bit instruction set. At the time, the IBM PC was still relatively new, so the importance of the installed base of software wasn't obvious; software compatibility was viewed as a "nice to have" feature rather than essential. After much debate, the decision was made around the end of 1982 to go with the minimal proposal, but supporting both segments and flat addressing, while keeping compatibility with the 286.

By 1984, though, the PC industry was booming and the 286 was proving to be a success. This produced enormous political benefits for the 386 team, who saw the project change from "stepchild" to "king". Intel introduced the 386 in 1985, which was otherwise "a miserable year for Intel and the rest of the semiconductor industry," as Intel's annual report put it. Due to an industry-wide business slowdown, Intel's net income "essentially disappeared." Moreover, facing heavy competition from Japan, Intel dropped out of the DRAM business, a crushing blow for a company that got its start in the memory industry. Fortunately, the 386 would change everything.

Given IBM's success with the IBM PC, Intel was puzzled that IBM wasn't interested in the 386 processor, but IBM had a strategy of their own.18 By this time, the IBM PC was being cloned by many competitors, but IBM had a plan to regain control of the PC architecture and thus the market: in 1987, IBM introduced the PS/2 line. These new computers ran the OS/2 operating system instead of Windows and used the proprietary Micro Channel architecture.19 IBM used multiple engineering and legal strategies to make cloning the PS/2 slow, expensive, and risky, so IBM expected they could take back the market from the clones.

Compaq took the risky approach of ignoring IBM and following their own architectural direction.20 Compaq introduced the high-end Deskpro 386 line in September 1986, becoming the first major company to build 386-based computers. An "executive" system, the Deskpro 386 model 40 had a 40-megabyte hard drive and sold for $6449 (over $15,000 in current dollars). Compaq's gamble paid off and the Deskpro 386 was a rousing success.

The Compaq Deskpro 386 in front of the 386 processor (not to scale). From PC Tech Journal, 1987. Curiously, the die image of the 386 has been mirrored, as can be seen both from the positions of the microcode ROM and instruction decoder at the top as well as from the position of the cut corner of the package.

As for IBM, the PS/2 line was largely unsuccessful and failed to become the standard. Rather than regaining control over the PC, "IBM lost control of the PC standard in 1987 when it introduced its PS/2 line of systems."21 IBM exited the PC market in 2004, selling the business to Lenovo. One slightly hyperbolic book title summed it up: "Compaq Ended IBM's PC Domination and Helped Invent Modern Computing". The 386 was a huge moneymaker for Intel, leading to Intel's first billion-dollar quarter in 1990. It cemented the importance of the x86 architecture, not just for Intel but for the entire computing industry, dominating the market up to the present day.22

How the 386 was designed

The design process of the 386 is interesting because it illustrates Intel's migration to automated design systems and heavier use of simulation.23 At the time, Intel was behind the industry in its use of tools so the leaders of the 386 realized that more automation would be necessary to build a complex chip like the 386 on schedule. By making a large investment in automated tools, the 386 team completed the design ahead of schedule. Along with proprietary CAD tools, the team made heavy use of standard Unix tools such as sed, awk, grep, and make to manage the various design databases.

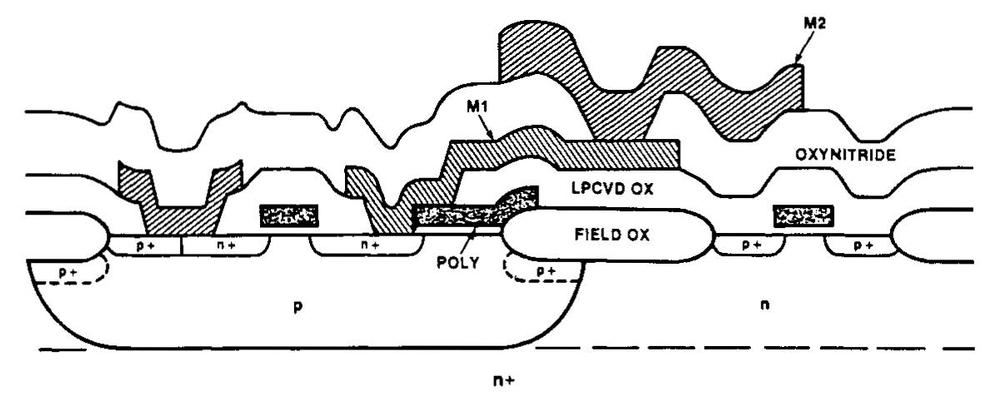
The 386 posed new design challenges compared to the previous 286 processor. The 386 was much more complex, with twice the transistors. But the 386 also used fundamentally different circuitry. While the 286 and earlier processors were built from NMOS transistors, the 386 moved to CMOS (the technology still used today). Intel's CMOS process was called CHMOS-III (complementary high-performance metal-oxide-silicon) and had a feature size of 1.5 µm. CHMOS-III was based on Intel's HMOS-III process (used for the 286), but extended to CMOS. Moreover, the CHMOS process provided two layers of metal instead of one, changing how signals were routed on the chip and requiring new design techniques.

The diagram below shows a cross-section through a CHMOS-III circuit, with an NMOS transistor on the left and a PMOS transistor on the right. Note the jagged three-dimensional topography that is formed as layers cross each other (unlike modern polished wafers). This resulted in the "forbidden gap" problem that caused difficulty for the 386 team. Specifically second-layer metal (M2) could be close to the first-layer metal (M1) or it could be far apart, but an in-between distance would cause problems: the forbidden gap. If the metal layer crossed in the "forbidden gap", the metal could crack and whiskers of metal would touch, causing the chip to fail. These problems reduced the yield of the 386.

A cross-section of circuitry formed with the CHMOS-III process. From A double layer metal CHMOS III technology.

The design of the 386 proceeded both top-down, starting with the architecture definition, and bottom-up, designing standard cells and other basic circuits at the transistor level. The processor's microcode, the software that controlled the chip, was a fundamental component. It was designed with two CAD tools: an assembler and microcode rule checker. The high-level design of the chip (register-level RTL) was created and refined until clock-by-clock and phase-by-phase timing were represented. The RTL was programmed in MAINSAIL, a portable Algol-like language based on SAIL (Stanford Artificial Intelligence Language). Intel used a proprietary simulator called Microsim to simulate the RTL, stating that full-chip RTL simulation was "the single most important simulation model of the 80386".

The next step was to convert this high-level design into a detailed logic design, specifying the gates and other circuitry using Eden, a proprietary schematics-capture system. Simulating the logic design required a dedicated IBM 3083 mainframe that compared it against the RTL simulations. Next, the circuit design phase created the transistor-level design. The chip layout was performed on Applicon and Eden graphics systems. The layout started with critical blocks such as the ALU and barrel shifter. To meet the performance requirements, the TLB (translation lookaside buffer) for the paging mechanism required a creative design, as did the binary adders.

Examples of standard cells used in the 386. From "Automatic Place and Route Used on the 80386" by Joseph Krauskopf and Pat Gelsinger, Intel Technology Journal spring 1986. I have added color.

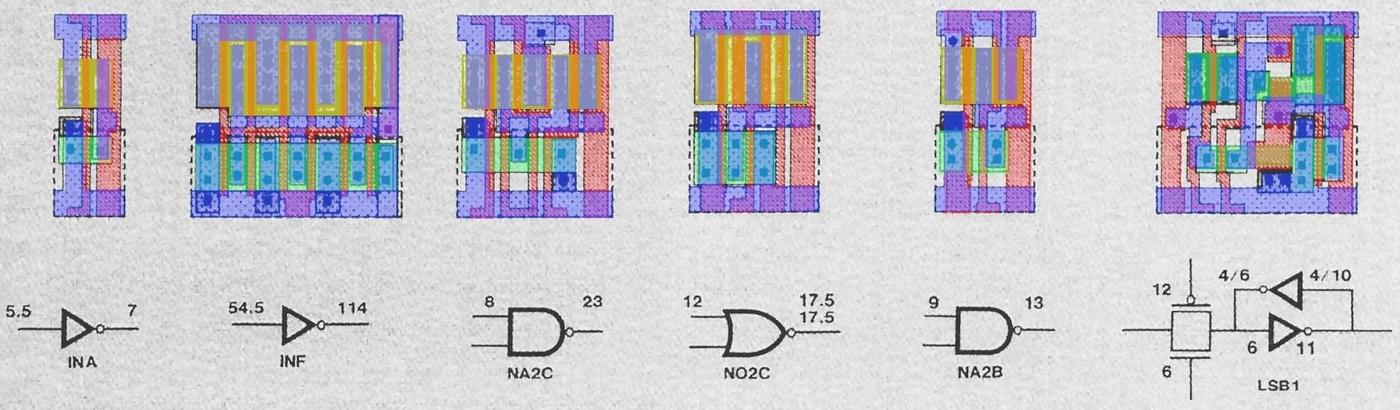
The "random" (unstructured) logic was implemented with standard cells, rather than the transistor-by-transistor design of earlier processors. The idea of standard cells is to have fixed blocks of circuitry (above) for logic gates, flip-flops, and other basic functions.24 These cells are arranged in rows by software to implement the specified logic description. The space between the rows is used as a wiring channel for connections between the cells. The disadvantage of a standard cell layout is that it generally takes up more space than an optimized hand-drawn layout, but it is much faster to create and easier to modify.

These standard cells are visible in the die as regular rows of circuitry. Intel used the TimberWolf automatic placement and routing package, which used simulated annealing to optimize the placement of cells. TimberWolf was built by a Berkeley grad student; one 386 engineer said, "If management had known that we were using a tool by some grad student as the key part of the methodology, they would never have let us use it. " Automated layout was a new thing at Intel; using it improved the schedule, but the lower density raised the risk that the chip would be too large.

Standard cells in the 386. Each row consists of numerous standard cells packed together. Each cell is a simple circuit such as a logic gate or flip flop. The wide wiring channels between the rows hold the wiring that connects the cells. This block of circuitry is in the bottom center of the chip.

The data path consists of the registers, ALU (Arithmetic Logic Unit), barrel shifter, and multiply/divide unit that process the 32-bit data. Because the data path is critical to the performance of the system, it was laid out by hand using a CALMA system. The designers could optimize the layout, taking advantage of regularities in the circuitry, optimizing the shape and size of each transistor and fitting them together like puzzle pieces. The data path is visible on the left side of the die, forming orderly 32-bit-wide rectangles in contrast to the tangles of logic next to it.

Once the transistor-level layout was complete, Intel's Hierarchical Connectivity Verification System checked that the final layout matched the schematics and adhered to the process design rules. The 386 set an Intel speed record, taking just 11 days from completing the layout to "tapeout", when the chip data is sent on magnetic tape to the mask fabrication company. (The tapeout team was led by Pat Gelsinger, who later became CEO of Intel.) After the glass masks were created using an electron-beam process, Intel's "Fab 3" in Livermore (the first to wear the bunnysuits) produced the 386 silicon wafers.

Chip designers like to claim that their chip worked the first time, but that was not the case for the 386. When the team received the first silicon for the 386, they ran a trivial do-nothing test program, "NoOp, NoOp, Halt", and it failed. Fortunately, they found a small fix to a PLA (Programmable Logic Array). Rather than create new masks, they were able to patch the existing mask with ion milling and get new wafers quickly. These wafers worked well enough that they could start the long cycles of debugging and fixing.

Once the processor was released, the problems weren't over.25 Some early 386 processors had a 32-bit multiply problem, where some arguments would unpredictably produce the wrong results under particular temperature/voltage/frequency conditions. (This is unrelated to the famous Pentium FDIV bug that cost Intel $475 million.) The root cause was a layout problem, not a logic problem; they didn't allow enough margin to handle the worst case data in combination with manufacturing process and environment factors. This tricky problem didn't show up in simulation or chip verification, but was only found in stress testing. Intel sold the faulty processors, but marked them as only valid for 16-bit software, while marking the good processors with a double sigma, as seen below.26 This led to embarrassing headlines such as Some 386 Systems Won't Run 32-Bit Software, Intel Says. The multiply bug also caused a shortage of 386 chips in 1987 and 1988 as Intel redesigned the chip to fix the bug. Overall, the 386 issues probably weren't any worse than other processors and the problems were soon forgotten.

Bad and good versions of the 386. Note the labels on the bottom line. Photos (L), (R) by Thomas Nguyen, (CC BY-SA 4.0).

Conclusions

A 17-foot tall plot of the 386. The datapath is on the left and the microcode is in the lower right. It is unclear if this is engineering work or an exhibit at MOMA. Image spliced together from the 1985 annual report.

The 386 processor was a key turning point for Intel. Intel's previous processors sold very well, but this was largely due to heavy marketing ("Operation Crush") and the good fortune to be selected for the IBM PC. Intel was technologically behind the competition, especially Motorola. Motorola had introduced the 68000 processor in 1979, starting a powerful line of (more-or-less) 32-bit processors. Intel, on the other hand, lagged with the "brain-damaged" 16-bit 286 processor in 1982. Intel was also slow with the transition to CMOS; Motorola had moved to CMOS in 1984 with the 68020.

The 386 provided the necessary technological boost for Intel, moving to a 32-bit architecture, transitioning to CMOS, and fixing the 286's memory model and multitasking limitations, while maintaining compatibility with the earlier x86 processors. The overwhelming success of the 386 solidified the dominance of the x86 and Intel, and put other processor manufacturers on the defensive. Compaq used the 386 to take over PC architecture leadership from IBM, leading to the success of Compaq, Dell, and other companies, while IBM eventually departed the PC market entirely. Thus, the 386 had an oversized effect on the computer industry, shaping the winners and losers for decades.

I plan to write more about the 386, so follow me on Twitter @kenshirriff or RSS for updates. I'm also on Mastodon occasionally as @[email protected]. Acknowledgements: The die photos are courtesy of Antoine Bercovici; you should follow him on Twitter as @Siliconinsid.27 Thanks to Pat Gelsinger and Roxanne Koester for providing helpful papers.

Notes and references

1. The 386 also changed the industry because Intel abandoned the standard practice of second sourcing (allowing other companies to manufacture a chip). AMD, for example, had been a second source for the 286. But Intel decided to keep production of the 386 to themselves. Intel ended up licensing the 386 to IBM, though, as the IBM 386SLC. Despite the name, this was the 386 SX, not the 386 SL. ↩

2. Intel made various keychains containing the 386 die, as shown at CPU World. If you know where to look, it is easy to distinguish the variants. In particular, look at the instruction decoders above the microcode and see if they are oriented vertically (pre-shrink 386) or horizontally (post-shrink 386). ↩

3. The naming of the 386 versions is a bit of a mess. The 386 started as the 80386 and later the i386. The 80386SX was introduced in 1988; this is the version with a 16-bit bus. The "regular" 386 was then renamed the DX to distinguish it from the SX. There are several other versions of the 386 that I won't discuss here, such as the EX, CXSB, and 80376. See Wikipedia for details.

   Confusingly, the 486 also used the SX and DX names, but in a different way. The 486 DX was the original that included a floating-point unit, while floating-point was disabled in the 486 SX. Thus, in both cases "DX" was the full chip, while "SX" was the low-cost version, but the removed functionality was entirely different.

   Another complication is that a 386DX chip will have a marking like "SX217", but this has nothing to do with the 386 SX. SX217 is an Intel S-Specification number, which specifies the particular stepping of the processor, indicating a manufacturing change or if a feature has been fixed or removed. ↩

4. Counting transistors isn't as straightforward as you might think. For example, a ROM may have a transistor for a 1 bit and no transistor for a 0 bit. Thus, the number of transistors depends on the data stored in the ROM. Likewise, a PLA has transistors present or absent in a grid, depending on the desired logic functions. For this reason, transistor counts are usually the number of "transistor sites", locations that could have a transistor, even if a transistor is not physically present. In the case of the 386, it has 285,000 transistor sites and 181,000 actual transistors (source), so over 100,000 reported transistors don't actually exist.

   I'll also point out that most sources claim 275,000 transistors for the 386. My assumption is that 285,000 is the more accurate number (since this source distinguishes between transistor sites and physical transistors), while 275,000 is the rounded number. ↩

5. The 386's independent, pipelined functional units provide a significant performance improvement and the pipeline can be executing up to eight instructions at one time. For instance, the 386's microcode engine permits some overlap between the end of one instruction and the beginning of the next, an overlap that speeds up the processor by about 9%. But note that instructions are still executed sequentially, taking multiple clocks per instruction, so it is nothing like the superscalar execution introduced in the Pentium. ↩

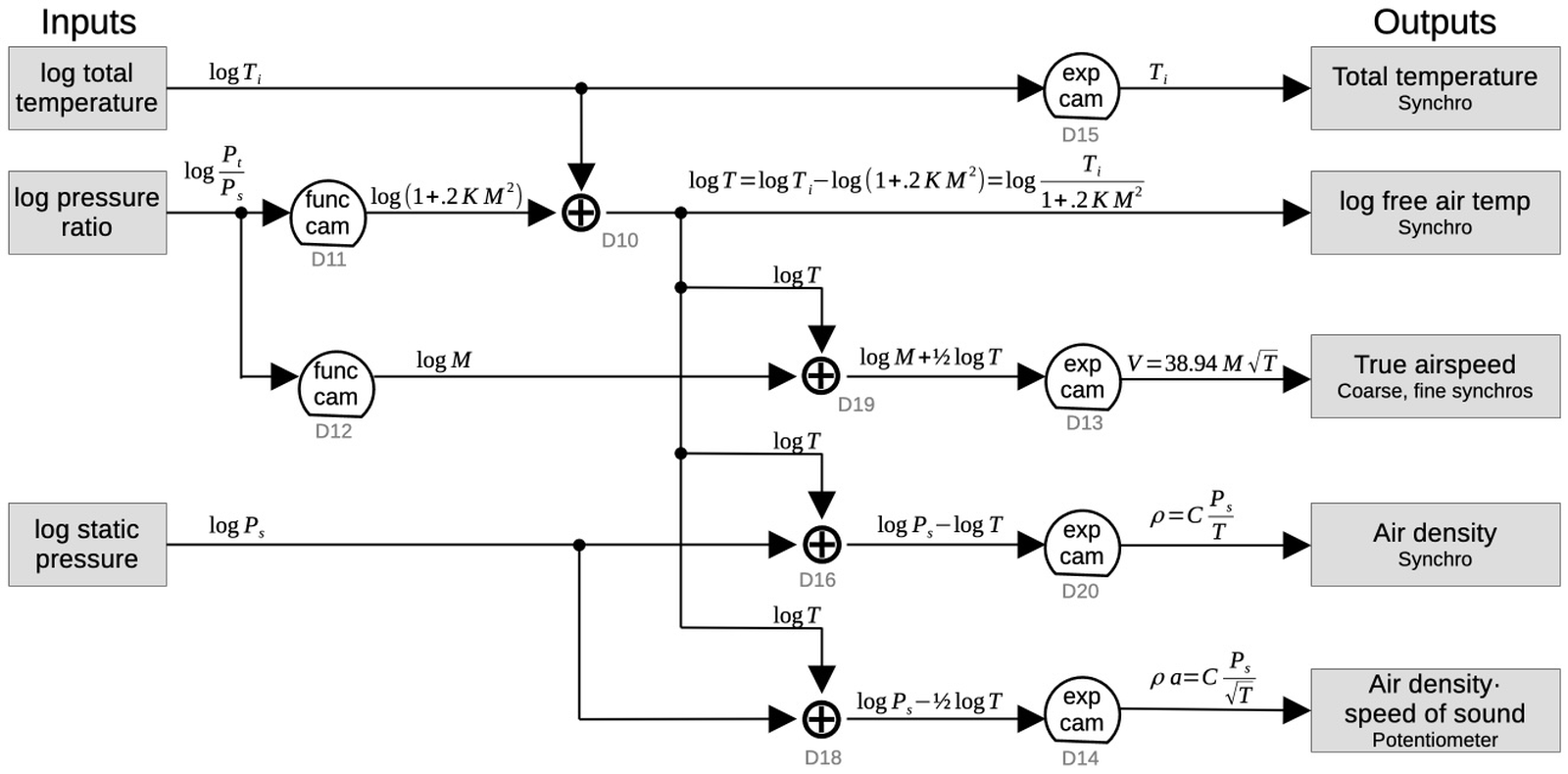
6. The diagram of the 386 die shows eight functional units. It can be compared to the block diagram below, which shows how the units are interconnected.

   

   Block diagram of the 386. From The Intel 80386—Architecture and Implementation.

    ↩

7. My labeled die diagram combines information from two Intel papers: The Intel 80386—Architecture and Implementation and Design and Test of the 80386. The former paper describes the eight functional units. The latter paper provides more details, but only shows six functional units. (The Control Unit and Data Unit are combined into the Execution Unit, while the Protection Test Unit is dropped as an independent unit.) Interestingly, the second paper is by Patrick Gelsinger, who is now CEO of Intel. Pat Gelsinger also wrote "80386 Tapeout - Giving Birth to an Elephant", which says there are nine functional units. I don't know what the ninth unit is, maybe the substrate bias generator? In any case, the count of functional units is flexible.

   

   Patrick Gelsinger's biography from his 80386 paper.

    ↩

8. The 386 has a 16-byte prefetch queue, but apparently only 12 bytes are used due to a pipeline bug (details). ↩

9. Static checks for access violations are performed by the Protection Test Unit, while dynamic checks are performed by the Segment Unit and the Paging Unit. ↩

10. The 386 was originally supposed to have an on-chip cache, but there wasn't room and the cache was dropped in the middle of the project. As it was, the 386 die barely fit into the lithography machine's field of view. ↩

11. It kind of looks like the die has the initials ET next to a telephone. Could this be a reference to the movie E.T. and its catchphrase "E.T. phone home"? "SEC" must be senior mask designer Shirley Carter. "KF" is engineer Kelly Fitzpatrick. "PSR" is probably Paul S. Ries who designed the 386's paging unit. ↩

12. I think that Intel used a 6" (150mm) wafer for the 386. With a 10mm×10mm die, about 128 chips would fit on a wafer. But with a 6mm×6.5mm die, about 344 would fit on a wafer, over 2.5 times as many. (See Die per wafer estimator.) ↩

13. The 286 remained popular compared to the 386, probably due to its lower price. It wasn't until 1991 that the number of 386 units sold exceeded the 286 (source). Intel's revenue for the 386 was much, much higher than for the 286 though (source). ↩

14. The "SuperSet" consisted of the 386 SL along with the 82360SL peripheral I/O chip. The I/O chip contained various ISA bus peripherals, taking the place of multiple chips such as the 8259 that dated back to the 8080 processor. The I/O chip included DMA controllers, timers, interrupt controllers, a real time clock, serial ports, and a parallel port. It also had a hard disk interface, a floppy disk controller, and a keyboard controller. ↩

15. The 386 SL transistor count is from the Intel Microprocessor Quick Reference Guide, which contains information on most of Intel's processors. ↩

16. The 186 processor doesn't fit cleanly into the sequence of x86 processors. Specifically, the 186 is an incompatible side-branch, rather than something in the 286, 386, 486 sequence. The 186 was essentially an 8086 that included additional functionality (clock generator, interrupt controller, timers, etc.) to make it more suitable for an emedded system. The 186 was used in some personal computers, but it was incompatible with the IBM PC so it wasn't very popular. ↩

17. IBM didn't want to use the 286 because they were planning to reverse-engineer the 286 and make their own version, a 16-megahertz CMOS version. This was part of IBM's plan to regain control of the PC architecture with the PS/2. Intel told IBM that "the fastest path to a 16-megahertz CMOS 286 is the 386 because it is CMOS and 16-megahertz", but IBM continued on their own 286 path. Eventually, IBM gave up and used Intel's 286 in the PS/2. ↩

18. IBM might have been reluctant to support the 386 processor because of the risk of cutting into sales of IBM's mid-range 4300 mainframe line. An IBM 4381-2 system ran at about 3.3 MIPS and cost $500,000, about the same MIPS performance as 386/16 system for under $10,000. The systems aren't directly comparable, of course, but many customers could use the 386 for a fraction of the price. IBM's sales of 4300 and other systems declined sharply in 1987, but the decline was blamed on DEC's VAX systems.

    

    An IBM 4381 system. The 4381 processor is the large cabinet to the left of the terminals. The cabinets at the back are probably IBM 3380 disk drives. From an IBM 4381 brochure.

     ↩

19. The most lasting influence of the PS/2 was the round purple and green keyboard and mouse ports that were used by most PCs until USB obsoleted them. The PS2 ports are still available on some motherboards and gaming computers.

    

    The PS/2 keyboard and mouse ports on the back of a Gateway PC.

     ↩

20. When Compaq introduced their 386-based system, "they warned IBM that it has but six months to announce a similar machine or be supplanted as the market's standard setter." (source). Compaq turned out to be correct. ↩

21. The quote is from Computer Structure and Logic. ↩

22. Whenever I mention x86's domination of the computing market, people bring up ARM, but ARM has a lot more market share in people's minds than in actual numbers. One research firm says that ARM has 15% of the laptop market share in 2023, expected to increase to 25% by 2027. (Surprisingly, Apple only has 90% of the ARM laptop market.) In the server market, just an estimated 8% of CPU shipments in 2023 were ARM. See Arm-based PCs to Nearly Double Market Share by 2027 and Digitimes. (Of course, mobile phones are almost entirely ARM.) ↩

23. Most of my section on the 386 design process is based on Design and Test of the 80386. The 386 oral history also provides information on the design process. The article Such a CAD! also describes Intel's CAD systems. Amusingly, I noticed that one of its figures (below) used a photo of the 386SL instead of the 386DX, with the result that the text is completely wrong. For instance, what it calls the microcode ROM is the cache tag RAM.

    

    Erroneous description of the 386 layout. I put an X through it so nobody reuses it.

     ↩

24. Intel has published a guide to their 1.5 micron CHMOS III cell library. I assume this is the same standard-cell library that was used for the logic in the 386. The library provided over 150 logic functions. It also provided cell-based versions of the Intel 80C51 microcontroller and various Intel support chips such as the 82C37A DMA controller, the 82C54 interval timer, and the 82C59 interrupt controller.

    

    Die photo of the 82360SL ISA Peripheral I/O Chip, from the 386 SL Data Book.

    Interestingly, the 386 SL's Peripheral I/O chip (the 82360SL) included the functionality of these support chips. Standard-cell construction is visible as the stripes in the die photo (above). Moreover, the layout of the die shows separated blocks, probably corresponding to each embedded chip. I expect that Intel designed standard-cell versions of the controller chips to embed in the I/O chip and then added the chips to the standard-cell library since they were available. ↩

25. For an example of the problems that could require a new stepping of the 386, see Intel backs off 80386 claims but denies chip recast needed (1986). It discusses multitasking issues with the 386, with Intel calling them "minor imperfections" that could cause "little glitches", while others suggested that the chip would need replacement. The bugs fixed in each stepping of the 386 are documented here. ↩

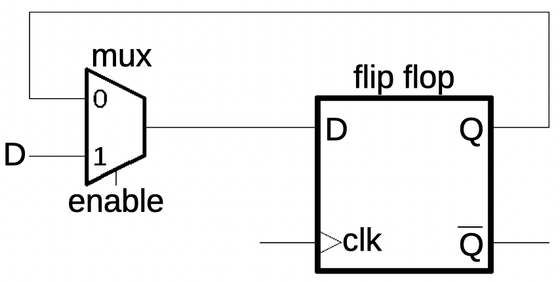
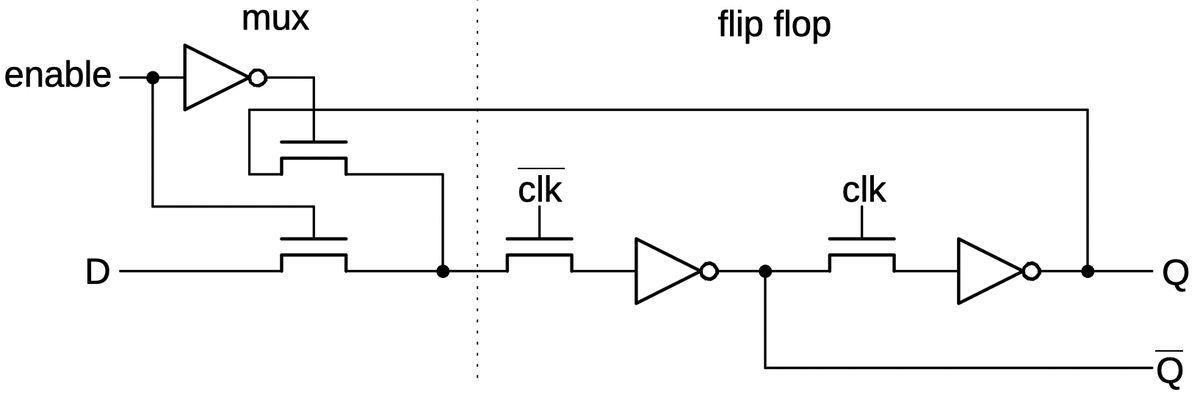
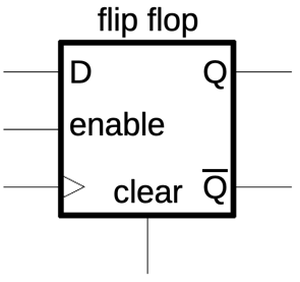
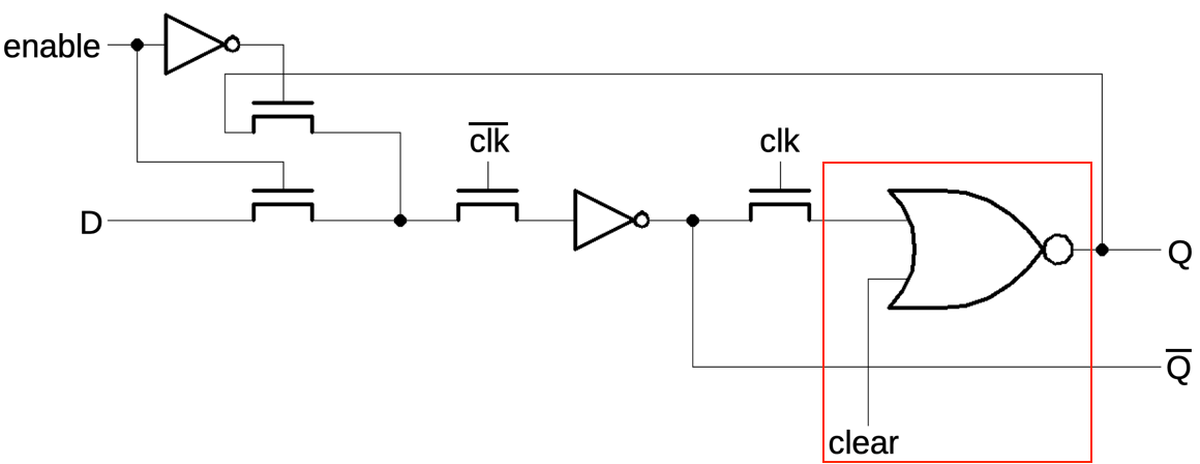
26. One curiosity about the 386 is the IBTS and XBTS instructions. The Insert Bit String and Extract Bit String instructions were implemented in the early 386 processors, but then removed in the B1 stepping. It's interesting that the bit string instructions were removed in the B1 stepping, the same stepping that fixed the 32-bit multiplication bug. Intel said that they were removed "in order to use the area of the chip previously occupied for other microcircuitry" (source). I wonder if Intel fixed the multiplication bug in microcode, and needed to discard the bit string operations to free up enough microcode space. Intel reused these opcodes in the 486 for the CMPXCHG instruction, but that caused conflicts with old 386 programs, so Intel changed the 486 opcodes in the B stepping.  ↩

27. Since Antoine photographed many different 386 chips, I could correlate the S-Specs with the layout changes. I'll summarize the information here, in case anyone happens to want it. The larger DX layout is associated with SX213 and SX215. (Presumably the two are different, but nothing that I could see in the photographs.) The shrunk DX layout is associated with SX217, SX218, SX366, and SX544. The 386 SL image is SX621. ↩

Reverse-engineering the mechanical Bendix Central Air Data Computer

How did fighter planes in the 1950s perform calculations before compact digital computers were available? The Bendix Central Air Data Computer (CADC) is an electromechanical analog computer that used gears and cams for its mathematics. It was used in military planes such as the F-101 and the F-111 fighters, and the B-58 bomber to compute airspeed, Mach number, and other "air data".

The Bendix MG-1A Central Air Data Computer with the case removed, showing the compact gear mechanisms inside. Click this image (or any other) for a larger version.

Aircraft have determined airspeed from air pressure for over a century. A port in the side of the plane provides the static air pressure,1 the air pressure outside the aircraft. A pitot tube points forward and receives the "total" air pressure, a higher pressure due to the speed of the airplane forcing air into the tube. The airspeed can be determined from the ratio of these two pressures, while the altitude can be determined from the static pressure.

But as you approach the speed of sound, the fluid dynamics of air changes and the calculations become very complicated. With the development of supersonic fighter planes in the 1950s, simple mechanical instruments were no longer sufficient. Instead, an analog computer calculated the "air data" (airspeed, air density, Mach number, and so forth) from the pressure measurements. This computer then transmitted the air data electrically to the systems that needed it: instruments, weapons targeting, engine control, and so forth. Since the computer was centralized, the system was called a Central Air Data Computer or CADC, manufactured by Bendix and other companies.

A closeup of the numerous gears inside the CADC. Three differential gear mechanisms are visible.

Each value in the CADC is indicated by the rotational position of a shaft. Compact electric motors rotated the shafts, controlled by magnetic amplifier servos. Gears, cams, and differentials performed computations, with the results indicated by more rotations. Devices called synchros converted the rotations to electrical outputs that controlled other aircraft systems. The CADC is said to contain 46 synchros, 511 gears, 820 ball bearings, and a total of 2,781 major parts (but I haven't counted). These components are crammed into a compact cylinder: 15 inches long and weighing 28.7 pounds.

The equations computed by the CADC are impressively complicated. For instance, one equation is:2

\[~~~\frac{P_t}{P_s} = \frac{166.9215M^7}{( 7M^2-1)^{2.5}}\]

It seems incredible that these functions could be computed mechanically, but three techniques make this possible. The fundamental mechanism is the differential gear, which adds or subtracts values. Second, logarithms are used extensively, so multiplications and divisions become additions and subtractions performed by a differential, while square roots are calculated by gearing down by a factor of 2. Finally, specially-shaped cams implement functions: logarithm, exponential, and functions specific to the application. By combining these mechanisms, complicated functions can be computed mechanically, as I will explain below.

The differential

The differential gear assembly is the mathematical component of the CADC, as it performs addition or subtraction. The differential takes two input rotations and produces an output rotation that is the sum or difference of these rotations.3 Since most values in the CADC are expressed logarithmically, the differential computes multiplication and division when it adds or subtracts its inputs.

A closeup of a differential mechanism.

While the differential functions like the differential in a car, it is constructed differently, with a spur-gear design. This compact arrangement of gears is about 1 cm thick and 3 cm in diameter. The differential is mounted on a shaft along with three co-axial gears: two gears provide the inputs to the differential and the third provides the output. In the photo, the gears above and below the differential are the input gears. The entire differential body rotates with the sum, connected to the output gear at the top through a concentric shaft. (In practice, any of the three gears can be used as the output.) The two thick gears inside the differential body are part of the mechanism.

Note that multiplying a rotation by a constant factor doesn't require a differential; it can be done simply with the ratio between two gears. (If a large gear rotates a small gear, the small gear rotates faster according to the size ratio.) Adding a constant to a rotation is even easier, just a matter of defining what shaft position indicates 0. For this reason, I will ignore constants in the equations.

The cams

The CADC uses cams to implement various functions. Most importantly, cams compute logarithms and exponentials. Cams also implement complicated functions of one variable such as ${M}/{\sqrt{1 + .2 M^2}}$. The function is encoded into the cam's shape during manufacturing, so a hard-to-compute nonlinear function isn't a problem for the CADC. The photo below shows a cam with the follower arm in front. As the cam rotates, the follower moves in and out according to the cam's radius.

A cam inside the CADC implements a function.

However, the shape of the cam doesn't provide the function directly, as you might expect. The main problem with the straightforward approach is the discontinuity when the cam wraps around, which could catch the follower. For example, if the cam implemented an exponential directly, its radius would spiral exponentially and there would be a jump back to the starting value when it wraps around.

Instead, the CADC uses a clever patented method: the cam encodes the difference between the desired function and a straight line. For example, an exponential curve is shown below (blue), with a line (red) between the endpoints. The height of the gray segment, the difference, specifies the radius of the cam (added to the cam's fixed minimum radius). The point is that this difference goes to 0 at the extremes, so the cam will no longer have a discontinuity when it wraps around. Moreover, this technique significantly reduces the size of the value (i.e. the height of the gray region is smaller than the height of the blue line), increasing the cam's accuracy.5

An exponential curve (blue), linear curve (red), and the difference (gray).

To make this work, the cam position must be added to the linear value to yield the result. This is implemented by combining each cam with a differential gear that performs the addition or subtraction.4 As the diagram below shows, the input (23) drives the cam (30) and the differential (25, 37-41). The follower (32) tracks the cam and provides a second input (35) to the differential. The sum from the differential produces the desired function (26).

This diagram, from Patent 2969910, shows how the cam and follower are connected to a differential.

Pressure inputs

The CADC receives two pressure inputs from the pitot tube.6 Inside the CADC, two pressure transducers convert the pressures into rotational positions. Each pressure transducer contains a pair of bellows that expand and contract as the applied pressure changes. The pressure transducer has a tricky job: it must measure tiny pressure changes, but it must also provide a rotational signal that has enough torque to rotate all the gears in the CADC. To accomplish this, each pressure transducer uses a servo loop that drives a motor, controlled by a feedback loop. Cams and differentials convert the rotation into logarithmic values, providing the static pressure as \( log \; P_s \) and the pressure ratio as \( log \; ({P_t}/{P_s}) \) to the rest of the CADC.

The synchro outputs

A synchro is an interesting device that can transmit a rotational position electrically over three wires. In appearance, a synchro is similar to an electric motor, but its internal construction is different, as shown below. Before digital systems, synchros were very popular for transmitting signals electrically through an aircraft. For instance, a synchro could transmit an altitude reading to a cockpit display or a targeting system. Two synchros at different locations have their stator windings connected together, while the rotor windings are driven with AC. Rotating the shaft of one synchro causes the other to rotate to the same position.7

Cross-section diagram of a synchro showing the rotor and stators.

For the CADC, most of the outputs are synchro signals, using compact synchros that are about 3 cm in length. For improved resolution, some of the CADC outputs use two synchros: a coarse synchro and a fine synchro. The two synchros are typically geared in an 11:1 ratio, so the fine synchro rotates 11 times as fast as the coarse synchro. Over the output range, the coarse synchro may turn 180°, providing the approximate output, while the fine synchro spins multiple times to provide more accuracy.

Examining the left section of the CADC

Another view of the CADC.

The Bendix CADC is constructed from modular sections. The right section has the pressure transducers (the black domes), along with the servo mechanisms that control them. The middle section is the "Mach section". In this blog post, I'm focusing on the left section of the CADC, which computes true airspeed, air density, total temperature, log true free air temperature, and air density × speed of sound. I had feared that any attempt at disassembly would result in tiny gears flying in every direction, but the CADC was designed to be taken apart for maintenance. Thus, I could remove the left section of the CADC for analysis.

The diagram below shows the side that connects to the aircraft.8 The various synchros generate the outputs. Some of the synchros have spiral anti-backlash springs installed. These springs prevent wobble in the synchro and gear train as the gears change direction. Three of the exponential cams are visible. The differentials and gears are between the two metal plates, so they are not visible from this angle.

The front of the CADC has multiple output synchros with anti-backlash springs.

Attached to the right side is the temperature transducer, a modular wedge that implements a motorized servo loop to convert the temperature input to a rotation. The servo amplifier consists of three boards of electronic components, including transistors and magnetic amplifiers to drive the motor. The large red potentiometer provides feedback for the servo loop. A flexible cam with 20 adjustment screws allows the transducer to be tuned to eliminate nonlinearities or other sources of error. I'll describe this module in more detail in another post.9

The photo below shows the other side of the section. This communicates with the rest of the CADC through the electrical connector and three gears that mesh with gears in the other section. Two gears receive the pressure signals \( P_t / P_s \) and \(P_s\) from the pressure transducer subsystem. The third gear sends the log total temperature to the rest of the CADC. The electrical connector (a standard 37-pin D-sub) supplies 120 V 400 Hz power to the rest of the CADC and passes synchro signals from the rest of the CADC to the output connectors.

This side of the section interfaces with the rest of the CADC.

The equations

Although the CADC looks like an inscrutable conglomeration of tiny gears, it is possible to trace out the gearing and see exactly how it computes the air data functions. With considerable effort, I have reverse-engineered the mechanisms to create the diagram below, showing how each computation is broken down into mechanical steps. Each line indicates a particular value, specified by a shaft rotation. The ⊕ symbol indicates a differential gear, adding or subtracting its inputs to produce another value. The cam symbol indicates a cam coupled to a differential gear. Each cam computes either a specific function or an exponential, providing the value as a rotation. At the right, the rotations are converted to outputs, either by synchros or a potentiometer. This diagram abstracts out the physical details of the gears. In particular, scaling by constants or reversing the rotation (subtraction versus addition) are not shown.

This diagram shows how the values are computed. The differential numbers are my own arbitrary numbers. Click for a larger version.

I'll go through each calculation briefly.

Total temperature

The external temperature is an important input to the CADC since it affects the air density. A platinum temperature probe provides a resistance that varies with temperature. The resistance is converted to rotation by the temperature transducer, described earlier. The definition of temperature is a bit complicated, though. The temperature outside the aircraft is called the true free air temperature, T. However, the temperature probe measures a higher temperature, called the indicated total air temperature, T_i. The reason for this discrepancy is that when the aircraft is moving at high speed, the air transfers kinetic energy to the temperature probe, heating it up.

The differential and cam D15.

The temperature transducer provides the log of the total temperature as a rotation. At the top of the equation diagram, cam and differential D15 simply take the exponential of this value to determine the total temperature. This rotates the shaft of a synchro to produce the total temperature as an electrical output. As shown above, the D15 cam is attached to the differential by a shaft passing through the metal plate. The follower rotates according to the cam radius, turning the follower gear which meshes with the differential input. The result from the differential is the total temperature.

log free air temperature

A more complicated task of the CADC is to compute the true free air temperature from the measured total temperature. Free air temperature, T, is defined by the formula below, which compensates for the additional heating due to the aircraft's speed. \(T_i\) is the indicated total temperature, M is the Mach number and K is a temperature probe constant.10

\[ T = \frac {T_i} {1 + .2 K M^2 } \]

The diagram below shows the cams, differentials, gear trains, and synchro that compute \(log \; T\). First, cam D11 computes \( log \; (1 + .2 K M^2 ) \). Although that expression is complicated, the key is that it is a function of one variable (M). Thus, it can be computed by cam D11, carefully shaped for this function and attached to differential D11. Differential D10 adds the log total temperature (from the temperature transducer) to produce the desired result. The indicated servo outputs this value to other aircraft systems. (Note that the output is a logarithm; it is not converted to a linear value.11 This value is also fed (via gears) into the calculations of three more equations, below.

The components that compute log free air temperature. D12 is not part of this equation.

Air density

Air density is computed from the static pressure and true temperature:

\[ \rho = C_1 \frac{P_s} {T} \]

It is calculated using logarithms. D16 subtracts the log temperature from the log pressure and cam D20 takes the exponential.

True airspeed

True airspeed is computed from the Mach number and the total temperature according to the following formula:

\[V = 38.94 M \frac{\sqrt{T_i}}{\sqrt{1+.2KM^2}}\]

Substituting the true free air temperature simplifies the formula to the equation implemented in the CADC:

\[V = 38.94 M \sqrt{T} \]

This is computed logarithmically. First, cam and differential D12 compute \(log \; M\) from the pressure ratio.13 Next differential D19 adds half the log temperature to multiply by the square root. Exponential cam D13 removes the logarithms, producing the final result. (The constant 38.94 is an important part of the equation, but is easily implemented with gear ratios.) The output goes to two synchros, geared to provide coarse and fine outputs.12

These components compute true airspeed and air density × speed of sound. Note the large gear driving the coarse synchro and the small gear driving the fine synchro. This causes the fine synchro to rotate at 11 times the speed of the coarse synchro.

Air density × speed of sound

Air density × speed of sound14 is given by the formula

\[ \rho \cdot a = C_2 \frac {P_s} {\sqrt{T}} \]

The calculation is almost the same as the air density calculation. Differential D18 subtracts half the log temperature from the log pressure and then cam D14 computes the exponential. Unlike the other values, this output rotates the shaft of a 1 KΩ potentiometer (above), changing its resistance. I don't know why this particular value is output as a resistance rather than a synchro angle.

Conclusions

The CADC performs nonlinear calculations that seem way too complicated to solve with mechanical gearing. But reverse-engineering the mechanism shows how the equations are broken down into steps that can be performed with cams and differentials, using logarithms for multiplication, division, and square roots. I'll point out that reverse engineering the CADC is not as easy as you might expect. It is difficult to see which gears are in contact, especially when gears are buried in the middle of the CADC and are hard to see. I did much of the reverse engineering by rotating one differential to see which other gears turn, but usually most of the gears turned due to the circuitous interconnections.15

By the late 1960s, as fighter planes became more advanced and computer technology improved, digital processors replaced the gears in air data computers. Garrett AiResearch's ILAAS air data computer (1967) was the first all-digital unit. Other digital systems were Bendix's ADC-1000 Digital Air Data Computer (1967) which was "designed to solve all air data computations at a rate of 75 times per second", Conrac's 3-pound solid-state air data computer (1967), Honeywell's Digital Air Data System (1968), and the LSI-based Garrett AiResearch F-14 CADC (1970). Nonetheless, the gear-based Bendix CADC provides an interesting reverse-engineering challenge as well as a look at the forgotten era of analog computing.

For more background on the CADC, see my overview article on the CADC. I plan to continue reverse-engineering the Bendix CADC and get it operational,16 so follow me on Twitter @kenshirriff or RSS for updates. I've also started experimenting with Mastodon as @oldbytes.space@kenshirriff. Thanks to Joe for providing the CADC. Thanks to Nancy Chen for obtaining a hard-to-find document for me. Marc Verdiell and Eric Schlaepfer are working on the CADC with me.

Notes and references

1. The static air pressure can also be provided by holes in the side of the pitot tube. I couldn't find information indicating exactly how the planes with the CADC received static pressure. ↩

2. Although the CADC's equations may seem ad hoc, they can be derived from fluid dynamics principles. These equations were standardized in the 1950s by various government organizations including the National Bureau of Standards and NACA (the precursor of NASA). ↩

3. Strictly speaking, the output of the differential is the sum of the inputs divided by two. I'm ignoring the factor of 2 because the gear ratios can easily cancel it out. It's also arbitrary whether you think of the differential as adding or subtracting, since it depends on which rotation direction is defined as positive. ↩

4. The cam value will be added or subtracted, depending on whether the function is concave or convex. This is a simple matter of gearing when the values are fed into the differential. Matching the linear segment to the function is also done with gearing that scales the input value appropriately. ↩

5. The diagram below shows a typical cam function in more detail. The input is \(log~ dP/P_s\) and the output is \(log~M / \sqrt{1+.2KM^2}\). The small humped curve at the bottom is the cam correction. Although the input and output functions cover a wide range, the difference that is encoded in the cam is much smaller and drops to zero at both ends.

   

   This diagram, from Patent 2969910, shows how a cam implements a complicated function.

    ↩

6. The CADC also has an input for the "position error correction", which I will ignore in this post. This input provides a correction factor because the measured static pressure may not exactly match the real static pressure. The problem is that the static pressure is measured from a port on the aircraft. Distortions in the airflow may cause errors in this measurement. A separate box, the "compensator", determined the correction factor based on the angle of attack and fed it to the CADC as a synchro signal. ↩

7. Internally, a synchro has a moving rotor winding and three fixed stator windings. When AC is applied to the rotor, voltages are developed on the stator windings depending on the position of the rotor. These voltages produce a torque that rotates the synchros to the same position. In other words, the rotor receives power (26 V, 400 Hz in this case), while the three stator wires transmit the position. The diagram below shows how a synchro is represented schematically, with rotor and stator coils.

   ↩

   The schematic symbol for a synchro.

8. The CADC is wired to the rest of the aircraft through round military connectors. The front panel interfaces these connectors to the D-sub connectors used internally. The two pressure inputs are the black cylinders at the bottom of the photo.

   

   The exterior of the CADC. It is packaged in a rugged metal cylinder.

    ↩

9. I don't have a blog post on the temperature module yet, but I have a description on Twitter and a video. ↩

10. The constant K depends on the recovery factor of the temperature probe. This compensates for a probe where not all of the air's kinetic energy gets transferred to the probe. The 1958 description says that with "modern total temperature probes available today", the K factor can be considered to be 1. ↩

11. The CADC specification says that it provides the log true free air temperature from -80° to +70° C. Obviously the log won't work for a negative value so I assume this is the log of the Kelvin temperature (°K). ↩

12. The CADC specification defines how the parameter values correspond to rotation angles of the synchros. For instance, for the airspeed synchros, the CADC supports the airspeed range 104.3 to 1864.7 knots. The coarse and fine outputs are geared in an 11:1 ratio, so the fine synchro will rotate multiple times over the range to provide more accuracy. Over this range, the coarse synchro rotates from -18.94° to +151.42° and the fine synchro rotates from -208.29° to +1665.68°, with 0° corresponding to 300 knots. ↩

13. The Mach function is defined in terms of \(P_t/P_s \), with separate cases for subsonic and supersonic:

    \[M<1:\] \[~~~\frac{P_t}{P_s} = ( 1+.2M^2)^{3.5}\]

    \[M > 1:\]

    \[~~~\frac{P_t}{P_s} = \frac{166.9215M^7}{( 7M^2-1)^{2.5}}\]

    Although these equations are very complicated, the solution is a function of one variable \(P_t/P_s\) so M can be computed with a single cam. In other words, the mathematics needed to be done when the CADC was manufactured, but once the cam exists, computing M is trivial. ↩

14. I'm not sure why the CADC computes air density times speed of sound. I couldn't find any useful aircraft characteristics that depend on this value, but there must be something. In acoustics and audio, this product is useful as the "air impedance", but I couldn't determine the relevance for aviation. ↩

15. While reverse-engineering this system, I have gained more appreciation for the engineering involved. Converting complicated equations to gearing is a remarkable feat. But also remarkable is designing the CADC as a three-dimensional object that can be built, disassembled, and repaired, long before any sort of 3-D modeling was available. It must have been a puzzle to figure out where to position each differential. Each differential had three gears driving it, which had to mesh with gears from other differentials. There wasn't much flexibility in the gear dimensions, since the gear ratios had to be correct and the number of teeth on each gear had to be an integer. Moreover, it is impressive how tightly the gears are packed together without conflicting with each other. ↩

16. It was very difficult to find information about the CADC. The official military specification is MIL-C-25653C(USAF). After searching everywhere, I was finally able to get a copy from the Technical Reports & Standards unit of the Library of Congress. The other useful document was in an obscure conference proceedings from 1958: "Air Data Computer Mechanization" (Hazen), Symposium on the USAF Flight Control Data Integration Program, Wright Air Dev Center US Air Force, Feb 3-4, 1958, pp 171-194. ↩

How flip-flops are implemented in the Intel 8086 processor

A key concept for a processor is the management of "state", information that persists over time. Much of a computer is built from logic gates, such as NAND or NOR gates, but logic gates have no notion of time. Processors also need a way to hold values, along with a mechanism to move from step to step in a controlled fashion. This is the role of "sequential logic", where the output depends on what happened before. Sequential logic usually operates off a clock signal,1 a sequence of regular pulses that controls the timing of the computer. (If you have a 3.2 GHz processor, for instance, that number is the clock frequency.)

A circuit called the flip-flop is a fundamental building block for sequential logic. A flip-flop can hold one bit of state, a "0" or a "1", changing its value when the clock changes. Flip-flops are a key part of processors, with multiple roles. Several flip-flops can be combined to form a register, holding a value. Flip-flops are also used to build "state machines", circuits that move from step to step in a controlled sequence. A flip-flops can also delay a signal, holding it from from one clock cycle to the next.

Intel introduced the groundbreaking 8086 microprocessor in 1978, starting the x86 architecture that is widely used today. In this blog post, I take a close look at the flip-flops in the 8086: what they do and how they are implemented. In particular, I will focus on the dynamic flip-flop, which holds its value using capacitance, much like DRAM.2 Many of these flip-flops use a somewhat unusual "enable" input, which allows the flip-flop to hold its value for multiple clock cycles.

The 8086 die under the microscope, with the main functional blocks. I count 184 flip-flops with enable and 53 without enable. Click this image (or any other) for a larger version.

The die photo above shows the silicon die of the 8086. In this image, I have removed the metal and polysilicon layers to show the silicon transistors underneath. The colored squares indicate the flip-flops: blue flip-flops have an enable input, while red lack enable. Flip-flops are used throughout the processor for a variety of roles. Around the edges, they hold the state for output pins. The control circuitry makes heavy use of flip-flops for various state machines, such as moving through the "T states" that control the bus cycle. The "loader" uses a state machine to start each instruction. The instruction register, along with some special-purpose registers (N, M, and X) are built with flip-flops. Other flip-flops track the instructions in the prefetch queue. The microcode engine uses flip-flops to hold the current microcode address as well as to latch the 21-bit output from the microcode ROM. The ALU (Arithmetic/Logic Unit) uses flip-flops to hold the status flags, temporary input values, and information on the operation.

The flip-flop circuit

In this section, I'll explain how the flip-flop circuits work, starting with a basic D flip-flop. The D flip-flop (below) takes a data input (D) and stores that value, 0 or 1. The output is labeled Q, while the inverted output is called Q (Q-bar). This flip-flop is "edge triggered", so the storage happens on the edge when the clock changes from low to high.4 Except at this transition, the input can change without affecting the output.

The symbol for a D flip-flop.

The 8086 implements most of its flip-flops dynamically, using pass transistor logic. That is, the capacitance of the wiring (in particular the transistor gate) holds the 0 or 1 state. The dynamic implementation is more compact than the typical static flip-flop implementation, so it is often used in processors. However, the charge on the capacitance will eventually leak away, just like DRAM (dynamic RAM). Thus, the clock must keep going or the values will be lost.3 This behavior is different from a typical flip-flop chip, which will hold its value until the next clock, whether that is a microsecond later or a day later.

The D flip-flop is built from two latch5 stages, each consisting of a pass transistor and an inverter.6 The first pass transistor passes the input value through while the clock is low. When the clock switches high, the first pass transistor turns off and isolates the inverter from the input, but the value persists due to the capacitance (blue arrow). Meanwhile, the second pass transistor switches on, passing the value from the first inverter through the second inverter to the output. Similarly, when the clock switches low, the second transistor switches off but the value is held by capacitance at the green arrow. (The circuit does not need an explicit capacitor; the wiring has enough capacitance to hold the value.) Thus, the output holds the value of the D input that was present at the moment when the clock switched from low to high. Any other changes to the D input do not affect the output.

Schematic of a D flip-flop built from pass transistor logic.

The basic flip-flop can be modified by adding an "enable" input that enables or blocks the clock.7 When the enable input is high, the flip-flop records the D input on the clock edge as before, but when the enable input is low, the flip-flop holds its previous value. The enable input allows the flip-flop to hold its value for an arbitrarily long period of time.

The symbol for the D flip-flop with enable.

The enable flip-flop is constructed from a D flip-flop by feeding the flip-flop's output back to the input as shown below. When the enable input is 0, the multiplexer selects the current Q output as the new flip-flop D input, so the flip-flop retains its previous value. But when the enable input is 1, the multiplexer selects the new D value. (You can think of the enable input as selecting "hold" versus "load".)

Block diagram of a flip-flop with an enable input.

The multiplexer is implemented with two more pass transistors, as shown on the left below.8 When enable is low, the upper pass transistor switches on, passing the current Q output back to the input. When enable is high, the lower pass transistor switches on, passing the D input through to the flip-flop. The schematic below also shows how the inverted Q' output is provided by the first inverter. The circuit "cheats" a bit; since the inverted output bypasses the second transistor, this output can change before the clock edge.

Schematic of a flip-flop with an enable input.

The flip-flops often have a set or clear input, setting the flip-flop high or low. This input is typically connected to the processor's "reset" line, ensuring that the flip-flops are initialized to the proper state when the processor is started. The symbol below shows a flip-flop with a clear input.

The symbol for the D flip-flop with enable and clear inputs.

To support the clear function, a NOR gate replaces the inverter as shown below (red). When the clear input is high, it forces the output from the NOR gate to be low. Note that the clear input is asynchronous, changing the Q output immediately. The inverted Q output, however, doesn't change until clk is high and the output cycles around. A similar modification implements a set input that forces the flip-flop high: a NOR gate replaces the first inverter.

This schematic shows the circuitry for the clear flip-flop.

Implementing a flip-flop in silicon

The diagram below shows two flip-flops as they appear on the die. The bright gray regions are doped silicon, the bottom layer of the chip The brown lines are polysilicon, a layer on top of the silicon. When polysilicon crosses doped silicon, a transistor is formed with a polysilicon gate. The black circles are vias (connections) to the metal layer. The metal layer on top provides wiring between the transistors. I removed the metal layer with acid to make the underlying circuitry visible. Faint purple lines remain on the die, showing where the metal wiring was.

Two flip-flops on the 8086 die.

Although the two flip-flops have the same circuitry, their layouts on the die are completely different. In the 8086, each transistor was carefully shaped and positioned to make the layout compact, so the layout depends on the surrounding logic and the connections. This is in contrast to modern standard-cell layout, which uses a standard layout for each block (logic gate, flip-flop, etc.) and puts the cells in orderly rows. (Intel moved to standard-cell wiring for much of the logic in the the 386 processor since it is much faster to create a standard-cell design than to perform manual layout.)

Conclusions

The flip-flop with enable input is a key part of the 8086, appearing throughout the processor. However, the enable input is a fairly obscure feature for a flip-flop component; most flip-flop chips have a clock input, but not an enable.9 Many FPGA and ASIC synthesis libraries, though, provide it, under the name "D flip-flop with enable" or "D flip-flop with clock enable".

I plan to write more on the 8086, so follow me on Twitter @kenshirriff or RSS for updates. I've also started experimenting with Mastodon recently as @[email protected] so you can follow me there too.

Notes and references

1. Some early computers were asynchronous, such as von Neumann's IAS machine (1952) and its numerous descendants. In this machine, there was no centralized clock. Instead, a circuit such as an adder would send a pulse to the next circuit when it was done, triggering the next circuit in sequence. Thus, instruction execution would ripple through the computer. Although almost all later computers are synchronous, there is active research into asynchronous computing which is potentially faster and lower power. ↩

2. I'm focusing on the dynamic flip-flops in this article, but I'll mention that the 8086 has a few latches built from cross-coupled NOR gates. Most 8086 registers use cross-coupled inverters (static memory cells) rather than flip-flops to hold bits. I explained the 8086 processor's registers in this article. ↩

3. Dynamic circuitry is why the 8086 and many other processors have minimum clock speeds: if the clock is too slow, signals will fade away. For the 8086, the datasheet specifies a maximum clock period of 500 ns, corresponding to a minimum clock speed of 2 megahertz. The CMOS version of the Z80 processor, however, was designed so the clock could be slowed or even stopped. ↩

4. Some flip-flops in the 8086 use the inverted clock, so they transition when the clock switches from high to low. Thus, there are two sets of transitions in the 8068 for each clock cycle. ↩

5. The terminology gets confusing between flip-flops and latches, which sometimes refer to the same thing and sometimes different things. The term "latch" is often used for a flip-flop that operates on the clock level, not the clock edge. That is, when the clock input is high, the input passes through, and when the clock input is low, the value is retained. Confusingly, the clock for a latch is often called "enable". This is different from the enable input that I'm discussing, which is separate from the clock. ↩

6. I asked an Intel chip engineer if they designed the circuitry in the 8086 era in terms of flip-flops. He said that they typically designed the circuitry in terms of the underlying pass transistors and gates, rather than using the flip-flop as a fundamental building block. ↩

7. You might wonder why the clock and enable are separate inputs. Why couldn't you just AND them together so when enable is low, it will block the clock and the flip-flop won't transition? That mostly works, but three factors make it a bad idea. First, the idea of using a clock is so everything changes state at the same time. If you start putting gates in the clock path, the clock gets a bit delayed and shifts the timing. If the delay is too large, the input value might change before the flip-flop can latch it. Thus, putting gates in the clock path is frowned upon. The second factor is that combining the clock and enable signals risks race conditions. For instance, suppose that the enable input goes low and high while the clock remains high. If you AND the two signals together, this will yield a spurious clock edge, causing the flip-flop to latch its input a second time. Finally, if you block the clock for too long, a dynamic flip-flop will lose its value. (Note that the flip-flop circuit used in the 8086 will refresh its value on each clock even if the enable input is held low for a long period of time.) ↩

8. A multiplexer can be implemented with logic gates. However, it is more compact to implement it with pass transistors. The pass transistor implementation takes four transistors (two fewer if the inverted enable signal is already available). A logic gate implementation would take about nine transistors: an AND-OR-INVERT gate, an inverter on the output, and an inverter for the enable signal. ↩

9. The common 7474 is a typical TTL flip-flop that does not have an enable input. Chips with an enable are rarer, such as the 74F377. Strangely, one manufacturer of the 74HC377 shows the enable as affecting the output; I think they simply messed up the schematic in the datasheet since it contradicts the function table.

   Some examples of standard-cell libraries with enable flip-flops: Cypress SoC, Faraday standard cell library, Xilinx Unified Libraries, Infineon PSoC 4 Components, Intel's CHMOS-III cell library (probably used for the 386 processor), and Intel Quartus FPGA. ↩