Reverse-engineering the division microcode in the Intel 8086 processor

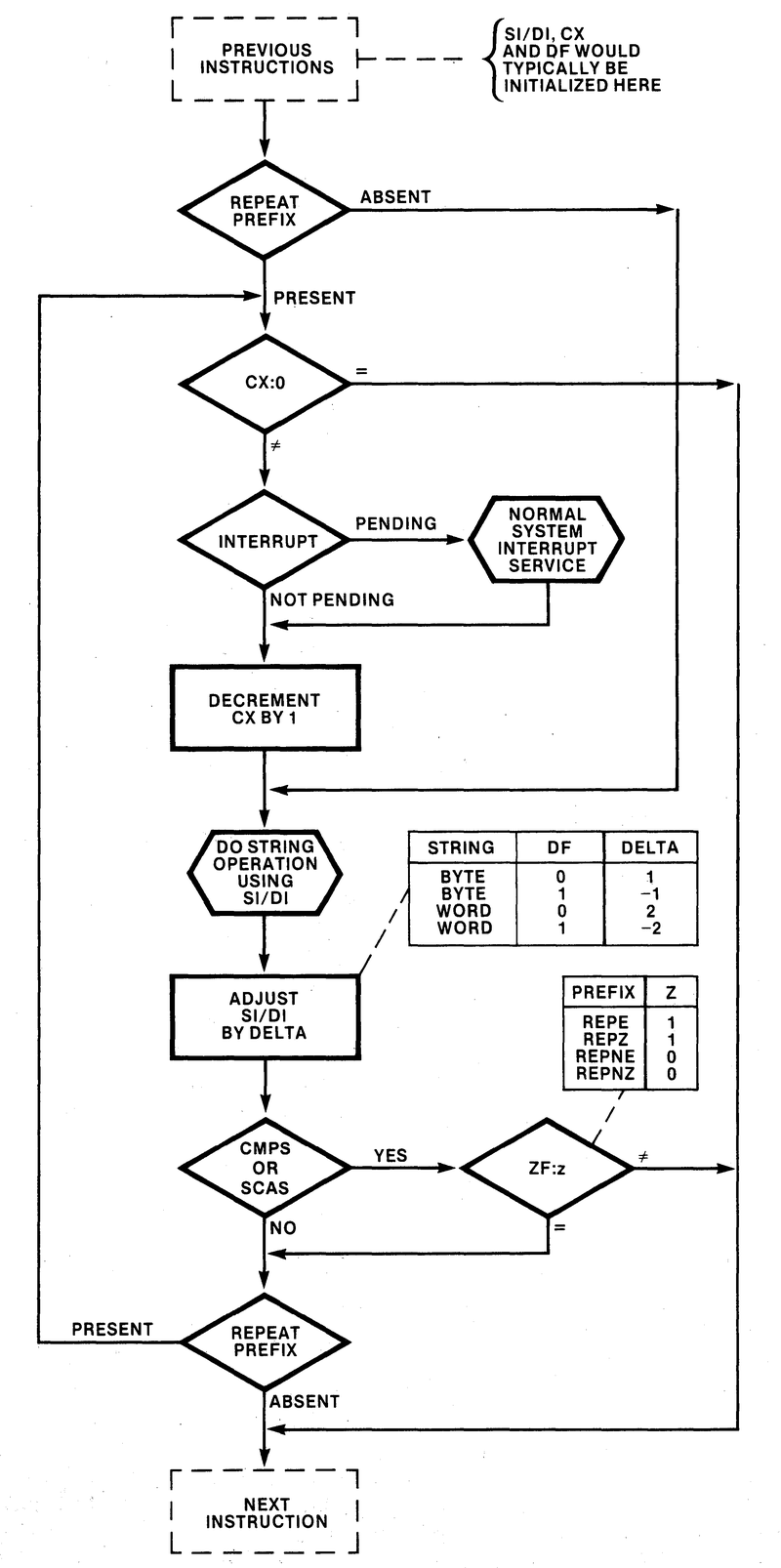
While programmers today take division for granted, most microprocessors in the 1970s could only add and subtract — division required a slow and tedious loop implemented in assembly code. One of the nice features of the Intel 8086 processor (1978) was that it provided machine instructions for integer multiplication and division. Internally, the 8086 still performed a loop, but the loop was implemented in microcode: faster and transparent to the programmer. Even so, division was a slow operation, about 50 times slower than addition.

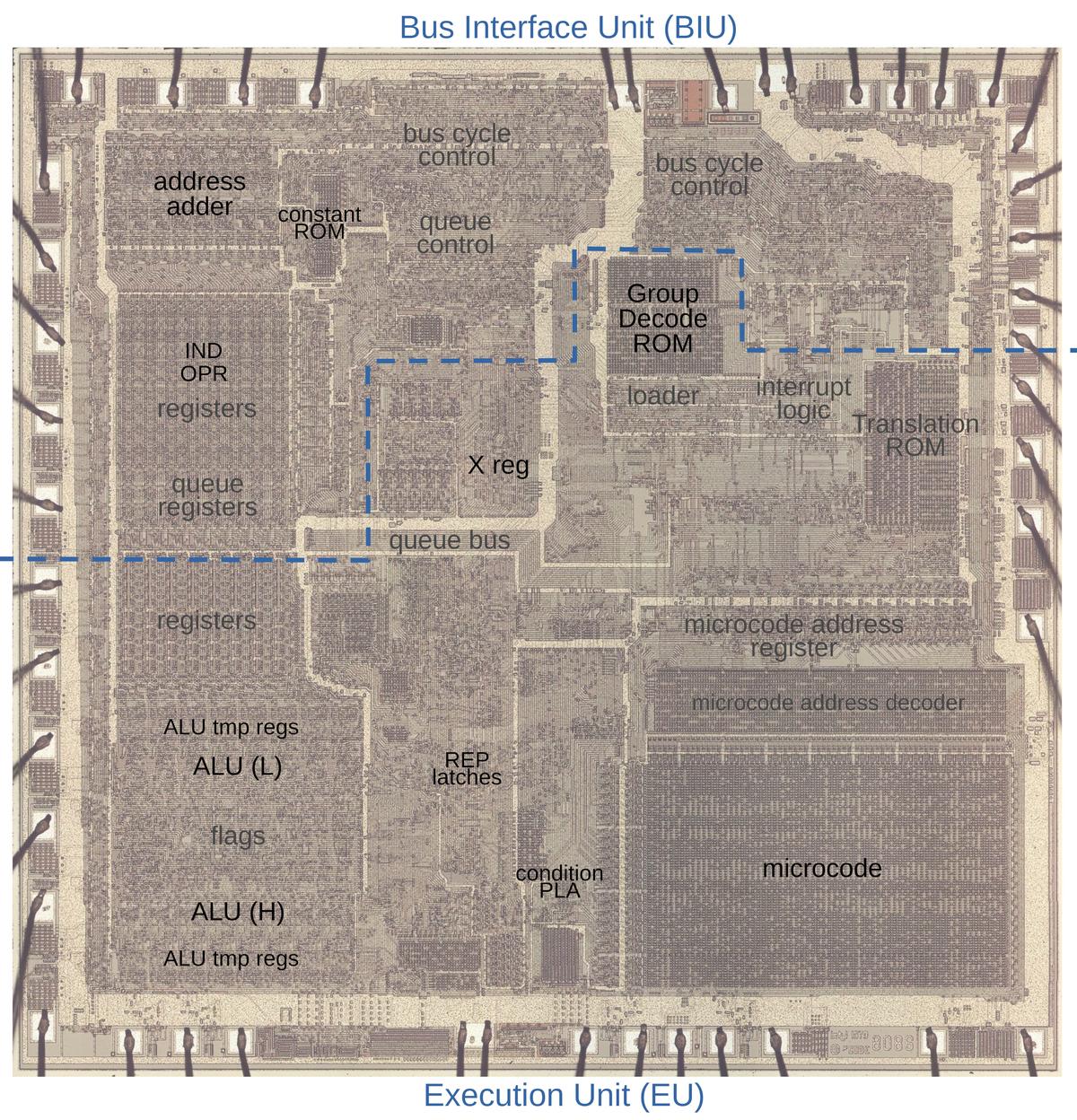
I recently examined multiplication in the 8086, and now it's time to look at the division microcode.1 (There's a lot of overlap with the multiplication post so apologies for any deja vu.) The die photo below shows the chip under a microscope. I've labeled the key functional blocks; the ones that are important to this post are darker. At the left, the ALU (Arithmetic/Logic Unit) performs the arithmetic operations at the heart of division: subtraction and shifts. Division also uses a few special hardware features: the X register, the F1 flag, and a loop counter. The microcode ROM at the lower right controls the process.

The 8086 die under a microscope, with main functional blocks labeled. This photo shows the chip with the metal and polysilicon removed, revealing the silicon underneath. Click on this image (or any other) for a larger version.

Microcode

Like most instructions, the division routines in the 8086 are implemented in microcode. Most people think of machine instructions as the basic steps that a computer performs. However, many processors have another layer of software underneath: microcode. With microcode, instead of building the CPU's control circuitry from complex logic gates, the control logic is largely replaced with code. To execute a machine instruction, the computer internally executes several simpler micro-instructions, specified by the microcode. This is especially useful for a machine instruction such as division, which performs many steps in a loop.

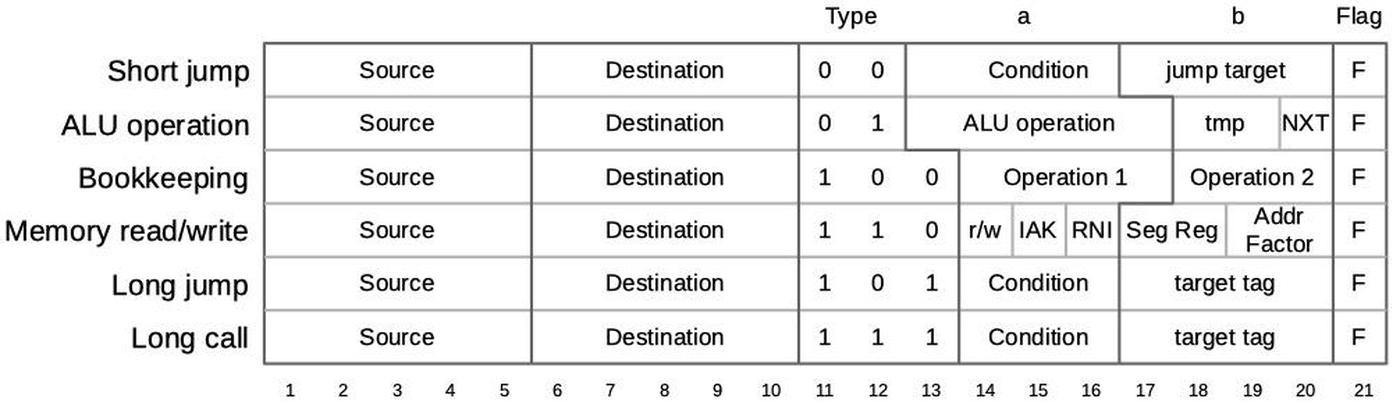
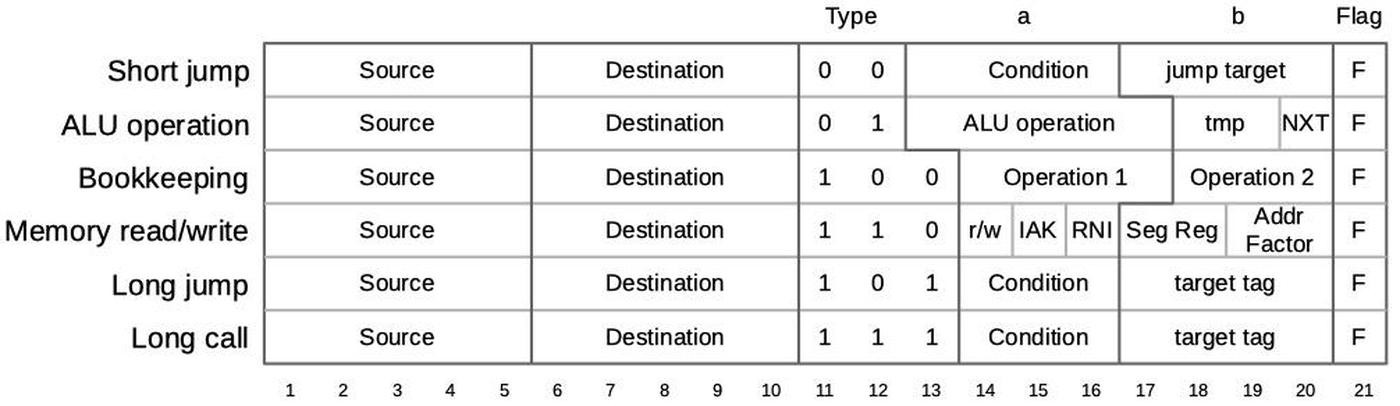
Each micro-instruction in the 8086 is encoded into 21 bits as shown below. Every micro-instruction moves data from a source register to a destination register, each specified with 5 bits. The meaning of the remaining bits depends on the type field and can be anything from an ALU operation to a memory read or write to a change of microcode control flow. Thus, an 8086 micro-instruction typically does two things in parallel: the move and the action. For more about 8086 microcode, see my microcode blog post.

The encoding of a micro-instruction into 21 bits. Based on NEC v. Intel: Will Hardware Be Drawn into the Black Hole of Copyright?

A few details of the ALU (Arithmetic/Logic Unit) operations are necessary to understand the division microcode. The ALU has three temporary registers that are invisible to the programmer: tmpA, tmpB, and tmpC. An ALU operation takes its first argument from the specified temporary register, while the second argument always comes from tmpB. An ALU operation requires two micro-instructions. The first micro-instruction specifies the ALU operation and source register, configuring the ALU. For instance, ADD tmpA to add tmpA to the default tmpB. In the next micro-instruction (or a later one), the ALU result can be accessed through a register called Σ (Sigma) and moved to another register.

The carry flag plays a key role in division. The carry flag is one of the programmer-visible status flags that is set by arithmetic operations, but it is also used by the microcode. For unsigned addition, the carry flag is set if there is a carry out of the word (or byte). For subtraction, the carry flag indicates a borrow, and is set if the subtraction requires a borrow. Since a borrow results if you subtract a larger number from a smaller number, the carry flag also indicates the "less than" condition. The carry flag (and other status flags) are only updated if micro-instruction contains the F bit.

The RCL (Rotate through Carry, Left) micro-instruction is heavily used in the division microcode.2 This operation shifts the bits in a 16-bit word, similar to the << bit-shift operation in high-level languages, but with an additional feature. Instead of discarding the bit on the end, that bit is moved into the carry flag. Meanwhile, the bit formerly in the carry flag moves into the word. You can think of this as rotating the bits while treating the carry flag as a 17th bit of the word. (The RCL operation can also act on a byte.)

The rotate through carry left micro-instruction.

These shifts perform an important part of the division process since shifting can be viewed as multiplying or dividing by two. RCL also provides a convenient way to move the most-significant bit to the carry flag, where it can be tested for a conditional jump. (This is important because the top bit is used as the sign bit.) Another important property is that performing RCL on a lower word and then RCL on an upper word will perform a 32-bit shift, since the high bit of the lower word will be moved into the low bit of the upper word via the carry bit. Finally, the shift moves the quotient bit from the carry into the register.

Binary division

The division process in the 8086 is similar to grade-school long division, except in binary instead of decimal. The diagram below shows the process: dividing 67 (the dividend) by 9 (the divisor) yields the quotient 7 at the top and the remainder 4 at the bottom. Long division is easier in binary than decimal because you don't need to guess the right quotient digit. Instead, at each step you either subtract the divisor (appropriately shifted) or subtract nothing. Note that although the divisor is 4 bits in this example, the subtractions use 5-bit values. The need for an "extra" bit in division will be important in the discussion below; 16-bit division needs a 17-bit value.

								0	1	1	1
1	0	0	1	0	1	0	0	0	0	1	1
				-	0	0	0	0
					1	0	0	0	0
					-	1	0	0	1
						0	1	1	1	1
						-	1	0	0	1
							0	1	1	0	1
							-	1	0	0	1
								0	1	0	0

Instead of shifting the divisor to the right each step, the 8086's algorithm shifts the quotient and the current dividend to the left each step. This trick reduces the register space required. Dividing a 32-bit number (the dividend) by a 16-bit number yields a 16-bit result, so it seems like you'd need four 16-bit registers in total. The trick is that after each step, the 32-bit dividend gets one bit smaller, while the result gets one bit larger. Thus, the dividend and the result can be packed together into 32 bits. At the end, what's left of the dividend is the 16-bit remainder. The table below illustrates this process for a sample dividend (blue) and quotient (green).3 At the end, the 16-bit blue value is the remainder.

dividend																quotient
0	0	0	0	1	1	1	1	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1	0	0	0	0	0	0	0	0
0	0	0	0	1	1	1	0	0	0	0	0	0	1	0	1	1	1	1	1	1	1	1	0	0	0	0	0	0	0	0	0
0	0	0	0	1	1	0	0	0	0	0	0	1	1	1	1	1	1	1	1	1	1	0	0	0	0	0	0	0	0	0	0
0	0	0	0	1	0	0	0	0	0	1	0	0	0	1	1	1	1	1	1	1	0	0	0	0	0	0	0	0	0	0	0
0	0	0	0	0	0	0	0	0	1	0	0	1	0	1	1	1	1	1	1	0	0	0	0	0	0	0	0	0	0	0	0
0	0	0	0	0	0	0	0	1	0	0	1	0	1	1	1	1	1	1	0	0	0	0	0	0	0	0	0	0	0	0	1
0	0	0	0	0	0	0	1	0	0	1	0	1	1	1	1	1	1	0	0	0	0	0	0	0	0	0	0	0	0	1	1
0	0	0	0	0	0	1	0	0	1	0	1	1	1	1	1	1	0	0	0	0	0	0	0	0	0	0	0	0	1	1	1
0	0	0	0	0	1	0	0	1	0	1	1	1	1	1	1	0	0	0	0	0	0	0	0	0	0	0	0	1	1	1	1
0	0	0	0	1	0	0	1	0	1	1	1	1	1	1	0	0	0	0	0	0	0	0	0	0	0	0	1	1	1	1	1
0	0	0	0	0	0	1	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	1	1	1	1	0
0	0	0	0	0	1	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	1	1	1	1	0	1
0	0	0	0	1	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	1	1	1	1	0	1	1
0	0	0	0	1	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0	1	1	1	1	1	0	1	1	0
0	0	0	0	0	0	0	0	0	0	0	0	1	1	0	0	0	0	0	0	0	0	1	1	1	1	1	0	1	1	0	0
0	0	0	0	0	0	0	0	0	0	0	1	1	0	0	0	0	0	0	0	0	1	1	1	1	1	0	1	1	0	0	1
0	0	0	0	0	0	0	0	0	0	1	1	0	0	0	0	0	0	0	0	1	1	1	1	1	0	1	1	0	0	1	1

The division microcode

The 8086 has four division instructions to handle signed and unsigned division of byte and word operands. I'll start by describing the microcode for the unsigned word division instruction DIV, which divides a 32-bit dividend by a 16-bit divisor. The dividend is supplied in the AX and DX registers while the divisor is specified by the source operand. The 16-bit quotient is returned in AX and the 16-bit remainder in DX. For a divide-by-zero, or if the quotient is larger than 16 bits, a type 0 "divide error" interrupt is generated.

CORD: The core division routine

The CORD microcode subroutine below implements the long-division algorithm for all division instructions; I think CORD stands for Core Divide. At entry, the arguments are in the ALU temporary registers: tmpA/tmpC hold the 32-bit dividend, while tmpB holds the 16-bit divisor. (I'll explain the configuration for byte division later.) Each cycle of the loop shifts the values and then potentially subtracts the divisor. One bit is appended to the quotient to indicate whether the divisor was subtracted or not. At the end of the loop, whatever is left of the dividend is the remainder.

Each micro-instruction specifies a register move on the left, and an action on the right. The moves transfer words between the visible registers and the ALU's temporary registers, while the actions are mostly ALU operations or control flow. As is usually the case with microcode, the details are tricky. The first three lines below check if the division will overflow or divide by zero. The code compares tmpA and tmpB by subtracting tmpB, discarding the result, but setting the status flags (F). If the upper word of the divisor is greater or equal to the dividend, the division will overflow, so execution jumps to INT0 to generate a divide-by-zero interrupt.4 (This handles both the case where the dividend is "too large" and the divide-by-0 case.) The number of loops in the division algorithm is controlled by a special-purpose loop counter. The MAXC micro-instruction initializes the counter to 7 or 15, for a byte or word divide instruction respectively.

   move        action
             SUBT tmpA   CORD: set up compare
Σ → no dest  MAXC F       compare, set up counter, update flags
             JMP NCY INT0 generate interrupt if overflow
             RCL tmpC    3: main loop: left shift tmpA/tmpC
Σ → tmpC     RCL tmpA     
Σ → tmpA     SUBT tmpA    set up compare/subtract
             JMPS CY 13   jump if top bit of tmpA was set
Σ → no dest  F            compare, update flags
             JMPS NCY 14  jump for subtract
             JMPS NCZ 3   test counter, loop back to 3
             RCL tmpC    10: done:
Σ → tmpC                  shift last bit into tmpC
Σ → no dest  RTN          done: get top bit, return

             RCY         13: reset carry
Σ → tmpA     JMPS NCZ 3  14: subtract, loop
             JMPS 10     done, goto 10

The main loop starts at 3. The tmpC and tmpA registers are shifted left. This has two important side effects. First, the old carry bit (which holds the latest quotient bit) is shifted into the bottom of tmpC. Second, the top bit of tmpA is shifted into the carry bit; this provides the necessary "extra" bit for the subtraction below. Specifically, if the carry (the "extra" tmpA bit) is set, tmpB can be subtracted, which is accomplished by jumping to 13. Otherwise, the code compares tmpA and tmpB by subtracting tmpB, discarding the result, and updating the flags (F). If there was no borrow/carry (tmpA ≥ tmpB), execution jumps to 14 to subtract. Otherwise, the internal loop counter is decremented and control flow goes back to the top of the loop if not done (NCZ, Not Counter Zero). If the loop is done, tmpC is rotated left to pick up the last quotient bit from the carry flag. Then a second rotate of tmpC is performed but the result is discarded; this puts the top bit of tmpC into the carry flag for use later in POSTIDIV. Finally, the subroutine returns.

The subtraction path is 13 and 14, which subtract tmpB from tmpA by storing the result (Σ) in tmpA. This path resets the carry flag for use as the quotient bit. As in the other path, the loop counter is decremented and tested (NCZ) and execution either continues back at 3 or finishes at 10.

One complication is that the carry bit is the opposite of the desired quotient bit. Specifically, if tmpA < tmpB, the comparison generates a borrow so the carry flag is set to 1. In this case, the desired quotient bit is 0 and no subtraction takes place. But if tmpA ≥ tmpB, the comparison does not generate a borrow (so the carry flag is set to 0), the code subtracts tmpB, and the desired quotient bit is 1. Thus, tmpC ends up holding the complement of the desired result; this is fixed later.

The microcode is carefully designed to pack the divide loop into a small number of micro-instructions. It uses the registers and the carry flag in tricky ways, using the carry flag to hold the top bit of tmpA, the comparison result, and the generated quotient bit. This makes the code impressively dense but tricky to understand.

The top-level division microcode

Now I'll pop up a level and take a look at the top-level microcode (below) that implements the DIV and IDIV machine instructions. The first three instructions load tmpA, tmpC, and tmpB from the specified registers. (The M register refers to the source specified in the instruction, either a register or a memory location.) Next, the X0 condition tests bit 3 of the instruction, which in this case distinguishes DIV from IDIV. For signed division (IDIV), the microcode calls PREIDIV, which I'll discuss below. Next, the CORD micro-subroutine discussed above is called to perform the division.

DX → tmpA                      iDIV rmw: load tmpA, tmpC, tmpB 
AX → tmpC    RCL tmpA           set up RCL left shift operation
M → tmpB     CALL X0 PREIDIV    set up integer division if IDIV
             CALL CORD          call CORD to perform division 
             COM1 tmpC          set up to complement the quotient 
DX → tmpB    CALL X0 POSTIDIV   get original dividend, handle IDIV
Σ → AX       NXT                store updated quotient
tmpA → DX    RNI                store remainder, run next instruction

As discussed above, the quotient in tmpC needs to be 1's-complemented, which is done with COM1. For IDIV, the micro-subroutine POSTIDIV sets the signs of the results appropriately. The results are stored in the AX and DX registers. The NXT micro-operation indicates the next micro-instruction is the last one, directing the microcode engine to start the next machine instruction. Finally, RNI directs the microcode engine to run the next machine instruction.

8-bit division

The 8086 has separate opcodes for 8-bit division. The 8086 supports many instructions with byte and word versions, using 8-bit or 16-bit arguments respectively. In most cases, the byte and word instructions use the same microcode, with the ALU and register hardware using bytes or words based on the instruction. In the case of division, the shift micro-operations act on tmpA and tmpC as 8-bit registers rather than 16-bit registers. Moreover, the MAXC micro-operation initializes the internal counter to 7 rather than 15. Thus, the same CORD microcode is used for word and byte division, but the number of loops and the specific operations are changed by the hardware.

The diagram below shows the tmpA and tmpC registers during each step of dividing 0x2345 by 0x34. Note that the registers are treated as 8-bit registers. The divisor (blue) steadily shrinks with the quotient (green) taking its place. At the end, the remainder is 0x41 (blue) and the quotient is 0xad, complement of the green value.

tmpA																tmpC
0	0	0	0	0	0	0	0	0	0	1	0	0	0	1	1	0	0	0	0	0	0	0	0	0	1	0	0	0	1	0	1
0	0	0	0	0	0	0	0	0	0	0	1	0	0	1	0	0	0	0	0	0	0	0	0	1	0	0	0	1	0	1	0
0	0	0	0	0	0	0	0	0	0	1	0	0	1	0	1	0	0	0	0	0	0	0	0	0	0	0	1	0	1	0	1
0	0	0	0	0	0	0	0	0	0	0	1	0	1	1	0	0	0	0	0	0	0	0	0	0	0	1	0	1	0	1	0
0	0	0	0	0	0	0	0	0	0	1	0	1	1	0	0	0	0	0	0	0	0	0	0	0	1	0	1	0	1	0	1
0	0	0	0	0	0	0	0	0	0	1	0	0	1	0	0	0	0	0	0	0	0	0	0	1	0	1	0	1	0	1	0
0	0	0	0	0	0	0	0	0	0	0	1	0	1	0	1	0	0	0	0	0	0	0	0	0	1	0	1	0	1	0	0
0	0	0	0	0	0	0	0	0	0	1	0	1	0	1	0	0	0	0	0	0	0	0	0	1	0	1	0	1	0	0	1
0	0	0	0	0	0	0	0	0	0	1	0	0	0	0	1	0	0	0	0	0	0	0	0	0	1	0	1	0	0	1	0

Although the CORD routine is shared for byte and word division, the top-level microcode is different. In particular, the byte and word division instructions use different registers, requiring microcode changes. The microcode below is the top-level code for byte division. It is almost the same as the microcode above, except it uses the top and bottom bytes of the accumulator (AH and AL) rather than the AX and DX registers.

AH → tmpA                     iDIV rmb: get arguments
AL → tmpC    RCL tmpA          set up RCL left shift operation
M → tmpB     CALL X0 PREIDIV   handle signed division if IDIV
             CALL CORD         call CORD to perform division
             COM1 tmpC         complement the quotient
AH → tmpB    CALL X0 POSTIDIV  handle signed division if IDIV
Σ → AL       NXT               store quotient
tmpA → AH    RNI               store remainder, run next instruction

Signed division

The 8086 (like most computers) represents signed numbers using a format called two's complement. While a regular byte holds a number from 0 to 255, a signed byte holds a number from -128 to 127. A negative number is formed by flipping all the bits (known as the one's complement) and then adding 1, yielding the two's complement value. For instance, +5 is 0x05 while -5 is 0xfb. (Note that the top bit of a number is set for a negative number; this is the sign bit.) The nice thing about two's complement numbers is that the same addition and subtraction operations work on both signed and unsigned values. Unfortunately, this is not the case for signed multiplication and division.

The 8086 has separate IDIV (Integer Divide) instructions to perform signed division. The 8086 performs signed division by converting the arguments to positive values, performing unsigned division, and then negating the results if necessary. As shown earlier, signed and unsigned division both use the same top-level microcode and the microcode conditionally calls some subroutines for signed division. These additional subroutines cause a significant performance penalty, making signed division over 20 cycles slower than unsigned division. I will discuss those micro-subroutines below.

PREIDIV

The first subroutine for signed division is PREIDIV, performing preliminary operations for integer division. It converts the two arguments, stored in tmpA/tmpC and tmpB, to positive values. It keeps track of the signs using an internal flag called F1, toggling this flag for each negative argument. This conveniently handles the rule that two negatives make a positive since complementing the F1 flag twice will clear it. The point of this is that the main division code (CORD) only needs to handle unsigned division.

The microcode below implements PREIDIV. First it tests if tmpA is negative, but the 8086 does not have a microcode condition to directly test the sign of a value. Instead, the microcode determines if a value is negative by shifting the value left, which moves the top (sign) bit into the carry flag. The conditional jump (NCY) then tests if the carry is clear, jumping if the value is non-negative. If tmpA is negative, execution falls through to negate the first argument. This is tricky because the argument is split between the tmpA and tmpC registers. The two's complement operation (NEG) is applied to the low word, while either 2's complement or one's complement (COM1) is applied to the upper word, depending on the carry for mathematical reasons.5 The F1 flag is complemented to keep track of the sign. (The multiplication process reuses most of this code, starting at the NEGATE entry point.)

Σ → no dest             PREIDIV: shift tmpA left
             JMPS NCY 7  jump if non-negative
             NEG tmpC   NEGATE: negate tmpC
Σ → tmpC     COM1 tmpA F maybe complement tmpA
             JMPS CY 6  
             NEG tmpA    negate tmpA if there's no carry
Σ → tmpA     CF1        6: toggle F1 (sign)

             RCL tmpB  7: test sign of tmpB
Σ → no dest  NEG tmpB    maybe negate tmpB
             JMPS NCY 11 skip if tmpB positive
Σ → tmpB     CF1 RTN     else negate tmpB, toggle F1 (sign)
             RTN        11: return

The next part of the code, starting at 7, negates tmpB (the divisor) if it is negative. Since the divisor is a single word, this code is simpler. As before, the F1 flag is toggled if tmpB is negative. At the end, both arguments (tmpA/tmpC and tmpB) are positive, and F1 indicates the sign of the result.

POSTIDIV

After computing the result, the POSTIDIV routine is called for signed division. The routine first checks for a signed overflow and raises a divide-by-zero interrupt if so. Next, the routine negates the quotient and remainder if necessary.6

In more detail, the CORD routine left the top bit of tmpC (the complemented quotient) in the carry flag. Now, that bit is tested. If the carry bit is 0 (NCY), then the top bit of the quotient is 1 so the quotient is too big to fit in a signed value.7 In this case, the INT0 routine is executed to trigger a type 0 interrupt, indicating a divide overflow. (This is a rather roundabout way of testing the quotient, relying on a carry bit that was set in a previous subroutine.)

             JMP NCY INT0 POSTIDIV: if overflow, trigger interrupt
             RCL tmpB      set up rotate of tmpB
Σ → no dest  NEG tmpA      get sign of tmpB, set up negate of tmpA
             JMPS NCY 5    skip if tmpB non-negative
Σ → tmpA                   otherwise negate tmpA (remainder)
             INC tmpC     5: set up increment
             JMPS F1 8     test sign flag, skip if set
             COM1 tmpC     otherwise set up complement
             CCOF RTN     8: clear carry and overflow flags, return

Next, tmpB (the divisor) is rotated to see if it is negative. (The caller loaded tmpB with the original divisor, replacing the dividend that was in tmpB previously.) If the divisor is negative, tmpA (the remainder) is negated. This implements the 8086 rule that the sign of the remainder matches the sign of the divisor.

The quotient handling is a bit tricky. Recall that tmpC holds the complemented quotient. the F1 flag is set if the result should be negative. In that case, the complemented quotient needs to be incremented by 1 (INC) to convert from 1's complement to 2's complement. On the other hand, if the quotient should be positive, 1's-complementing tmpC (COM1) will yield the desired positive quotient. In either case, the ALU is configured in POSTIDIV, but the result will be stored back in the main routine.

Finally, the CCOF micro-operation clears the carry and overflow flags. Curiously, the 8086 documentation declares that the status flags are undefined following IDIV, but the microcode explicitly clears the carry and overflow flags. I assume that the flags were cleared in analogy with MUL, but then Intel decided that this wasn't useful so they didn't document it. (Documenting this feature would obligate them to provide the same functionality in later x86 chips.)

The hardware for division

For the most part, the 8086 uses the regular ALU addition and shifts for the division algorithm. Some special hardware features provide assistance. In this section, I'll look at this hardware.

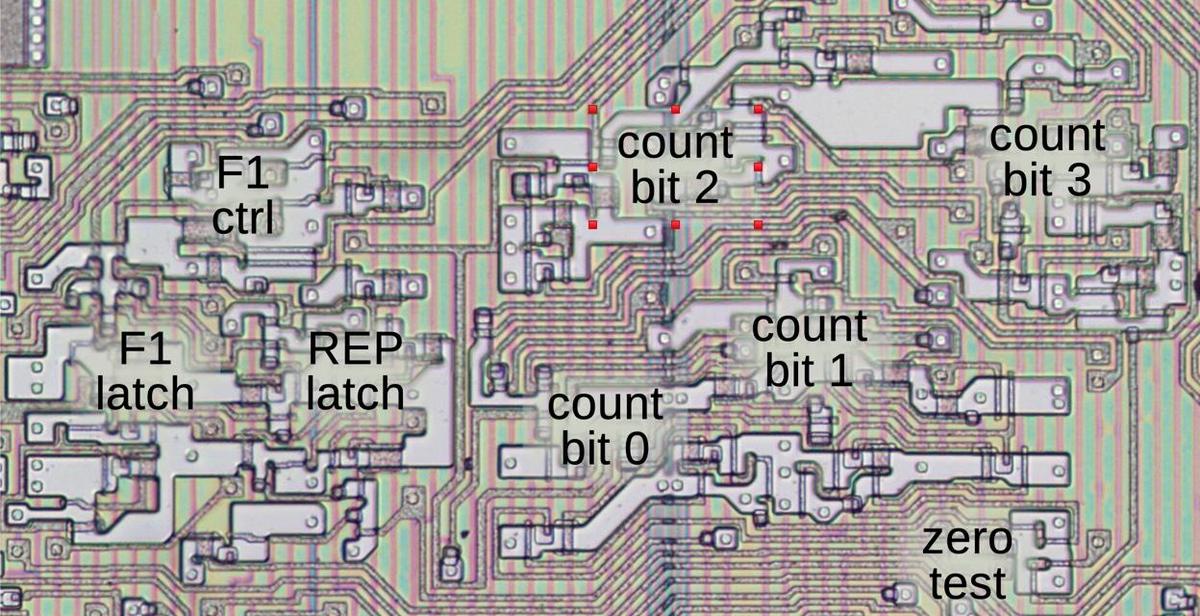
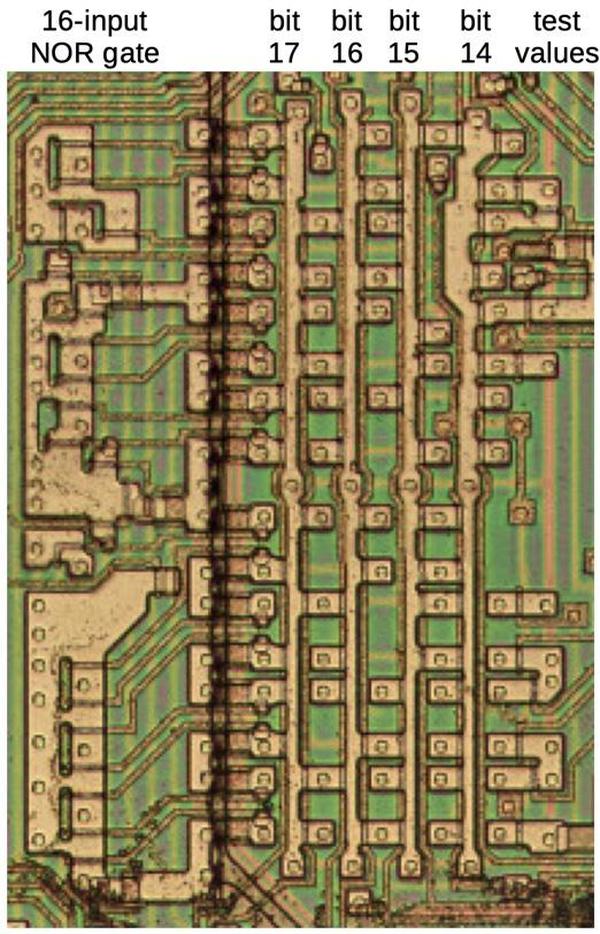
Loop counter

The 8086 has a 4-bit loop counter for multiplication and division. This counter starts at 7 for byte division and 15 for word division, based on the low bit of the opcode. This loop counter allows the microcode to decrement the counter, test for the end, and perform a conditional branch in one micro-operation. The counter is implemented with four flip-flops, along with logic to compute the value after decrementing by one. The MAXC (Maximum Count) micro-instruction sets the counter to 7 or 15 for byte or word operations respectively. The NCZ (Not Counter Zero) micro-instruction has two actions. First, it performs a conditional jump if the counter is nonzero. Second, it decrements the counter.

The F1 flag

Signed multiplication and division use an internal flag called F18 to keep track of the sign. The F1 flag is toggled by microcode through the CF1 (Complement F1) micro-instruction. The F1 flag is implemented with a flip-flop, along with a multiplexer to select the value. It is cleared when a new instruction starts, set by a REP prefix, and toggled by the CF1 micro-instruction. The diagram below shows how the F1 latch and the loop counter appear on the die. In this image, the metal layer has been removed, showing the silicon and the polysilicon wiring underneath.

The counter and F1 latch as they appear on the die. The latch for the REP state is also here.

X register

The division microcode uses an internal register called the X register to distinguish between the DIV and IDIV instructions. The X register is a 3-bit register that holds the ALU opcode, indicated by bits 5–3 of the instruction.9 Since the instruction is held in the Instruction Register, you might wonder why a separate register is required. The motivation is that some opcodes specify the type of ALU operation in the second byte of the instruction, the ModR/M byte, bits 5–3.10 Since the ALU operation is sometimes specified in the first byte and sometimes in the second byte, the X register was added to handle both these cases.

For the most part, the X register indicates which of the eight standard ALU operations is selected (ADD, OR, ADC, SBB, AND, SUB, XOR, CMP). However, a few instructions use bit 0 of the X register to distinguish between other pairs of instructions. For instance, it distinguishes between MUL and IMUL, DIV and IDIV, CMPS and SCAS, MOVS and LODS, or AAA and AAS. While these instruction pairs may appear to have arbitrary opcodes, they have been carefully assigned so the microcode can distinguish them.

The implementation of the X register is straightforward, consisting of three flip-flops to hold the three bits of the instruction. The flip-flops are loaded from the prefetch queue bus during First Clock and during Second Clock for appropriate instructions, as the instruction bytes travel over the bus. Testing bit 0 of the X register with the X0 condition is supported by the microcode condition evaluation circuitry, so it can be used for conditional jumps in the microcode.

Algorithmic and historical context

As you can see from the microcode, division is a complicated and relatively slow process. On the 8086, division takes up to 184 clock cycles to perform all the microcode steps. (In comparison, two registers can be added in 3 clock cycles.) Multiplication and division both loop over the bits, performing repeated addition or subtraction respectively. But division requires a decision (subtract or not?) at each step, making it even slower, about half the speed of multiplication.11

Various algorithms have been developed to speed up division. Rather than performing long division one bit at a time, you can do long division in, say, base 4, producing two quotient bits in each step. As with decimal long division, the tricky part is figuring out what digit to select. The SRT algorithm (1957) uses a small lookup table to estimate the quotient digit from a few bits of the divisor and dividend. The clever part is that the selected digit doesn't need to be exactly right at each step; the algorithm will self-correct after a wrong "guess". The Pentium processor (1993) famously had a floating point division bug due to a few missing values in the SRT table. This bug cost Intel $475 million to replace the faulty processors.

Intel's x86 processors steadily improved divide performance. The 80286 (1982) performed a word divide in 22 clocks, about 6 times as fast as the 8086. In the Penryn architecture (2007), Intel upgraded from Radix-4 to Radix-16 division. Rather than having separate integer and floating-point hardware, integer divides were handled through the floating point divider. Although modern Intel processors have greatly improved multiplication and division compared to the 8086, division is still a relatively slow operation. While a Tiger Lake (2020) processor can perform an integer multiplication every clock cycle (with a latency of 3 cycles), division is much slower and can only be done once every 6-10 clock cycles (details).

I've written numerous posts on the 8086 so far and plan to continue reverse-engineering the 8086 die so follow me on Twitter @kenshirriff or RSS for updates. I've also started experimenting with Mastodon recently as @[email protected].

Notes and references

1. My microcode analysis is based on Andrew Jenner's 8086 microcode disassembly. ↩

2. The 8086 patent and Andrew Jenner's microcode use the name LRCY (Left Rotate through Carry) instead of RCL. I figure that RCL will be more familiar to people because of the corresponding machine instruction. ↩

3. In the dividend/quotient table, the tmpA register is on the left and the tmpC register is on the right. 0x0f00ff00 divided by 0x0ffc yielding the remainder 0x0030 (blue) and quotient 0xf04c (green). (The green bits are the complement of the quotient due to implementation in the 8086.) ↩

4. I described the 8086's interrupt circuitry in detail in this post. ↩

5. The negation code is a bit tricky because the result is split across two words. In most cases, the upper word is bitwise complemented. However, if the lower word is zero, then the upper word is negated (two's complement). I'll demonstrate with 16-bit values to keep the examples small. The number 257 (0x0101) is negated to form -257 (0xfeff). Note that the upper byte is the one's complement (0x01 vs 0xfe) while the lower byte is two's complement (0x01 vs 0xff). On the other hand, the number 256 (0x0100) is negated to form -256 (0xff00). In this case, the upper byte is the two's complement (0x01 vs 0xff) and the lower byte is also the two's complement (0x00 vs 0x00).

   (Mathematical explanation: the two's complement is formed by taking the one's complement and adding 1. In most cases, there won't be a carry from the low byte to the upper byte, so the upper byte will remain the one's complement. However, if the low byte is 0, the complement is 0xff and adding 1 will form a carry. Adding this carry to the upper byte yields the two's complement of that byte.)

   To support multi-word negation, the 8086's NEG instruction clears the carry flag if the operand is 0, and otherwise sets the carry flag. (This is the opposite of the above because subtractions (including NEG) treat the carry flag as a borrow flag, with the opposite meaning.) The microcode NEG operation has identical behavior to the machine instruction, since it is used to implement the machine instruction.

   Thus to perform a two-word negation, the microcode negates the low word (tmpC) and updates the flags (F). If the carry is set, the one's complement is applied to the upper word (tmpA). But if the carry is cleared, the two's complement is applied to tmpA. ↩

6. There is a bit of ambiguity with the quotient and remainder of negative numbers. For instance, consider -27 ÷ 7. -27 = 7 × -3 - 6 = 7 * -4 + 1. So you could consider the result to be a quotient of -3 and remainder of -6, or a quotient of -4 and a remainder of 1. The 8086 uses the rule that the remainder will have the same sign as the dividend, so the first result would be used. The advantage of this rule is that you can perform unsigned division and adjust the signs afterward:
   27 ÷ 7 = quotient 3, remainder 6.
   -27 ÷ 7 = quotient -3, remainder -6.
   27 ÷ -7 = quotient -3, remainder 6.
   -27 ÷ -7 = quotient 3, remainder -6.

   This rule is known as truncating division, but some languages use different approaches such as floored division, rounded division, or Euclidean division. Wikipedia has details. ↩

7. The signed overflow condition is slightly stricter than necessary. For a word division, the 16-bit quotient is restricted to the range -32767 to 32767. However, a 16-bit signed value can take on the values -32768 to 32767. Thus, a quotient of -32768 fits in a 16-bit signed value even though the 8086 considers it an error. This is a consequence of the 8086 performing unsigned division and then updating the sign if necessary. ↩

8. The internal F1 flag is also used to keep track of a REP prefix for use with a string operation. I discussed string operations and the F1 flag in this post. ↩

9. Curiously, the 8086 patent states that the X register is a 4-bit register holding bits 3–6 of the byte (col. 9, line 20). But looking at the die, it is a 3-bit register holding bits 3–5 of the byte. ↩

10. Some instructions are specified by bits 5–3 in the ModR/M byte rather than in the first opcode byte. The motivation is to avoid wasting bits for instructions that use a ModR/M byte but don't need a register specification. For instance, consider the instruction ADD [BX],0x1234. This instruction uses a ModR/M byte to specify the memory address. However, because it uses an immediate operand, it does not need the register specification normally provided by bits 5–3 of the ModR/M byte. This frees up the bits to specify the instruction. From one perspective, this is an ugly hack, while from another perspective it is a clever optimization. ↩

11. Even the earliest computers such as ENIAC (1945) usually supported multiplication and division. However, early microprocessors did not provide multiplication and division instructions due to the complexity of these instructions. Instead, the programmer would need to write an assembly code loop, which was very slow. Early microprocessors often had binary-coded decimal instructions that could perform additions and subtractions in decimal. One motivation for these instructions was that converting between binary and decimal was extremely slow due to the need for multiplication and division. Instead, it was easier and faster to keep the values as decimal if that was how they were displayed.

    The Texas Instruments TMS9900 (1976) was one of the first microprocessors with multiplication and division instructions. Multiply and divide instructions remained somewhat controversial on RISC (Reduced Instruction-Set Computer) processors due to the complexity of these instructions. The early ARM processors, for instance, did not support multiplication and division. Multiplication was added to ARMv2 (1986) but most ARM processors still don't have integer division. The popular open-source RISC-V architecture (2015) doesn't include integer multiply and divide by default, but provides them as an optional "M" extension.

    The 8086's algorithm is designed for simplicity rather than speed. It is a "restoring" algorithm that checks before subtracting to ensure that the current term is always positive. This can require two ALU operations (comparison and subtraction) per cycle. A slightly more complex approach is a "nonrestoring" algorithm that subtracts even if it yields a negative term, and then adds during a later loop iteration. ↩

The microcode and hardware in the 8086 processor that perform string operations

Intel introduced the 8086 microprocessor in 1978. This processor ended up being hugely influential, setting the path for the x86 architecture that is extensively used today. One interesting feature of the 8086 was instructions that can efficiently operate on blocks of memory up to 64K bytes long.1 These instructions rapidly copy, compare, or scan data and are known as "string" instructions.2

In this blog post, I explain string operations in the 8086, analyze the microcode that it used, and discuss the hardware circuitry that helped it out. My analysis is based on reverse-engineering the 8086 from die photos. The photo below shows the chip under a microscope. I've labeled the key functional blocks; the ones that are important to this post are darker. Architecturally, the chip is partitioned into a Bus Interface Unit (BIU) at the top and an Execution Unit (EU) below. The BIU handles memory accesses, while the Execution Unit (EU) executes instructions. The microcode ROM at the lower right controls the process.

The 8086 die under a microscope, with main functional blocks labeled. This photo shows the chip with the metal and polysilicon removed, revealing the silicon underneath. Click on this image (or any other) for a larger version.

Segments and addressing

Before I get into the details of the string instructions, I need to give a bit of background on how the 8086 accesses memory through segments. Earlier microprocessors such as the Intel 8080 (1974) used 16 bits to specify a memory address, allowing a maximum of 64K of memory. This memory capacity is absurdly small by modern standards, but at the time when a 4K memory board cost hundreds of dollars, this limit was not a problem. However, due to Moore's Law and the exponential growth in memory capacity, the follow-on 8086 processor needed to support more memory. At the same time, the 8086 needed to use 16-bit registers for backward compatibility with the 8080.

The much-reviled solution was to create a 1-megabyte (20-bit) address space consisting of 64K segments, with a 16-bit address specifying a position within the segment. In more detail, the memory address was specified by a 16-bit offset address along with a particular 16-bit segment register selecting a segment. The segment register's value was shifted by 4 bits to give the segment's 20-bit base address. The 16-bit offset address was added, yielding a 20-bit memory address. This gave the processor a 1-megabyte address space, although only 64K could be accessed without changing a segment register. The 8086 had four segment registers so it could use multiple segments at the same time: the Code Segment, Data Segment, Stack Segment, and Extra Segment.

The 8086 chip is split into two processing units: the Bus Interface Unit (BIU) that handles segments and memory accesses, and the Execution Unit (EU) that executes instructions. The Execution Unit is what comes to mind when you think of a processor: it has most of the registers, the arithmetic/logic unit (ALU), and the microcode that implements instructions. The Bus Interface Unit interacts with memory and other external systems, performing the steps necessary to read and write memory.

Among other things, the Bus Interface Unit has a separate adder for address calculation; this adds the segment register to the base address to determine the final memory address. Every memory access uses the address adder at least once to add the segment base and offset. The address adder is also used to increment the program counter. Finally, the address adder increments and decrements the index registers used for block operations. This will be discussed in more detail below.

Microcode in the 8086

Most people think of machine instructions as the basic steps that a computer performs. However, many processors (including the 8086) have another layer of software underneath: microcode. With microcode, instead of building the control circuitry from complex logic gates, the control logic is largely replaced with code. To execute a machine instruction, the computer internally executes several simpler micro-instructions, specified by the microcode. This provides a considerable performance improvement for the block operations, which requires many steps in a loop. Performing this loop in microcode is considerably faster than writing the loop in assembly code.

A micro-instruction in the 8086 is encoded into 21 bits as shown below. Every micro-instruction specifies a move operation from a source register to a destination register, each specified with 5 bits. The meaning of the remaining bits depends on the type field and can be anything from an ALU operation to a memory read or write to a change of microcode control flow. Thus, an 8086 micro-instruction typically does two things in parallel: the move and the action. For more about 8086 microcode, see my microcode blog post.

The encoding of a micro-instruction into 21 bits. Based on NEC v. Intel: Will Hardware Be Drawn into the Black Hole of Copyright?

I'll explain the behavior of an ALU micro-operation since it is important for string operations. The Arithmetic/Logic Unit (ALU) is the heart of the processor, performing addition, subtraction, and logical operations. The ALU has three temporary input registers that are invisible to the programmer: tmpA, tmpB, and tmpC. An ALU operation takes its first argument from any temporary register, while the second argument always comes from tmpB. Performing an ALU operation requires two micro-instructions. The first micro-instruction specifies the ALU operation and source register, configuring the ALU. For instance, ADD tmpA configures the ALU to add the tmpA register to the default tmpB register. In the next micro-instruction (or a later one), the ALU result can be accessed through a special register called Σ (SIGMA) and moved to another register.

I'll also explain the memory read and write micro-operations. A memory operation uses two internal registers: IND (Indirect) holds the memory address, while OPR (Operand) holds the word that is read or written. A typical memory micro-instruction for a read is R DS,BL. This causes the Bus Interface Unit to compute the memory address by adding the Data Segment (DS) to the IND register and then perform the read. The Bus Interface Unit determines if the instruction is performing a byte operation or a word operation and reads a byte or word as appropriate, going through the necessary bus cycles. The BL option3 causes the Bus Interface Unit to update the IND register as appropriate,3 incrementing or decrementing it by 1 or 2 depending on the Direction Flag and the size of the access (byte or word). All of this complexity happens in the hardware of the Bus Interface Unit and is invisible to the microcode. The tradeoff is that this simplifies the microcode but makes the chip's hardware considerably more complicated.

The string move instruction

The 8086 has five types of string instructions, operating on blocks of memory: MOVS (Move String), CMPS (Compare Strings), SCAS (Scan String), LODS (Load String), and STOS (Store String). Each instruction operates on a byte or word, but by using a REP prefix, the operation can be repeated for up to 64k bytes, controlled by a counter. Conditional repetitions can terminate the loop on various conditions. The string instructions provide a flexible way to operate on blocks of memory, much faster than a loop written in assembly code.

The MOVS (Move String) operation copies one memory region to another. The CMPS (Compare Strings) operation compares two memory blocks and sets the status flags. In particular, this indicates if one string is greater, less, or equal to the other. The SCAS (Scan String) operation scans memory, looking for a particular value. The LODS (Load String) operation moves an element into the accumulator, generally as part of a more complex loop. Finally, STOS (Store String) stores the accumulator value, either to initialize a block of memory or as part of a more complex loop.4

Like many 8086 instructions, each string instruction has two opcodes: one that operates on bytes and one that operates on words. One of the interesting features of the 8086 is that the same microcode implements the byte and word instructions, while the hardware takes care of the byte- or word-sized operations as needed. Another interesting feature of the string operations is that they can go forward through memory, incrementing the pointers, or they can go backward, decrementing the points. A special processor flag, the Direction Flag, indicates the direction: 0 for incrementing and 1 for decrementing. Thus, there are four possibilities for stepping through memory, part of the flexibility of the string operations.

The flowchart below shows the complexity of these instructions. I'm not going to explain the flowchart at this point, but the point is that there is a lot going on. This functionality is implemented by the microcode.

This flowchart shows the operation of a string instruction. From The 8086 Family Users Manual, fig 2-33.

I'll start by explaining the MOVS (Move String) instruction, which moves (copies) a block of memory. Before executing this instruction, the registers should be configured so the SI Source Index register points to the first block, the DI Destination Index register points to the second block, and the CX Count register holds the number of bytes or words to move. The basic action of the MOVS instruction reads a byte (or word) from the SI address and updates SI, writes the value to the DI address and updates DI, and decrements the CX counter.

The microcode block below is executed for the MOVS (and LODS) instructions. There's a lot happening in this microcode with a variety of control paths, so it's a bit tricky to understand, but let's see how it goes. Each micro-instruction has a register-to-register move on the left and an action on the right, happening in parallel. The first micro-instruction handles the REP prefix, if any; let's assume for now that there's no prefix so it is skipped. Next is the read from memory, which requires the memory address to be in the IND register. Thus, the micro-instruction moves SI to IND and starts the read cycle (R DS,BL). When the read completes, the updated IND register is moved back to SI, updating that register. Meanwhile, X0 tests the opcode and jumps to "8" for LODS. The MOVS path falls through, getting the address from the DI register and writing to memory the value that we just read. The updated IND register is moved to DI while another conditional jump goes to "7" if there's no REP prefix. Micro-instruction 7 performs an RNI (Run Next Instruction), which ends the microcode and causes the next machine instruction to be decoded. As you can see, microcode is very low-level.

 move       action           
           CALL F1 RPTS MOVS/LODS: handle REP if active
SI → IND   R DS,BL      1: Read byte/word from SI
IND → SI   JMPS X0 8     test instruction bit 3: jump if LODS
DI → IND   W DA,BL       MOVS path: write to DI
IND → DI   JMPS NF1 7   4: run next instruction if not REP
Σ → tmpC   JMP INT RPTI 5: handle any interrupt
tmpC → CX  JMPS NZ 1     update CX, loop if not zero
           RNI          7: run next instruction

OPR → M    JMPS F1 5    8: LODS path: store AL/AX, jump back if REP
           RNI           run next instruction

Now let's look at the case with a REP prefix, causing the instruction to loop. The first step is to test if the count register CX is zero, and bail out of the loop if so. In more detail, the REP prefix sets an internal flag called F1. The first micro-instruction for MOVS above conditionally calls the RPTS subroutine if F1 is set. The RPTS subroutine below is a bit tricky. First, it moves the count in CX to the ALU's temporary C register. It also configures the ALU to pass tmpC through unchanged. The next move discards the ALU result Σ, but as a side effect, sets a flag if the value is zero. This micro-instruction also configures the ALU to perform DEC tmpC, but the decrement doesn't happen yet. Next, if the value is nonzero (NZ), the microcode execution jumps to 10 and returns from the microcode subroutine, continuing execution of the MOVS code described above. On the other hand, if CX is zero, execution falls through to RNI (Run Next Instruction), which terminates execution of the MOVS instruction.

CX → tmpC     PASS tmpC   RPTS: test CX
Σ → no dest   DEC tmpC     Set up decrement for later
              JMPS NZ 10   Jump to 10 if CX not zero
              RNI          If 0, run next instruction
              RTN         10: return

If execution returns to the MOVS microcode, it will execute as described earlier until the NF1 test below. With a REP prefix, the test fails and microcode execution falls through. The next micro-instruction performs Σ → tmpC, which puts the ALU result into tmpC. The ALU was configured back in the RPTS subroutine to decrement tmpC, which holds the count from CX, so the result is that CX is decremented, put into tmpC, and then put back into CX in the next micro-instruction. It seems like a roundabout way to decrement the counter, but that's microcode. Finally, if the value is nonzero (NZ), microcode execution jumps back to 1 (near the top of the MOVS code earlier), repeating the whole process. Otherwise, RNI ends processing of the instruction. Thus, the MOVS instruction repeats until CX is zero. In the next section, I'll explain how JMP INT RPTI handles an interrupt.

IND → DI   JMPS NF1 7   4: run next instruction if not REP
Σ → tmpC   JMP INT RPTI 5: handle any interrupt
tmpC → CX  JMPS NZ 1     update CX, loop if not zero
           RNI          7: run next instruction

The NZ (not zero) condition tests a special 16-bit zero flag, not the standard zero status flag. This allows zero to be tested without messing up the zero status flag.

Interrupts

Interrupts pose a problem for the string operations. The idea behind interrupts is that the computer can be interrupted during processing to handle a high-priority task, such as an I/O device that needs servicing. The processor stops its current task, executes the interrupt handling code, and then returns to the original task. The 8086 processor normally completes the instruction that it is executing before handling the interrupt, so it can continue from a well-defined state. However, a string operation can perform up to 64k moves, which could take a large fraction of a second.5 If the 8086 waited for the string operation to complete, interrupt handling would be way too slow and could lose network packets or disk data, for instance.

The solution is that a string instruction can be interrupted in the middle of the instruction, unlike most instructions. The string instructions are designed to use registers in a way that allows the instruction to be restarted. The idea is that the CX register holds the current count, while the SI and DI registers hold the current memory pointers, and these registers are updated as the instruction progresses. If the instruction is interrupted it can simply continue where it left off. After the interrupt, the 8086 restarts the string operation by backing the program counter up by two bytes (one byte for the REP prefix and one byte for the string opcode.) This causes the interrupted string operation to be re-executed, continuing where it left off.

If there is an interrupt, the RPTI microcode routine below is called to update the program counter. Updating the program counter is harder than you'd expect because the 8086 prefetches instructions. The idea is that while the memory bus is idle, instructions are read from memory into a prefetch queue. Then, when an instruction is needed, the processor can (hopefully) get the instruction immediately from the prefetch queue instead of waiting for a memory access. As a result, the program counter in the 8086 points to the memory address of the next instruction to fetch, not the next instruction to execute. To get the "real" program counter value, prefetching is first suspended (SUSP). Then the PC value is corrected (CORR) by subtracting the length of the prefetch queue. At this point, the PC points to the next instruction to execute.

tmpC → CX   SUSP        RPTI: store CX
            CORR         correct PC
PC → tmpB   DEC2 tmpB  
Σ → PC      FLUSH RNI    PC -= 2, end instruction

At last, the microcode gets to the purpose of this subroutine: the PC is decremented by 2 (DEC2) using the ALU. The prefetch queue is flushed and restarted and the RNI micro-operation terminates the microcode and runs the next instruction. Normally this would execute the instruction from the new program counter value (which now points to the string operation). However, since there is an interrupt pending, the interrupt will take place instead, and the interrupt handler will execute. After the interrupt handler finishes, the interrupted string operation will be re-executed, continuing where it left off.

There's another complication, of course. An 8086 instruction can have multiple prefixes attached, for example using a segment register prefix to access a different segment. The approach of backing up two bytes will only execute the last prefix, ignoring any others, so if you have two prefixes, the instruction doesn't get restarted correctly. The 8086 documentation describes this unfortunate behavior. Apparently a comprehensive solution (e.g. counting the prefixes or providing a buffer to hold prefixes during an interrupt) was impractical for the 8086. I think this was fixed in the 80286.

The remaining string instructions

I'll discuss the microcode for the other string operations briefly. The LODS instruction loads from memory into the accumulator. It uses the same microcode routine as MOVS; the code below is the same code discussed earlier. However, the path through the microcode is different for LODS since the JMPS X0 8 conditional jump will be taken. (This tests bit 3 of the opcode, which is set for LODS.) At step 8, a value has been read from memory and is in the OPR (Operand) register. This micro-instruction moves the value from OPR to the accumulator (represented by M for complicated reasons6). If there is a repeat prefix, the microcode jumps back to the previous flow (5). Otherwise, RNI runs the next instruction. Thus, LODS shares almost all its microcode with MOVS, making the microcode more compact at the cost of slowing it down slightly due to the conditional jumps.

 move       action           
           CALL F1 RPTS MOVS/LODS: handle REP if active
SI → IND   R DS,BL      1: Read byte/word from SI
IND → SI   JMPS X0 8     test instruction bit 3: jump if LODS
DI → IND   W DA,BL       MOVS path: write to DI
IND → DI   JMPS NF1 7   4: run next instruction if not REP
Σ → tmpC   JMP INT RPTI 5: handle any interrupt
tmpC → CX  JMPS NZ 1     update CX, loop if not zero
           RNI          7: run next instruction

OPR → M    JMPS F1 5    8: LODS path: store AL/AX, jump back if REP
           RNI           run next instruction

The STOS instruction is the opposite of LODS, storing the accumulator value into memory. The microcode (below) is essentially the second half of the MOVS microcode. The memory address in DI is moved to the IND register and the value in the accumulator is moved to the OPR register to set up the write operation. (As with LODS, the M register indicates the accumulator.6) The CX register is decremented using the ALU.

DI → IND    CALL F1 RPTS   STOS: if REP prefix, test if done
M → OPR     W DA,BL        1: write the value to memory
IND → DI    JMPS NF1 5      Quit if not F1 (repeat)
Σ → tmpC    JMP INT RPTI    Jump to RPTI if interrupt
tmpC → CX   JMPS NZ 1       Loop back if CX not zero
            RNI            5: run next instruction

The CMPS instruction compares strings, while the SCAS instruction looks for a zero or non-zero value, depending on the prefix. They share the microcode routine below, with the X0 condition testing bit 3 of the instruction to select the path. The difference is that CMPS reads the comparison character from SI, while SCAS compares against the character in the accumulator. The comparison itself is done by subtracting the two values and discarding the result. The F bit in the micro-instruction causes the processor's status flags to be updated with the result of the subtraction, indicating less than, equal, or greater than.

            CALL F1 RPTS   CMPS/SCAS: if RPT, quit if done
M → tmpA    JMPS X0 5      1:accum to tmpA, jump if SCAS
SI → IND    R DS,BL         CMPS path, read from SI to tmpA
IND → SI                    update SI
OPR → tmpA                  fallthrough
DI → IND    R DA,BL        5: both: read from DI to tmpB
OPR → tmpB  SUBT tmpA       subtract to compare
Σ → no dest DEC tmpC F      update flags, set up DEC
IND → DI    JMPS NF1 12     return if not RPT
Σ → CX      JMPS F1ZZ 12    update CX, exit if condition
Σ → tmpC    JMP INT RPTI    if interrupt, jump to RPTI
            JMPS NZ 1       loop if CX ≠ 0
            RNI            12: run next instruction

One tricky part about the scan and compare instructions is that you can either repeat until the values are equal or until they are unequal, with the REPE or REPNE prefixes respectively. Rather than implementing this two-part condition in microcode, the F1ZZ condition above tests the right condition depending on the prefix.

Hardware support

Although the 8086 uses microcode to implement instructions, it also uses a considerable amount of hardware to simplify the microcode. This hybrid approach was necessary in order to fit the microcode into the small ROM capacity available in 1978.7 This section discusses some of the hardware circuitry in the 8086 that supports the string operations.

Implementing the REP prefixes

Instruction prefixes, including REPNZ and REPZ, are executed in hardware rather than microcode. The first step of instruction decoding, before microcode starts, is the Group Decode ROM. This ROM categorizes instructions into various groups. For instructions that are categorized as prefixes, the signal from the Group Decode ROM delays any interrupts (because you don't want an interrupt between the prefix and the instruction) and starts the next instruction without executing microcode. The Group Decode ROM also outputs a REP signal specifically for these two prefixes. This signal causes the F1 latch to be loaded with 1, indicating a REP prefix. (This latch is also used during multiplication to track the sign.) This signal also causes the F1Z latch to be loaded with bit 0 of the instruction, which is 0 for REPNZ and 1 for REPZ. The microcode uses these latches to determine the appropriate behavior of the string instruction.

Updating SI and DI: the Constant ROM

The SI and DI index registers are updated during each step to point to the next element. This update is more complicated than you might expect, though, since the registers are incremented or decremented based on the Direction Flag. Moreover, the step size, 1 or 2, varies for a byte or word operation. Another complication is unaligned word accesses, using an odd memory address to access a word. The 8086's bus can only handle aligned words, so an unaligned word access is split into two byte accesses, incrementing the address after the first access. If the operation is proceeding downward, the address then needs to be decremented by 3 (not 2) at the end to cancel out this increment. The point is that updating the index registers is not trivial but requires an adjustment anywhere between -3 and +2, depending on the circumstances.

The Bus Interface Unit performs these updates automatically, without requiring the microcode to implement the addition or subtraction. The arithmetic is not performed by the regular ALU (Arithmetic/Logic Unit) but by the special adder dedicated to addressing arithmetic. The increment or decrement value is supplied by a special ROM called the Constant ROM, located next to the adder. The Constant ROM (shown below) is implemented as a PLA (programmable logic array), a two-level structured arrangement of gates. The first level (bottom) selects the desired constant, while the second level (middle) generates the bits of the constant: three bits plus a sign bit. The constant ROM is also used for correcting the program counter value as described earlier.

The Constant ROM, highlighted on the die. The correction constants are used to correct the PC.

Condition testing

The microcode supports conditional jumps based on 16 conditions. Several of these conditions are designed to support the string operations. To test if a REP prefix is active, microcode uses the F1 test, which tests the F1 latch. The REPZ and REPNZ prefixes loop while the zero flag is 1 or 0 respectively. This somewhat complicated test is supported in microcode by the F1ZZ condition, which evaluates the zero flag XOR the F1Z latch. Thus, it tests for zero with REPZ (F1Z=0) and nonzero with REPNZ (F1Z=1).

Looping happens as long as the CX register is nonzero. This is tested in microcode with the NZ (Not Zero) condition. A bit surprisingly, this test doesn't use the standard zero status flag, but a separate latch that tracks if an ALU result is zero. (I call this the Z16 flag since it tests the 16-bit value, unlike the regular zero flag which tests either a byte or word.) The Z16 flag is only used by the microcode and is invisible to the programmer. The motivation behind this separate flag is so the string operations can leave the visible zero flag unchanged.8

Another important conditional jump is X0, which tests bit 3 of the instruction. This condition distinguishes between the MOVS and LODS instructions, which differ in bit 3, and similarly for CMPS versus SCAS. The test uses the X register which stores part of the instruction during decoding. Note that the opcodes aren't arbitrarily assigned to instructions like MOVS and LODS. Instead, the opcodes are carefully assigned so the instructions can share microcode but be distinguished by X0. Finally, the string operation microcode also uses the INT condition, which tests if an interrupt is pending.

The conditions are evaluated by the condition PLA (Programmable Logic Array, a grid of gates), shown below. The four condition bits from the micro-instruction, along with their complements, are fed into the columns. The PLA has 16 rows, one for each condition. Each row is a NOR gate matching one bit combination (i.e. selecting a condition) and the corresponding signal value to test. Thus, if a particular condition is specified and is satisfied, that row will be 1. The 16 row outputs are combined by the 16-input NOR gate at the left. Thus, if the specified condition is satisfied, this output will be 0, and if the condition is unsatisfied, the output will be 1. This signal controls the jump or call micro-instruction: if the condition is satisfied, the new micro-address is loaded into the microcode address register. If the condition is not satisfied, the microcode proceeds sequentially. I discuss the 8086's conditional circuitry in more detail in this post.

The condition PLA evaluates microcode conditionals.

Conclusions

Hopefully you have found this close examination of microcode interesting. Microcode is implemented at an even lower level than assembly code, so it can be hard to understand. Moreover, the microcode in the 8086 was carefully optimized to make it compact, so it is even more obscure.

One of the big computer architecture debates of the 1980s was "RISC vs CISC", pitting Reduced Instruction Set Computers against Complex Instruction Set Computers. Looking at the 8086 in detail has given me more appreciation for the issues in a CISC processor such as the 8086. The 8086's string instructions are an example of the complex instructions in the 8086 that reduced the "semantic gap" between assembly code and high-level languages and minimized code size. While these instructions are powerful, their complexity spreads through the chip, requiring additional hardware features described above. These instructions also caused a great deal of complications for interrupt handling, including prefix-handling bugs that weren't fixed until later processors.

I've written multiple posts on the 8086 so far and plan to continue reverse-engineering the 8086 die so follow me on Twitter @kenshirriff or RSS for updates. I've also started experimenting with Mastodon recently as @[email protected].

Notes and references

1. Block move instructions didn't originate with the 8086. The IBM System/360 series of mainframes had an extensive set of block instructions providing moves, compare, logical operations (AND, OR, Exclusive OR), character translation, formatting, and decimal arithmetic. These operations supported blocks of up to 256 characters.

   The Z80 processor (1976) had block instructions to move and compare blocks of data. The Z80 supported ascending and descending movements, but used separate instructions instead of a direction flag like the 8086. ↩

2. The "string" operations process arbitrary memory bytes or words. Despite the name, these instructions are not specific to zero-terminated strings or any other string format. ↩

3. The BL value in the micro-instruction indicates that the IND register should be incremented or decremented by 1 or 2 as appropriate. I'm not sure what BL stands for in the microcode. The patent says "BL symbolically represents a two bit code which causes external logic to examine the byte or word line and the direction flag in PSW register to generate, according to random logic well known to the art, the address factor required." So perhaps "Byte Logic"? ↩↩

4. The designer of the 8086 instruction set, Steve Morse, discusses the motivation behind the string operations in his book The 8086/8088 primer. These instructions were designed to be flexible and support a variety of use cases. The XLAT (Translate) and JCXZ (Jump if CX Zero) instructions were designed to work well with the string instructions.

   The implementation of string instructions is discussed in detail in the 8086 patent, section 13 onward. ↩

5. A string operation could perform 64k moves, each of which consists of a read and a write, yielding 128k memory operations. I think that if the memory accesses are unaligned, i.e. a word access to an odd address, then each byte of the word needs to be accessed separately. So I think you could get up to 256k memory accesses. Each memory operation takes at least 4 clock cycles, more if the memory is slow and has wait states. So one string instruction could take over a million clock cycles. ↩

6. You might wonder why the register M indicates the accumulator, and the explanation is a bit tricky. The microcode uses 5-bit register specifications to indicate the source and destination for a data move. Registers can be specified explicitly, such as AX or BX, or a byte register such as AL or an internal register such as IND or tmpA. However, the microcode can also specify a generic source or destination register with M or N. The motivation is that the 8086 has a lot of operations that use an arbitrary source and destination register, for instance ADD AX, BX. Rather than making the microcode figure out which registers to use for these instructions, the hardware decodes the register fields from the instruction and substitutes the appropriate registers for M and N. This makes the microcode much simpler.

   But why does the LODS microcode use the M register instead of AX when this instruction only works with the accumulator? The microcode takes advantage of another clever feature of the M and N registers. The hardware looks at the instruction to determine if it is a byte or word instruction, and performs an 8-bit or 16-bit transfer accordingly. If the LODS microcode was hardcoded for the accumulator, the microcode would need separate paths for AX and AL, the full accumulator and the lower byte of the accumulator.

   The final piece of the puzzle is how the hardware knows to use the accumulator for the string instructions when they don't explicitly specify a register. The first step of instruction decoding is the Group Decode ROM, which categorizes instructions into various groups. One group is "instructions that use the accumulator". The string operations are categorized in this group, which causes the hardware to use the accumulator when the M register is specified. (Other instructions in this group include the immediate ALU operations, I/O operations, and accumulator moves.)

   I discussed the 8086's register codes in more detail here. ↩↩

7. The 8086's microcode ROM was small: 512 words of 21 bits. In comparison, the VAX 11/780 minicomputer (1977) had 5120 words of 96 bits, over 45 times as large. ↩

8. The internal Z16 zero flag is mostly used by the string operations. It is also used by the LOOP iteration-control instructions and the shift instructions that take a shift count. ↩

Reverse-engineering the Globus INK, a Soviet spaceflight navigation computer

One of the most interesting navigation instruments onboard Soyuz spacecraft was the Globus INK,1 which used a rotating globe to indicate the spacecraft's position above the Earth. This electromechanical analog computer used an elaborate system of gears, cams, and differentials to compute the spacecraft's position. The globe rotates in two dimensions: it spins end-over-end to indicate the spacecraft's orbit, while the globe's hemispheres rotate according to the Earth's daily rotation around its axis.2 The spacecraft's position above the Earth was represented by the fixed crosshairs on the plastic dome. The Globus also has latitude and longitude dials next to the globe to show the position numerically, while the light/shadow dial below the globe indicated when the spacecraft would enter or leave the Earth's shadow.

The INK-2S "Globus" space navigation indicator.

Opening up the Globus reveals that it is packed with complicated gears and mechanisms. It's amazing that this mechanical technology was used from the 1960s into the 21st century. But what are all those gears doing? How can orbital functions be implemented with gears? To answer these questions, I reverse-engineered the Globus and traced out its system of gears.

The Globus with the case removed, showing the complex gearing inside.

The diagram below summarizes my analysis. The Globus is an analog computer that represents values by rotating shafts by particular amounts. These rotations control the globe and the indicator dials. The flow of these rotational signals is shown by the lines on the diagram. The computation is based around addition, performed by ten differential gear assemblies. On the diagram, each "⨁" symbol indicates one of these differential gear assemblies. Other gears connect the components while scaling the signals through various gear ratios. Complicated functions are implemented with three specially-shaped cams. In the remainder of this blog post, I will break this diagram down into functional blocks and explain how the Globus operates.

This diagram shows the interconnections of the gear network in the Globus.

For all its complexity, though, the functionality of the Globus is pretty limited. It only handles a fixed orbit at a specific angle, and treats the orbit as circular. The Globus does not have any navigation input such as an inertial measurement unit (IMU). Instead, the cosmonauts configured the Globus by turning knobs to set the spacecraft's initial position and orbital period. From there, the Globus simply projected the current position of the spacecraft forward, essentially dead reckoning.

A closeup of the gears inside the Globus.

The globe

On seeing the Globus, one might wonder how the globe is rotated. It may seem that the globe must be free-floating so it can rotate in two axes. Instead, a clever mechanism attaches the globe to the unit. The key is that the globe's equator is a solid piece of metal that rotates around the horizontal axis of the unit. A second gear mechanism inside the globe rotates the globe around the North-South axis. The two rotations are controlled by concentric shafts that are fixed to the unit. Thus, the globe has two rotational degrees of freedom, even though it is attached at both ends.

The photo below shows the frame that holds and controls the globe. The dotted axis is fixed horizontally in the unit and rotations are fed through the two gears at the left. One gear rotates the globe and frame around the dotted axis, while the gear train causes the globe to rotate around the vertical polar axis (while the equator remains fixed).

The axis of the globe is at 51.8° to support that orbital inclination.

The angle above is 51.8° which is very important: this is the inclination of the standard Soyuz orbit. As a result, simply rotating the globe around the dotted line causes the crosshair to trace the orbit.3 Rotating the two halves of the globe around the poles yields the different paths over the Earth's surface as the Earth rotates. An important consequence of this design is that the Globus only supports a circular orbit at a fixed angle.

Differential gear mechanism

The primary mathematical element of the Globus is the differential gear mechanism, which can perform addition or subtraction. A differential gear takes two rotations as inputs and produces the (scaled) sum of the rotations as the output. The photo below shows one of the differential mechanisms. In the middle, the spider gear assembly (red box) consists of two bevel gears that can spin freely on a vertical shaft. The spider gear assembly as a whole is attached to a horizontal shaft, called the spider shaft. At the right, the spider shaft is attached to a spur gear (a gear with straight-cut teeth). The spider gear assembly, the spider shaft, and the spider's spur gear rotate together as a unit.

Diagram showing the components of a differential gear mechanism.

At the left and right are two end gear assemblies (yellow). The end gear is a bevel gear with angled teeth to mesh with the spider gears. Each end gear is locked to a spur gear and these gears spin freely on the horizontal spider shaft. In total, there are three spur gears: two connected to the end gears and one connected to the spider assembly. In the diagrams, I'll use the symbol below to represent the differential gear assembly: the end gears are symmetric on the top and bottom, with the spider shaft on the side. Any of the three spur gears can be used as an output, with the other two serving as inputs.

The symbol for the differential gear assembly.

To understand the behavior of the differential, suppose the two end gears are driven in the same direction at the same rate, say upwards.4 These gears will push on the spider gears and rotate the spider gear assembly, with the entire differential rotating as a fixed unit. On the other hand, suppose the two end gears are driven in opposite directions. In this case, the spider gears will spin on their shaft, but the spider gear assembly will remain stationary. In either case, the spider gear assembly motion is the average of the two end gear rotations, that is, the sum of the two rotations divided by 2. (I'll ignore the factor of 2 since I'm ignoring all the gear ratios.) If the operation of the differential is still confusing, this vintage Navy video has a detailed explanation.

The controls and displays

The diagram below shows the controls and displays of the Globus. The rotating globe is the centerpiece of the unit. Its plastic cover has a crosshair that represents the spacecraft's position above the Earth's surface. Surrounding the globe itself are dials that show the longitude, latitude, and the time before entering light and shadow. The cosmonauts manually initialize the globe position with the concentric globe rotation knobs: one rotates the globe along the orbital path while the other rotates the hemispheres. The mode switch at the top selects between the landing position mode, the standard Earth orbit mode, and turning off the unit. The orbit time adjustment configures the orbital time period in minutes while the orbit counter below it counts the number of orbits. Finally, the landing point angle sets the distance to the landing point in degrees of orbit.

The Globus with the controls labeled.

Computing the orbit time

The primary motion of the Globus is the end-over-end rotation of the globe showing the movement of the spacecraft in orbit. The orbital motion is powered by a solenoid at the top of the Globus that receives pulses once a second and advances a ratchet wheel (video).5 This wheel is connected to a complicated cam and differential system to provide the orbital motion.

The orbit solenoid (green) has a ratchet that rotates the gear to the right. The shaft connects it to differential gear assembly 1 at the bottom right.

Each orbit takes about 92 minutes, but the orbital time can be adjusted by a few minutes in steps of 0.01 minutes6 to account for changes in altitude. The Globus is surprisingly inflexible and this is the only orbital parameter that can be adjusted.7 The orbital period is adjusted by the three-position orbit time switch, which points to the minutes, tenths, or hundredths. Turning the central knob adjusts the indicated period dial.

The problem is how to generate the variable orbital rotation speed from the fixed speed of the solenoid. The solution is a special cam, shaped like a cone with a spiral cross-section. Three followers ride on the cam, so as the cam rotates, the follower is pushed outward and rotates on its shaft. If the follower is near the narrow part of the cam, it moves over a small distance and has a small rotation. But if the follower is near the wide part of the cam, it moves a larger distance and has a larger rotation. Thus, by moving the follower to a particular point on the cam, the rotational speed of the follower is selected. One follower adjusts the speed based on the minutes setting with others for the tenths and hundredths of minutes.

A diagram showing the orbital speed control mechanism. The cone has three followers, but only two are visible from this angle. The "transmission" gears are moved in and out by the outer knob to select which follower is adjusted by the inner knob.

Of course, the cam can't spiral out forever. Instead, at the end of one revolution, its cross-section drops back sharply to the starting diameter. This causes the follower to snap back to its original position. To prevent this from jerking the globe backward, the follower is connected to the differential gearing via a slip clutch and ratchet. Thus, when the follower snaps back, the ratchet holds the drive shaft stationary. The drive shaft then continues its rotation as the follower starts cycling out again. Each shaft output is accordingly a (mostly) smooth rotation at a speed that depends on the position of the follower.

A cam-based system adjusts the orbital speed using three differential gear assemblies.

The three adjustment signals are scaled by gear ratios to provide the appropriate contribution to the rotation. As shown above, the adjustments are added to the solenoid output by three differentials to generate the orbit rotation signal, output from differential 3.8 This signal also drives the odometer-like orbit counter on the front of the Globus. The diagram below shows how the components are arranged, as viewed from the back.

A back view of the Globus showing the orbit components.

Displaying the orbit rotation

Since the Globus doesn't have any external position input such as inertial guidance, it must be initialized by the cosmonauts. A knob on the front of the Globus provides manual adjustment of the orbital position. Differential 4 adds the knob signal to the orbit output discussed above.

The orbit controls drive the globe's motion.

The Globus has a "landing point" mode where the globe is rapidly rotated through a fraction of an orbit to indicate where the spacecraft would land if the retro-rockets were fired. Turning the mode switch caused the globe to rotate until the landing position was under the crosshairs and the cosmonauts could evaluate the suitability of this landing site. This mode is implemented with a landing position motor that provides the rapid rotation. This motor also rotates the globe back to the orbital position. The motor is driven through an electronics board with relays and a transistor, controlled by limit switches. I discussed the electronics in a previous post so I won't go into more details here. The landing position motor feeds into the orbit signal through differential 5, producing the final orbit signal.

The landing position motor and its associated gearing. The motor speed is geared down and then fed through a worm gear (upper center).

The orbit signal from differential 5 is used in several ways. Most importantly, the orbit signal provides the end-over-end rotation of the globe to indicate the spacecraft's travel in orbit. As discussed earlier, this is accomplished by rotating the globe's metal frame around the horizontal axis. The orbital signal also rotates a potentiometer to provide an electrical indication of the orbital position to other spacecraft systems.

The light/shadow indicator

Docking a spacecraft is a tricky endeavor, best performed in daylight, so it is useful to know how much time remains until the spacecraft enters the Earth's shadow. The light/shadow dial under the globe provides this information. This display consists of two nested wheels. The outer wheel is white and has two quarters removed. Through these gaps, the partially-black inner wheel is exposed, which can be adjusted to show 0% to 50% dark. This display is rotated by the orbital signal, turning half a revolution per orbit. As the spacecraft orbits, this dial shows the light/shadow transition and the time to the transistion.9

The light/shadow indicator, viewed from the underside of the Globus. The shadow indicator has been set to 35% shadow. Near the hub, a pin restricts motion of the inner wheel relative to the outer wheel.

You might expect the orbit to be in the dark 50% of the time, but because the spacecraft is about 200 km above the Earth's surface, it will sometimes be illuminated when the surface of the Earth underneath is dark.10 In the ground track below, the dotted part of the track is where the spacecraft is in the Earth's shadow; this is considerably less than 50%. Also note that the end of the orbit doesn't match up with the beginning, due to the Earth's rotation during the orbit.

Ground track of an Apollo-Soyuz Test Project orbit, corresponding to this Globus. Image courtesy of heavens-above.com.

The latitude indicator

The latitude indicator to the left of the globe shows the spacecraft's latitude. The map above shows how the latitude oscillates between 51.8°N and 51.8°S, corresponding to the launch inclination angle. Even though the path around the globe is a straight (circular) line, the orbit appears roughly sinusoidal when projected onto the map.11 The exact latitude is a surprisingly complicated function of the orbital position.12 This function is implemented by a cam that is attached to the globe. The varying radius of the cam corresponds to the function. A follower tracks the profile of the cam and rotates the latitude display wheel accordingly, providing the non-linear motion.

A cam is attached to the globe and rotates with the globe.

The Earth's rotation

The second motion of the globe is the Earth's daily rotation around its axis, which I'll call the Earth rotation. The Earth rotation is fed into the globe through the outer part of a concentric shaft, while the orbital rotation is provided through the inner shaft. The Earth rotation is transferred through three gears to the equatorial frame, where an internal mechanism rotates the hemispheres. There's a complication, though: if the globe's orbital shaft turns while the Earth rotation shaft remains stationary, the frame will rotate, causing the gears to turn and the hemispheres to rotate. In other words, keeping the hemispheres stationary requires the Earth shaft to rotate with the orbit shaft.

A closeup of the gear mechanisms that drive the Globus, showing the concentric shafts that control the two rotations.

The Globus solves this problem by adding the orbit rotation to the Earth rotation, as shown in the diagram below, using differentials 7 and 8. Differential 8 adds the normal orbit rotation, while differential 7 adds the orbit rotation due to the landing motor.14

The mechanism to compute the Earth's rotation around its axis.

The Earth motion is generated by a second solenoid (below) that is driven with one pulse per second.13 This motion is simpler than the orbit motion because it has a fixed rate. The "Earth" knob on the front of the Globus permits manual rotation around the Earth's axis. This signal is combined with the solenoid signal by differential 6. The sum from the three differentials is fed into the globe, rotating the hemispheres around their axis.

This solenoid, ratchet, and gear on the underside of the Globus drive the Earth rotation.

The solenoid and differentials are visible from the underside of the Globus. The diagram below labels these components as well as other important components.

The underside of the Globus.

The longitude display

The longitude cam and the followers that track its radius.

The longitude display is more complicated than the latitude display because it depends on both the Earth rotation and the orbit rotation. Unlike the latitude, the longitude doesn't oscillate but increases. The longitude increases by 360° every orbit according to a complicated formula describing the projection of the orbit onto the globe. Most of the time, the increase is small, but when crossing near the poles, the longitude changes rapidly. The Earth's rotation provides a smaller but steady negative change to the longitude.

The computation of the longitude.

The diagram above shows how the longitude is computed by combining the Earth rotation with the orbit rotation. Differential 9 adds the linear effect of the orbit on longitude (360° per orbit) and subtracts the effect of the Earth's rotation (360° per day). The nonlinear effect of the orbit is computed by a cam that is rotated by the orbit signal. The shape of the cam is picked up and fed into differential 10, computing the longitude that is displayed on the dial. The differentials, cam, and dial are visible from the back of the Globus (below).

A closeup of the differentials from the back of the Globus.

The time-lapse video below demonstrates the behavior of the rotating displays. The latitude display on the left oscillates between 51.8°N and 51.8°S. The longitude display at the top advances at a changing rate. Near the equator, it advances slowly, while it accelerates near the poles. The light/shadow display at the bottom rotates at a constant speed, completing half a revolution (one light/shadow cycle) per orbit.

Conclusions

The Globus INK is a remarkable piece of machinery, an analog computer that calculates orbits through an intricate system of gears, cams, and differentials. It provided astronauts with a high-resolution, full-color display of the spacecraft's position, way beyond what an electronic space computer could provide in the 1960s.

The drawback of the Globus is that its functionality is limited. Its parameters must be manually configured: the spacecraft's starting position, the orbital speed, the light/shadow regions, and the landing angle. It doesn't take any external guidance inputs, such as an IMU (inertial measurement unit), so it's not particularly accurate. Finally, it only supports a circular orbit at a fixed angle. While a more modern digital display lacks the physical charm of a rotating globe, the digital solution provides much more capability.

I recently wrote blog posts providing a Globus overview and the Globus electronics. Follow me on Twitter @kenshirriff or RSS for updates. I've also started experimenting with Mastodon recently as @[email protected]. Many thanks to Marcel for providing the Globus. I worked on this with CuriousMarc, so check out his Globus videos.

Notes and references

1. In Russian, the name for the device is "Индикатор Навигационный Космический" abbreviated as ИНК (INK). This translates to "space navigation indicator." but I'll use the more descriptive nickname "Globus" (i.e. globe). The Globus has a long history, back to the beginnings of Soviet crewed spaceflight. The first version was simpler and had the Russian acronym ИМП (IMP). Development of the IMP started in 1960 for the Vostok (1961) and Voshod (1964) spaceflights. The more complex INK model (described in this blog post) was created for the Soyuz flights, starting in 1967. The landing position feature is the main improvement of the INK model. The Soyuz-TMA (2002) upgraded to the Neptun-ME system which used digital display screens and abandoned the Globus. ↩

2. According to this document, one revolution of the globe relative to the axis of daily rotation occurs in a time equal to a sidereal day, taking into account the precession of the orbit relative to the earth's axis, caused by the asymmetry of the Earth's gravitational field. (A sidereal day is approximately 4 minutes shorter than a regular 24-hour day. The difference is that the sidereal day is relative to the fixed stars, rather than relative to the Sun.) ↩

3. To see how the angle between the poles and the globe's rotation results in the desired orbital inclination, consider two limit cases. First, suppose the angle between is 90°. In this case, the globe is "straight" with the equator horizontal. Rotating the globe along the horizontal axis, flipping the poles end-over-end, will cause the crosshair to trace a polar orbit, giving the expected inclination of 90°. On the other hand, suppose the angle is 0°. In this case, the globe is "sideways" with the equator vertical. Rotating the globe will cause the crosshair to remain over the equator, corresponding to an equatorial orbit with 0° inclination. ↩

4. There is a bit of ambiguity when describing the gear motions. If the end gears are rotating upwards when viewed from the front, the gears are both rotating clockwise when viewed from the right, so I'm referring to them as rotating in the same direction. But if you view each gear from its own side, the gear on the left is turning counterclockwise, so from that perspective they are turning in opposite directions. ↩

5. The solenoids are important since they provide all the energy to drive the globe. One of the problems with gear-driven analog computers is that each gear and shaft has a bit of friction and loses a bit of torque, and there is nothing to amplify the signal along the way. Thus, the 27-volt solenoids need to provide enough force to run the entire system. ↩

6. The orbital time can be adjusted between 86.85 minutes and 96.85 minutes according to this detailed page that describes the Globus in Russian. ↩

7. The Globus is manufactured for a particular orbital inclination, in this case 51.8°. The Globus assumes a circular orbit and does not account for any variations. The Globus does not account for any maneuvering in orbit. ↩

8. The outputs from the orbit cam are fed into the overall orbit rotation, which drives the orbit cam. This may seem like an "infinite loop" since the outputs from the cam turn the cam itself. However, the outputs from the cam are a small part of the overall orbit rotation, so the feedback dies off. ↩

9. The scales on the light/shadow display are a bit confusing. The inner scale (blue) is measured in percentage of an orbit, up to 100%. The fixed outer scale (red) measures minutes, indicating how many minutes until the spacecraft enters or leaves shadow. The spacecraft completes 100% of an orbit in about 90 minutes, so the scales almost, but not quite, line up. The wheel is driven by the orbit mechanism and turns half a revolution per orbit.

   

   The light and shadow indicator is controlled by two knobs.

    ↩

10. The Internation Space Station illustrates how an orbiting spacecraft is illuminated more than 50% of the time due to its height. You can often see the ISS illuminated in the nighttime sky close to sunset and sunrise (link). ↩

11. The ground track on the map is roughly, but not exactly, sinusoidal. As the orbit swings further from the equator, the track deviates more from a pure sinusoid. The shape will depend, of course, on the rectangular map projection. For more information, see this StackExcahnge post. ↩

12. To get an idea of how the latitude and longitude behave, consider a polar orbit with 90° angle of inclination, one that goes up a line of longitude, crosses the North Pole, and goes down the opposite line of latitude. Now, shift the orbit away from the poles a bit, but keeping a great circle. The spacecraft will go up, nearly along a constant line of longitude, with the latitude increasing steadily. As the spacecraft reaches the peak of its orbit near the North Pole, it will fall a bit short of the Pole but will still rapidly cross over to the other side. During this phase, the spacecraft rapidly crosses many lines of longitude (which are close together near the Pole) until it reaches the opposite line of longitude. Meanwhile, the latitude stops increasing short of 90° and then starts dropping. On the other side, the process repeats, with the longitude nearly constant while the latitude drops relatively constantly.

    The latitude and longitude are generated by complicated trigonometric functions. The latitude is given by arcsin(sin i * sin (2πt/T)), while the longitude is given by λ = arctan (cos i * tan(2πt/T)) + Ωt + λ₀, where t is the spaceship's flight time starting at the equator, i is the angle of inclination (51.8°), T is the orbital period, Ω is the angular velocity of the Earth's rotation, and λ₀ is the longitude of the ascending node. ↩

13. An important function of the gears is to scale the rotations as needed by using different gear ratios. For the most part, I'm ignoring the gear ratios, but the Earth rotation gearing is interesting. The gear driven by the solenoid has 60 teeth, so it rotates exactly once per minute. This gear drives a shaft with a very small gear on the other end with 15 teeth. This gear meshes with a much larger gear with approximately 75 teeth, which will thus rotate once every 5 minutes. The other end of that shaft has a gear with approximately 15 teeth, meshed with a large gear with approximately 90 teeth. This divides the rate by 6, yielding a rotation every 30 minutes. The sequence of gears and shafts continues, until the rotation is reduced to once per day. (The tooth counts are approximate because the gears are partially obstructed inside the Globus, making counting difficult.) ↩

14. There's a potential simplification when canceling out the orbital shaft rotation from the Earth rotation. If the orbit motion was taken from differential 5 instead of differential 4, the landing motor effect would get added automatically, eliminating the need for differential 7. I think the landing motor motion was added separately so the mechanism could account for the Earth's rotation during the landing descent. ↩