Talking with the Moon: Inside Apollo's premodulation processor

The Apollo missions to the Moon required complex hardware to communicate between Earth and the spacecraft, sending radio signals over hundreds of thousands of miles. The premodulation processor was a key component of this system, combining voice, scientific data, TV, and telemetry for transmission to Earth.1 It was built from components that were welded together and tightly packed into a 14.5-pound box.2 In this blog post, I look inside the premodulation processor, examine its construction, and describe how each module worked.

The premodulation processor with its case removed, showing some of the circuitry. (Click any image for a larger version.)

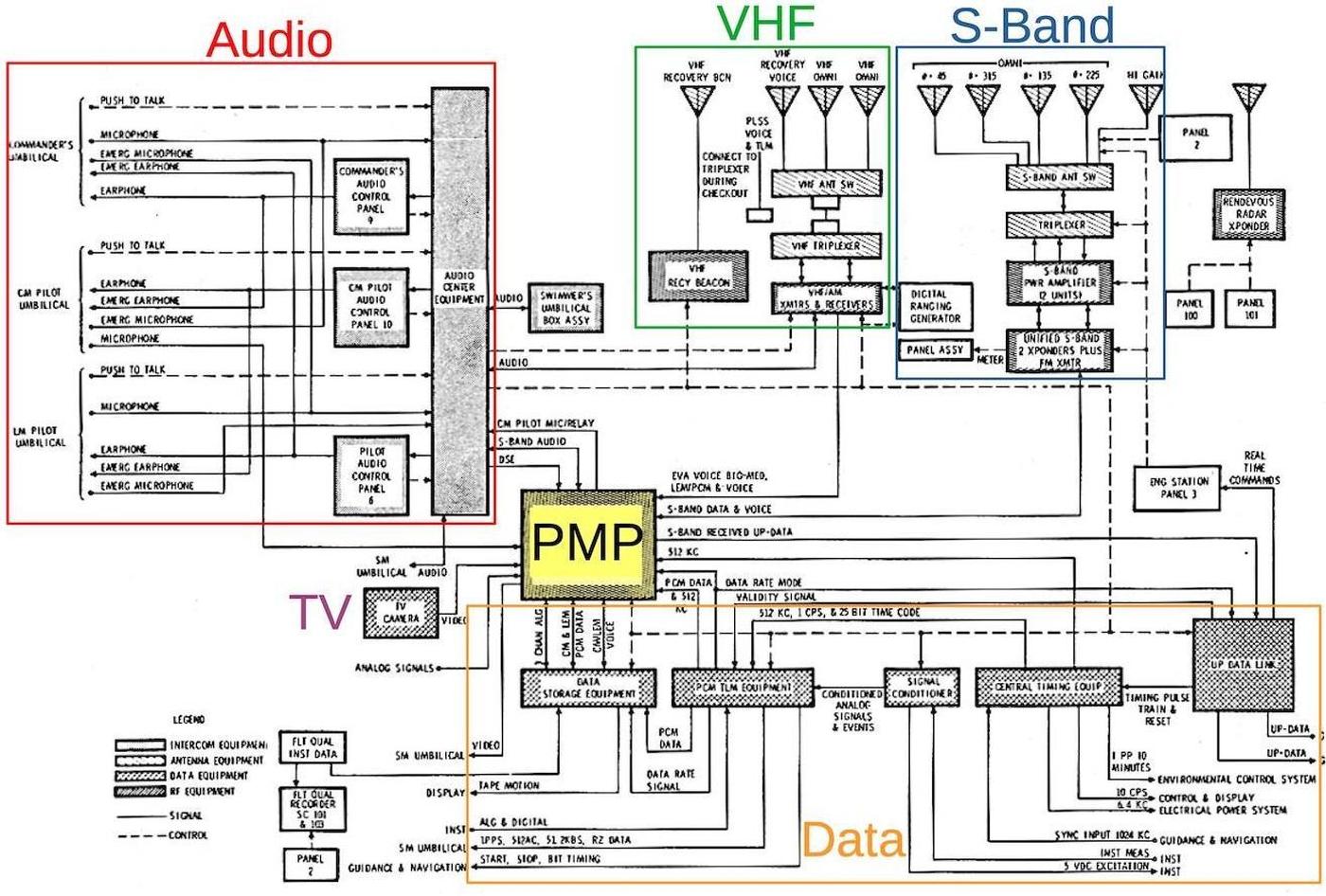
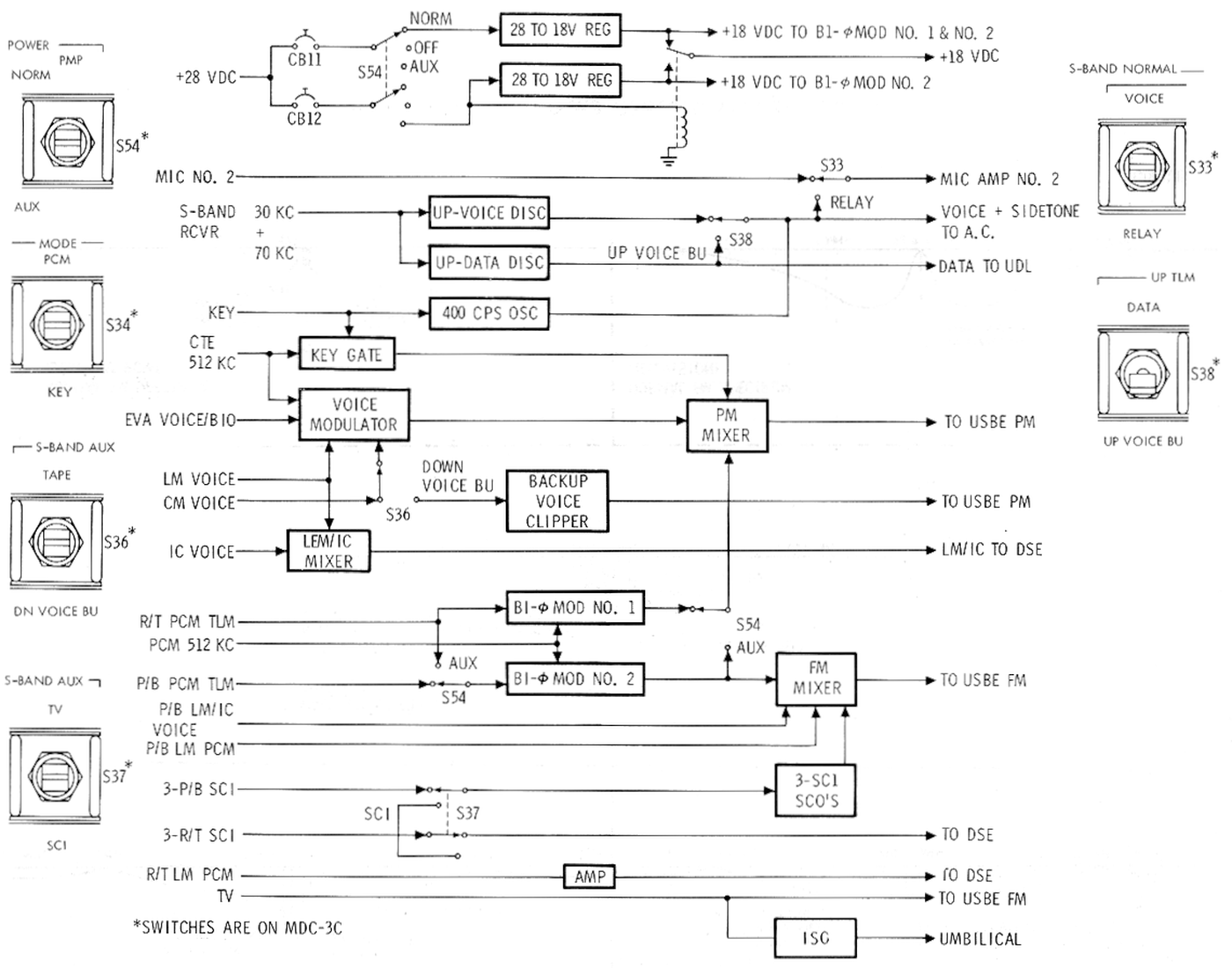
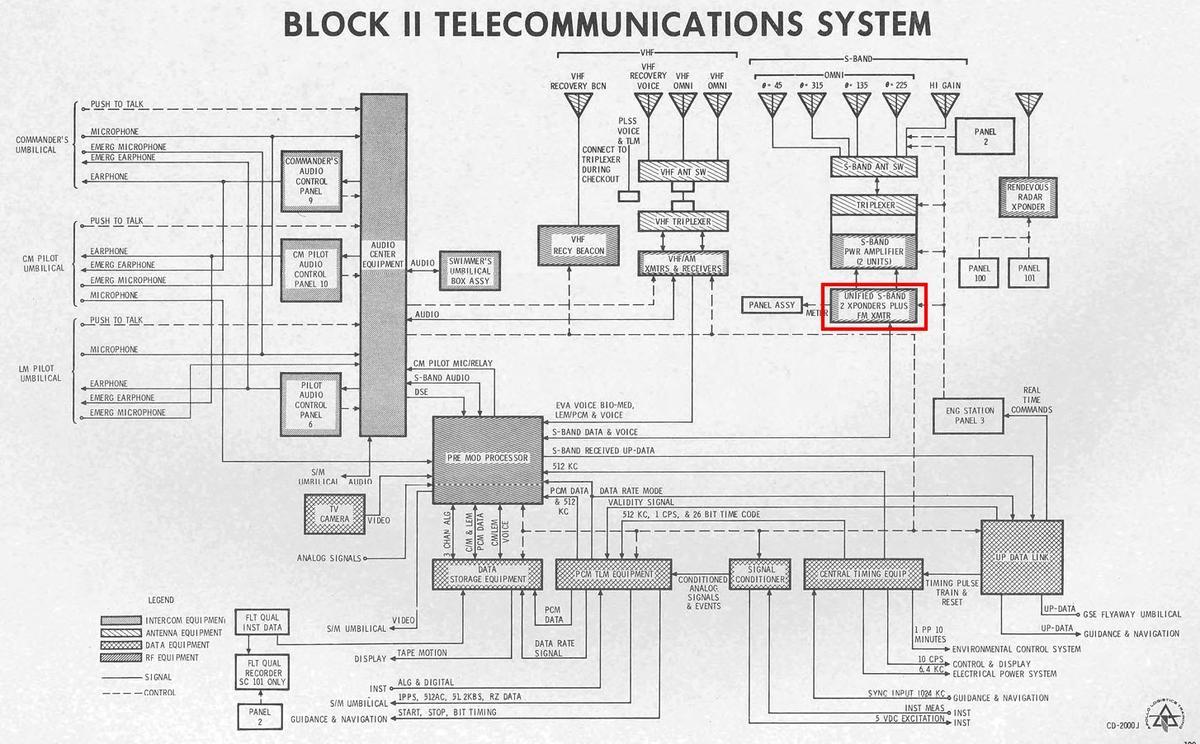
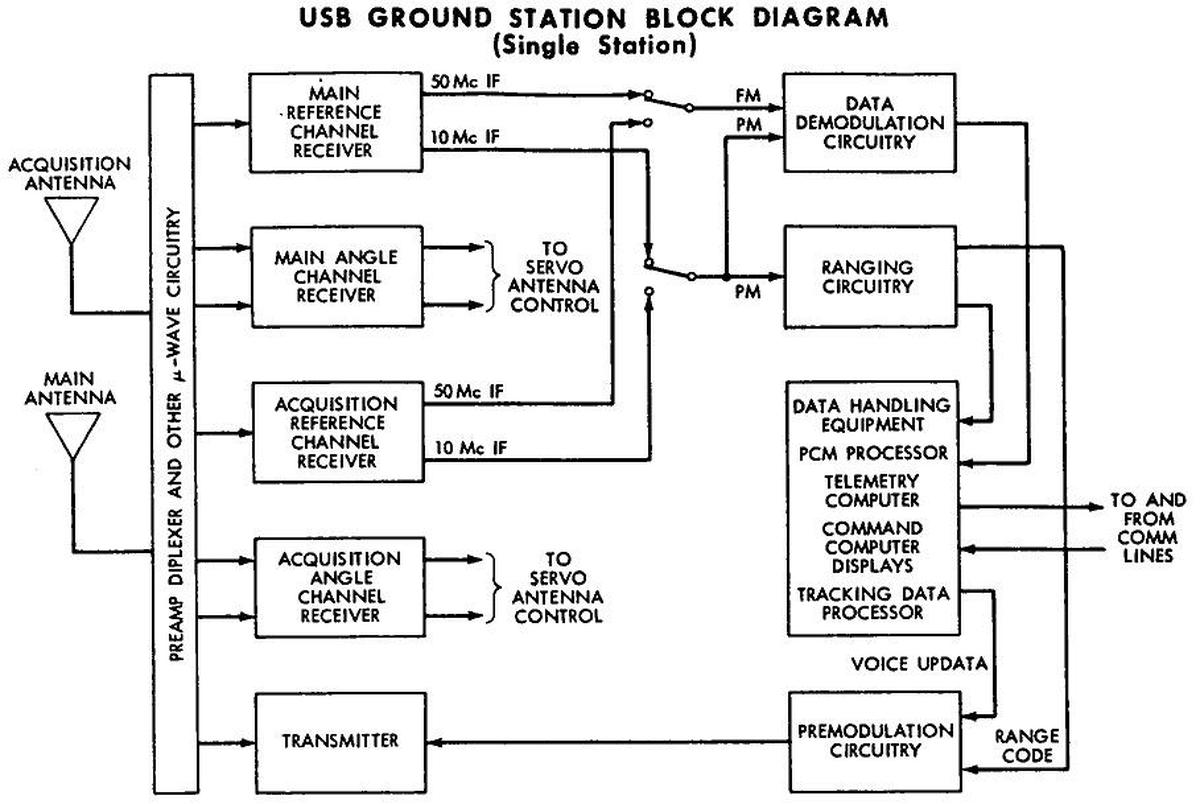
The communications systems in the Apollo Command Module were very complex, as shown in the block diagram below.3 The premodulation processor (PMP, yellow) played a central role: most of the audio (red), data (orange), and TV (purple) went through the premodulation processor, where the signals were combined for transmission by the S-band (blue) radio systems. The premodulation processor also handled most of the voice and data signals received from Earth or from the Lunar Module via the VHF (green) or S-band radio systems.

Block diagram of the Apollo communications system. From Apollo Operations Handbook: Telecommunications System page 3.

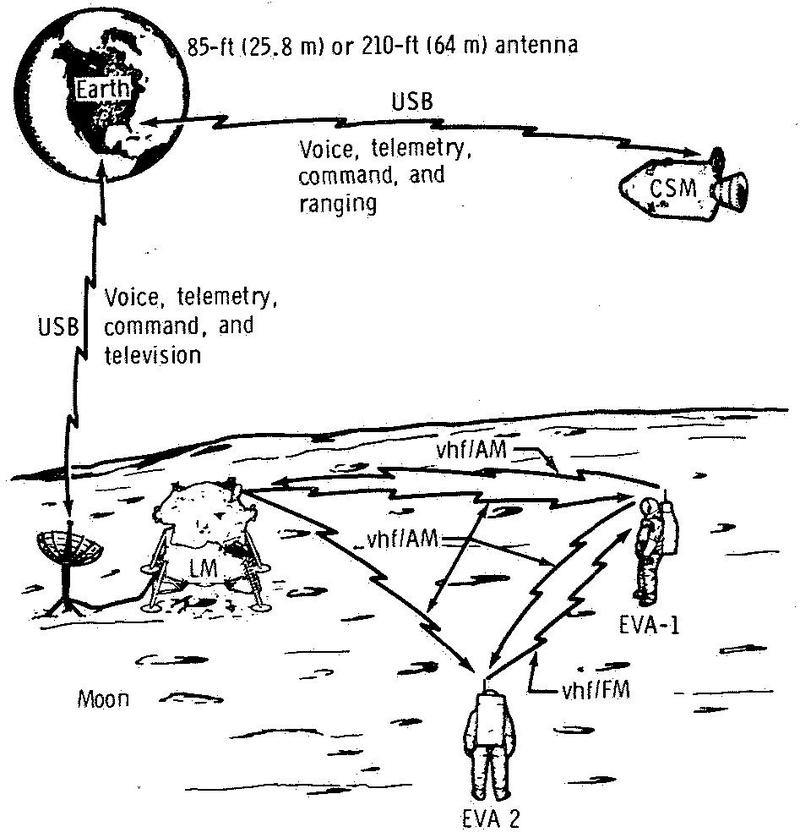
One reason for the complexity of the premodulation processor was that the audio system had to support a variety of communications configurations. The diagram below illustrates one configuration, when astronauts were walking on the Moon (i.e. extra-vehicular activity, EVA). They communicated with the Lunar Module on the Moon's surface via VHF/AM radio, which relayed their audio to Earth via the Unified S-Band (USB) radio. Meanwhile, the Command and Service Module (CSM) orbiting the Moon also communicated with Earth via S-Band. These voices were conferenced together so the astronauts and ground could all hear each other. The need for redundancy added to the complexity; for example, signals from the Moon could be relayed through the Command Module in the event of an equipment failure.

Typical Apollo communication for lunar surface operations. From Apollo Experience Report.

Construction

Like much of the Apollo electronics, the premodulation processor was packaged in a drab bluish metal case. The case has four round military-style connectors on top that linked the various audio, RF, and control signals to other components of the spacecraft.

This photo shows the premodulation processor inside its case.

We opened the case by removing the screws and inside we found 11 rectangular modules packed together tightly, from the power supply at the top to the "SCO & diff ampl" (subcarrier oscillator and differential amplifier) at the bottom, conveniently labeled with their functions. The modules were plugged into a thin backplane,5 at the right, connected by D-Sub connectors, similar to vintage RS-232 connectors but in a variety of sizes. Bundles of wires connected the backplane to the round connectors. This construction technique made it easy for us to remove the modules and inspect them individually.

A side view of the premodulation processor, showing the labeled modules.

The modules themselves don't use printed-circuit boards, but instead are built from components that are spot-welded to metal pegs, as shown below.6 These resistors, diodes, capacitors, and transistors are tightly packed with a jumble of overlapping wiring. Most of the wiring consists of the component leads, but point-to-point wiring provided additional connection. The wiring is a combination of color-coded insulated wires, bare wires, and bare wires in clear insulating tubes. The components are liberally covered in what looks like hot glue. I suspect that the hot glue was only used in equipment for ground testing, while modules for spaceflight were fully encapsulated to prevent short circuits.

A closeup of the wiring in the aux bi-phase modulator module. Most of the connections are spot-welded, although a few seem to have solder.

The modules have circuitry on both sides, which increased the density. About half of the metal pegs provide connection to the other side, while half have plastic stubs on one side. As will be seen below, many of the modules also contain rectangular metal sub-units that implement functional blocks such as oscillators or filters. It appears that these standardized functions could be bought "off-the-shelf", not as integrated circuits, but as blocks containing discrete components.

In the following sections, I'll discuss each module in more detail, starting with the power supply.

Power supply module

The premodulation processor contains a power supply that converted the spacecraft's 28-volt DC supply to 18 volts. For efficiency, it is a switching power supply, a buck converter that chops up the input power at a high frequency to drop it to the lower voltage. Although switching power supplies are now ubiquitous, in everything from phone chargers to PC power supplies, switching power supplies were expensive and rare in the 1960s, used in aerospace applications that required a compact, high-efficiency power supply.

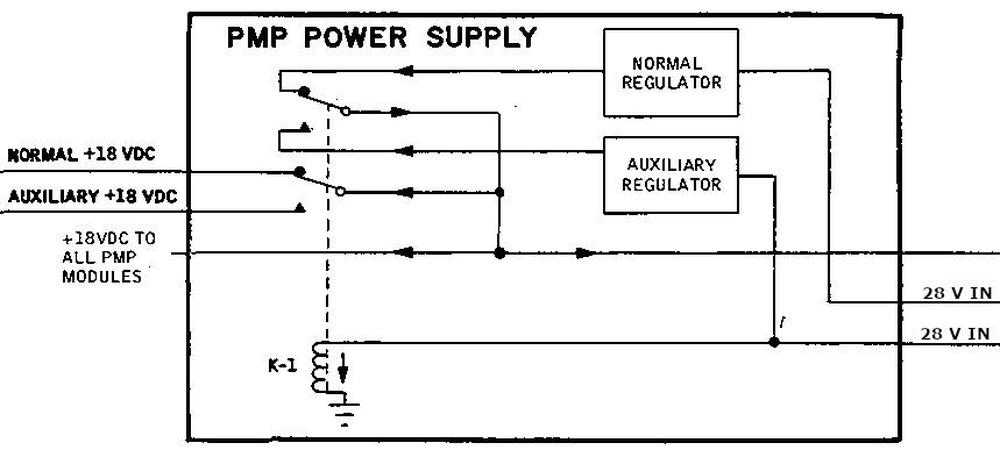
The block diagram below shows that the power supply was implemented redundantly, with a normal regular and an auxiliary regulator. A relay switches between the two regulators, controlled by the PMP NORM/AUX switch.

Diagram of the power supply module. From Command/Service Module Systems Handbook p63.

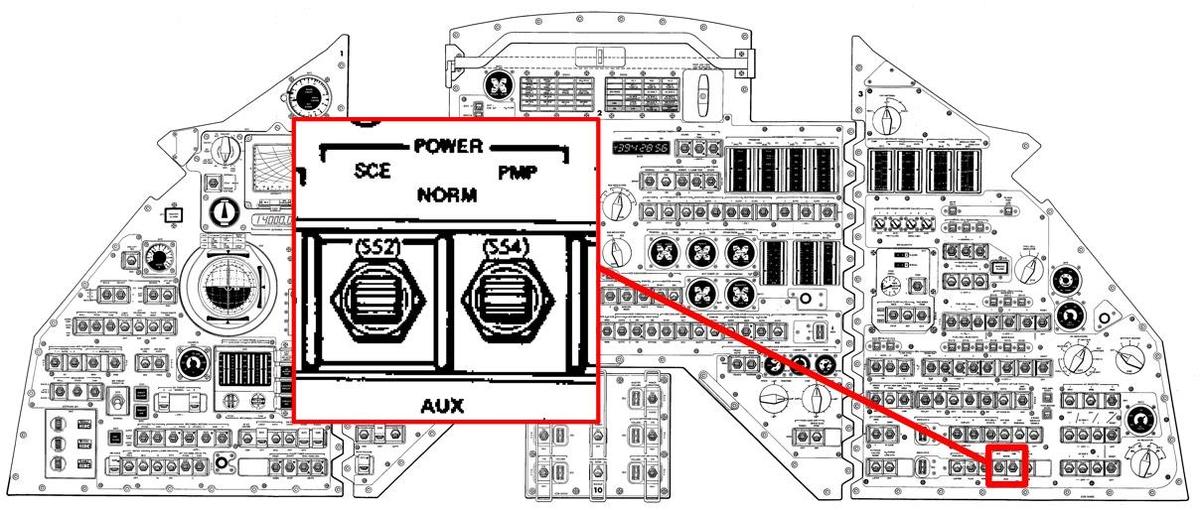
You may know of the Apollo 12 incident where the spacecraft was hit by lightning seconds after launch, scrambling the telemetry. The problem was resolved by the famous "set SCE to AUX" switch.7 The PMP's power switch is next to the SCE switch but never played a dramatic role.8

The power switches for the signal conditioning equipment (SCE) and the premodulation processor (PMP) are in the lower-left corner of the Command Module's control panel. Each switch has positions for NORM, OFF, and AUX.

The photo below shows the power supply module. The redundant halves of the power supply are visible with the lower circuitry a mirror image of the upper circuitry. The relay to switch between the two is the black box in the center-left. The power switching transistors are above and below the relay, fastened down with screws. To the right of the transistors are cylindrical tan inductors, storing energy across each pulse. Large silver filter capacitors are between the inductors. The right half of the module is the control circuitry: resistors, capacitors, transistors, and diodes. The connector at the far right connects the power supply to the other modules via the backplane.

The power supply module for the premodulation processor.

Flipping the power supply over reveals the high-frequency power transistors, in large metal packages to dissipate heat. These packages are square, unlike the typical two-tab (TO-3) power transistor packaging. Note the second layer of discrete component circuitry on this side of the module. This illustrates how the modules have two layers of circuitry, one on each side. You can also see the tops of the smaller transistors that are wired on the other side.

Underside of the power supply with 2N3137 power transistors.

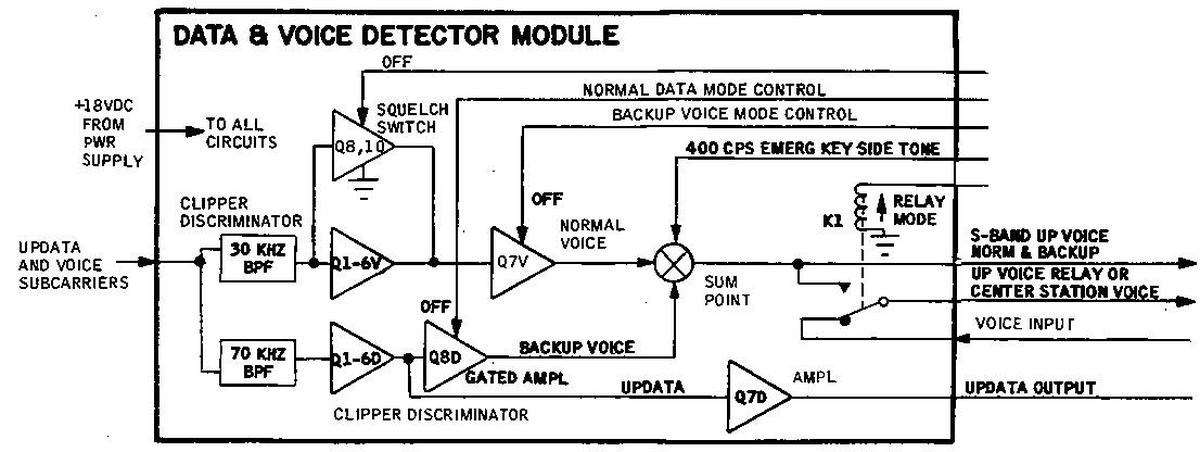
Voice and data detector module

The data and voice detectors handle signals transmitted to the spacecraft over the S-band. The S-band transceiver receives these signals, demodulates them, and passes the signal to the premodulation processor. The data and voice detectors appear as one module on the block diagram below but are implemented as two modules physically.

Diagram of the data and voice detector modules. From Command/Service Module Systems Handbook p63.

The photo below shows the voice detector module. Voice is transmitted to the spacecraft, frequency modulated onto a 30-kilohertz subcarrier. The voice detector extracts this signal through a 30-kilohertz bandpass filter, demodulates it with an FM discriminator, amplifies it, and sends it to the Audio Center, which provides it to the astronauts. The largest component of the module is the 30-kilohertz bandpass filter at the center top. This module was built by Bulova Electronics, a division of the watch company that produced quartz crystals, oscillators, filters, servo amplifiers, and other components. Two gray transformers are also visible; these coupled the audio signals. The black relay in the lower right was controlled by the "Up Voice Relay" console switch. (Don't be confused by the two completely different definitions of "relay".)

The circuitry of the voice detector module. The connector is on the left.

More circuitry is on the other side of the voice detector. The transformers, relay, and bandpass filter are visible through openings in the module's metal frame. The discrete components are arranged in orderly columns, unlike the other modules.

The other side of the voice detector module.

The data detector module operated similarly to the voice detector, except that it extracted the data link signals from ground. From the data detector module, data was processed by the Up-Data Link box, giving the ground control over multiple spacecraft systems. For instance, commands could be entered into the Apollo Guidance Computer. The spacecraft clock (CTE, Central Timing Equipment) could be set. Various relays could be controlled, overriding some of the switches on the console.

The data detector module. It contains a 70-kilohertz bandpass filter produced by Bulova.

The implementation of the data detector module (above) is similar to the voice detector module, but simpler since it doesn't have the summing and switching circuitry. It uses a 70-kilohertz bandpass filter module, rather than the voice detector's 30-kilohertz filter. In case of a malfunction with the voice detector, backup voice communication could be transmitted to the spacecraft over the 70-kilohertz subcarrier, and extracted by the data detector module. This mode was controlled by the "Up-voice backup" switch.

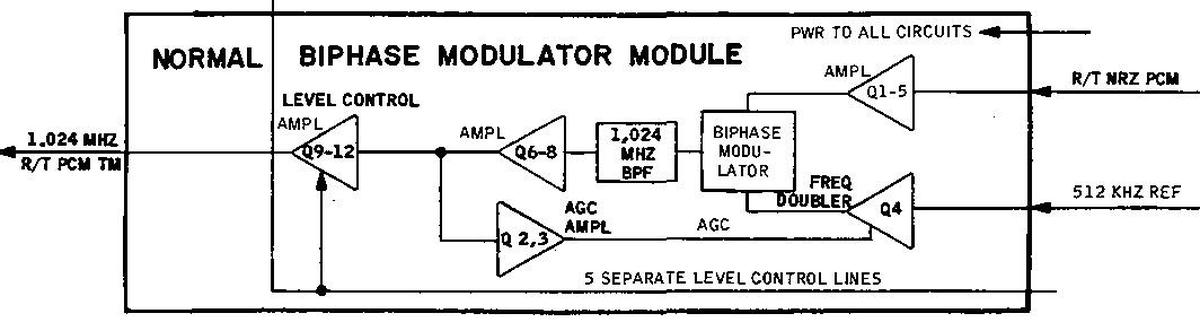
Bi-phase modulator modules

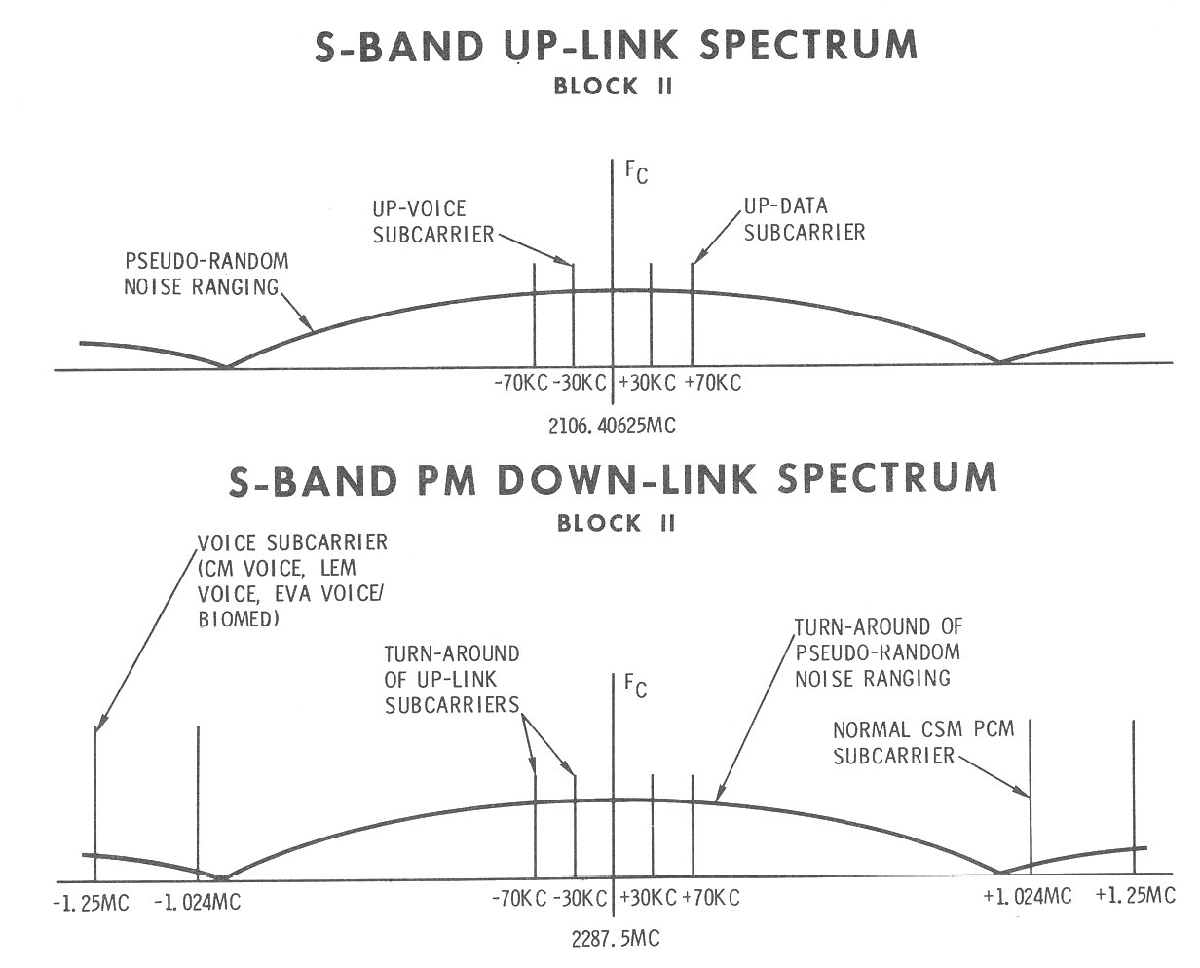
The role of the bi-phase modulator modules was to modulate telemetry data using bi-phase modulation. In total, data had three layers of modulation. First, data was digitally encoded using pulse-code modulation (PCM). Next, this module applied bi-phase modulation to the bits at 1.024 MHz. Finally, the S-band transceiver used FM or PM (frequency or phase modulation) for the communication to Earth.

Bi-phase modulation encodes a bit using a sine wave for a 1 and an inverted sine wave for a 0 (i.e. a phase shift of 180°). Bi-phase modulation is a type of phase-shift keying. The PCM data was at 51.2 kilobits per second ("high bit rate") or 1.6 kilobits per second ("low bit rate"). Since the data was modulated at 1.024 MHz, a bit was encoded by at least 20 cycles of the waveform. This gave the receiver plenty of time to determine the phase and distinguish a 0 from a 1.

Diagram of the normal bi-phase module. From Command/Service Module Systems Handbook p63.

The premoduation processor contains two modulator modules: the "normal" module and the "auxiliary" module. The normal module transmits real-time data over PM, while the auxiliary module is more flexible. The normal bi-phase modulator module (below) contains a complex tangle of circuitry. The 1.024 MHz bandpass filter is the large metal package at the right, limiting the output signal to a narrow frequency range around 1.024 Mhz.

Inside the bi-phase modulator module.

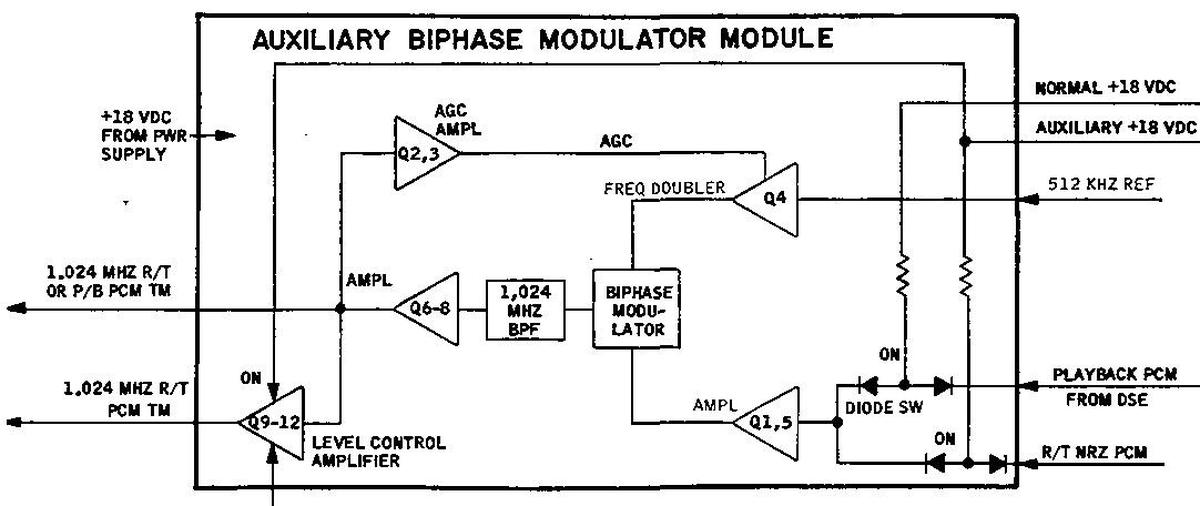
The auxiliary bi-phase modulator (below) is roughly the same as the normal modulator, but with a bit more circuitry to switch between modes, transmitting either recorded PCM data from tape or real-time PCM data, using the PM or FM transmitters. Curiously, the different modes are selected by switching the power supply between NORM and AUX. In NORM mode, the auxiliary module transmits recorded data over FM. In AUX mode, the auxiliary module transmits real-time data over both PM and FM, providing a backup in case the normal module fails.

Diagram of the auxiliary bi-phase module. From Command/Service Module Systems Handbook p63.

The output signals from the bi-phase modulators are processed either by the FM mixer / LM PCM limiter module or the PM mixer / key / TV module; these are discussed later.

Underside of the auxiliary bi-phase modulator. The bandpass filter is at the left.

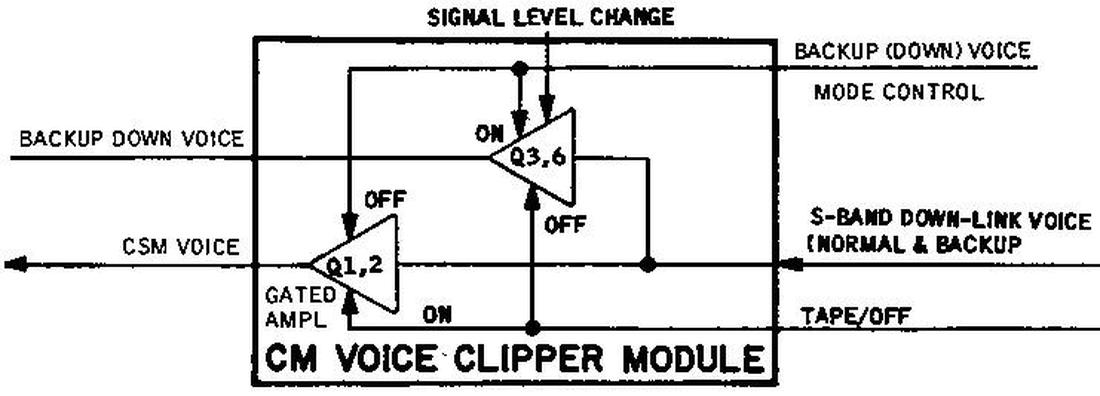
Voice clipper module

Voice communication from astronauts to the ground ("downlink voice") went through multiple stages of processing to improve quality. The design standard for the Apollo audio system was 90% word intelligibility for the main links and 70% for the backup links.9 This standard seems surprisingly poor, with one out of 10 words unintelligible, but achieving this standard was challenging due to the extreme distance to the Moon. Moreover, the spacecraft had a lot of ambient noise that interfered with communication. To maximize voice intelligibility over the available radio link, the voice signal was pre-emphasized and clipped. The voice clipper module (below) implemented the pre-emphasis and clipping of the voice signal.

Diagram of the voice clipper module. From Command/Service Module Systems Handbook p63.

The photo below shows the voice clipper module. It has two gray audio transformers at the left. The remainder of the module is filled with circuitry.

The voice clipper module.

The voice signal next goes to the voice relay module, discussed below. (The backup voice signal, however, went directly to the S-band transceiver for transmission to ground.)10

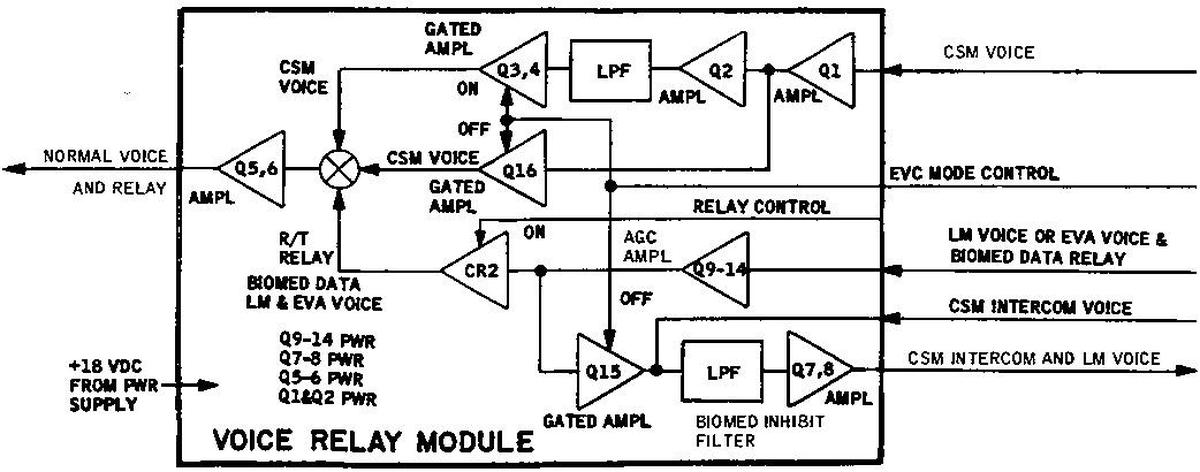
Voice relay module

The voice relay module permitted voice communication from the Lunar Module to be relayed through the Command Module instead of being transmitted directly to Earth from the Lunar Module. If the S-band mode switch was set to "RELAY", the voice and biomedical data from the Lunar Module would be mixed in with the Command Module's voice signal and sent to Earth. This module also optionally applied a low-pass filter to the Command Module's voice signal, under the control of the VHF duplex switch. (I think this is so voice and biomed data can be sent over the same channel without frequency conflict.)

Diagram of the voice relay module. From Command/Service Module Systems Handbook p63.

The photo below shows the voice relay module circuitry. There are three audio transformers, along with circuitry liberally encased in goo.

The voice relay module.

Flipping the module over, the upper right corner is completely covered in plastic. The reason for this is unclear. That corner holds one of the transformers, but I don't see a reason why this one in particular would be covered.

The other side of the voice relay module.

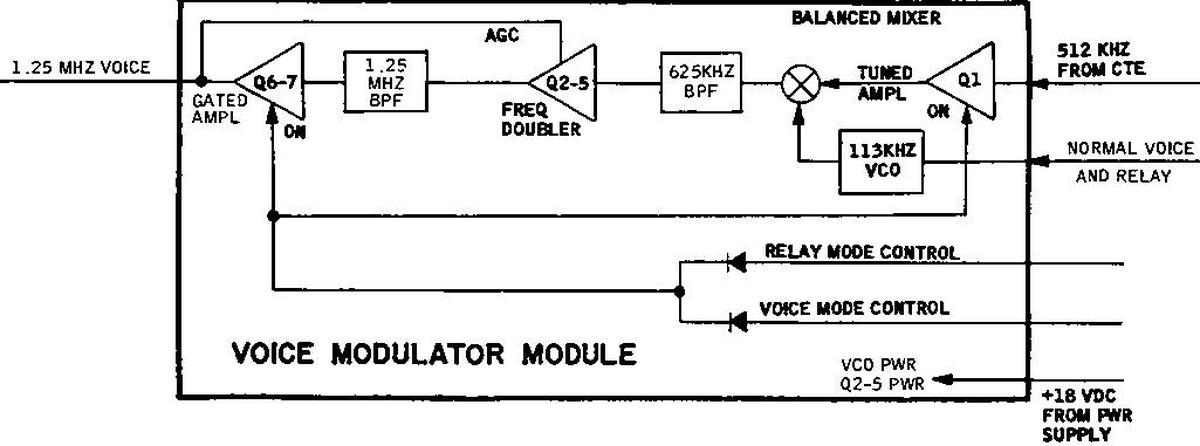
Voice modulator module

Next, the voice signal went to the voice modulator module, which used a complicated circuit to apply frequency modulation. First, the voice signal controls a 113-kilohertz voltage-controlled oscillator (VCO), yielding an FM signal at 113 kilohertz. Next, this signal is mixed with a 512-kilohertz signal from the central timing equipment (CTE), yielding signals at the sum and difference frequencies (399 kHz and 625 kHz). The bandpass filter passes the 625-kilohertz FM signal. The signal frequency is doubled and filtered to produce the final 1.25 MHz FM signal.

Diagram of the voice modulator module. From Command/Service Module Systems Handbook p63.

Three large modules are visible inside: the voltage-controlled oscillator and the two bandpass filters.

Inside the voice modulator module.

The other side of the module has the circuitry, wired to the larger modules. The frequency-doubler may be implemented by a varactor diode, but I haven't located it. From the voice modulator, the voice signal passed to the PM mixer / key / TV module.

Another view of the voice modulator module.

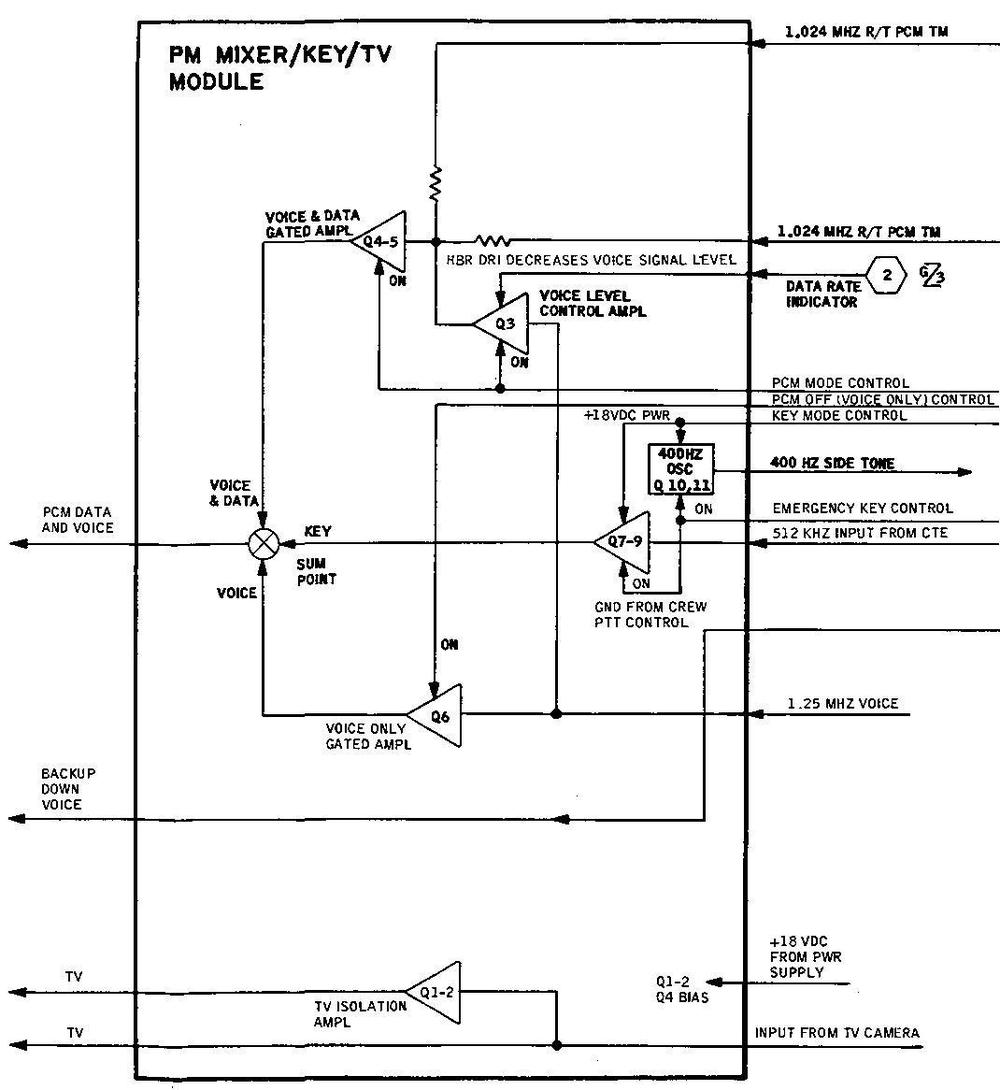
PM mixer/key/TV module

As the name suggests, the PM mixer/key/TV module had multiple functions. In the top part of the diagram below, the mixer combines three data sources: voice with data, emergency keying, and voice. The voice and data combination consists of PCM data at 1.024 megahertz with voice data at 1.25 megahertz; the PCM data is provided by one of the bi-phase modulator modules, while the voice data is provided by the voice modulator module. The next mixer input is the emergency key signal. The purpose of emergency key is that if voice communication failed, an astronaut could send Morse code by using the XMIT key on their communication cable. This key signal might be able to get through to Earth even if voice communication fails or is unintelligible. This module produces the emergency key signal at 512 kHz along with a 400 Hz feedback tone for the astronauts. The final mixer source is voice. The sum of these signals is sent to the S-band PM transponder for phase modulation and transmission. This module also includes a TV isolation amplifier to supply a TV signal to ground support equipment (GSE) before launch.

Diagram of the PM mixer / key / TV module. From Command/Service Module Systems Handbook p63.

The photo below shows this module. On the front right is a component that looks a bit like a power transistor. However, it is an adjustable component (note the screw in the middle), probably a variable resistor.

The PM mixer / key / TV module.

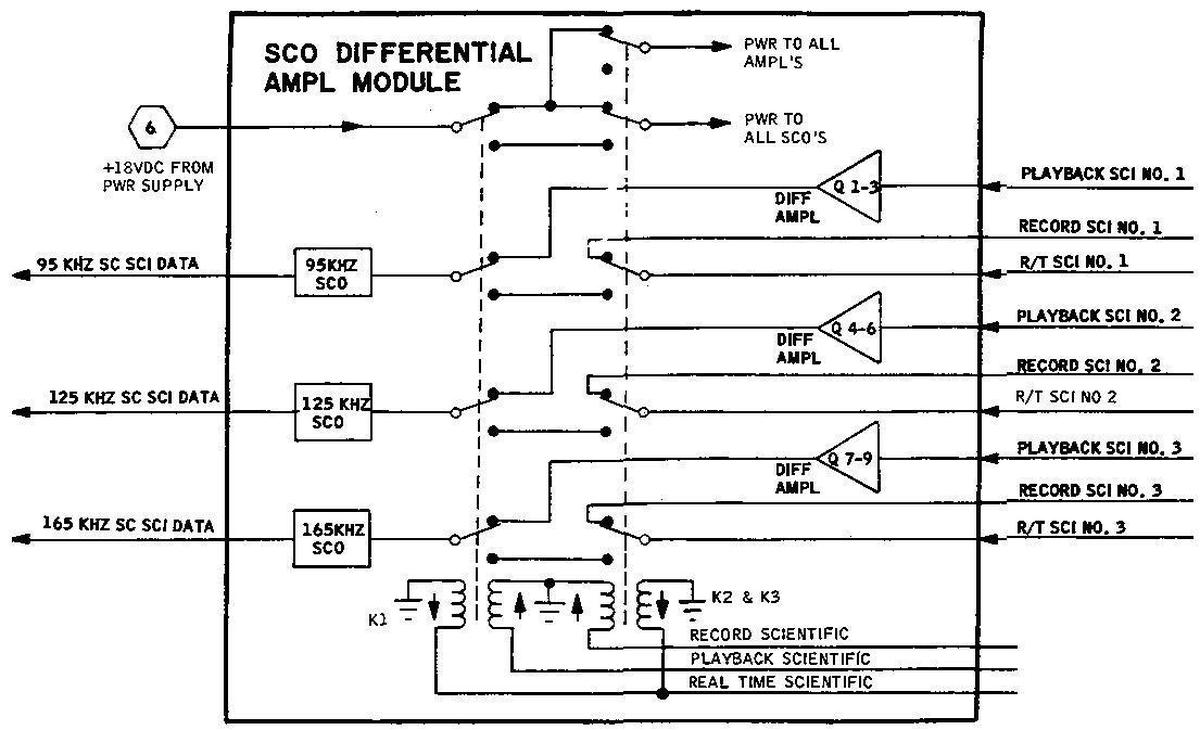
SCO (subcarrier oscillator) and differential amplifier

This module is used for transmitting three channels of analog scientific data. (This is in contrast to most of the data, which was transmitted digitally, using pulse-code modulation (PCM).) Each of the three scientific signals modulates a subcarrier oscillator on a different frequency: 95 kHz, 125 kHz, and 165 kHz. These signals are sent to the FM mixer / LM PCM limiter module, which will be discussed in the next section.

This module also contains relays so the real-time scientific data could be directed to tape for storage. The recorded data could be played back for transmission, amplified by the differential amplifiers. The mode was controlled by the S-band Aux TV/SCI switch. If set to SCI, real-time scientific data was transmitted. If the transmitter was used for TV, the scientific data was recorded to tape for later playback. The tape recorder switch was set to PCM/ANLG to play back the analog data.

Diagram of the SCO differential amplifier module. From Command/Service Module Systems Handbook p63.

Inside, the three large tan oscillator modules are visible. The three relays are the smaller grayish boxes. This module has the D-Sub connector attached with wires and rotated 90°, unlike the other modules that have the connector mounted to the end of the module.

The SCO & differential amplifier module.

On the other side of the module, the circuitry is visible. Note the 6-pin transistors (gold and green circles). These probably contain two carefully-matched transistors for the differential amplifiers. The performance of a differential amplifier strongly depends on its two input transistors; by putting the transistors in the same package, the effects of temperature are minimized.

Another view of the SCO & differential amplifier module.

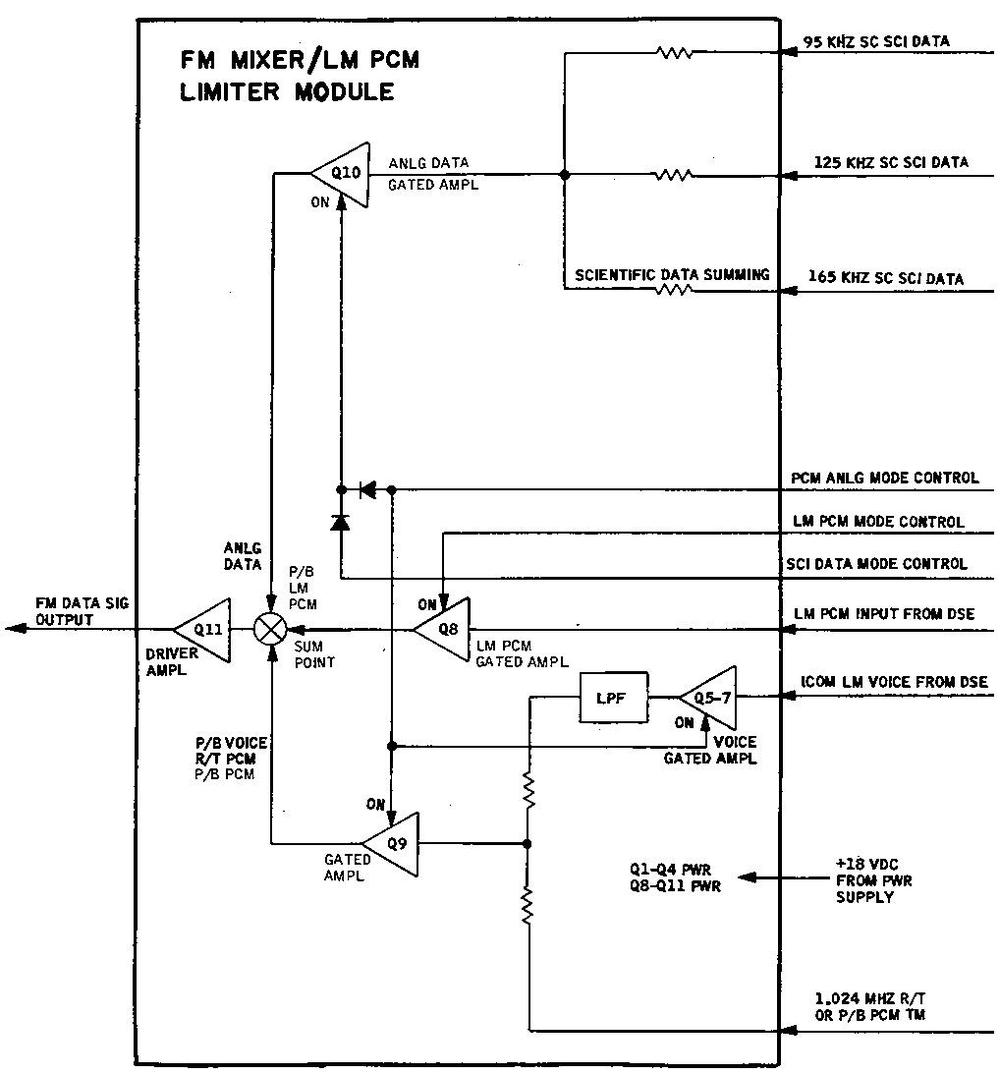
FM mixer / LM PCM limiter module

The final module is the FM mixer / LM PCM limiter. Like the PM mixer module, this module combines multiple signals for transmission. But this module prepares signals for FM transmission rather than PM transmission. Specifically, the module combines the three analog scientific data inputs, digital PCM data from the Lunar Module, intercom voice from the Lunar module, and PCM data modulated at 1.024 MHz. Various switches on the console control the different modes.

Diagram of the FM mixer / LM PCM limiter module. From Command/Service Module Systems Handbook p63.

The photo below shows the module's circuitry. It has four gray transformers along with the typical transistors, diodes, resistors, and capacitors.

The FM mixer / LM PCM limiter module.

The unusual feature of this module is the encapsulated module in the upper left. This module appears to contain three transistors and five capacitors. It's unclear why these components are encased in plastic. The block diagram for this module doesn't show any special circuitry that would motivate encapsulation. I hope to reverse-engineer this module to figure this out.

The encapsulated block appears to contain three transistors and five capacitors.

Conclusion

Well, I had planned to write a quick description of what we saw inside the premodulation processor but it turned out to be much more complicated than I expected. Congratulations on making it to the end of this blog post.

The premodulation processor illustrates how analog electronics were very bulky before integrated circuits became popular. In the modules, amplifiers and other functional blocks were built from discrete components. The result was a 14.5-pound box to perform a few signal processing tasks. A decade later, many of the circuits could have been replaced with compact ICs.

The premodulation processor also shows how complex everything was in Apollo. You might think that transmitting voice, data, and TV wouldn't be too tricky, just three signals. But everything needed to be redundant. Then there were special cases, such as recording data when you're on the far side of the Moon. Or communicating between astronauts in the Command Module, in the Lunar Module, and walking on the Moon. All these cases required circuitry to switch signals and optimize the radio link for each mode. And the premodulation processor is just one of many boxes in the Apollo communications system! Apollo is like a fractal, where you find successive layers of complexity as you look closer at any system.

We haven't been able to find detailed schematics of the premodulation processor modules, so I plan to reverse-engineer some of the circuitry. I announce my latest blog posts on Twitter, so follow me @kenshirriff for updates. I also have an RSS feed. Thanks to Marcel for providing the premodulation processor and letting Mike, CuriousMarc and me disassemble it.

Front view of the premodulation processor with the case removed.

Notes and references

1. The Apollo Operations Handbook: Telecommunications System gives this description: "The premodulation processor (PMP) equipment provides the interface connection between the airborne data-gathering equipment and the RF electronics. The PMP accomplishes signal modulation and demodulation, signal mixing, and the proper switching of signals so that the correct intelligence corresponding to a given mode of operation is transmitted." ↩

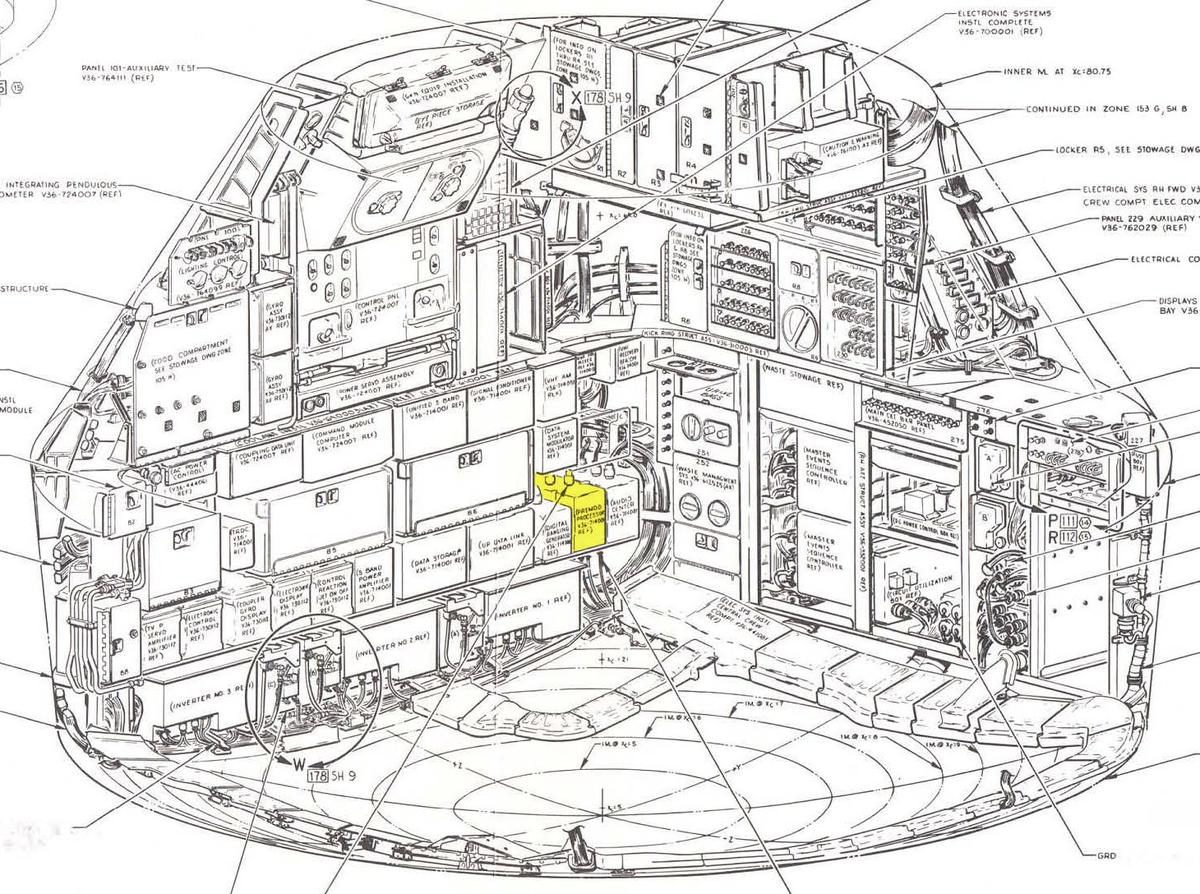
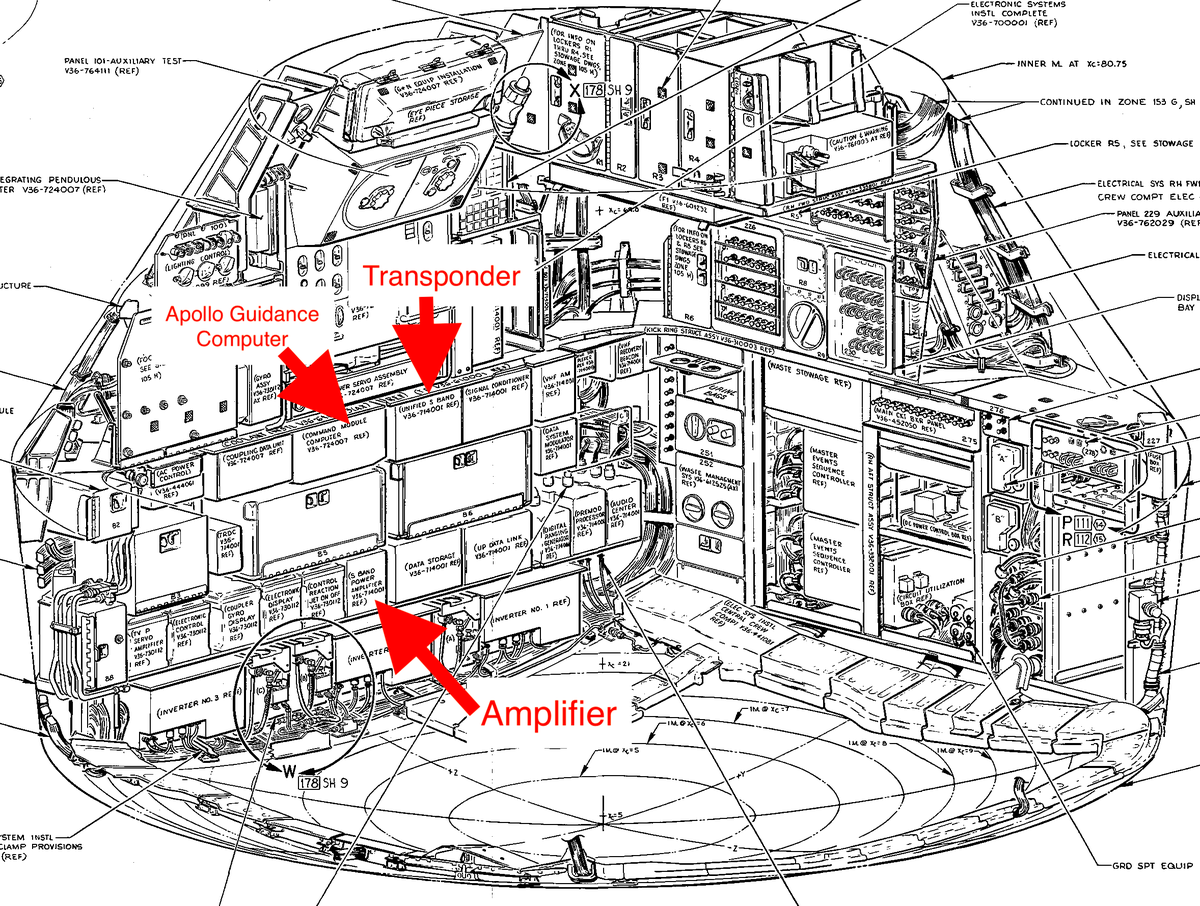
2. The premodulation processor was one of many boxes of electronic circuitry packed into the spacecraft and linked by thick cables. The diagram below highlights where it was mounted in the lower equipment bay of the Apollo Command Module.

   

   The premodulation processor was one of many electronic boxes in the Command Module's lower equipment bay. Diagram from Command/Service Module Systems Handbook p212.

    ↩

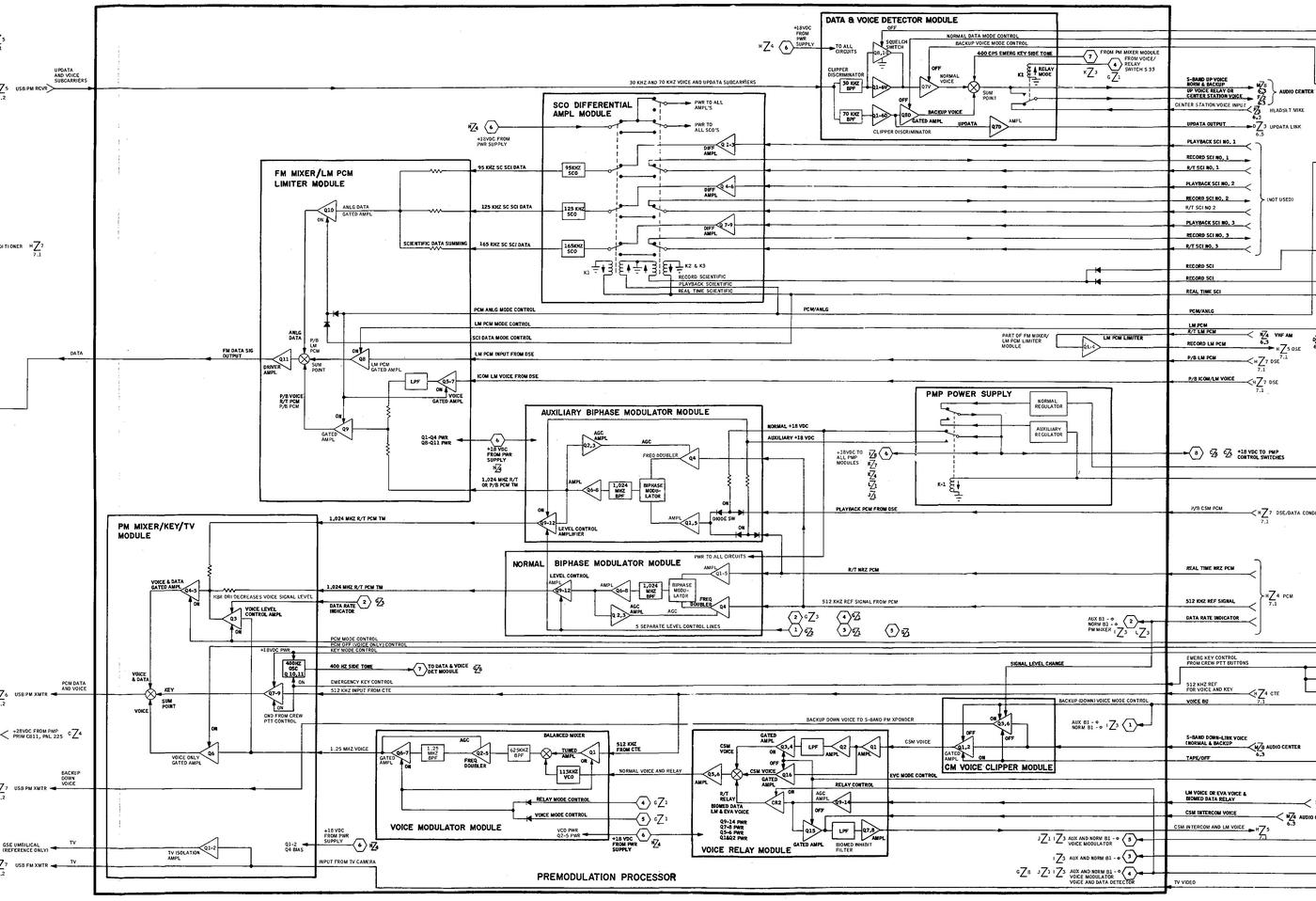
3. The block diagram below shows the functions of the premodulation processor, along with the switches that control it.

   

   A block diagram of the premodulation processor. From Apollo Operations Handbook: Telecommunications System.

   The block diagram below provides a more detailed view of the premodulation processor. I split out the sub-module diagrams for the discussion, but the full diagram shows the interconnections between the modules.

   

   Block diagram of the PMP. (Click for a larger version.) From Command/Service Module Systems Handbook p63.

    ↩

4. As shown by the nameplate, the premodulation processor was built by Collins Radio in 1966, two days before Christmas. Collins Radio built much of the communications equipment for the space program from Mercury through Apollo including the Deep Space Network antenna system, microwave links, and ground support equipment (details).4

   

   The nameplate for the premodulation processor shows that it was built by Collins Radio.

    ↩

5. The backplane is a sheet of metal with D-Sub connectors for each module. The round connectors are underneath, wired to the backplane by individual wires.

   

   The premodulation processor's backplane links the modules to the external connectors.

   The four round military-style connectors are shown below. Two connectors have individual pins, while two connectors each have tiny coaxial connections.

   

   The premodulation processor had four connectors for its numerous audio, RF, and control signals.

    ↩

6. We've examined several different Apollo electronics boxes and surprisingly they use completely different manufacturing techniques, even for boxes built by the same manufacturer. Techniques we've seen include printed-circuit boards, surface-mount components, cordwood modules, "dead-bug" components on a ground plane, point-to-point components, and encapsulated hybrid modules. I expected that there would be a standard manufacturing technique (like PCBs are standard now), but everything is different. ↩

7. The story of "Set SCE to Aux" is a well-known Apollo incident where disaster was averted. In brief, Apollo 12 was struck twice by lightning just seconds after launch. Inside the spacecraft, so many warning lights lit up that astronaut Conrad thought "the whole board looks like a Christmas tree". On the ground, consoles started displaying nonsense telemetry. Everyone was mystified until engineer John Aaron recalled seeing similar garbled telemetry during a test. He knew the solution and gave the puzzling command "Try SCE to Auxiliary". This switch was so obscure that astronaut Conrad responded, "What the hell is that?" Fortunately, astronaut Bean flipped the switch, bringing the SCE unit back to operation and restoring telemetry. There were other consequences of the lightning strike, but after the fuel cells were brought back online and the inertial guidance system was realigned, the spacecraft continued uneventfully to the Moon.

   The underlying problem was that the lightning strike caused the spacecraft's fuel cells to go offline. The DC voltage bus was supposed to be at 28 volts, but the loss of the fuel cells caused the voltage to sag to about 18 volts. Within milliseconds, the voltage climbed to 24 volts under battery power, still low. The low voltage caused the primary power supply of the SCE (signal conditioning equipment) to shut down. Since the SCE's role was preparing dozens of analog sensor voltages for telemetry, this caused the telemetry values to Mission Control to be garbled. Flipping the SCE switch to Aux caused the SCE to use its auxiliary power supply, restoring the SCE to operation.

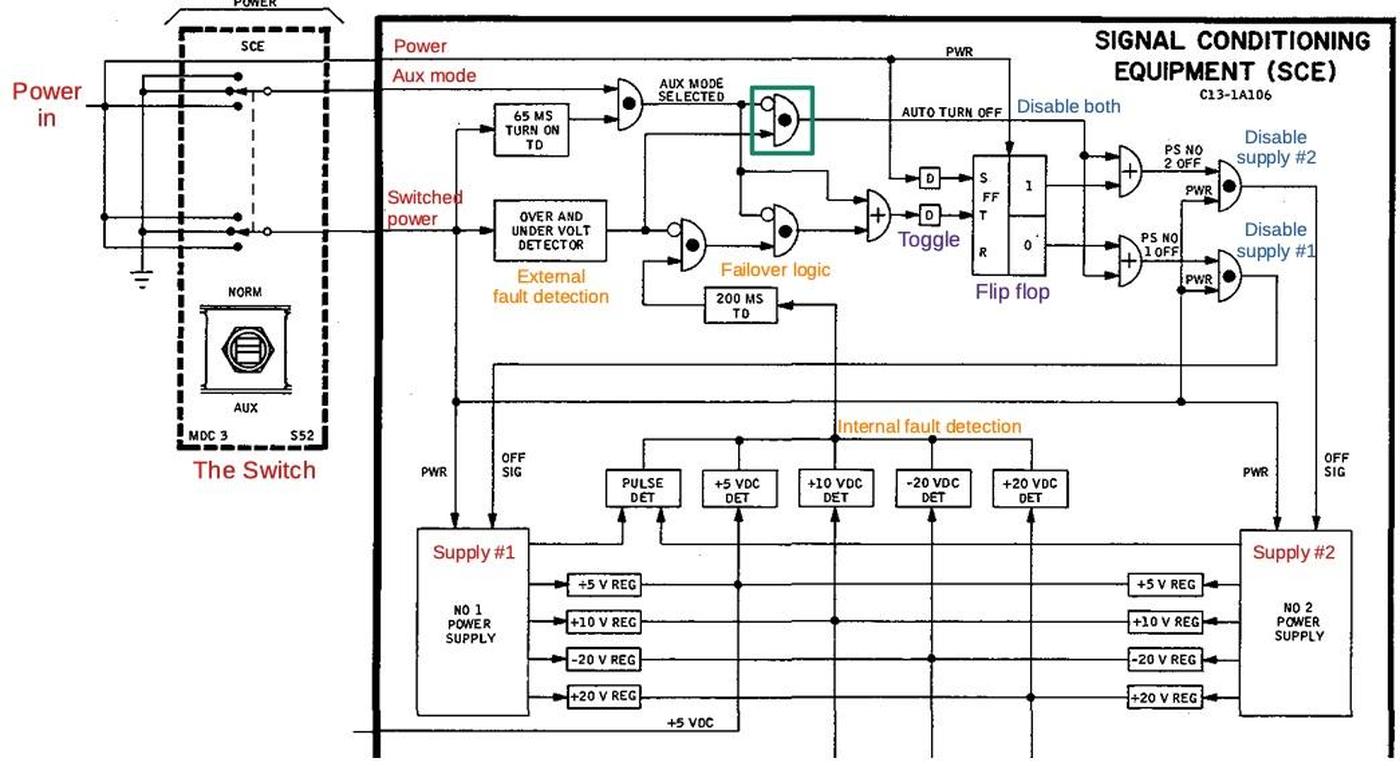
   The published descriptions of this incident are vague on exactly why the auxiliary power supply worked when the primary didn't, so I looked at the SCE diagram (below) to fill in a few details. Power enters at the left and passes through the SCE's famous power switch, which has three positions: NORM, OFF, and AUX. Inside the SCE, there are two power supplies (red) for redundancy, along with some control circuitry at the top. One of the two power supplies is active at a time, unless both power supplies are deactivated for an overvoltage or undervoltage condition.

   

   Diagram of the SCE power supply and the switch. From Command/Service Module Systems Handbook p118.

   The SCE has a flip flop (purple) that selects a power supply by disabling (blue) the unused one. When you switch SCE to AUX, one action is that it toggles the flip flop, switching from supply #1 to #2, or #2 to #1. But I don't think that was important for Apollo 12. AUX mode also blocks the undervoltage signal via an AND gate (green). That is, if the input voltage was still too low, both power supplies would be shut down in NORM mode but either one could function in AUX mode. This, I think, is why "SCE to AUX" powered up the SCE.

   Another interesting feature is the automatic failover (orange). In NORM mode, the SCE will automatically switch power supplies if an internal voltage is bad for 200 ms. However, the failover logic is blocked by the undervoltage detector, so it would not have taken place in Apollo 12. But otherwise, if one of the power supplies failed, the SCE would transparently switch to the other one.

   Curiously, the official NASA report Analysis of Apollo 12 Lightning Incident barely has two sentences on the SCE in its 94 pages. Although the SCE gets all the public attention in this incident, it seems like NASA didn't really care about it since the telemetry wasn't critical to the mission. NASA was much more interested in other effects of the lightning strike: the fuel cell shutdown, the effects on the computer and guidance systems, 9 failed sensors, and potential effects on the pyrotechnics. For more on the Apollo 12 incident, see the transcript, the detailed Scott Manley video, and an Apollo Flight Journal post.

   Note that the SCE's power supply logic is different from other units. Most units (such as the transponder, TWT amplifier, and premodulation processor) have primary and secondary power supplies, with a switch to explicitly select one or the other. However, in the SCE, the Aux switch toggles between power supplies, rather than selecting a specific auxiliary power supply. ↩

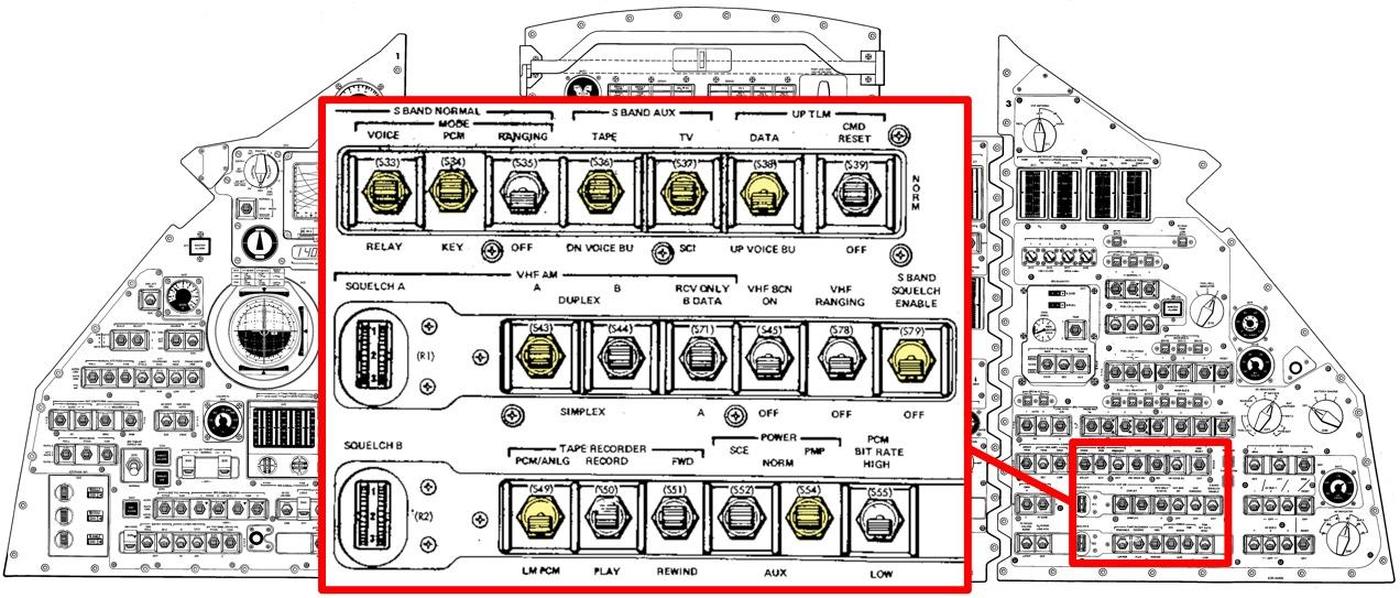
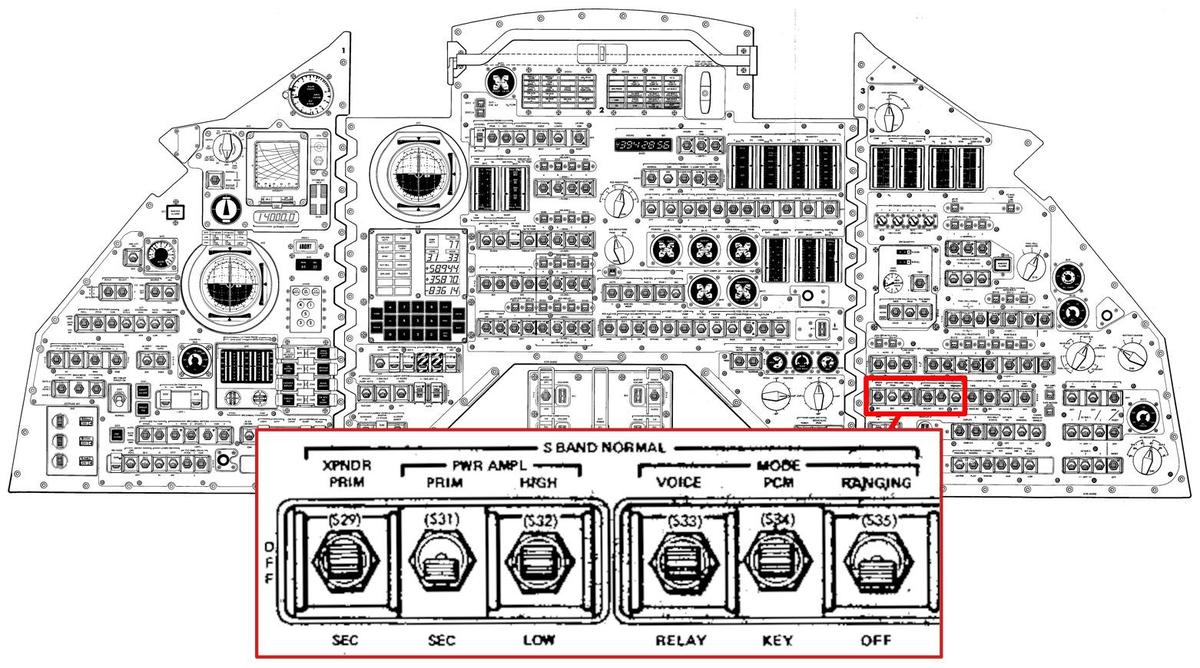
8. Astronauts used multiple switches on the control console to control the premodulation processor. These switches were grouped in the lower-right corner of the console with other communications switches. The diagram below shows the relevant switches, highlighted in yellow.

   ↩

   The Command Module console contains switches to control the premodulation processor. These switches are highlighted in yellow. Diagram based on from Command/Service Module Systems Handbook p208.

9. For detailed information on the voice communication system, see Apollo Experience Report - Voice Communications Techniques and Performances. It discusses the performance requirements for the Apollo communications system and how the system was designed to achieve the intelligibility requirements. ↩

10. The idea of backup voice was to provide a voice channel for emergencies that used less power, at the cost of garbling up to 30% of the words. After the explosion, Apollo 13 used the backup voice system so they could turn off the Lunar Module's power amplifier and conserve electrical power. (See Apollo 13 Mission Operations Report pages N-2 and N-7, as well as the transcript.) Backup voice was also used at times during Apollo 16 due to a failure of the Lunar Module's steerable S-band antenna; see Apollo 16 Mission Report page 7-3, which calls this mode "down voice backup". (I should point out that these backup voice incidents involved the Lunar Module, not the Command Module's premodulation processor.) ↩

The digital ranging system that measured the distance to the Apollo spacecraft

During the Apollo missions to the Moon, a critical task for NASA was determining the spacecraft's position. To accomplish this, they developed a digital ranging system that could determine the distance to the spacecraft, hundreds of thousands of kilometers away, with an accuracy of about 1 meter.

The basic idea was to send a radio signal to the spacecraft and determine how long it takes to return. Since the signal traveled at the speed of light, the time delay gives the distance. The main problem is that due to the extreme distance to the spacecraft, a radar-like return pulse would be too weak.2 The ranging system solved this in two ways. First, a complex transponder on the spacecraft sent back an amplified signal. Second, instead of sending a pulse, the system transmitted a long pseudorandom bit sequence. By correlating this sequence over multiple seconds, a weak signal could be extracted from the noise.1

In this blog post I explain this surprisingly-complex ranging system. Generating and correlating pseudorandom sequences was difficult with the transistor circuitry of the 1960s. The ranging codes had to be integrated with Apollo's "Unified S-Band" communication system, which used high-frequency microwave signals. Onboard the spacecraft, a special frequency-multiplying transponder supported Doppler speed measurements. Finally, communicating with the spacecraft required a complex network of ground stations spanning the globe.

The Apollo Service Module's transponder with the lid removed, showing the circuitry inside. The transponder returned the ranging signal to Earth, multiplying the frequency by exactly 240/221.

The ranging system

The ranging system measured how long a signal takes to travel to the spacecraft and back.3 As shown below, the ranging system transmitted a pseudorandom bit sequence to the spacecraft. The spacecraft's transponder returned the signal to the ground receiver. The returned signal was correlated against the original signal to determine the time shift, and thus the distance. Meanwhile, a Doppler measurement (described later) provided the speed of the spacecraft.4

Block diagram of the Apollo ranging subsystem. Redrawn from A study of the JPL Mark I ranging subsystem

The key step was to correlate the transmitted and received signals to determine the time delay. When the two signals were aligned with the proper delay, the bits matched. Because the sequence is pseudorandom, if the two signals were misaligned, the bits didn't match (except randomly).5 Thus, by testing how many bits match (i.e. the correlation) for different delays, the proper delay could be determined. Since the signals could be correlated over long time intervals (multiple seconds), the range could be determined even if the signal was extremely weak and hidden by noise.

The code sequence needed to be very long in order to unambiguously determine the range; the system uses a pseudorandom sequence that is 5,456,682 bits long. Since the code is sent at 1 megahertz, it repeats every 5.46 seconds. A radio signal can travel 800,000 kilometers and back in this time, while the Moon is about 384,000 kilometers away, so the system can unambiguously measure over twice the distance to the Moon. Note that at one megahertz, one bit of the signal corresponds to 150 meters of range. The system achieved more accuracy by comparing the phase of the signals.

Conceptually, the transmitted and received sequences were shifted until they match, and the amount of shift gave the delay, and thus the distance. However, it's impractical to try 5 million different shifts to match the sequence, especially with the technology of the 1960s. To solve the matching problem, the sequence was constructed from several shorter codes, from 2 to 127 bits long. These "sub-codes" were short enough that they could be matched by brute force. The overall delay could then be determined by the delays of the sub-codes. The system used four sub-codes—sub-code A had a length of 31 bits, B was 63 bits, C was 127 bits, and X was 11 bits—along with a two-valued clock CL. Since these lengths are relatively prime, the combined sequence has an overall length equal to the product: 5,456,682. The important concept is that a very long code could be generated and matched using hardware, since the sub-codes were short.

A 30-foot antenna. From Apollo Unified S-Band Technical Conference.

I made an interactive page that demonstrates how the sub-code sequences were created. The sub-code sequences of lengths 31, 63, and 127 were generated with a well-known technique called the linear-feedback shift register (LFSR). In this technique, a shift register of length N holds bits. In each step, a new bit is generated from the exclusive-or of two bits in the shift register. The new bit is shifted in, and an old bit is shifted out, providing a code bit. This technique can generate a pseudorandom sequence of length 2^N-1 with good statistical properties. In order to generate a sub-code of length 11, the X codes were generated from a Legendre sequence.7

The C sub-code is generated from a 7-bit delay line (black). The last two bits are fed into an XOR gate to produce a new bit (red). Part of the pseudorandom sequence is shown below the gate.

Combining the sub-codes to form the overall code isn't as straightforward as you might think, since each sub-code must be individually recognizable in the result. The A, B, and C sub-codes were combined with the majority function maj(A,B,C), which returns the most common bit out of the three inputs.6 The complete formula for the bit sequence was (X·maj(A,B,C))⊕CL.

Construction of the ranging system

The ranging process was implemented by the "Mark I ranging subsystem" below. Although this was called a "special-purpose binary digital computer", it's not really a computer in the modern sense, but more of a state machine that moved through the necessary steps. First, the ground station sent the code sequence to the spacecraft and synchronized to the received signal. Next, the ranging system tested the different offsets for the X sub-code and found the offset with the best correlation. It repeated the process for the A, B, and C sub-codes. The digital circuitry performed some tricky modulo arithmetic8 to compute the range from the sub-code offsets. Finally, the Doppler subsystem determined the spacecraft's speed and constantly added this to the range to keep the range up to date as the spacecraft moved. I've made an interactive page that demonstrates these steps.

The Mark I ranging subsystem. From Apollo Unified S-Band System.

The ranging system was built from "T-Pac modules", boards that used transistors and other discrete components to build simple digital components such as logic gates and flip flops.9 The T-Pac modules were introduced by Computer Control Company in 1958 and were designed for quick and efficient implementation of a digital system, running at 1 MHz. Groups of 32 T-Pac cards were mounted in a "T-BLOC" rack-mounted chassis, and 10 T-BLOCs were installed in two racks. The cards were connected by plugging wires and taper pins into a large grid.

One module was the T-Pac LE-10 "logic element" module, below, implementing four AND gates. It cost $98 in 1961 (about $700 in current dollars), showing how expensive digital logic was at the time. The ranging system used about 300 digital modules, so the digital circuitry for ranging would have cost hundreds of thousands of (current) dollars, a cost repeated at each ground station.

A T-Pac module. This is the LE-10 "logic element".

Tasks that we nowadays consider trivial were difficult with the technology of the time. For instance, the range was stored as a 31-bit binary value. But instead of a register, the value was stored in a magnetorestrictive delay line, as torsion pulses in a long nickel wire. To add a value to the range, the circuitry used a single-bit serial adder, adding bits one at a time as they exited the nickel wire, and then cycling the bits back into the wire.

One interesting circuit is the correlation level detector that tests for correlation between a particular sub-code and the received signal. The correlation started as an analog voltage, which was converted to a digital value by a "Voldicon. The correlation was integrated over time by summing the binary values using another 31-bit storage/adder circuit. The number of summed samples could range from 1 to 2¹⁹ samples, user-settable through "Digiswitch" thumbwheel switches. By integrating the correlation over a long time interval, an extremely weak signal could be detected in the presence of noise. The system kept track of the best offset, storing the value in another delay line. The total ranging time varied from 1.6 seconds for a strong signal to 30 seconds at lunar distance.

Determining the speed with Doppler

The ranging system could also measure the spacecraft's speed by measuring the Doppler shift of the returned signal. If the spacecraft was moving away from Earth, the waves would be stretched out, lowering the frequency. Conversely, the frequency would increase if the spacecraft was moving towards Earth.10 By measuring the frequency shift, the spacecraft's speed could be accurately determined.12

A moving source causes the wavelength to be decreased if the source is moving closer or increased if the source is moving away. Diagram by Tkarcher.

The Doppler measurement impacted the radio system's design in two ways. First, the spacecraft couldn't simply receive and retransmit the signal, because the Doppler shift from the upwards journey would be lost. Instead, a complex frequency-multiplying transponder system was used, so the downlink signal's frequency was exactly 240/221 times the received uplink frequency.11 Second, the spacecraft used phase modulation (PM) instead of the common frequency modulation (FM) for most communication: since frequency modulation changes the signal's frequency, it would have interfered with the Doppler measurements.

The Apollo radio system

Apollo used a complex radio system called the Unified S-Band System that included voice, telemetry, scientific data, television, and the ranging data. These signals were combined and transmitted over a single carrier frequency in the S-band frequency range. The diagrams below show how the spectrum was allocated for the signal up to the spacecraft (transmitted at 2.10640625 GHz), and the down-link spectrum at 2.2875 GHz. These two frequencies are in the exact ratio of 240/221, which turns out to be important. Notice that the voice and data are on fairly narrow subcarriers, while the pseudorandom ranging data has a lower, but very wide spectrum. (The ranging signal looks a lot like white noise due to its randomness.) The wide spectrum makes the ranging signal easier to detect at low levels with noise. Even though the ranging spectrum overlaps with the voice and data subcarriers, they don't interfere too much because the ranging spectrum is spread out.

The spectrum used by the Apollo radio system.

The transponder

The S-band transponder onboard the spacecraft had a critical role in both ranging and for communications in general. From the outside, the transponder (built by Motorola) is a plain blue-gray box, weighing about 32 pounds. The connectors at the right linked the transponder to other parts of the radio system. Internally, the transponder was crammed full of radio circuitry: phase modulators for voice data, a detector for received uplink data, and an FM transmitter for video.14

The S-band transponder.

The block diagram below shows the role of the transponder (red) in the communications system. Once the spacecraft was outside of VHF range (about 1500 miles), all communication used the S-band and went through the transponder. The transponder was connected to a traveling-wave tube amplifier and then the spacecraft's antennas.

Diagram of the communications system used in Apollo. The transponder is highlighted in red. Click this (or any image) for a larger version. From "Apollo Logistics Training", courtesy of Spaceaholic.

The photo below shows a closeup of the circuitry inside the transponder. The transponder is constructed of multiple modules, connected by tiny coaxial cables. The frequency multiplier, mixer, IF amplifier, and wide band detector modules are visible. Most of the modules are duplicated on the other side of the transponder to provide redundancy, since a failure of the transponder would jeopardize the mission.

Closeup of the transponder.

The most complex part of the transponder is how it received the ranging data from Earth and echos it back. To avoid interference, the retransmitted data is at a different frequency from the received data. But in order to preserve the Doppler shift information, the transmitted frequency had to vary with the received frequency, so it couldn't be fixed. Instead, the transponder multiplied the received frequency by exactly 240/221 to generate the retransmission frequency, using a complex phase-locked loop circuit.

A phase-locked loop is a widely-used circuit that allows an oscillator to be locked to another frequency source, even in the presence of noise. It uses a voltage-controlled oscillator whose output is compared to the input. If the output is falling behind, the oscillator is sped up. If the input is falling behind, the oscillator is slowed down. Eventually, the oscillator will lock onto the input signal and will track it. The transponder uses a more complex circuit, so the output frequency tracks a multiple of the input frequency, specifically the output frequency is 240/221× the input (uplink) frequency.15

The transponder was one of many electronics boxes crammed into the Command Module. The diagram below shows its position in the equipment racks.

This diagram of the Apollo Command Module shows the position of the S-band transponder, along with the traveling-wave-tube amplifier and the Apollo Guidance Computer.

The console of the Command Module (below) was extremely complicated, with many controls and switches. The astronauts used the highlighted switches to control the transponder and to turn ranging on and off.

Astronauts controlled ranging through a switch on the console. Diagram from Command/Service Module Systems Handbook p208.

Ground stations

Communication with Apollo required powerful ground stations with large antennas.17 These stations needed to be situated around the world to maintain constant communication with Apollo as the Earth rotated. The three main stations had 85-foot (26-meter) parabolic antennas and were located in Goldstone, California; Canberra, Australia; and Madrid, Spain, part of the Manned Space Flight Network (MSFN). Other stations had smaller 30-foot antennas. Coverage gaps were filled by special ships with 30-foot antennas as well as special Apollo Range Instrumentation Aircraft (ARIA), based on C-135 cargo aircraft.

NASA's 26-meter antenna at Honeysuckle Creek, Australia. Photo from NASA.

The block diagram below gives a hint of the complexity of a ground station, with signal processing equipment as well as computers16 and networking to Mission Control and other sites. The "Ranging Circuitry" block has the most relevance to this discussion, but I'd also like to point out the "angle channel receivers". The antennas were servo-positioned to lock onto the spacecraft's signal. This provided an angle measurement of the spacecraft's position, which was combined with the range to yield the spacecraft's 3-D position in space.

Block diagram of a Unified S-Band ground station. From Apollo Unified S-Band System.

The photo below shows the ground station's transmitter/receiver cabinets that handled the unified S-Band signals. These cabinets were the connection between the microwave equipment (amplifiers and antennas) and the radio-frequency subsystems for voice, data, instrumentation, ranging, and so forth. The photo zooms in on the ranging receiver control panel. This ranging circuitry performed the analog tasks: it demodulated the received ranging signal, tracked the frequency, extracted the clock and the Doppler signal, and measured the correlation. These signals were provided to the digital ranging subsystem described earlier.

The receiver-exciter subsystem of the ground station, with a closeup of the ranging receiver. From Apollo Unified S-Band System.

Conclusion

The ranging system provided the distance to the spacecraft, the Doppler provided the spacecraft's (radial) velocity, and the position of the receiving antenna provided the spacecraft's angular position. The system provides a great deal of accuracy for distance and speed: 1.5-meter range resolution and 0.1 meter/sec speed resolution. Because the angular measurement depended on the physical positioning of the antenna, angular resolution was much worse: 0.025°, which corresponds to over 150 kilometers at the distance of the Moon.

The ranging system illustrates the complexity of Apollo. Even though ranging was a small part of Apollo's navigation, it required complex racks of hardware distributed to sites around the world, specialized algorithms, and an advanced transponder onboard the spacecraft. Almost every part of Apollo has this sort of fractal complexity, where a seemingly-simple requirement such as finding the distance to the spacecraft required numerous innovations. The S-band communication system alone required a 1965 conference with 317 pages of proceedings.

The ranging system is hard to understand from a text description, so I've made two interactive pages that demonstrate it. The first page shows how linear-feedback shift registers (LFSR) and XOR gates generate the subcodes, and how the subcodes create the transmitted signal. The second page shows how the correlations are determined for the various subcodes and how the range is computed from these values.

I've implemented the ranging codes on a Teensy, so the next step is to transmit the codes through an actual Apollo transponder. I announce my latest blog posts on Twitter, so follow me @kenshirriff for updates. I also have an RSS feed. Thanks to Steve Jurvetson for providing the S-band transponder and the traveling-wave tube amplifier. Thanks to Mike Stewart for extensive information on the Apollo hardware and CuriousMarc for driving the transponder restoration.

Notes and references

1. The ranging system has a lot in common with GPS. GPS also works by sending a pseudorandom bit sequence and using correlation to determine the signal's delay. There are several important differences though. First, ranging only determined distance, while GPS determines position in three dimensions and also the exact time. (This is why GPS requires visibility of at least four satellites.)

   Second, the GPS signal is transmitted from a satellite and received on the ground, unlike the Apollo ranging signal which was both transmitted and received on the ground. As a result, the GPS receiver doesn't have the transmitted signal available, but must generate its own copy for comparison.

   Third, GPS satellites are about 20,000 kilometers from Earth, while the Moon is 384,000 kilometers from Earth, making the Apollo signal much weaker. (Although Apollo did have the advantage of huge 26-meter receiving antennas, rather than a GPS antenna that is a few centimeters long.)

   Finally, GPS has the advantage of complex integrated circuits to determine the correlation, rather than racks full of transistor logic.

   As far as I can tell, there isn't any direct connection between the Apollo ranging system and GPS. GPS grew out of the Transit (Naval Navigation Satellite System), the Timation satellite program, and USAF Project 621B (history). ↩

2. A radar signal was first bounced off the Moon in 1946 (details, p 25), but the distance accuracy was only ±1000 miles. The radar return from the spacecraft would be much smaller due to its size. ↩

3. There's a complicated history leading up to the Apollo ranging system. Development of Radar (RAdio Detection And Ranging) started in the 1920s. Radar became critically important in World War II, and to counteract jamming, spread-spectrum ideas were applied. The WHYN missile ranging system (1946) used correlation detection to determine the phase difference and thus range. The Federal Telecommunications Laboratories investigated noise-like signals for communication in 1948. This unusual system stored noise values optically on a rotating disk; curiously, the original source of random numbers was the Manhattan telephone directory. The NOMAC (NOise Modulation And Correlation) system (1952) explored thermal noise as a carrier for communication. The CODORAC (either COded DOppler Ranging And Command or COded Doppler RAdar Command) system at JPL (1952) used similar electronics and became the basis for the Deep Space Instrumentation Facility. It introduced a phase-locked loop (PLL) to cancel out Doppler variations, as well as linear-feedback shift register sequences for "pseudonoise". JPL's continuing research led to the ranging system used for Apollo, as well as the Space Ground Link Subsystem (SGLS) (1966), which is still used by the US Air Force. See The Origins of Spread-Spectrum Communications for more. ↩

4. One complication is that the spacecraft is moving very rapidly during the ranging process, up to 10,000 meters per second. This creates two problems. First, the distance measurement will be out of date by the time it is completed. Second, the bit alignment is shifting many times per second, which makes it hard to find the correlation. The solution was to use separate clocks for the sending and receiving circuitry. The receiver clock was locked onto the signal received from the spacecraft. (Due to Doppler shift, this frequency would be slightly different.) By generating the codes from this clock, the codes stayed exactly aligned even as the spacecraft moved. Integrating the difference between the two clocks provided the change in distance since the start of the measurement. Thus, the computed range remained locked to the distance at the start of the measurement, and the Doppler data gave the incremental distance change. Combining these provided the correct range, continuously updated. ↩

5. The pseudorandom sequence must be carefully designed so non-matches can be clearly distinguished from matches, even in the presence of noise. Specifically, misalignments should have as many mismatched bits as possible. The LFSR and Legendre sequences provided this property. In contrast, the sequence 0000011111 would be a bad choice, since if it is shifted by 1, most of the bits still match. Moreover, the number of mismatches should be constant, regardless of the shift. Otherwise, the correlation may match against a local peak rather than the correct shift.

   For more about the mathematics of correlating codes, see Sequences with Small Correlation ↩

6. The majority function maj(A,B,C) matches the A value 75% of the time (and likewise for B or C), allowing the correlation to be detected. (In contrast, A⊕B⊕C would be a bad choice since it only matches A 50% of the time, so the correlation is essentially random.) For a quick analysis of the majority function, consider maj(A,B,C) where A is 1 and the other inputs have four possibilities: maj(1,0,0)=0, maj(1,0,1)=1, maj(1,1,0)=1, and maj(1,1,1)=1. The result matches a for all except the first case, i.e. 75% of the time. (If a is 0, the analysis is similar.) The majority function can be expressed in Boolean logic as A·B+B·C+A·C, i.e. true if any two inputs are set. ↩

7. The idea of the Legendre sequence is that some numbers have an integer "square root" modulo 11 (technically a quadratic residue), and some do not. For instance, 5² = 25 ≡ 3 modulo 11, so in a sense 5 is the square root of 3. If you take the numbers 0 through 10 and assign 1 if the number has a "square root" and 0 otherwise, you get the X codes. (The ranging sequence is slightly different from the mathematical Legendre sequence, which uses -1 for a "quadratic nonresidue" instead of 0.) ↩

8. The modulo equations were solved using the Chinese remainder theorem, developed by the Chinese mathematician Sunzi Suanjing in the third century. The ranging system used pre-computed numbers that canceled out for all except one sub-code. For instance, 992124 is congruent to 1 modulo 11, but congruent to 0 modulo 31, 63, and 127. Multiplying this number by the X offset provides the X sub-code's contribution to the range.

   The Chinese remainder theorem constants are
   992124 ≡ 1 (mod 11) for the X subcode
   1408176 ≡ 1 (mod 31) for the A subcode
   736219 ≡ 1 (mod 63) for the B subcode
   2320164 ≡ 1 (mod 127) for the C subcode
   These numbers are ≡ 0 modulo the other cases. Thus, the total offset T = 992124×X + 1408176×A + 736219×B + 2320164×C (mod 5,456,682).

   The numbers can be obtained by a straightforward algorithm, described in Appendix E of the NASA document. The numbers were hard-coded into the ranging hardware by a "Chinese Number Generator", logic gates that provided the numbers in serial form for serial addition. ↩

9. The Honeywell DDP-116 minicomputer (1965) also used T-Pac modules. Honeywell acquired Computer Control Co., the manufacturer of T-Pacs, in 1966 to expand their digital capability. The earlier Honeywell DDP-19 was a curious computer since it used 19-bit words; it was built with S-Pac modules. The later µ-Pac modules used integrated circuits in place of transistors. ↩

10. Note that the Doppler system can only measure the spacecraft's velocity towards or away from Earth. Perpendicular motion would not show up. ↩

11. I haven't been able to find any explanation for the specific 240/221 frequency ratio between the transmitted and received frequencies. The two frequencies needed to be different so the transmitted signal doesn't overpower the received frequency. The ratio should be fairly close to 1, though, so the system can be optimized for a particular frequency band. The ratio should be reasonably small integers so frequency multipliers can be used. But the mystery to me is why 240/221 instead of, say, 12/11, which is almost the same but much easier to generate. My current theory is that the larger ratio avoided collisions between harmonics that would otherwise occur. (e.g. 12×f1 = 11×f2, which might distort the received signal?) ↩

12. The code delay and the Doppler shift aren't independent, but are really two aspects of the same thing. For example, suppose the spacecraft is moving away at 15 meters/second. This will stretch the radio waves, decreasing the frequency. The 1 MHz pseudorandom signal transmitted to the spacecraft will return with each 1-microsecond interval stretched by 0.1 picoseconds.13 In 10 seconds, the ranging system will transmit 10 million pulses, so the Doppler stretching will cause the pulse train to be 1 microsecond longer, one pulse. The other way of looking at this is that after 10 seconds, the spacecraft will be 150 meters further away, increasing the round-trip signal delay by 1 microsecond. The signal delay from the Doppler shift is the same as the signal delay from the change in range because they are both caused by the spacecraft's motion. ↩

13. Note that the signal transmitted from the ground will be Doppler-shifted when received by the spacecraft, and then the spacecraft's signal will be Doppler-shifted again when received on Earth, so the total Doppler shift is doubled. ↩

14. The block diagram below shows the main components of the transponder. It consists of two phase-modulation transmitter/receivers (for redundancy). At the bottom is the FM transmitter for television signals (not redundant). The VCO (voltage-controlled oscillator) is phase-locked to the input signal, but multiplies the frequency by 240/221. This multiplication is done through several frequency multipliers and mixers. The ranging signal is extracted, phase-modulated at the new frequency, and sent to the antenna for transmission back to Earth.

    

    Block diagram of the transponder. (Click for a larger version.)

     ↩

15. The transponder multiplies the received carrier frequency by 240/221. The Command Module used an uplink frequency of 2106.4 MHz, multiplied by 240/221 for the downlink frequency of 2287.5 MHz, although this can vary by ±120 kHz due to Doppler shift. The Lunar Module and Saturn rocket used an uplink carrier of 2101.8 MHz, multiplied by 240/221 for the downlink carrier of 2282.5 MHz.

    The 240/221 ratio was obtained by a complex process of mixers and frequency multipliers, as shown in the block diagram above. A voltage-controlled oscillator (VCO) in the transponder, ran at a frequency of approximately 19.0625 MHz and formed part of the phase-locked loop. The VCO signal was multiplied by 108 (12×9 in two steps) and mixed with the uplink signal received from Earth. The mixer yielded a signal whose frequency was the difference between the ground signal and the multiplied VCO signal, approximately 47.65625 MHz. A second mixer mixed this signal with two times the VCO frequency, yielding a signal at the difference frequency 9.53125 MHz. The VCO was then phase-locked to this signal to produce an output at twice its frequency, yielding the 19.0625 MHz VCO frequency. Putting this all into an equation:
    (Uplink - 108×VCO - 2×VCO)×2 = VCO
    which simplifies to VCO frequency = Uplink frequency * 2 / 221.

    Meanwhile, the transponder's transmitter multiplied the VCO frequency by 4 to yield a 76.25 MHz carrier. This was multiplied by 30 to yield the 2287.5 MHz downlink frequency. In other words, the VCO frequency was multiplied by 120 to transmit, so the transmitting frequency is 240/221 × Uplink frequency. Thus, the 240/221 frequency ratio is established by multiple frequency multipliers and mixers.

    But how was frequency multiplication implemented? Based on other Apollo circuits, I think the signal was fed into a step recovery diode, a special diode with very fast switching. This turned each input cycle into a sharp pulse, full of harmonics at multiples of the input frequency. A resonant network concentrated the energy at the desired harmonic, and then a filter removed unwanted frequency sidebands. The frequency of the resulting signal was at the desired multiple of the input signal. This process is described in Hewlett-Packard application note 920 (1968).  ↩

16. The ground stations used Univac 642B computers, a 30-bit computer with 32-kilowords of magnetic core storage. The computer was designed for military real-time applications. This computer was a key component of the Naval Tactical Data System, a groundbreaking 1960s system to manage combat information on US Navy ships.

    

    The Univac 624B computer. From Apollo Unified S-Band System.

     ↩

17. For details on the S-band system and ground stations, see Apollo Unified S-Band System. See A study of the JPL Mark I ranging subsystem for a detailed discussion of the ranging hardware. ↩

Reverse-engineering the LM185 voltage reference chip and its bandgap reference

Many circuits, such as a computer power supply or a phone charger, require a stable voltage reference, but it's harder than you might expect to keep a voltage stable when the temperature changes. One integrated circuit that does this is the LM185.1 I looked at the die of this chip and found some interesting features. The same silicon die is used for three different integrated circuits, using tiny internal fuses to change its functionality. The chip uses a special circuit called the bandgap reference to keep the voltage stable even if the temperature changes. In this blog post, I'll discuss the circuitry of the LM185 and its implementation in silicon.

Composite die photo of the LM185. Click this (or any other) image for a larger version.

The photo above shows the LM185 die under the microscope, a tiny square of silicon. The underlying silicon is blue-gray, while the metal wiring on top is orangish. Regions of the silicon are doped with various impurities to form the transistors, resistors, and other devices on the chip. The variations in doping are visible as slight color changes in the silicon. At the top is the National Semiconductor logo.

The LM185 is available in three variants. The LM185-ADJ is the adjustable voltage reference. It has three pins: one is a feedback pin that controls the voltage. The LM185-1.2-N is a two-pin device, called a "micropower voltage reference diode". It is similar to a Zener diode providing 1.235V, but with better performance. (Lower power consumption, less noise, and better stability.) Finally, the LM185-2.5-N provides a 2.5V reference. The three variants are based on the same silicon die. The latter two have the feedback wired internally to provide a fixed voltage rather than an adjustable voltage.

The next sections describe how the various components of the chip are fabricated from silicon, and how they appear on the die.

NPN transistors

The photo below shows a closeup of one of the transistors in the LM185. The black lines and slightly different tints in the silicon indicate regions that have been doped to form N and P regions. The whitish areas are the metal layer of the chip on top of the silicon—these form the wires connected to the collector, emitter, and base.

Structure of an NPN transistor on the die. I edited the transistor layout so a cross-section would work.

Underneath the photo is a cross-section drawing illustrating how the transistor is constructed. There's a lot more than just the N-P-N sandwich you see in books, but if you look carefully at the vertical cross-section below the 'E', you can find the N-P-N that forms the transistor. The emitter (E) wire is connected to N+ silicon. Below that is a P layer connected to the base contact (B). And below that is an N+ layer connected (indirectly) to the collector (C).

The output transistor (below) is much larger than the other transistors and has a different structure in order to support the chip's high-current output. It has multiple interlocking "fingers" for the emitter and base, surrounded by the large collector.

A large, high-current NPN output transistor in the LM185 chip. The collector (C), base (B) and emitter (E) are labeled.

PNP transistors

You might expect PNP transistors to be similar to NPN transistors, just swapping the roles of N and P silicon. But for a variety of reasons, PNP transistors have an entirely different construction. They consist of a small circular emitter (P), surrounded by a ring-shaped base (N), which is surrounded by the collector (P). This forms a P-N-P sandwich horizontally (laterally), unlike the vertical structure of the NPN transistors.

The diagram below shows one of the PNP transistors in the LM185, along with a cross-section showing the silicon structure. Note that although the metal contact for the base is on the edge of the transistor, it is electrically connected through the N and N+ regions to its active ring in between the collector and emitter.

A PNP transistor in the LM185 chip. Connections for the collector (C), emitter (E) and base (B) are labeled, along with N and P doped silicon. The base forms a ring around the emitter, and the collector forms a ring around the base.

Resistors

Resistors are a key component of analog chips. Unfortunately, resistors in ICs are large and inaccurate; the resistances can vary by 50% from chip to chip. Thus, analog ICs are designed so only the ratio of resistors matters, not the absolute values, since the ratios remain nearly constant. The photo below shows two paralleled resistors. Other resistors have a zig-zag shape to fit a longer resistor into the available space.

A resistor inside the LM185 chip. The resistor is a strip of P silicon between two metal contacts.

Capacitors

A capacitor consists of a metal plate on top of silicon, separated by a thin oxide layer that acts as a dielectric. Capacitors are fairly large on integrated circuits; they are the most visible components on this die. The capacitor below contains multiple circular patterns. These may be doped silicon regions, where the junction between two regions provides additional capacitance.

A capacitor on the die.

Fuses

Fuses allow the circuitry of the chip to be changed after manufacturing. The LM185 uses fuses for two reasons. First, fuses can add or remove resistance, allowing the circuit to be tuned for higher performance. Second, a fuse changes the feedback circuitry between the LM185-1.2-N and LM185-2.5-N variants. (The LM185-ADJ version requires more changes than are supported by fuses, so it needs some changes to the metal layer. For instance, it has three pads connected instead of two.)

A fuse has two metal pads attached. Before the chip is packaged, probes can contact the pads and apply a high current to blow the fuse. The first type of fuse is implemented with a tiny strip of metal that is vaporized to break the circuit, just like a large-scale fuse. The second type of fuse is an "antifuse", which has the opposite behavior: it does not conduct until a high current is applied, at which point it becomes conductive. The antifuse can be built from a Zener diode, and the process of shorting it out is called a "Zener zap". The high current forms metal spikes through the junction, causing it to permanently conduct. The diagram below shows a fuse and an antifuse as they appear on the die.

A fuse and an antifuse on the die (I think). The contacts originally had more metal, but I used acid to clean gunk off the die and it dissolved some of the metal.

IC circuit: The current mirror

There are some subcircuits that are very common in analog ICs, but may seem mysterious at first. The current mirror is one of these. The idea is you start with one known current and then you can "clone" multiple copies of the current with a simple transistor circuit, the current mirror.

The following circuit shows how a current mirror is implemented with three identical transistors.2 A reference current passes through the transistor on the right. (In this case, the current is set by the resistor.) Since all the transistors have the same emitter voltage and base voltage, they source the same current, so the currents on the left match the reference current.

Current mirror circuit. The currents on the left copy the current on the right.

A common use of a current mirror is to replace resistors. As explained earlier, resistors inside ICs are both inconveniently large and inaccurate. It saves space to use a current mirror instead of multiple resistors whenever possible. Also, the currents produced by a current mirror are nearly identical, unlike the currents produced by two resistors.

Interactive chip explorer

To illustrate how the components form the chip, the die photo and schematic below are interactive. Click on a component in the die or schematic, and a brief explanation of the component will be displayed.

Click the die or schematic for details...

Because the three variants of the LM185 are slightly different, I had to combine three schematics to form the schematic above. Red components are only in the LM185-ADJ, green components are in the LM185-1.2-N, blue components are in the LM185-2.5-N, and cyan components are in the latter two chips. Note that the primary difference is the feedback circuit, but there are additional differences as well.

How a bandgap reference works

The main problem with producing a stable voltage from an IC is that the chip's parameters change as temperature changes. The bandgap voltage reference is commonly used to create a temperature-independent voltage reference.5 The trick is that it has one voltage that goes down with temperature and another than goes up with temperature. If you combine them correctly, you get a voltage that is stable with temperature.

To create a voltage that goes down with temperature, you can put a constant current through the transistor and look at the voltage between the base and emitter, called V_be. The graph below shows how this voltage drops as the temperature increases. At the left, the line hits the bandgap voltage of silicon, about 1.2 volts; this will be important later.

Vbe vs temperature for a transistor

If you set up a second transistor this way but with a lower current3, you get the same effect but the voltage V_be curve drops faster. This may not seem helpful since we need a voltage that goes up with temperature. But here's the trick: if you subtract the two V_be voltages, the difference increases as temperature increases, since the lines get farther apart. The difference is called ΔV_be. The graph below shows the V_be curves for two different transistors, and you can see how the difference ΔV_be between the curves increases with temperature, even though both curves decrease with temperature.

Voltages in a bandgap reference: Vbe for two transistors as temperature changes.

The final step to a bandgap reference is to combine V_be and ΔV_be in the right ratio so the result is constant with temperature. It turns out that if the values sum to the bandgap voltage of silicon (approximately 1.2 volts), the drop in V_be and the increase in ΔV_be cancel out. In the graph below, adding 10 copies of ΔV_be is the right ratio; the exact ratio depends on the particular transistors. The important thing to notice in the graph below is that as the temperature changes, V_be+nΔV_be remains constant - the top of the blue ΔV_be line remains at the bandgap voltage.

By adding multiples of ΔVbe to Vbe, the bandgap voltage is reached regardless of temperature.

In the LM185, the key transistors are Q10 and Q11, where Q10 has 10 emitters in parallel, so each has 1/10 the current. Thus, if you feed the same current into both transistors, Q10 has a lower V_be voltage than Q11 as described above. Note that Q10 is split in two: one half above Q11 and one half below Q11. This layout minimizes potential error due to a temperature gradient across the die. Half of Q10 will be hotter than Q11 and half will be cooler, so the difference will cancel out.

Transistors Q10 and Q11 are the key to the bandgap reference. Q10 has 10 emitters, so each has 1/10 the current as Q11.

The diagram below shows how the bandgap reference is implemented in the LM185. Transistors Q10 and Q11 have different V_be voltages due to their relative sizes. The difference in these voltages (ΔV_be) is developed across R7. Since the same current flows through R6, R7, and R8, the voltage across R6 will be 4ΔV_be and the voltage across R8 will be 6ΔV_be by Ohm's law. Thus, the combination of R6, R7, and R8 multiply ΔV_be by 11. Meanwhile, Q14 has its own V_be.

The bandgap circuit in the LM185.

Summing the voltages along the right gives V_be + 11ΔV_be, which is designed to match the temperature-stabilized bandgap voltage of 1.2 volts. Thus, the circuit will be balanced4 if the voltage between the feedback input and V+ is 1.2 volts. If the voltage is not 1.2 volts, Q10 and Q11 will pass different amounts of current. Since the current mirror (Q12 and Q13) attempts to feed the same current into Q10 and Q11, any discrepancy will appear as current at the error output. This error current is amplified and controls the output transistor, adjusting the voltage until the feedback voltage is brought back into compliance. Thus, the circuit maintains the desired voltage, stabilized even if the temperature changes.

Conclusion

Well, that turned into a longer blog post than I was expecting. Although the LM185 doesn't contain many components by modern standards, it provides a stable, regulated voltage reference. It has some interesting features such as the use of fuses both to improve performance and to sell variant chips. It also illustrates the principle of the bandgap voltage regulator.

I announce my latest blog posts on Twitter, so follow me @kenshirriff. I also have an RSS feed. Thanks to Mitch Wright for supplying the chip.

Notes and references

1. The LM185, LM285, and LM385 are the same chip, but with different temperature ranges. The LM185 is rated for the military temperature range: -55°C to 125°C. The LM285 is rated for the automotive temperature range: -40°C to 85°C. The LM385 is rated for the standard temperature range: 0°C to 70°C. I believe the chips are identical except for testing. For the purposes of this post, you can treat the three chips as identical. ↩

2. For more information about current mirrors, check Wikipedia or chapter 3 of Designing Analog Chips. ↩

3. When building a bandgap reference, what really matters for V_be is the current density through the transistors - the current divided by the area of the emitter. Decreasing the current through the transistor decreases the current density. The second way to decrease current density is to use a larger transistor with a larger emitter. Often five or ten identical transistors in parallel will be combined to form this large transistor to ensure the large transistor and the small transistor are exactly matched. ↩

4. One tricky thing about the bandgap circuit is that it is implemented "backward", taking the voltage as an input. The chip's block diagram6 shows that the reference generates 1.2 volts and this is compared to the input voltage. But in reality, the input voltage is fed into the bandgap circuit. If the input is 1.2 volts, the circuit is balanced. But if the input is too high or too low, the bandgap circuit will be unbalanced with more current through one transistor than the other. This "error" signal is amplified and used as feedback to adjust the input voltage until it matches 1.2 volts. In other words, there's no 1.2-volt reference inside the chip. Instead, the chip and its external input form a feedback loop that generates 1.2 volts. ↩

5. I've written before about bandgap references, specifically the 7805 voltage regulator and the TL431. ↩

6. The TL431 is a popular voltage reference, used in many power supplies. The main difference is that the LM185 regulates the voltage relative to the positive side, while the TL431 regulates the voltage relative to the negative side.

   

   Comparison of the LM185 and TL431 block diagrams, from the datasheets.

    ↩

Reverse-engineering a mysterious Univac computer board

The IBM 1401 team at the Computer History Museum accumulates a lot of mystery components from donations and other sources. While going through a box, we came across the unusual circuit board below. At first, it looked like an IBM SMS (Standard Modular System) card, the building block of IBM's computers of the late 1950s and early 1960s.1 However, this board is larger, has double-sided wiring, the connector is different, and the labeling is different.2

The circuit board is about 15cm×7.3cm.

I asked around about the board and Robert Garner identified it as from the Univac 1004, a plugboard-controlled data processing system from 1963.4 The Univac 1004 was marketed as a "Card Processor" rather than a computer,3 designed for business applications that read punch cards and producing output, but still required calculation and logical decisions. Typical applications were payroll, inventory, billing, or accounting.

Photo of the Univac 1004. From bitsavers.

The most unusual feature of the Univac 1004 was that it was programmed by a plugboard (below) instead of a stored program. The system was programmed by plugging patch cords into a plugboard to indicate the desired action for each of the 31 program steps. While earlier electromechanical accounting machines used plugboards, they were pretty much obsolete by 1963, so I was a bit surprised to see plugboards still in use.

A plugboard for the Univac 1004. This board was used for payroll consolidation from 1965 to 1972. From Museums Victoria Collections, Copyright Museums Victoria / CC BY 4.0.

The computer's "program" consisted of 31 steps. The operations for each step were specified by plugging wires into the board. For instance, a data field could be moved from a punch card to memory, a value could be added or subtracted, or a line of output could be configured for the printer.5 The system even supported conditional branches. The diagram below shows the structure of the plugboard. The highlighted wire shows a subtraction operation, activated by the wire in the "algebraic minus" position.

Part of a program in the plugboard. Click for a larger version. From the Reference Manual.

The computer had a small memory of 961 6-bit characters. Like most computers of the era, it used magnetic core memory, storing each bit by magnetizing a tiny ferrite ring. Note that since the computer was programmed through a wiring panel, none of the memory was used for program code.

A plane of magnetic core storage, from the Reference Manual.

While the Univac 1004 was primitive for its time compared to even a low-end business computer like the IBM 1401, it had a few advantages. First, it rented for $1900 a month, compared to $2500 a month for the IBM 1401 (about $18,000 vs $23,000 a month in current dollars). Second, the Univac computer was compact (by 1960s standards), weighing 2500 pounds. Finally, many customers found plugboard programming easier than programming with code, both because they were more familiar with it and because it is visual and direct.

The Univac 1004 could be extended with peripherals such as tape drives, a card punch, or disk storage. The photo below shows the Unidisc cartridge, which held one million characters. Although it looks like an absurdly-large floppy disk, it was a removable hard disk.

The Unidisc cartridge is 15¾ inches square and ⅝-inch thick. (source).

Reverse-engineering the board

The function of the board wasn't immediately obvious and we had various theories of what it might do. To find out, I reverse-engineered the board by tracing out the circuitry.6 The board has 32 diodes, which seems like a lot, as well as resistors, transistors, and capacitors. The transistors are not silicon transistors, but germanium PNP transistors.

A closeup of the circuit board showing resistors and diodes.

The board turned out to be a logic board implemented with AND-OR-INVERT logic.7 That is, various inputs are ANDed together, the AND results are then ORed together, and finally the result is inverted. The board is implemented with diode-transistor logic. One layer of diodes implements the AND gates and the second layer of diodes implements the OR gates. Finally, a transistor amplifies the result, inverting it in the process. Diode-transistor logic (DTL) performed better than earlier resistor-transistor logic (RTL), but was soon replaced by transistor-transistor logic.

The diagram below explains how the AND-OR-INVERT logic was implemented. This circuit has four inputs: two AND gates that are then ORed together and inverted. (It's a bit confusing because the circuit uses active-low logic, so the voltage levels are all inverted.) If the AND gates all have a 0 (high) input, a diode in the first stage will conduct and pull the AND node high. This blocks the diodes in the second stage (which have the opposite orientation), so the OR node is also high. In the INVERT stage, the +20V resistor will pull the transistor's base high, which turns it off (since it is PNP). Finally, the -8V resistor will pull the output low (i.e. 1), providing the desired AND-OR-INVERT logic.

The AND-OR-INVERT logic producing a 1 output.

The diagram below shows that if the first AND gate's inputs are 1 (low), the first diodes are blocked, so the -30V resistor pulls the AND node low (1). Now the second-stage diode conducts, pulling the OR node low (1). This allows base current to flow through the PNP transistor, turning it on. This pulls the output high (0). (Note that ground is a high output compared to the low output of -8V.) The gates on the board have more inputs, but use the same principle.

The AND-OR-INVERT logic producing a 0 output.

After tracing out the board's logic, I recognized that it implemented a full adder.8 That is, it adds two input bits along with a carry-in, producing a sum bit and a carry-out. By connecting four full-adders in series, a 4-bit value can be added, allowing one decimal digit to be added. Thus, the computer probably has four one-bit adder boards similar to this, along with circuitry to convert the output from binary to binary-coded decimal.10

The board has a few additional circuits along with the full adder circuit. It includes an inverter circuit. The board also has 4 inputs that are ANDed, subject to the carry value. Finally, the board also has a disable input that blocks the outputs.9 Without knowing more about the circuitry, I can't determine the role of these circuits.

Conclusion

The mystery circuit board turned out to be from the Univac 1004. Although this computer was produced in the 1960s, its technology occupies an interesting location between the electro-mechanical accounting machines of the 1940s and the electronic business computers of the late 1950s. The Univac computer used transistors and core memory, but it kept the earlier plugboard programming of the accounting machines, rather than moving to stored-program computing (introduced in 1948). Even though the Univac 1004 was technologically backward for 1963, businesses flocked to it, making it the second-most popular computer at the time with 3400 installations.4

This shows that progress isn't as linear as you might expect; "obsolete" technologies can continue to thrive long after the introduction of "superior" alternatives such as stored-program computing. Instead, new systems can still be developed with supposedly-obsolete technologies, depending on the tradeoffs involved.

I announce my latest blog posts on Twitter, so follow me @kenshirriff. I also have an RSS feed.

Notes and references

1. The Computer History Museum links to a similar board. ↩

2. The photo below compares the Univac board to a smaller IBM SMS board.

   

   Comparison with an IBM SMS card.

    ↩

3. The Univac 1004 computer came in two versions. The "80" read standard IBM 80-column punch cards. The "90" read Univac's 90-column cards (details), which held 90 characters per card instead of 80. The 90-column card was introduced in 1930 by Remington Rand. It had round holes instead of IBM's rectangular holes. The card stored two characters per column by using a denser, binary code. Despite the superior capacity of the 90-column card, IBM's 80-column cards dominated the market. (Even IBM couldn't displace the 80-column card, although they tried with the 96-column card that they introduced in 1969.)

   

   A 90-column punch card. From Marcin Wichary, (CC BY 2.0).

    ↩

4. Robert Garner discusses the Univac 1004 briefly in his article on Early Popular Computers. More information is in the 1964 BRL report as well as on Bitsavers. A related board from the Univac 1040/1050 is described here. ↩↩

5. The plugboard supported conditionals and looping, so I think the system was Turing-complete, although you couldn't do a lot in 31 programming steps. You could implement multiplication or division with a short shift and add (or subtract) loop. ↩

6. To reverse-engineer the board, I took photos of both sides, flipped the image of the back in GIMP so the two sides were aligned visually, arranged the components on a schematic in EAGLE, and connected the components to match the circuit board. Then I moved the components around until the layout made sense.

   

   The underside of the circuit board.

   The back of the circuit board is shown above. Note that the edge connectors are completely different on the two sides of the board.

    ↩

7. AND-OR-INVERT logic was also used in the IBM System/360 computers, although it was built from hybrid SLT modules instead of discrete components. ↩

8. I suspected the board was an adder when I saw that it had three inputs and was combining them symmetrically. The full adder is implemented in AND-OR-INVERT logic as follows. If the two bits are A and B and the carry-in is CIN, then a carry-out (COUT) is generated if at least two input bits are set. This is computed by the AND-OR logic "(A and B) or (A and CIN) or (B and CIN)". The sum bit is set if there is a single 1 input or three 1 inputs. The sum bit was computed by "(A and not COUT) or (B and not COUT) or (CIN and not COUT) or (A and B and CIN)" As a result of the AND-OR-INVERT circuit, the output is inverted. The inverter circuit on the board was probably used to un-invert it. ↩

9. The full reverse-engineered schematic is below.

   

   Reverse-engineered schematic of the board. Click for a larger version.

    ↩

10. The computer uses excess-three encoding for digits, adding 3 to the value before converting to binary. For example, 6 is represented as binary 1001. The advantage of this encoding is that flipping the bits yields the 9's-complement decimal value, simplifying subtraction. For example, flipping the bits of 6 yields binary 0110, which is 3 in excess-3 notation. Excess-3 representation also handles carries correctly; if you add two numbers that sum to 10, the excess-3 values will sum to 16, causing a binary carry. To convert the sum to excess-3, The value 3 must be added (if a carry) or subtracted (if no carry).

    To see how addition works with excess-3, 2 + 4 in excess-3 is binary 0101 + 0111 = 1100. Subtracting 3 yields 1001, which is 6 in excess-3. But 2 + 9 is binary 0101 + 1100 = 10001, generating a carry out of the 4 bit value. Adding 3 yields 0100, which is 1 in excess-3. Considering the carry-out, this is the desired result of 11. ↩