Yamaha DX7 chip reverse-engineering, part 6: the control registers

The Yamaha DX7 digital synthesizer (1983) was the classic synthesizer in 1980s pop music. It uses a technique called FM synthesis to produce complex, harmonically-rich sounds. In this blog post, I look inside its custom "OPS" sound chip and explain the control registers for this chip. By reverse-engineering the circuitry, I found a few undocumented test functions. (This post covers some fairly obscure details of the DX7; you might prefer my previous DX7 posts1 starting with "DX7 reverse-engineering".)

Die photo of the YM21280 chip with the main functional blocks labeled. Click this photo (or any other) for a larger version.

The die photo above shows the DX7's OPS sound synthesis chip under the microscope, showing its complex silicon circuitry. Unlike modern chips, this chip has just one layer of metal, visible as the whitish lines on top. Around the edges, you can see the 64 bond wires attached to pads; these connect the silicon die to the chip's 64 pins. In this blog post, I'm focusing on the control registers, highlighted in red. I'll outline the other functional blocks briefly. Each of the 96 oscillators has a phase accumulator used to generate the frequency. The sine and exponential functions are implemented with lookup tables in ROMs. Other functional blocks apply the envelope, hold configuration data, and buffer the output values.

The DX7 synthesizer. Photo by rockheim (CC BY-NC-SA 2.0).

The DX7 generates sounds digitally using a technique called FM synthesis. Each note has six oscillators (called "operators") that can be combined in different ways (called "algorithms"). An algorithm is represented by a diagram (below), where an oscillator modulates the oscillator below, as shown by the lines. For instance, in algorithm 1 below, oscillator 6 modulates oscillator 5 which modulates 4 which modulates 3. Oscillator 2 modulates oscillator 1. The output is taken from the bottom oscillators (1 and 3). Meanwhile, oscillator 6 modulates itself, controlled by a user-selectable feedback level. With 32 different algorithms, the DX7 can generate a wide variety of sounds. In the DX7 synthesizer, all 16 notes must use the same algorithm. But from my reverse-engineering, it appears that the chip supports different algorithms for each note, even though the synthesizer doesn't make use of this.

Four of the 32 "algorithms" that can be selected on the DX7.

To the programmer of the DX7 firmware, the sound chip appears to have two write-only registers that control the chip. The diagram below shows the layout of the chip's s two registers, as described by Anthony Richardson. The desired algorithm and feedback are written to address 1.2 Address 0 has bits to turn the "key sync" feature3 on and off. As for the Mute and Test Register Select bits, my investigation provides some explanation.

Address | Bit 7 | Bit 6          | Bit 5        | Bit 4 | Bit 3 | Bit 2 | Bit 1 | Bit 0 |
0       | Mute  | Clear Key Sync | Set Key Sync | Test Register Select                  |
1       | Algorithm Select (0..31)                              | Feedback Level (0..7) |

(The functionality above is pretty limited, so you might wonder how the synthesizer controls which notes are played. Most of the synthesizer functions are controlled through a second custom chip, the envelope generator chip (EGS). Note and envelope data is written to registers in the EGS chip, which then sends frequency and amplitude data to the sound chip over a special bus.)

The diagram below shows the main components of the register circuitry. The large block at the bottom is the A-register, which holds the algorithm/feedback entries, as 16 8-bit values.4 The most puzzling feature of the A-register is its size; it holds 16 entries, one for each note, but the DX7 uses the same algorithm/feedback setting for all 16 notes. The second puzzling feature is that although the chip appears to have two 8-bit registers, the implementation is one 9-bit register, and one 5-bit register. Moreover, the 5-bit register can only be modified by writing through the 9-bit register.

Main functional blocks of the register circuitry.

The chip has one address pin (called "DS") which selects between the two registers. When a byte is written to the chip, to either address, the 8 bits along with DS (the address bit) are stored in the 9-bit latches. If DS is 0 (i.e. write to the control address 0), the bits are decoded to perform any special functions, and the lower 5 bits are loaded into the 5-bit register on the right. If DS is 1 (i.e. write to the algorithm/feedback address 1), the 8-bit algorithm/feedback value is stored into the A register, in a location controlled by the 5-bit register.

Updating the algorithm/feedback

The algorithm/feedback A-register register holds data for 16 notes. It can be updated in two ways. The first way, used by the DX7, updates all entries with the same value. The second way updates a single entry, allowing different notes to have different algorithms. Both cases involve a write to address 0, followed by writing the algorithm/feedback byte to address 1.

To update all entries, address 0 must be written with a value with the bit pattern 0??1?0?? (where ? indicates a "don't care" bit that can be 0 or 1).5 This pattern triggers a circuit that constantly loads the value in the data latch into the storage register.

The DX7's CPU controls the OPS chip in this way. Specifically, an update of the algorithm and feedback is performed by writing either 0x30 (if sync is on) or 0x50 (if sync is off) to address 0, and then writing the algorithm/feedback byte to address 1.2

The second update path will change the algorithm and feedback for a single note. (The DX7 does not use this feature.) is triggered by writing the bit pattern 0??0nnnn, where nnnn specifies one of the 16 notes.

The implementation of this is a bit tricky because the chip uses shift registers for storage, not RAM. The A-register consists of 8 shift registers (one for each bit), each with 16 stages (one for each note). An entry can only be updated when it is shifted out the end of the shift register, and a new value can be inserted. (This is unlike RAM, where an arbitrary entry can be written.) To update an entry in the shift register, a 4-bit comparator circuit (below) compares the number of the current note with the number of the desired note in the control register. When there is a match, the new value is written to the shift register.

The 4-bit comparator determines when the shift register is at the desired note position. It is built from four exclusive-NOR gates.

Special command sequences

The logic circuitry recognizes several bit patterns when they are written to address 0, and causes special actions when they are detected. These are not used by the DX7; I think they were used for testing the chip during manufacturing to make tests more predictable and faster.

1???????: Setting the top bit triggers several special actions. Earlier analysis has labeled this bit as "Mute", but I suspect it is more of a "Test Reset" function, resetting the chip to a known state so tests will be predictable. This bit clears the phase accumulators. This bit disables the scale factors, so the output data is unshifted. It also bypasses the output latch, which may output digital note data at a higher rate.

1??????1: In addition to the previous action, this pattern resets the counters that count through the operators and notes, controlling the actions of the chip. This is probably used start testing the chip from a known state, so the outputs can be compared with expected values.

1?????1?: This causes the low-order bits of the phase register to generate the waveform, rather than the high-order bits. I think this is used for testing so the low-order bits can be examined more directly to find flaws. It also will increase the frequencies by a factor of 1024, which may help run through waveforms faster for testing.

Conclusion

By looking inside the chip and reverse-engineering the silicon circuits, I learned some details about the internal registers. One interesting discovery is that the chip appears to support separate algorithms for each voice, even though the synthesizer doesn't use this feature. I also uncovered some test functionality.

The Yamaha YM21280 OPS integrated circuit package with the metal lid removed, revealing the silicon die.

I plan to continue investigating the DX7's circuitry, so follow me on Twitter @kenshirriff for updates. I also have an RSS feed. Thanks to Jacques Mattheij and Anthony Richardson for providing the chip and discussion.6

Disclaimer: I figured out the behavior described in this post studying the die. It hasn't been tested on an actual DX7 so I don't guarantee that it is correct.

Notes and references

1. My previous posts on the DX7: DX7 reverse-engineering, The exponential ROM, The log-sine ROM, How algorithms are implemented, and The output circuitry. ↩

2. Looking at the ROM shows how the synthesizer's CPU communicates with the OPS chip. Since the DX7 ROM code has been disassembled, you can view the code that writes to the sound chip here. ↩↩

3. Oscillator Key Sync is a feature of the DX7. According to the manual, Operator Key Sync "enables you to set the operator so its 'oscillator' begins at the start of the sine wave cycle each time you play a note. When Oscillator Key Sync is off, the sine wave continues so that subtle differences will occur even when you play the note repeatedly." ↩

4. The DX7/9 Service Manual shows the "A-register" holding the algorithm and feedback level, so I'll use that name. ↩

5. The bit pattern 0??1?0?? looks a bit random. I don't know why this pattern was chosen. The first two bits can be explained, but I don't see a purpose for the last 0 bit. ↩

6. For more information on the DX7 internals, see DX7 Technical Analysis, DX7 Hardware, OPLx decapsulated, and the video Emulating the DX7 the hard way. ↩

Yamaha DX7 chip reverse-engineering, part V: the output circuitry

The Yamaha DX7 digital synthesizer (1983) was the classic synthesizer in 1980s pop music. It uses a technique called FM synthesis to produce complex, harmonically-rich sounds. In this blog post, I look inside its custom sound chip and explain how the chip's output circuitry works. You might expect it's just a digital output fed into a digital-to-analog converter, but there's much more to it than just that.

Die photo of the YM21280 chip with the main functional blocks labeled. Click this photo (or any other) for a larger version.

The composite die photo above shows the DX7's OPS sound synthesis chip under the microscope, revealing its complex silicon circuitry. Unlike modern chips, this chip has just one layer of metal, visible as the whitish lines on top. Around the edges are the 64 bond wires attached to pads; these connect the silicon die to the chip's 64 pins. The three blocks in red are the focus of this post. The output buffers hold the 16-bit digital values for the 16 notes. The output is controlled by a counter and PLA (Programmable Logic Array). The synthesizer's digital-to-analog conversion uses a sample-and-hold circuit, controlled by the "S/H ctrl" block.

I've discussed the chip's other functional blocks in earlier posts1, so I'll just give a brief summary here. Each of the 96 oscillators has a phase accumulator used to generate the frequency. The oscillators are combined using the operator computation circuitry in the middle of the chip, under the control of the algorithm ROM. The signal synthesis uses sine and exponential functions, implemented with lookup tables in ROMs.

The Yamaha DX7 synthesizer with its 61-key keyboard and digital controls. Photo by rockheim (CC BY-NC-SA 2.0).

The synthesizer's output circuitry

Before I dive into the details of the chip, I'll explain the synthesizer's output circuit. The heart of the synthesizer is the OPS (Operator S) sound chip that digitally generates the notes. It provides digital values to the digital-to-analog converter (D/A). The resulting analog signal goes through a low-pass filter (LPF). The volume is controlled by a foot pedal and the synthesizer's volume control. Finally, the signal is amplified for the line and headphone outputs.

Block diagram of the output circuit. Based on the DX7/9 Service Manual.

The digital-to-analog conversion is more complex than you might expect. The process starts with the digital-to-analog converter (DAC) chip2 that takes a 12-bit digital value from the sound chip and converts it to an analog value in the range 0 to 15 volts.3 The multiplexer allows the overall synthesizer volume to be controlled by MIDI, but with just 8 levels.

Schematic of the volume control and DAC circuit. Based on the DX7 schematics.

The DAC provides 12 bits of resolution, but an additional circuit (below) provides approximately two more bits. This scaler circuit divides the analog signal by 1, 2, 4, or 8, using a resistor network and IC switch. The scaler is controlled by the sound chip through the scale factor signals SF0-SF3. The scaler adds more dynamic range to the digital value; the result is similar to a floating-point value with a sign bit, 11-bit mantissa, and two-bit exponent.4

The scaler divides the voltage by 1, 2, 4, or 8. Based on the DX7 schematics.

Next, the signal goes to a sample-and-hold circuit that samples the analog voltage at a point in time and holds it in a capacitor, kind of like an analog memory. An op-amp buffers the capacitor's voltage so it can be "read" without draining the capacitor. There are two hold circuits, used in alternation, so the last two samples are stored and summed to form the circuit's output.5 The SH1 and SH2 control signals load the analog value into a capacitor, using IC52 as a switch. Finally, the output from the sample-and-hold circuit is filtered,6 the volume is adjusted,7 and the signal is amplified for the output (circuitry not shown).

The sample-and-hold circuit. IC52 looks complicated because it uses pairs of switches in parallel. Based on the DX7 schematics.

To summarize, the sound chip interacts with the output circuitry in three ways. The 12-bit digital value (DA1-DA12) is most important as it specifies the output value for each voice. The scale factor signals (SF0-SF3) are also a key contributor to the signal. The sound chip also provides the sample-and-hold control signals (SH1 and SH2).

Time-division multiplexing

The DX7 has 16 voices, so it can play 16 notes at once. Each note is produced by an "algorithm" that combines 6 oscillators in a particular way, so there are 96 oscillators in total. An oscillator can modulate the frequency of another oscillator to generate complex sounds with FM synthesis.

The chip performs all its processing sequentially, one oscillator at a time, rather than computing the notes in parallel. Internally, the chip has one "operator" calculation circuit to combine oscillators. As shown below, the chip starts by processing operator 6 for note 1, then operator 6 for note 2, and so forth through note 16. Then it processes operator 5 for notes 1 through 16. Finally it processes operator 1 for notes 1 through 16, generating the output sound values. It takes a bit over 20 µs to compute all 16 notes in a complete processing cycle.

Timing diagram of sound production. This time interval corresponds to 49.096 kHz. From the DX7/9 Service Manual.

You might expect the chip to combine the 16 notes into a single digital output. However, the sound chip outputs the 16 notes sequentially, using a technique called time-division multiplexing. Each time interval (~20µs) is divided into 16 intervals and one note is output from the chip per interval. (Note that these intervals don't line up with the intervals in the diagram above.) Thus, digital values are output at 786 kilohertz, 16 times the underlying frequency, and the DAC chip converts them to analog at this rate.

As an example, consider two notes that are sine waves with different frequencies. The digital output would look like the image below. You might think that this signal is unusable since it jumps around wildly from point to point.

Output data with two multiplexed sine waves. (Theoretical, not actual DX7 data.)

However, applying a low-pass filter smooths out the waveform (essentially summing nearby points). The result is the waveform below, which shows the sum of the two sine waves.8 The point is that time-division multiplexing data may look strange, but the analog circuitry's filtering creates a "normal" waveform.

Output data after filtering with a 16 kHz low-pass filter.

Output buffer

Inside the chip, the output buffer stores values for the 16 notes as they are generated, and outputs them in sequence. Rather than RAM, the chip uses shift registers for storage. The shift registers are arranged in a loop of 16 stages, one stage for each note. On each clock cycle, the values in the shift register move to the next stage. The output value is fed back into the shift register's input so the value is retained. Alternatively, a new value can be stored in the shift register. Shift registers provided an efficient way to store data, but they cannot be accessed arbitrarily; instead, data must be processed as it becomes available.

The schematic below shows how one stage of the shift register is implemented. The chip uses a two-phase clock. In the first phase, clock ϕ1 goes high, turning on the first transistor. The input signal goes through the inverter, through the transistor, and the voltage is stored in the capacitor (kind of like DRAM). In the second phase, clock ϕ2 goes high, turning on the second transistor. The value stored in the capacitor goes through the second inverter, through the second transistor, and to the output, where it enters the next shift register stage.

Schematic of one stage of the shift register.

The die photo below shows the output buffer, with the 16 shift-register loops arranged in columns. These hold the 16-bit sound values (four scale factor bits and 16 data bits.) Each shift register is 16 stages long to hold the 16 notes. In the next sections, I'll discuss the bit shifters, the logic, and the output latches.

Closeup of the die, showing the output buffer circuitry.

The scale factor: pseudo floating point

The DX7 uses a 12-bit digital-to-analog converter chip, but the scaling circuit (discussed earlier) will scale the voltage by 1, 2, 4, or 8, which adds more resolution. This isn't quite equivalent to 14-bit resolution; it's more like a floating-point number with a sign, 11-bit mantissa, and 2-bit exponent. This provides more resolution for low signals and reduces signal noise.

Inside the chip, scaling is implemented with a shifter that shifts the data bits by 0 to 3 bit positions. (This is unrelated to the shift registers that hold data.) The shifter (below) is implemented as eleven chevron-shaped logic gates; each gate selects one of four potential bits for each mantissa position.

A data sample is shifted 0 to 4 bits by this shifter circuit.

The operator circuitry generates data as 15 bits (2's complement, so one of the bits provides the sign). The output from the chip is 12 bits, so three bits must be discarded. Normally these are the low-order bits, but by using the shifter, high-order zero bits can be discarded instead, and the external scaler counteracts this. The result is more bits of precision in the output.

The shifter is controlled by the logic circuitry to the left of the buffer, which controls the amount of shift based on the number of leading zeros. (For a negative number, leading 1's.) With 5 leading zeros, the number is shifted left by 3 positions. With 4 leading zeros, the number is shifted by 2 positions. With 3 leading zeros, the number is shifted by 1 position. With 2 or fewer leading zeros, the number is unshifted.

Note that the circuit leaves two leading zeros when it shifts, so it's "wasting" two potential bits of precision. I assume this is because the scaler won't be perfectly linear (due to the resistor imperfections9), so you want to avoid switching scale levels for large signals (which don't really need the extra bits).10

The output latches

As mentioned earlier, the 16 notes are output individually, spaced across the interval. This timing doesn't line up with the timing of the output buffer, which shifts to a new note every clock cycle. To fix the timing, two 16-bit latches sit between the output buffer and the output pins. While one latch outputs the current note, the other latch grabs the next note as it is shifted out of the shift register. At the appropriate time, the latches swap roles; the second latch outputs the note while the first latch waits for the next note.

The timing for the latches is fairly tricky to make sure the note data is loaded into the right latch at the right time. These latches are controlled by the chip's master counter, which is the subject of the next section.

To summarize, the sound chip runs at 4.7 MHz. Data values are produced at this rate (but intermittently) and stored into the output buffer. The output latches provide data values to the DAC chip at 786 kHz for an overall audio rate of 49096 Hertz.

Keeping track of 96 clock cycles: the chip's counter and timing PLA

One complete cycle of the sound chip takes 96 clock cycles: processing all 16 notes through the 6 operators that form an algorithm. Because data can only be accessed when it exits a shift register, everything must be timed so the right data is available at the right time. A critical part of the chip is the counter that keeps track of the current note number and operator number to keep everything synchronized.

On the right of the die photo below is the counter, consisting of seven toggle flip flops: four to count the note number (0-15) and three to count the algorithm number (0-5). On the left is the PLA that defines what happens for particular time slices. (A Programmable Logic Array (PLA) is similar to a ROM, but implements arbitrary logic.) The PLA has 39 columns, each one implementing an AND gate triggered by a particular counter output, corresponding to a particular operator and note. Below the PLA is some logic; mostly buffers with a few gates.

The chip's main counter, along with the control PLA.

Of the PLA's 39 columns, the 32 columns on the left control the data output latches,11 two columns control loading data values into the output buffer, one generates the chip's sync output signal, three reset the operator count, and the last increments the operator count.12

Sample-and-hold

The chip outputs two signals to control the sample-and-hold circuitry, SH1 and SH2. These signals are activated in alternation to take an analog sample of each digital output.

The sound chip on the DX7 schematic has three missing pins, indicated in red.

The sound chip has three unused pins next to the SH1 and SH2 pins; the DX7 schematic doesn't show pins 6-8. I traced the chip's internal circuitry and found that these pins, in conjunction with the sample-and-hold pins, count out the 16 samples. It appears that the chip is designed to sample-and-hold all 16 notes individually, so the synthesizer could have had separate outputs for all 16 notes.13

Moreover, the chip has data buffers to hold separate algorithm algorithms for the 16 notes. This would let the chip drive 16 independent voices, each with a separate algorithm. My conclusion is that the sound chip supports much more flexibility than is used in the DX7 synthesizer.

Conclusion

The DX7 generates sounds digitally and then converts the digital values to the analog output. This process turns out to be more complicated than one would expect, with circuitry inside the chip interacting with synthesizer circuitry to scale and adjust the signal. My hope is that my analysis of this process will help DX7 emulators to achieve more accuracy. Looking at the chip's internal circuitry reveals the floating-point format of the output data as well as the function of the three unused pins.

I plan to continue investigating the DX7's circuitry, so follow me on Twitter @kenshirriff for updates. I also have an RSS feed. Thanks to Jacques Mattheij and Anthony Richardson for providing the chip and discussion.14

Notes and references

1. My previous posts on the DX7: DX7 reverse-engineering, The exponential ROM, The log-sine ROM, and How algorithms are implemented. ↩

2. The DAC chip is the BA9221, a 12-bit D/A converter that produces an output current based on a 2's-complement input value. A datasheet is here. The DAC receives an input voltage reference. This voltage reference can be one of 8 values selected by a multiplexer. This allows the overall volume to be set via MIDI, but only with 3-bit resolution (see the DX7 ROM code here). The volume is an exponential function (so linear in decibels) except that 0 is off. Also see this DAC discussion and this StackExchange discussion.) ↩

3. The output from the DAC is centered around 7.5 volts. In other words. a digital value 0 corresponds to 7.5 volts, with positive digital value above 7.5 volts and negative digital values below 7.5 volts. I would have expected the signals to be centered around 0 volts, which is what the DAC datasheet shows. I think strictly positive voltages were used because they work better with the TC4066 and TC4066 integrated circuits switches (IC 41 for scaling and IC 52 for sample-and-hold respectively). The DX7 converts the signals to zero-centered voltages for the low-pass filter. ↩

4. The amplitude scaler is built from an R-2R resistor ladder, similar to a DAC circuit. However, the attenuator only has 4 useful values, not the 16 levels you might expect with four control lines, because only one control line can be activated at a time. Combinations of control lines do not yield useful outputs. For example, if the top switch is on, you get the maximum output regardless of the other switches. Other switch combinations are non-monotonic. Thus, the scaler only provides two additional bits of resolution, not four. ↩

5. The benefit of keeping two samples is not clear to me. One theory is that this reduces intermodulation distortion between the voices, the effect of one signal on another. With one "solid" sample and one changing sample, the effect of the changing sample will be reduced. Another, more speculative, possibility is that the circuitry was originally designed for stereo, holding one sample for each channel. ↩

6. The filter is a sharp low-pass filter around 16 kHz using a Sallen-Key topology. ↩

7. The volume is controlled by an external volume pedal and a volume control on the synthesizer. The signal also passes through a relay, which cuts the output when the synthesizer is being reset (presumably to avoid random noise).

   The external volume pedal has an interesting circuit. The pedal is essentially a variable resistor, so you might expect the output signal to pass through it. Instead, the pedal is connected to a photocoupler with an LED and a cadmium sulfide photocell inside. The output signal passes through the photocell and is attenuated as controlled by the LED. I think the motivation behind using a cadmium sulfide photocell instead of a phototransistor is that the photocell is completely resistive, so there is no nonlinear distortion of the signal. ↩

8. Time-division multiplexing and filtering isn't perfect, and will contribute some artifacts to the output. In particular, there will be some aliasing, where high frequencies turn into lower frequencies. The low-pass filter will eliminate most of the high frequencies—I believe the DX7's filter is at 16 kHz—but it's not perfect and will add its own color to the sound. Two notes could also interact differently based on their relative positions in the time slice. These artifacts probably contribute to the DX7's characteristic sound. You could consider the artifacts desirable if you're trying to duplicate the DX7 sound. ↩

9. The scale resistors are marked on the schematic with Ⓑ, which probably indicates they are higher-precision resistors. Assuming they are 1% resistors, a 1% error in a large signal would be much more error than the benefit of additional bits of precision. For smaller signals, the additional bits reduce the quantization noise, which is probably more important than the nonlinearity error from scaling. ↩

10. There's an interesting timing issue for the scale calculation. The scaling logic requires about 3 clock cycles to determine the scale factor, so the straightforward implementation would shift a voice based on the amplitude of an earlier voice. The solution is that the 5 bits for scale calculation are pulled out of the operator shift register six stages (3 clock cycles) earlier. Thus, these shift registers have two output; the "early" output gives the scale factor circuitry time to work. ↩

11. The output buffer has two latches, used by alternating notes. Each latch has one control line to latch a data value and one control line to output the latched value, so there are four control lines in total. Curiously, it appears that the notes aren't output sequentially; the order is 1, 13, 5, 11, 3, 15, 7, 10, 2, 14, 6, 12, 4, 16, 8, 9. I don't know if there's a motivation for this; it's also possible that I'm misinterpreting the circuit. ↩

12. A few notes on the PLA outputs in case anyone looks at them more closely. Because signals get delayed through multiple shift registers and clock cycles, things don't happen on the cycle you'd expect. For instance, SYNC is generated 6 cycles before the end. Likewise, loading of the output buffer is triggered midway through operator 6, about 26 cycles later than operator 1 started generating outputs. Most PLA columns are triggered for a specific voice and operator value. The exception is the last column, which increments the operator regardless of the operator value. Curiously, there are three counter reset lines. One resets near the end of operator 1 (as you'd expect). The other two reset near the end of the two invalid operator values (there are 6 operators but 8 possible bit values). Presumably this keeps the synth from starting up in a bad state. Below the PLA are some gates. These are mostly buffering and clock synchronization. ↩

13. Someone with a DX7 could probe the three unused pins and verify that they count out the notes. ↩

14. For more information on the DX7 internals, see DX7 Technical Analysis, DX7 Hardware, OPLx decapsulated, and the video Emulating the DX7 the hard way. ↩

Simulating the IBM 360/50 mainframe from its microcode

The IBM System/360 was a groundbreaking family of mainframe computers announced on April 7, 1964. System/360 was an extremely risky "bet-the-company" project for IBM, costing over $5 billion, but the System/360 ended up as a huge success, setting the direction of the computer industry for decades. The S/360 architecture was so successful that it is still supported by IBM's latest mainframes, almost 60 years later. I'm developing a microcode-level simulator1 for the IBM System/360 Model 50 (link to the simulator); this blog post provides background to understand the Model 50 and the simulator.

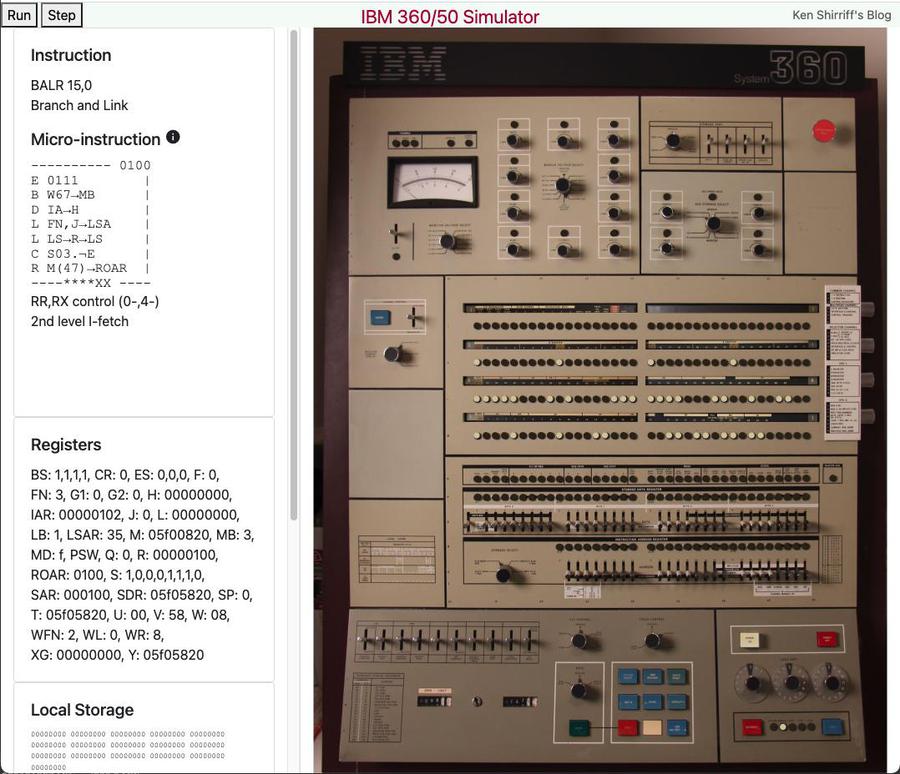
Screenshot of the simulator running in a browser.

The radical decision behind System/360 was to use a single architecture for the entire product line of computers.3 The name symbolized “360 degrees to cover the entire circle of possible uses.” Using a common architecture seems obvious now (e.g. x86), but prior to the System/360, IBM (like other computer manufacturers) produced multiple computers with entirely incompatible architectures.

Internally, the different System/360 models had completely different implementations to support a wide range of cost and performance levels: the fastest model was over 1000 times as powerful as the slowest. Low-end models used simple hardware and an 8-bit datapath while advanced models used wide datapaths, fast semiconductor registers, out-of-order instruction execution, and caches.2 Despite these internal differences, the models all looked the same to the programmer.

Architecture of System/3604

You might expect a computer architecture from the 1960s to be simple, but System/360 is remarkably complex, partly because it merged six computer families into one architecture. It is a 32-bit architecture that supports many datatypes. As well as 32-bit integers and half words, it supports decimal arithmetic on numbers up to 31 digits long. Floating-point arithmetic supports short (32 bit), long (64 bit), or extended (128 bit) values. The processor also supports character strings up to 256 bytes long.

The System/360 instruction set has about 100 different instructions and several addressing modes. Some of these instructions are straightforward arithmetic, logic, or control operations. Other instructions are more complex, such as the "character move" that copies up to 256 characters in memory, or the floating-point instructions.

One of the most complex instructions is "edit", which formats a sequence of decimal digits for printing, for example inserting commas, a minus sign, or decimal point; removing leading zeroes, or filling leading spaces with characters. The number 1234567 could be "edited" into the string "$***12,345.67" for printing on a check. Keep in mind that this is a single instruction, not a library function like printf.

IBM System/360 Model 50 control panel. The dataflow diagram in the upper right illustrates the system's internal design. Photo by Sandstein, CC BY-SA 3.0.

The System/360 architecture also included I/O, defining IBM's "channel" architecture. A channel is a programmable I/O subsystem with its own instruction set. On larger systems, the channel was an independent unit connected to the computer. But smaller systems such as the Model 50 used the same microcode engine to run CPU programs and channel programs.

The point is that System/360 has a large and complex instruction set. A single instruction could result in hundreds of memory accesses and processing steps. The dense instruction set helped programmers to cram programs into the extremely limited core memory of the 1960s. However, the complex instruction set was a problem for the computer designer, who had to implement the complex circuitry to carry out these instructions. The solution was microcode.

The System/360 Model 50 in a datacenter. The console and processor are at the left. An IBM 1442 card reader/punch is behind the IBM 1052 printer-keyboard that the operator is using. At the back, another operator is loading a tape onto an IBM 2401 tape drive. Photo from IBM.

Microcode

One of the hardest parts of computer design is creating the control logic that tells each part of the processor how to carry out each instruction. In 1951, Maurice Wilkes came up with the idea of microcode: instead of building the control circuitry from complex logic gates, the control logic could be replaced with code (i. e. microcode) stored in a special memory called a control store. To execute an instruction, the computer internally executes several simpler microinstructions, specified by the microcode. Microcode turns the processor's control logic into a programming task instead of a logic design task.5

Microcode played a key role in the success of the System/360, helping IBM produce a line of computers with the same instruction set architecture but widely different implementations. It also allowed a processor to support different instruction sets; System/360 machines could be backward compatible with customers' older machines6 so customers could keep their existing software. For these reasons, the System/360 computers used microcode unless there was a compelling reason not to.7

Another advantage of microcode is that it provides an easy way to fix design flaws and bugs in the field. Instead of modifying the hardware, a service engineer could replace the microcode with a new version. The photo below shows a copper sheet with microcode etched into it for the Model 50.

A replaceable BCROS sheet, holding 17,600 bits. Photo courtesy of Glenn's Computer Museum.

Microcode can be implemented in a variety of ways. Many computers use "vertical microcode", where a microcode instruction is similar to a machine instruction, just less complicated. The System/360 designs, on the other hand, used "horizontal microcode", with complex, wide instructions of up to 100 bits, depending on the model. These microinstructions were more like a collection of fields, each controlling low-level signals. This improved performance since multiple parts of the processor could be controlled in parallel.

Hardware of the Model 508

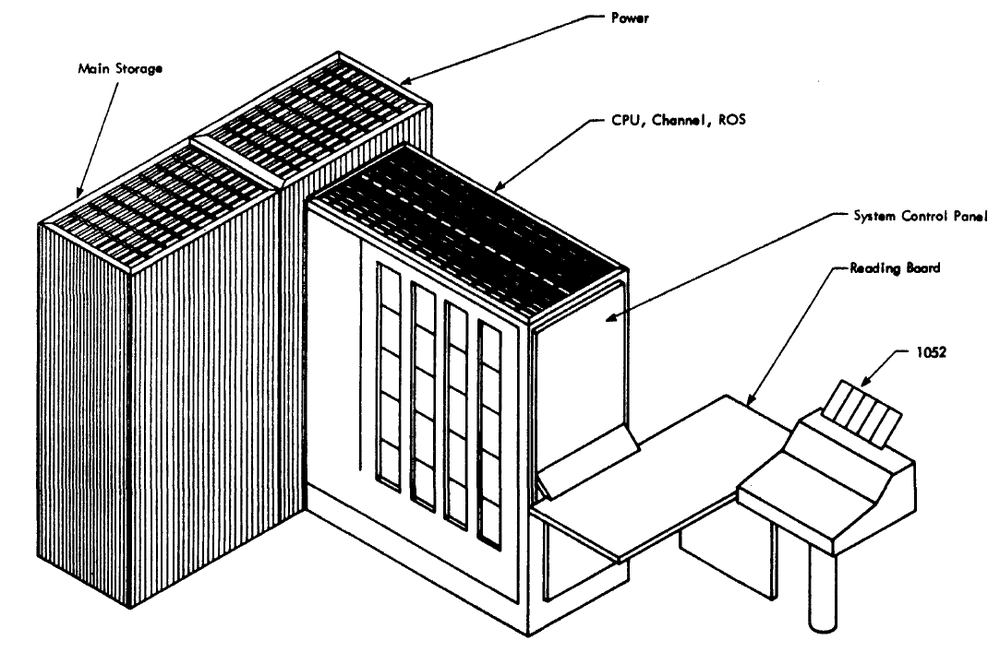
The Model 50 was roughly in the middle of the System/360 lineup, providing a powerful mainframe that could be used by a medium-sized business or university department. The Model 50 typically rented for about $18,000 - $32,000 per month (equivalent to $120,000-$200,000 a month in current dollars).

IBM S/360 Model 50. The console was attached to the main frame, about 5 feet deep. The storage frame and power frame are the black cabinets at the back. Photo from Pinterest.

The Model 50 occupied three large cabinets, each 5 feet long, about 2 feet wide, 6 feet tall, and weighing nearly a ton each.9 The main frame, behind the console, contained the CPU, I/O channel circuitry, and the microcode storage. Behind this, the power cabinet contained the computer's power supplies. To the left, the cabinet at the back contained the main storage: one or two core memory modules, each with 128 kilobytes of memory. (I wrote in detail about the Model 50's core memory earlier.) The computer's cables ran under a raised floor to the I/O devices, which typically included tape drives, a card reader, printers, disk drives, I/O controllers, and so forth.

This diagram shows the three frames that made up the basic S/360 Model 50. Source: Model 50 Maintenance Manual page 138.

The System/360 processors weren't implemented with integrated circuits, but with SLT (Solid Logic Technology) modules, hybrid modules that contain a few transistors, diodes, and resistors. A typical module implemented a logic gate, so it takes many circuit boards full of modules to construct the processor.

A logic board using SLT modules. Each square metal can is a module.

Like most computers of the 1960s, the Model 50 used magnetic core memory, with a tiny ferrite ring to store each bit. The photo below shows a core plane that stores 32768 bits (along with 512 bits for I/O). A stack of 18 planes formed a 64-kilobyte memory module, with two parity bits.10

A Model 50 core plane is arranged as a grid of cores. The Y lines run horizontally. X and sense/inhibit lines run vertically. The sense/inhibit lines form loops at the top and bottom. Each of the four vertical pairs of blocks has separate sense/inhibit lines. Each core plane was about 10¾ × 6¾ × ⅛ inches.

The Model 50's internal architecture

To the programmer, all processors within System/360 look the same; internal circuitry, however, may be entirely different.

It's important to keep in mind that the internal architecture of the Model 50 is very different from the architecture that the programmer sees.11 In particular, the processor's internal registers are invisible to the programmer. The programmer instead sees 16 general-purpose registers and 4 floating-point registers, but to the processor these are part of the 64-word local store, a small high-speed core memory.

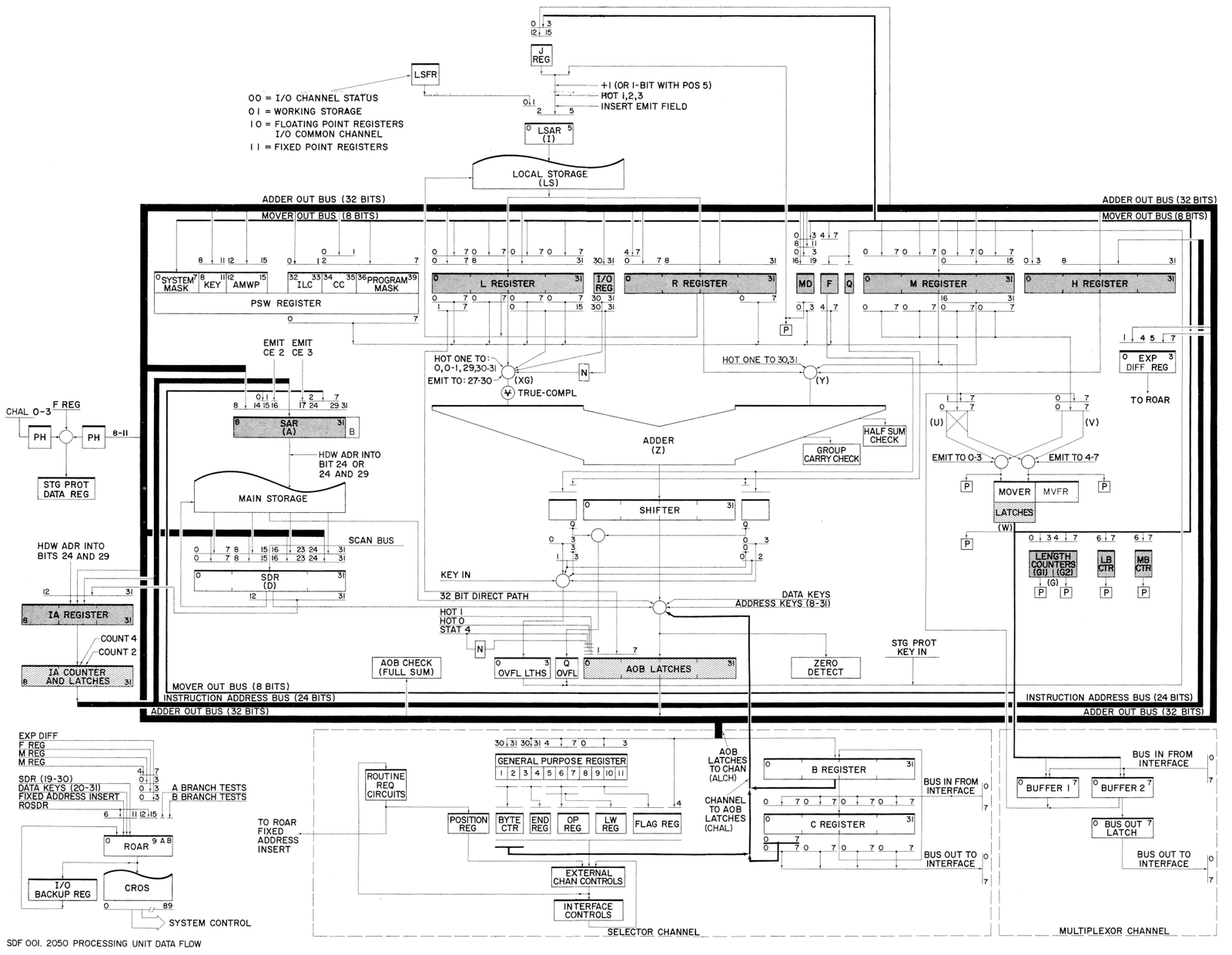
The diagram below shows the complex data flow through the computer.12 The black boxes are internal registers; the processor has a surprisingly large number of registers, used for a variety of purposes. The internal components are connected by buses. Most of the internal communication is over the 32-bit buses, shown in black. The 8-bit "mover" bus is shown in gray.

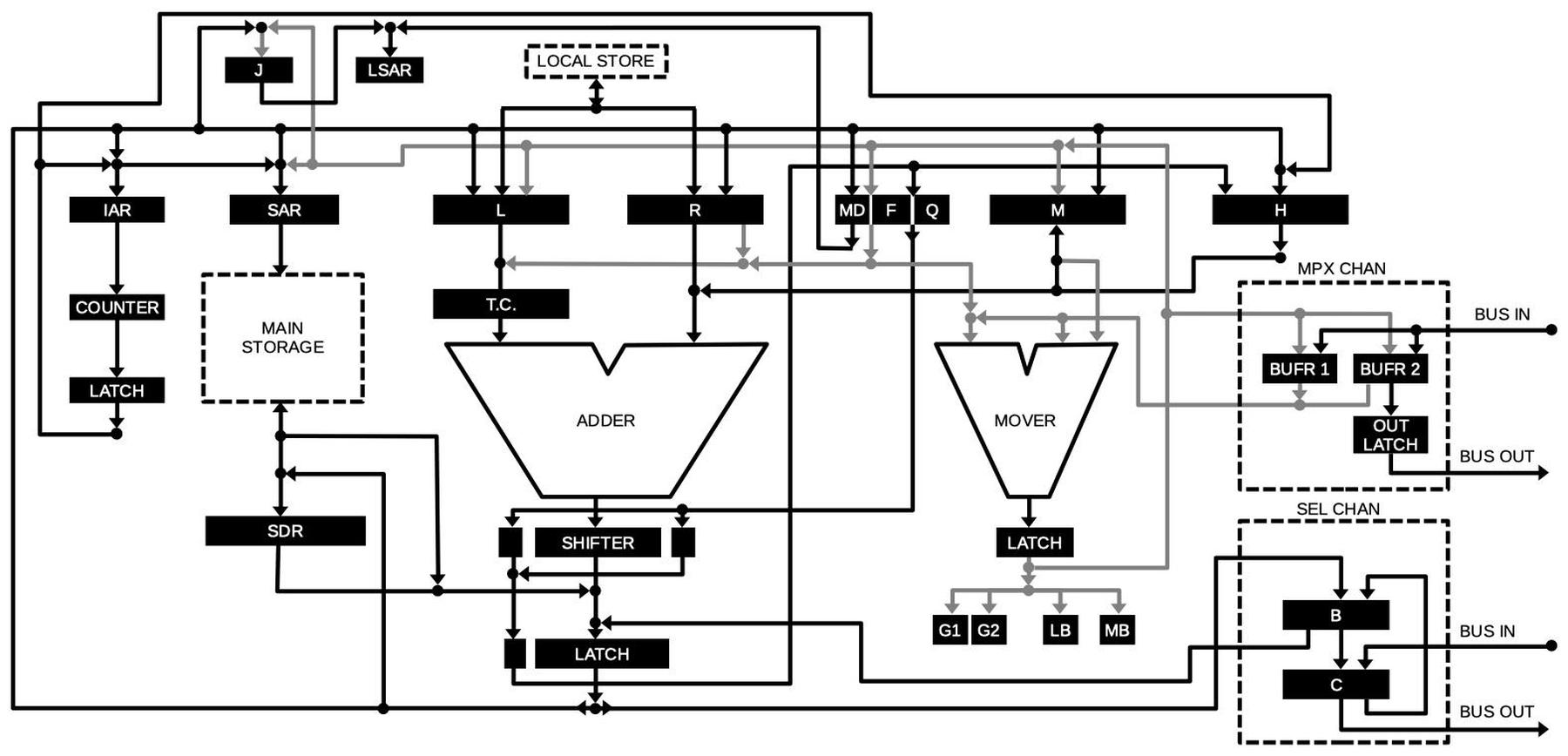
This diagram shows the data flow through the IBM 360/50 and appears in the upper-right corner of the console. I drew this version since I couldn't find a clear photo of it.

The heart of the computer is the 32-bit adder, which performs addition. For subtraction, the argument is complemented by the True/Complement circuit (TC). The adder has an associated shifter to perform bit-shifts; this is especially important for multiplication, division, and floating-point calculations. Operating in parallel with the adder is the "mover", which operates on bytes. It can extract a byte from a 32-bit word, as well as manipulating 4-bit pieces of the byte. The mover also performs Boolean operations (AND, OR, XOR). (Unlike most processors, the Model 50 separates arithmetic and logical operations, instead of having an ALU perform both.)

The computer's main core-memory storage is on the left. To access memory, an address is put in the Storage Address Register (SAR). Data is then read or written through the Storage Data Register (SDR). To the left of main storage, is the Instruction Address Register (the Program Counter or PC in modern terms). At the top is the Local Store, 64 words of high-speed core memory that holds the programmer's registers as well as some internal storage. The local store is accessed through the Local Store Address Register (LSAR).

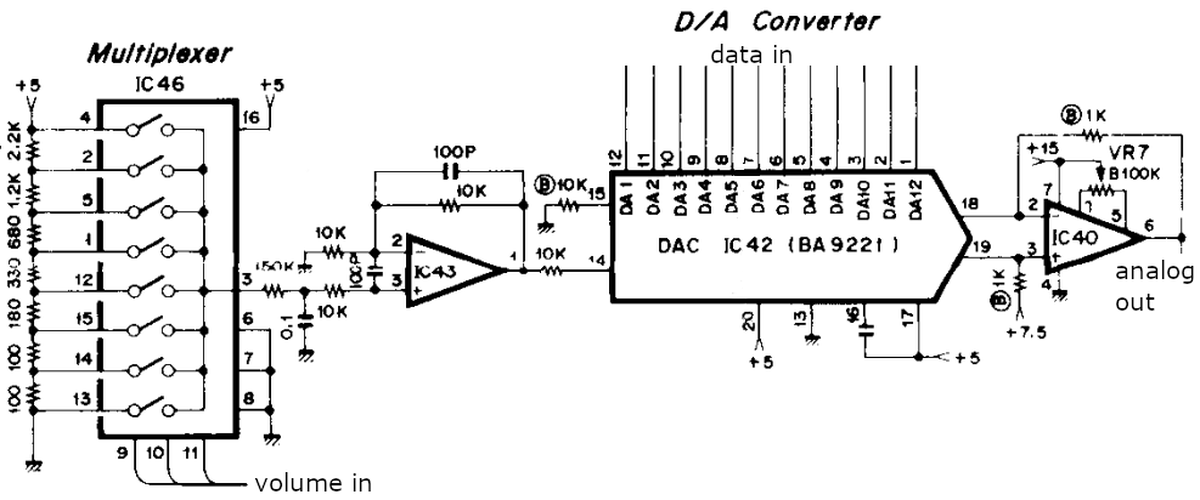
At the right are the I/O channels: the low-speed Multiplexor Channel and the high-speed Selector Channel. You can think of these as DMA (direct memory access) paths for I/O. The multiplexor channel communicates over an 8-bit bus through the mover, while the selector channel communicates over a 32-bit bus. Although the channels are conceptually separate from the processor, the channels use the same buses, circuitry, and microcode engine as the processor. This limits I/O performance compared to more advanced System/360 models that have independent circuitry for the channels.

An example of the microcode

As you can see, the processor has many registers and functional units. The microcode needs to control these components to carry out program instructions. The microcode architecture is very complex and takes over 100 pages to explain thoroughly,15 so I'm only able to scratch the surface here. Each microinstruction is 90 bits long and performs multiple tasks. In the documentation, IBM used an 11-line block to represent each microinstruction, showing all the activities that are taking place in parallel.

A sample microinstruction is shown below, part of the microcode that implements an add instruction. At this point, earlier microinstructions have fetched and decoded the instruction and put the arguments into the R and L registers. This microinstruction performs the actual 32-bit addition, but there's a lot more happening than just the addition.

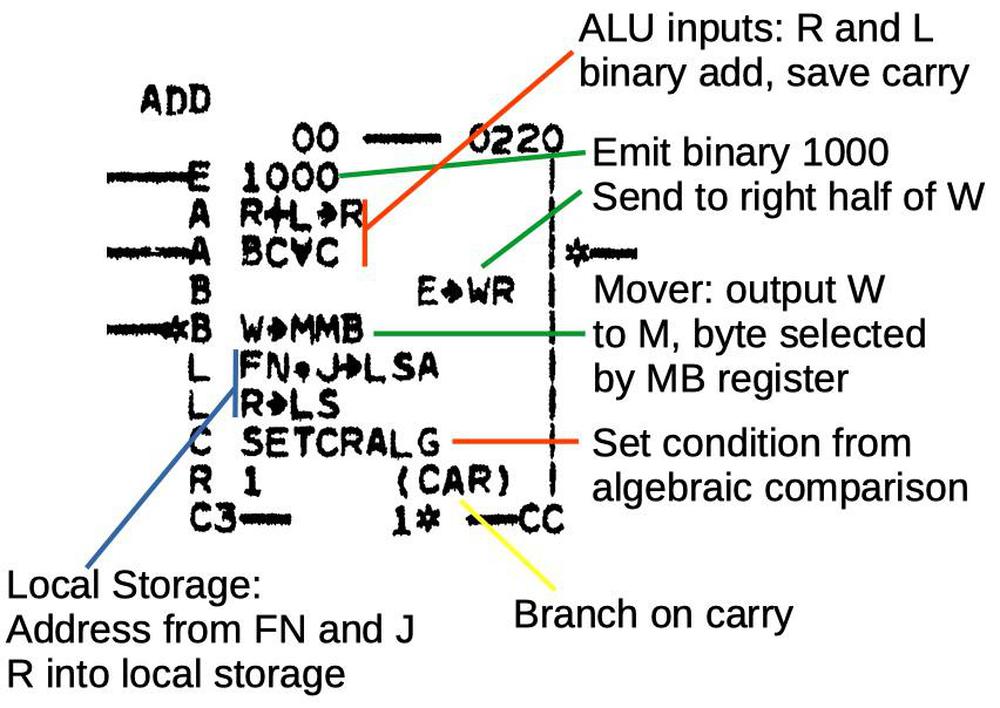
One microinstruction, part of the integer addition code. This microinstruction is at micro-address 0220.

Starting with the line "R+L→R" (red), this indicates that the ALU is taking inputs from registers R and L, and the result is going into the R register. In other words, the two arguments are added. The result R is stored into the desired programmer-visible register in local storage (blue). The processor registers FN and J select the address in local storage. Meanwhile, the SETCRALG line sets the Condition code register based on the sign (i.e. "algebraic" value) of the result, indicating if the result is positive, negative, or zero.

The line "BC⩝C" indicates that signed overflow is detected and used as the carry flag14 while CAR (yellow) indicates the microcode branches on this carry (overflow) value. Thus, the microcode will take one path if the addition was valid and a second error path if overflow occurred. A microinstruction can "emit" an arbitrary 4-bit value (green) which can be used in a variety of ways. In this case, the binary value 1000 is emitted, fed into the W register, and then the M register, for use by the next microinstruction. As you can see, the CPU performs many activities in parallel for one microinstruction, which increases the computer's performance.

All the activities of a microinstruction are encoded into a 90-bit word consisting of 28 fields.13 The microinstruction discussed above (micro-address 0220) is highlighted in the documentation below. A single microinstruction is very complex, which is why it takes an 11-line block of text to represent it.

Part of the microcode listing. The previously-discussed microinstruction is highlighted. Note that the micro-address 0220 matches the address in the upper-left corner of the microinstruction diagram.

The processor documentation contains hundreds of pages of microcode;16 one page of the floating-point multiply code is below. Each box is one microinstruction, and the lines between them indicate the complex control paths. I'm not going to explain this microcode,17 but I wanted to show its complexity.

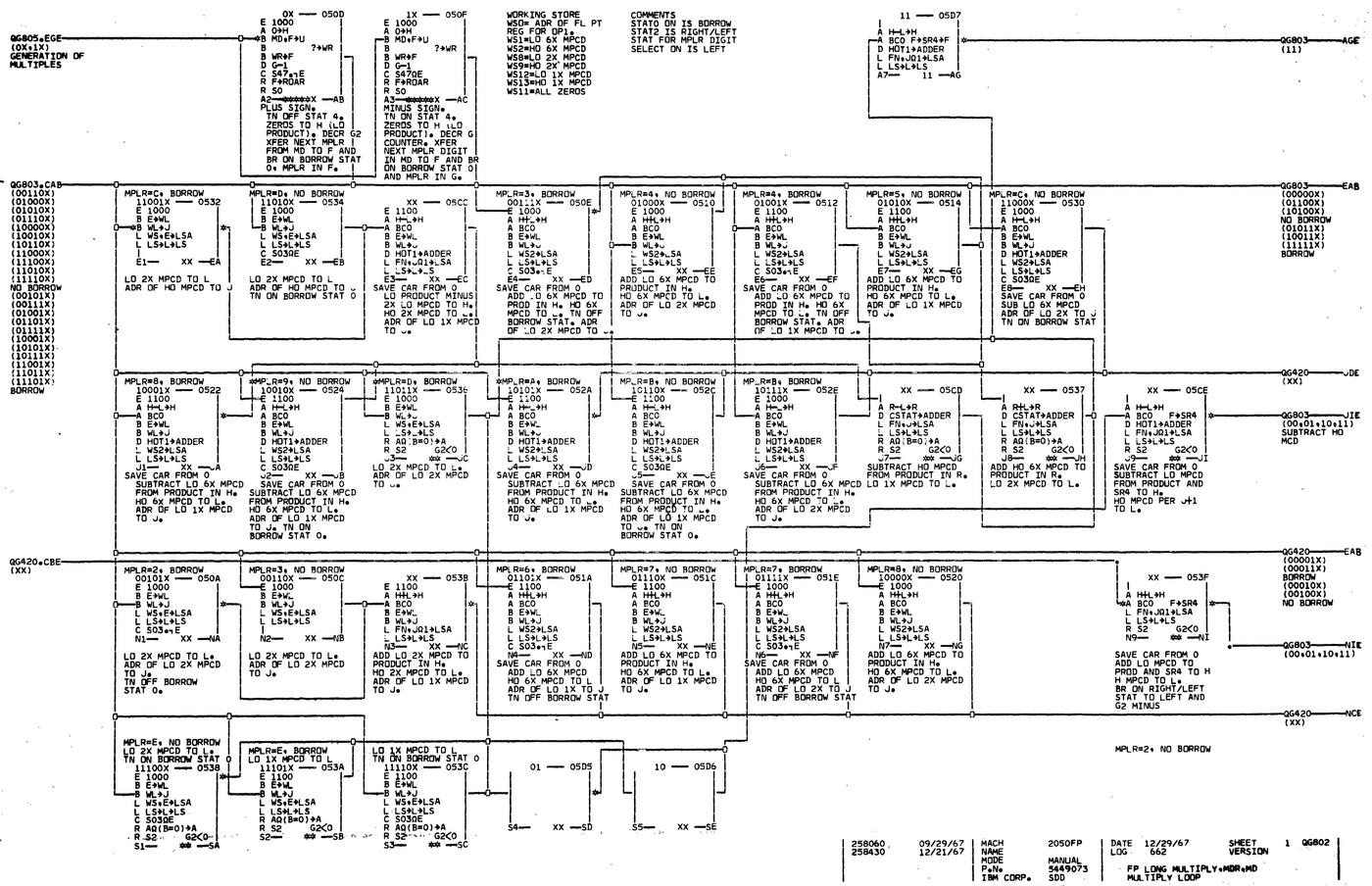
Part of the floating-point multiply microcode. (Click for a larger view.) From ALD vol 18.

The console

The discussion above has shown the complex internal architecture of the Model 50. The numerous lights and controls on the console19 provide a view into this internal state. There were three main uses for the console. The first use was basic "operator control" tasks such as turning the system on, booting it, or powering it off, using the controls in the lower section of the console. These controls were consistent across the S/360 line and were usually the only controls the operator needed. The three hexadecimal dials in the lower right selected the I/O unit that held the boot software. Once the system had booted, the operator generally typed commands into the system rather than using the console.

Control panel of the IBM System/360 Model 50. This panel has marginal check controls for auxiliary storage in the upper right, replacing the dataflow diagram.

The second console function was "operator intervention": program debugging tasks such as examining and modifying memory or registers and setting breakpoints. The lights and toggle switches in the lower half of the console were used for operator intervention. The operator could enter a 24-bit address using the row of 24 toggle switches, and enter a 32-bit data value using the row of 32 toggle switches above. The lights allowed the contents of memory to be examined. With other switches, the operator could set a breakpoint, single-step through a program, and perform other debugging operations.

The third console function was system maintenance and repair performed by an IBM customer engineer. The customer engineering displays took up the top half of the console and provided detailed access to the computer's complex internal state. To save space, the Model 50 had four roller knobs on the right side, with 8 positions for each knob. Each knob position selected a different function for the row of 36 lights (32 bits plus parity). The legends above the lights rotate with the knobs, showing the meaning of each light. For example, one position would display the L register, while another position would display the current microinstruction. In the photo below, the upper roller and lights are displaying part of the microcode currently being executed (ROS = Read Only Store). The roller below shows some of the internal registers and counters.

Closeup of two rollers and the associated lights.

Finally, the voltmeter and voltage control knobs in the upper left of the console were used by an IBM customer engineer for "marginal checking". By raising and lowering the voltage levels, borderline components could be detected and replaced before they caused problems.

The simulator

The simulator is at righto.com/360 and the code is on Github. I implemented the simulator in JavaScript so it can run in a browser. It runs a sample program by executing the Model 50's microcode, simulating each microinstruction and the hardware. Each microinstruction is displayed graphically, along with the current instruction, the registers, the local storage, and core memory. It displays the console lights accurately based on the internal state, on a zoomable virtual console. Each row of lights can display 8 different elements, which you can change by clicking on a roller. You can step also through the microcode, one microinstruction at a time.

This simulator is still under development so don't expect it to work perfectly. I also haven't implemented the toggle switches, so you can't enter a program from the console yet. I also need to implement the I/O system, which has its own registers and a different microcode format.

To build the simulator, I extracted the binary microcode from the listings using a custom OCR tool. I implemented the hundreds of micro-operations, which were tricky to get correct. While most micro-operations are simple operations such as moving a register to the bus, some microinstructions are much more complex, especially for floating-point operations.20 Another complication is that a microinstruction performs many tasks in parallel and it was hard to determine the exact order in which to perform them.

My eventual goal with the simulator is to move it into the physical world. Specifically, I plan to drive the lights on CuriousMarc's Model 50 control panel to make the panel operate accurately. We also plan to hook up his IBM tape drives and card reader so we can have all the pieces of a Model 50 mainframe working together, except for the processor itself. I plan to port the simulator to C so I can run it in a microcontroller to drive the physical console. An FPGA implementation is another possibility; this would provide the maximum speed, but would be harder to implement.

I announce my latest blog posts on Twitter, so follow me @kenshirriff for updates and future articles. I also have an RSS feed. Thanks to Richard Cornwell for discussion and data.

Notes and references

1. My simulator is not particularly useful unless you really care about the microcode in the Model 50. If you want to run software on a simulated System/360, you probably want to use the Hercules system. ↩

2. I'll briefly summarize some of the different implementations used in System/360 computers.

   The low-end Model 30 uses an 8-bit bus and ALU, so 32-bit operations take four steps. It uses 60-bit microcode.

   The Model 40 also has an 8-bit bus and ALU, but it has 16-bit registers and a 16-bit bus to memory, improving the performance. It has 60-bit microcode.

   The Model 50 (discussed in this blog post) has 32-bit registers, memory bus, and adder. It also has the 8-bit mover that can operate in parallel with the adder.

   The Model 65 has a 64-bit bus, and multiple adders (60 and 8-bit) that allow a floating-point fraction and exponent to be processed in parallel. It also has an 8-byte instruction buffer and external channels. It uses 100-bit microcode.

   The Model 75 has a 64-bit main adder, 8-bit exponent adder, 8-bit decimal adder, and a 24-bit addressing adder. It overlaps instruction fetching and execution, with 16 bytes of instruction prefetching and 8 bytes of data prefetching.

   The high-end Model 91 has an advanced superscalar architecture with out-of-order execution, instruction pipelining, and multiple arithmetic execution units. Higher models support memory interleaving for faster access: 2-way on the Model 65 up to 16-way on the Model 195.

   The models 44, 75, 91 and above used hardwired control instead of microcode to squeeze out more performance.

   As you can see, the System/360 line has a wide variety of implementations. At the low end, the hardware is kept to a minimum to reduce costs, while at the high end, more hardware boosts performance, with wider datapaths and multiple functional units providing parallelism. ↩

3. The System/360 line didn't completely meet the goal of a compatible architecture. IBM split out the business and scientific markets on the low-end machines by marketing subsets of the instruction set. The basic instructions were provided in the "standard" instruction set. On top of this, decimal instructions (for business) were in the "commercial" instruction set and floating-point was in the "scientific" instruction set. The "universal" instruction set provided all these instructions plus storage protection (i.e. memory protection between programs). Additionally, cost-cutting on the low-end Model 20 made it incompatible with the S/360 architecture, and the Model 44 was somewhat incompatible to improve performance on scientific applications. ↩

4. IBM defined the System/360 architecture in great detail in a document called the IBM System/360 Principles of Operation. It describes not only the instruction set, but also the datatypes, input/output model, the interrupt model, and even the basic structure of the system control panel. To learn more about System/360, see A Programmer's Introduction to the IBM System/360 Architecture, Instructions, and Assembler Language. A bunch of assembly examples are at rosettacode. ↩

5. The primary benefit of microcode for IBM was economic. As described in Microprogram Control for System/360, the cost of a non-microcoded processor is roughly linear in the size of the instruction set. However, a microcoded system has a roughly fixed cost, with a small overhead for additional instructions. Thus, as instruction sets get more complex (as in System/360), there is a crossover point where microcode is more efficient. This is especially the case for smaller systems where the base cost is lower. The lower marginal cost also makes emulating other systems more feasible. The IBM System/360 was one of the first commercial computers to make extensive use of microcode. ↩

6. Various System/360 machines supported compatibility features with earlier IBM computers including the 1401, 1440, 1620, 7070, 7074, 7080, 709, 7090, 7094. Generally, a smaller System/360 machine could replace a smaller IBM computer such as the 1401, while a larger mainframe such as the 7090 needed to be replaced by a larger System/360 computer such as the Model 65.  ↩

7. A few System/360 models did not use microcode. The Model 44 was designed as a high-performance computer for scientific applications, so it used hardwired control. The Model 85 was partially microcoded, while the Models 75 and 91 were completely hardwired. ↩

8. The book IBM's 360 and Early 370 Systems describes the history of the S/360 in great detail. IBM lists data on each model, including dates, data flow width, cycle time, storage, and microcode size. Another list with model details is here. The article System/360 and Beyond has lots of info. A list of 360 models and brief descriptions is here. For information on the Model 50 specifically, see the Functional Characteristics manual, Field Engineering manuals, Wikipedia, photos here and here, CuriousMarc video. ↩

9. For detailed dimensions of the System/360 components, see the Physical Planning Manual For more memory, another 1500-pound frame could be added to the Model 50, boosting it from 256 kilobytes of memory to 512 kilobytes. Up to four Large Capacity Storage units (IBM 2361) could be added, each providing two more megabytes. ↩

10. I wrote in detail about the Model 50's core memory system here. ↩

11. The quote is from System/360 Model 40 comprehensive introduction. ↩

12. The Model 50 Field Engineering Diagram Manual contains the detailed data flow diagram below. This diagram corresponds to the diagram discussed earlier, but provides much more detail. In particular, it shows the exact bit widths of the various data paths and registers.

    

    The detailed data flow diagram. Click for a larger version.

     ↩

13. The table below shows how a microinstruction is encoded into a 90-bit word.

    Bits	Name	Meaning
    0	P	Parity
    1-3	LU	Mover input left side
    4-5	MV	Mover input right side
    6-11	ZP	ROAR address (Read Only storage Address Register)
    12-15	ZF	ROAR branch control
    16-18	ZN	Address control field
    19-23	TR	Adder control
    24		Unused
    25-27	WS	Local store address control
    28-30	SF	Local store functions
    31	P	Parity
    32-34	IV	Invalid digit test
    35-39	AL	Adder latch gating
    40-43	WM	Mover destination
    44-45	UP	Byte counter function
    46	MD	MD counter control
    47	LB	L byte counter control
    48	MB	M byte counter control
    49-51	DG	Length counter
    52-53	UL	Mover function left digit
    54-55	UR	Mover function right digit
    56	P	Parity
    57-60	CE	Emit field
    61-63	LX	Left adder input
    64	TC	True or complement control
    65-67	RY	Right adder input
    68-71	AD	Adder function control
    72-77	AB	A branch control
    78-82	BB	B branch control
    83		Unused
    84-89	SS	Stat setting control

    For channel instructions, the microcode format is slightly different since some of the fields need to control the channel circuitry. However, most of the fields are the same as for the CPU. The table below shows the microcode format for the channel; the highlighted entries are different from the CPU microcode.

    Bits	Name	Meaning
    0	P	Parity
    1-3	LU	Mover input left side
    4-5	MV	Mover input right side
    6-11	ZP	ROAR address
    12-15	ZF	ROAR branch control
    16-18	ZN	Address control field
    19-23	TR	Adder control
    24		Unused
    25	CS	Local storage address selector
    26-27	SA	Local storage address
    28-30	SF	Local storage function
    31	P	Parity
    32-34	CT	Timing signals to channel
    35-39	AL	Adder latch gating
    40-42	WL	Mover destination
    43-46	HC	Multiplexor channel stat setting
    47-48	CG	Control signals to channel
    49-51	MG	Multiplexor channel gate control
    52-53	UL	Mover function left digit
    54-55	UR	Mover function right digit
    56	P	Parity
    57-60	CE	Emit field
    61-63	LX	Left adder input
    64	TC	True or complement control
    65-67	RY	Right adder input
    68-70	CL	Selector channel adder latch tests
    71		Unused
    72-77	AB	A branch control
    78-82	BB	B branch control
    83		Unused
    84-89	SS	Stat setting control

     ↩

14. When adding twos-complement signed numbers, an overflow occurs if the carry out of the most significant bit is different from the carry out of the second-most-significant bit. (I explain this in detail here.) IBM numbers the bits in a word "backward" with bit 0 the most significant. Thus, an overflow occurs if the carry from bit 0 XOR'd with the carry from bit 1 is nonzero. IBM uses ⩝ to indicate an exclusive or. Thus, CARRY(0) ⩝ CARRY(1) indicates an overflow, represented as BC⩝C in the microcode. ↩

15. For a description of how the Model 50 microcode works, see the book "Microprogramming: Principles and Practices", S. Husson (1970), pages 295 to 411. Bitsavers has a lot of Model 50 documents, but not everything. If you have additional documentation, such as the IBM Automated Logic Diagrams, please let me know. ↩

16. The Model 50's microcode listing is available in three volumes on bitsavers. The binary microcode listings are difficult to read with OCR because pages were printed on different printers; some use serif fonts and others use sans-serif fonts. I made my own OCR program designed to process binary, which was able to read the listings for the most part. The presence of parity in the microcode helped catch errors. ↩

17. Ok, I'll give a brief explanation of that page of microcode, which is part of the implementation of floating-point multiplication. The implementation is designed with tradeoffs between speed, code length, and temporary memory usage. The idea is to multiply the multiplicand by the multiplier, kind of like long multiplication on paper, where you multiply a digit at a time and add the partial sums. This code processes a hex digit of the multiplier at a time, with a separate case for each digit. The multiplicand is multiplied by the digit and this is added to the running total, shifting as appropriate. To make this fast, multiples of the multiplicand are pre-computed. However, pre-computing 16 multiples (one for each hex digit value) would take too much temporary (local) storage. So the only pre-computed multiples are 1, 2, and 6, and these are combined for other digits. To multiply by the digit 7, for instance, the multiples for 1 and 6 are added. To multiply by the digit 4, the multiple for 6 is added and the multiple for 2 is subtracted.

    But what about multiplying by 9 through 15? The trick is to "borrow" 16 from the next-higher digit. For instance, to multiply by the digit 11, you borrow 16, subtract the multiple for 6, and add the multiple for 1. Then the value one less is used for the next digit to account for the borrow. Thus, all 16 possibilities can be handled by adding or subtracting at most two of the pre-computed values. With borrowing, the code needs to handle 32 cases; the included page implements 22 of these cases. This implementation makes multiplication rapid, but the microcode is complex with many paths. (There is also a bunch more code to handle the floating-point exponent, normalizing values, overflow, underflow, and so forth.) ↩

18. Different System/360 models used a variety of methods to store microcode.18 An important feature of IBM's microcode storage was that the microcode could be replaced in the field. The low-end Model 25 held microcode in a 16-kilobyte section of core memory called Control Storage. The Model 30 used CCROS (Card Capacitor Read-only Store), storing the microcode on special metalized punch cards that were read capacitively. Transformer Read-Only Storage (TROS, below) was used by the System/360 Model 20 and Model 40. I wrote an article about microcode storage if you want more information.

    

    A TROS module from an IBM System/360 Model 20.

    The Model 50 (as well as 65 and 67) stored microcode in BCROS (Balanced Capacitor Read-Only Storage), using copper-clad epoxy glass laminate boards, each 20″×8½″. Each sheet plane held 176 words of 100 bits, and the Model 50 used 16 sheets to store 2816 words. (Only 90 of the 100 bits in each word were used.) The data in BCROS was etched into the copper wiring (below). Each bit is represented by two squares: one connected to the upper wire and one connected to the lower wire (or vice versa), forming the balanced capacitors.

    

    Closeup of a BCROS sheet from a System/360 Model 50.

     ↩

19. The features of the system control panel were carefully defined in the System/360 Principles of Operation pages 117-121, providing a consistent operator experience across the S/360 line. (The customer engineering part of the panel, on the other hand, was not specified and wildly different across the product line.) Diagrams of S/360 consoles are at quadibloc. For more details on the consoles, see my article on System/360 consoles. ↩

20. The micro-operation that caused me the most difficulty is ED*FP, which computes the difference between two exponents for floating-point, but also computes four floating-point flags including the sign depending on the type of operation. Not only is this operation complex, but I think there is a typo in the description.

    

    A description of the ED*FP micro-operation.

    Another complex micro-operation is MLJK, which performs multiple actions as part of instruction decoding:

    Gate adder latch to L reg and M reg. Gate latch bits 12-15 to J reg. Gate latch bits 16-19 to MD counter. Turn off refetch stat.
    If latch bits 12-15 all zero, turn on stat 0. Otherwise turn off stat 0.
    If latch bits 16-19 all zero, turn on stat 1. Otherwise turn off stat 1.
    If latch bits 16-17 all zero, turn on one-syllable stat. Otherwise turn off one-syllable stat.
    If latch bits 0-1 equal 00, set ILC to 01.
    If latch bits 0-1 equal 01 or 10, set ILC to 10.
    If latch bits 0-1 equal 11, set ILC to 11. ↩