Silicon die teardown: a look inside an early 555 timer chip

If you've played around with electronic circuits, you probably know the 555 timer integrated circuit,1 said to be the world's best-selling integrated circuit with billions sold. Designed by analog IC wizard Hans Camenzind2, the 555 has been called one of the greatest chips of all time.

An 8-pin 555 timer with a Signetics logo. It doesn't have a 555 label, but instead is labeled "52B 01003" with a 7304 date code, indicating week 4 of 1973. Photo courtesy of Eric Schlaepfer.

Eric Schlaepfer (@TubeTimeUS) recently came across the chip above, with a mysterious part number. He tediously sanded through the epoxy package to reveal the die (below) and determined that the chip is a 555 timer. Signetics released the 555 timer in mid-1972 4 and the chip below has a January 1973 date code (7304), so it must be one of the first 555 timers. Curiously, it is not labeled 555, so perhaps it is a prototype or internal version.3 I took detailed die photos, which I discuss in this blog post.

The 555 timer with the package sanded down to expose the silicon die, the tiny square in the middle.

A brief explanation of the 555 timer

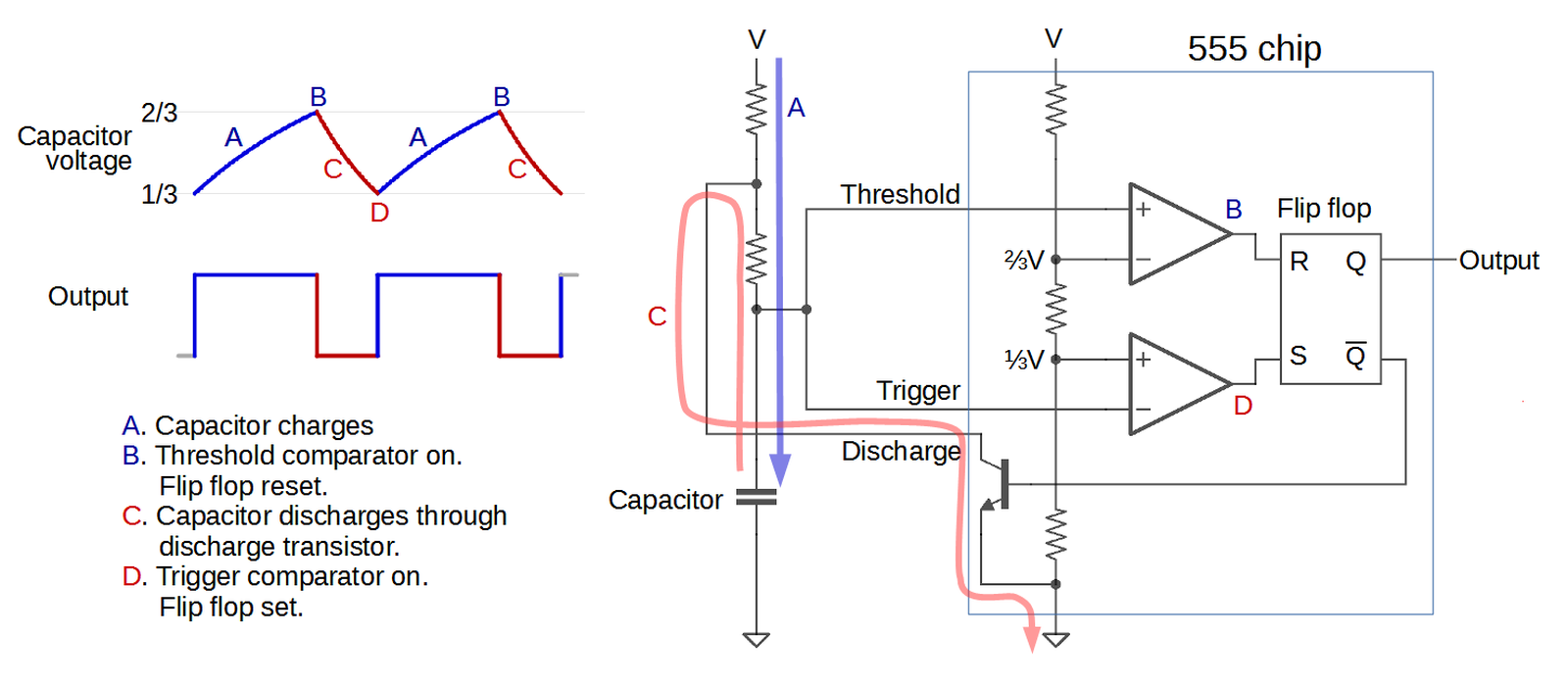
The 555 timer has hundreds of applications, operating as anything from a timer or latch to a voltage-controlled oscillator or modulator. The diagram below illustrates how the 555 timer operates as a simple oscillator. Inside the 555 chip, three resistors form a divider generating references voltages of 1/3 and 2/3 of the supply voltage. The external capacitor will charge and discharge between these limits, producing an oscillation. In more detail, the capacitor will slowly charge (A) through the external resistors until its voltage hits the 2/3 reference. At that point (B), the upper (threshold) comparator switches the flip flop off and the output off. This turns on the discharge transistor, slowly discharging the capacitor (C). When the voltage on the capacitor hits the 1/3 reference (D), the lower (trigger) comparator turns on, setting the flip flop and the output, and the cycle repeats. The values of the resistors and capacitor control the timing, from microseconds to hours.5

Diagram showing how the 555 timer can operate as an oscillator. The external capacitor charges and discharges through the external resistors, under the control of the 555 timer.

To summarize, the key components of the 555 timer are the comparators to detect the upper and lower voltage limits, the three-resistor divider to set these limits, and the flip flop to keep track of whether the circuit is charging or discharging. The 555 timer has two other pins (reset and control voltage) that I haven't covered above; they can be used for more complex circuits.

The structure of the integrated circuit

I created the photo below from a composite of microscope images. On top of the silicon, a thin layer of metal connects different parts of the chip. This metal is clearly visible in the photo as light-colored traces. Under the metal, a thin, glassy silicon dioxide layer provides insulation between the metal and the silicon, except where contact holes in the silicon dioxide allow the metal to connect to the silicon. At the edge of the chip, thin wires connect the metal pads to the chip's external pins.

Die photo of the 555 timer. Click this image (or any other) for a larger version.

The different types of silicon on the chip are harder to see. Regions of the chip are treated (doped) with impurities to change the electrical properties of the silicon. N-type silicon has an excess of electrons (negative), while P-type silicon lacks electrons (positive). In the photo, these regions show up as a slightly different color surrounded by a thin black border. These regions are the building blocks of the chip, forming transistors and resistors.

NPN transistors inside the IC

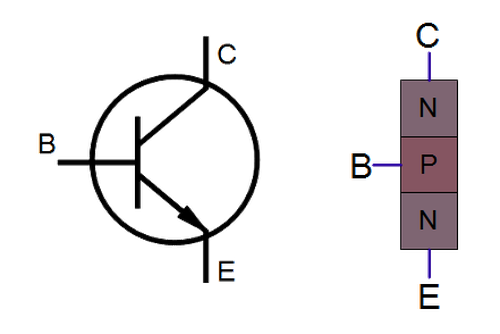
Transistors are the key components in a chip. The 555 timer uses NPN and PNP bipolar transistors. If you've studied electronics, you've probably seen a diagram of an NPN transistor like the one below, showing the collector (C), base (B), and emitter (E) of the transistor, The transistor is illustrated as a sandwich of P silicon in between two symmetric layers of N silicon; the N-P-N layers make an NPN transistor. It turns out that transistors on a chip look nothing like this, and the base often isn't even in the middle!

Schematic symbol for an NPN transistor, along with an oversimplified diagram of its internal structure.

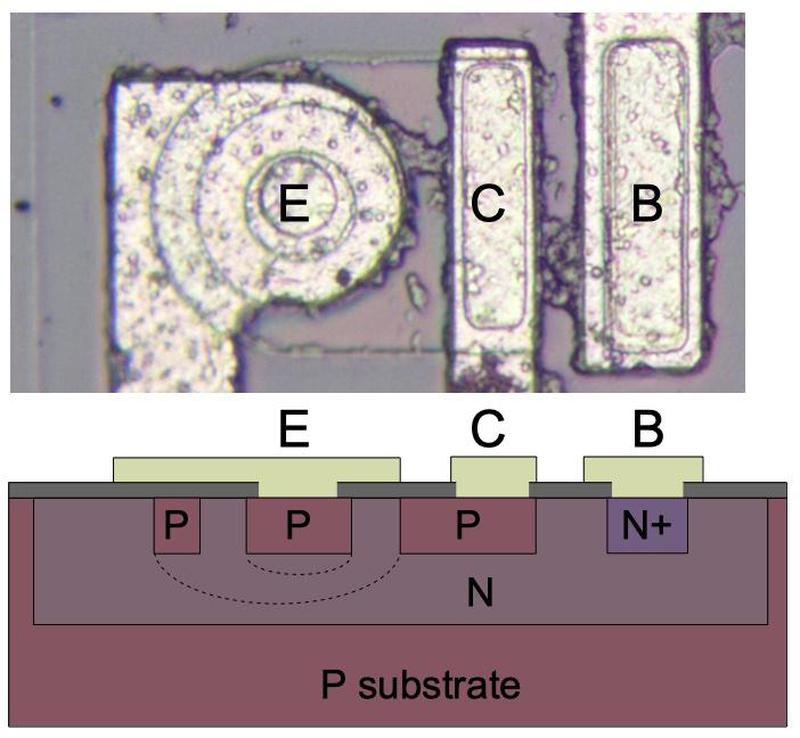
The photo below shows a closeup of one of the transistors in the 555 as it appears on the chip. The slightly different tints in the silicon indicate regions that have been doped to form N and P regions. The whitish areas are the metal layer of the chip on top of the silicon - these form the wires connecting to the collector, emitter, and base.

Structure of an NPN transistor on the die.

Underneath the photo is a cross-section drawing illustrating how the transistor is constructed. There's a lot more than just the N-P-N sandwich you see in books, but if you look carefully at the vertical cross-section below the 'E', you can find the N-P-N that forms the transistor. The emitter (E) wire is connected to N+ silicon. Below that is a P layer connected to the base contact (B). And below that is an N+ layer connected (indirectly) to the collector (C).6 The transistor is surrounded by a P+ ring that isolates it from neighboring components.

PNP transistors inside the IC

You might expect PNP transistors to be similar to NPN transistors, just swapping the roles of N and P silicon. But for a variety of reasons, PNP transistors have an entirely different construction. They consist of a small circular emitter (P), surrounded by a ring-shaped base (N), which is surrounded by the collector (P). This forms a P-N-P sandwich horizontally (laterally), unlike the vertical structure of the NPN transistors.

The diagram below shows one of the PNP transistors in the 555, along with a cross-section showing the silicon structure. Note that although the metal contact for the base is on the edge of the transistor, it is electrically connected through the N and N+ regions to its active ring in between the collector and emitter.

A PNP transistor in the 555 timer chip. Connections for the collector (C), emitter (E) and base (B) are labeled, along with N and P doped silicon. The base forms a ring around the emitter, and the collector forms a ring around the base.

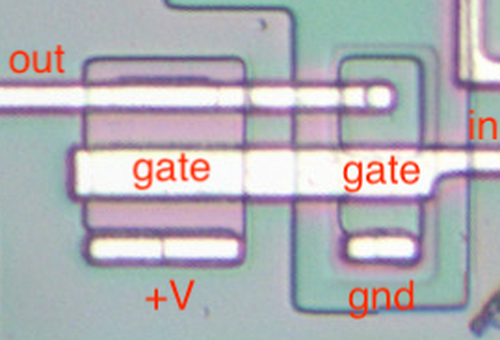
The output transistors in the 555 are much larger than the other transistors and have a different structure in order to produce the high-current output. The photo below shows one of the output transistors. Note the multiple interlocking "fingers" of the emitter and base, surrounded by the large collector.

A large, high-current NPN output transistor in the 555 timer chip. The collector (C), base (B) and emitter (E) are labeled.

How resistors are implemented in silicon

Resistors are a key component of analog chips. Unfortunately, resistors in ICs are large and inaccurate; the resistances can vary by 50% from chip to chip. Thus, analog ICs are designed so only the ratio of resistors matters, not the absolute values, since the ratios remain nearly constant.

A resistor inside the 555 timer. The resistor is a strip of P silicon between two metal contacts.

The photo above shows a 10KΩ resistor in the 555, formed from a strip of P silicon (pinkish gray), contacting metal wiring at either end. Other metal wires cross the resistor. The resistor has a spiral shape to fit its length in the available space. The resistor below is a 100KΩ pinch resistor. A layer of N silicon on top of the pinch resistor makes the conductive region much thinner (i.e. pinches it), forming a much higher but less accurate resistance.

A pinch resistor inside the 555 timer. The resistor is a strip of P silicon between two metal contacts. An N layer on top pinches the resistor and increases the resistance. This resistor is crossed by a vertical metal line.

IC component: The current mirror

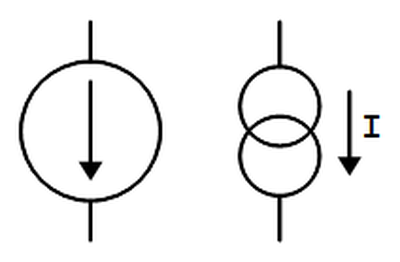
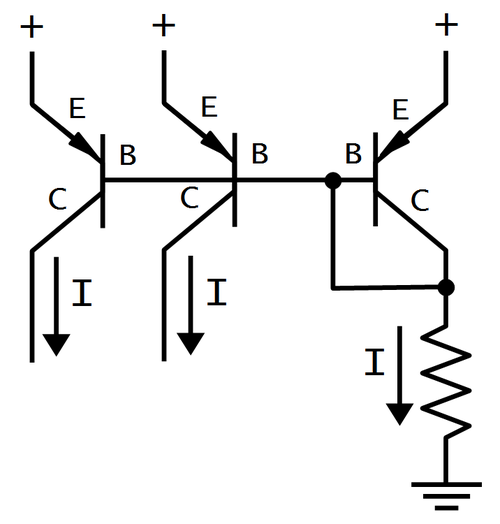
There are some subcircuits that are very common in analog ICs, but may seem mysterious at first. The current mirror is one of these. If you've looked at analog IC block diagrams, you may have seen the symbols below, indicating a current source, and wondered what a current source is and why you'd use one. The idea is you start with one known current and then you can "clone" multiple copies of the current with a simple transistor circuit, the current mirror.

Schematic symbols for a current source.

The following circuit shows how a current mirror is implemented with two identical transistors.7 A reference current passes through the transistor on the right. (In this case, the current is set by the resistor.) Since both transistors have the same emitter voltage and base voltage, they source the same current, so the current on the right matches the reference current on the left.8

Current mirror circuit. The current on the right copies the current on the left.

A common use of a current mirror is to replace resistors. As explained earlier, resistors inside ICs are both inconveniently large and inaccurate. It saves space to use a current mirror instead of a resistor whenever possible. Also, the currents produced by a current mirror are nearly identical, unlike the currents produced by two resistors.

Three transistors form a current mirror in the 555 timer chip. They all share the same base and two transistors share emitters.

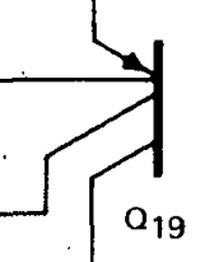
The three transistors above form a current mirror with two outputs. Note the three transistors share the base connection, tied to the collector on the right, and the emitters on the right are tied together. On the schematic, the two transistors on the right are drawn as a single two-collector transistor, Q19.

IC component: The differential pair

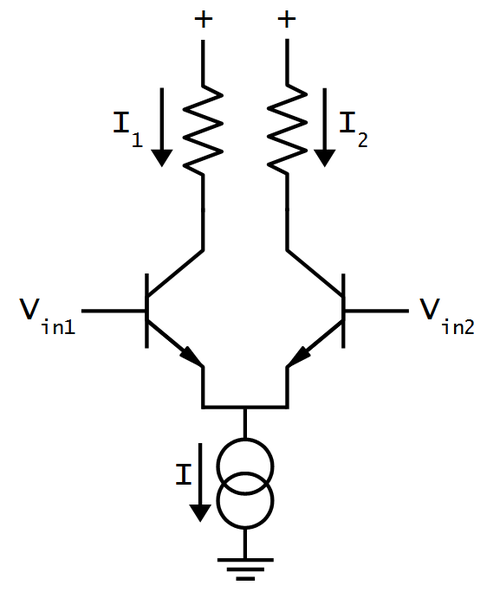
The second important circuit to understand is the differential pair, the most common two-transistor subcircuit used in analog ICs. 9 You may have wondered how a comparator compares two voltages, or an op amp subtracts two voltages. This is the job of the differential pair.

Schematic of a simple differential pair circuit. The current source sends a fixed current I through the differential pair. If the two inputs are equal, the current is split equally.

The schematic above shows a simple differential pair. The current source at the bottom provides a fixed current I, which is split between the two input transistors. If the input voltages are equal, the current will be split equally into the two branches (I1 and I2). If one of the input voltages is a bit higher than the other, the corresponding transistor will conduct exponentially more current, so one branch gets more current and the other branch gets less. A small input difference is enough to direct most of the current into the "winning" branch, flipping the comparator on or off. The 555 chip uses one differential pair for the threshold comparator and another for the trigger comparator.10

The 555 schematic interactive explorer

The 555 die photo and schematic11 below are interactive. Click on a component in the die or schematic, and a brief explanation of the component will be displayed. (For a thorough discussion of how the 555 timer works, see 555 Principles of Operation.)

For a quick overview, the large output transistors and discharge transistor are the most obvious features on the die. The threshold comparator consists of Q1 through Q8. The trigger comparator consists of Q10 through Q13, along with current mirror Q9. Q16 and Q17 form the flip flop. The three 5KΩ resistors forming the voltage divider are in the middle of the chip.12 Urban legend says that the 555 is named after these three 5K resistors, but according to its designer 555 is just an arbitrary number in the 500 chip series.

Click the die or schematic for details...

Conclusion

I hope you've found this look inside the 555 timer chip interesting. Next time you're building a 555 project, you'll know exactly what's inside the chip. I've written about the 555 timer before; this post is pretty much the same as that one but with a different die. I've also written about a CMOS version. Thanks to Eric Schlaepfer13 for providing the die; see his Twitter thread for background on this chip.

I announce my latest blog posts on Twitter, so follow me @kenshirriff and you won't miss an article! I also have an RSS feed.

Notes and references

1. The 555 timer is iconic enough to appear on mugs, bags, caps and t-shirts. Whole books are devoted to 555 timer circuits. ↩

2. The book Designing Analog Chips written by the 555's inventor Hans Camenzind is really interesting, and I recommend it if you want to know how analog chips work. Chapter 11 has an extensive discussion of the 555's history and operation. Page 11-3 claims the 555 has been the best-selling IC every year, although I don't know if that is still true. The free PDF is here or get the book. ↩

3. The die has the part number 1000 and revision "C", so this probably corresponds to the 01003 number on the package. I suspect this chip is the third mask revision of the original 555.

   

   The first 555 die with the part number "1000" highlighted and the revision "A" magnified.

   The die of the first 555 timer version (above) is marked with the number "1000" and revision "A". I compared this image with the die photo that I took and I couldn't see any differences except the revision changed to "C". The mask changes must have been fairly subtle. (This image is at Wikipedia and IEEE Spectrum. The image is captioned as the die shot of the first 555 timer IC manufactured in 1971.) ↩

4. The 555 chip was introduced in mid-1972 according to Signetics Analog Applications page 149. ↩

5. The brilliant part of the 555 timer is that the oscillation frequency depends only on the external resistors and capacitor and is insensitive to the supply voltage. If the supply voltage drops, the 1/3 and 2/3 references drop too, so you might expect the oscillations to be faster. But the lower voltage charges the capacitor more slowly, canceling this out and keeping the frequency constant.

   This voltage insensitivity is so tricky that the chip's designer didn't figure it out until near the end of the 555's design, but it made a big difference. The original design was more complex and required nine pins, which is a terrible size for an IC since there are no packages between 8 and 14 pins. The final, simpler 555 design worked with 8 pins, making the chip's packaging much cheaper. (See page 11-3 of Designing Analog Chips for the full story.) ↩

6. You might have wondered why there is a distinction between the collector and emitter of a transistor, when the typical diagram of a transistor is symmetrical. As you can see from the die photo, the collector and emitter are very different in a real transistor. In addition to the very large size difference, the silicon doping is different. The result is a transistor will have poor gain if the collector and emitter are swapped. ↩

7. For more information about current mirrors, check wikipedia, any analog IC book, or chapter 3 of Designing Analog Chips. ↩

8. The schematic has the unusual symbol below, which indicates a transistor with two collectors. The base is drawn on the same side as the emitter and collectors, which adds to the confusion. On the die, this transistor is implemented with two separate transistors, with the emitters and the bases wired together. Other circuits sometimes use a single transistor that has two physical collectors present.

   

   This symbol indicates a transistor with two collectors.

    ↩

9. Differential pairs are also called long-tailed pairs. According to Analysis and Design of Analog Integrated Circuits the differential pair is "perhaps the most widely used two-transistor subcircuits in monolithic analog circuits." (p214) For more information about differential pairs, see wikipedia, any analog IC book, or chapter 4 of Designing Analog Chips. ↩

10. In the 555, the threshold comparator uses NPN transistors, while the trigger comparator uses PNP transistors. This allows the threshold comparator to work near the supply voltage and the trigger comparator to work near ground. The 555's comparators also use two transistors on each input (Darlington pair) to buffer the inputs. ↩

11. The 555 schematic used in this article is from the Philips datasheet. It is identical to the Signetics schematic p150. ↩

12. Note that the three resistors for the voltage divider are parallel and next to each other. This helps ensure they have the same resistance even if there are electrical variations across the silicon. ↩

13. Evil Mad Scientist sells a very cool discrete 555 timer kit, duplicating the 555 circuit on a larger scale with individual transistors and resistors — it actually works as a 555 replacement. Their 555 footstool is also worth a look.

    

    Large-size 555 timer created by Evil Mad Scientist Lab.

     ↩

Christmas shopping the IBM way: computerized gift selection in 1962

In 1962, the Simpson's department store in Toronto used an IBM computer to help customers select Christmas gifts, based on the characteristics of the recipients.1 I came across a video that shows how it worked.

"Now! A computer makes Christmas shopping easier." The IBM 1401 computer is the cabinet at the back, with the 1403 printer to the right of it. The 1402 card reader is at the left and the 729 tape drives at the right, (Click for a larger version.) Advertisement in The Financial Post, November 24, 1962.

The IBM 1401 computer (below) was pre-programmed with 3000 categorized gifts.2 A customer described the gift recipient: their age range, their interests, their gender (male, female, or couple), the gift category (e.g. apparel, personal, or "the man who has everything"), and the price range (ranging from $5 to "money is no object").

The IBM 1401 computer at Simpson's department store in 1962. The computer is barely visible behind the man's head. The 1402 card reader is at the left. Still from CBC video.

This information was punched onto a card by an operator (called a "girl" in the interview) using an IBM 26 keypunch, as shown below.

Entering the customer data into the IBM 26 keypunch. Still from CBC video.

After running the card through the computer, a gift list with ten suggestions was printed on the IBM 1403 line printer. The list was torn off and given to the customer to help with their shopping.

Removing the Christmas shopping list from the IBM 1403 line printer. The Simpson's logo is barely visible in the upper left corner. Still from CBC video.

The gift suggestions included a King James bible, Eskimo soapstone, a leather-covered cigarette case, Cossack boots, a Marabou-trim bed jacket, Roto-Shine electric shoe polisher ($26.95), a table lighter in the design of an antique pistol ($4.95), a soda siphon ($15.95) "a little more expensive, probably for your father or your husband", an electrified magnifying glass "to read the stock market report" ($7.95), or moccasins trimmed with seal fur ($6.95). (Gift ideas seem to have changed drastically since the 1960s.)

The interviewer suggested that this computer might take all the fun out of Christmas shopping and called it a "Santa monster", but the operator insisted that most people need some help with their shopping. It must have been an unusual experience for people to encounter a computer in person back then, but this gift computer was very popular, with 2000 people a day using it.

I announce my latest blog posts on Twitter, so follow me @kenshirriff. I also have an RSS feed. Thanks to Tim and Lisa Robinson for tracking down the newspaper clipping.

Notes and references

1. The video is Christmas Shopping the IBM Way, broadcast on CBC on Dec 18, 1962. The host was Anna Cameron with guest Brian Finney. (Only the first part of the video shows the computer system; most of the video discusses the gift choices in detail.) The system was also discussed in a CBC Radio segment, Christmas Computer Selects the Perfect Gift, reported by Jim McLean and Joelle Pearson on Dec 4, 1962. The radio interview also discusses the use of the system at Gimbel's department store in New York. ↩

2. The IBM 1401 computer is just barely visible in the video, so here's a photo that shows an IBM 1401 computer more clearly.

   

   An IBM 1401 computer. The line printer (1403) is in the foreground, while IBM 729 tape drives are in the background. This computer is at the Computer History Museum.

    ↩

Reverse-engineering a tiny 1980s chip that plays Christmas tunes

For the holidays, I decapped a chip that plays three Christmas melodies. The UM66T melody chip from the 1980s was designed for applications such as greeting cards and toys. It looks like a transistor, but when connected to a battery and speaker it plays music. The die photo below shows the tiny silicon chip that I reverse engineer in this blog post.

The UM66T die under the microscope. Click this (or any other) image for a larger version.

The video below shows the chip in action. Click to hear the chip play Jingle Bells, Santa Claus is Coming to Town, and We Wish You a Merry Christmas.

The chip is packaged in a 3-pin package that looks like a transistor (below). I dissolved the epoxy package in boiling sulfuric acid to expose the silicon die inside. This was my first acid decap and it turned out okay, although there are some scratches on the die. The composite photo above shows the CMOS chip under the microscope. The features are fairly large, even for the time; the metal traces are about 3.3µm wide and the silicon about 5.4µm.

The chip is in a 3-pin TO-92 package, like a transistor.

The silicon die is very small, about 1.8mm×1.8mm. The photo below gives an idea of the scale.

The UM66T die on top of a penny.

I've labeled the die photo with the functional blocks. The melody chip is an optimized, minimal design. It is constructed from flip-flops and gates, not the microcontroller you might expect.

Die photo of the UM66T with the main functional blocks labeled.

The chip has 3 pins, but there are 8 pads on the die. The other pins appear to be used for testing. By activating one of the pins, the chip can be put into a test mode. The test mode runs through the songs at 512× speed so the chip can be tested quickly without waiting for the tunes to play. The other test pins appear to expose other internal data for testing.

The block diagram below shows the structure of the chip. (Inconveniently, I didn't get this diagram until after I'd reverse-engineered the circuitry.) The basic idea is that the "program counter" steps through the 64 notes stored in the melody ROM. Four bits form the note pitch index, while two bits select the note duration. The Scale ROM and tone generator are used to convert the pitch index into the desired output tone. Meanwhile, the Rhythm ROM converts the 2-bit note duration into a 4-bit value indicating how long the note is.

Block diagram of the UM66T. From Maplin Magazine, March 1988.

The chip is built from CMOS, like most modern ICs. The photo below shows an inverter: a PMOS transistor on the left and an NMOS transistor on the right. The PMOS one turns on with a 0 input, pulling the output high. The NMOS transistor turns on with a 1, pulling the output low. Thus, the two transistors implement the desired inverter behavior.

Structure of an inverter.

The melody ROM

The 64 notes are stored in a 64×6 ROM, shown below. Each note is 4 bits for the frequency and 2 bits for the duration of the note. The ovals are the transistor gates; bits are stored in the wiring pattern of the transistors, either to the left or to the right. The vertical column select lines from the top select one column in the ROM. The vertical lines from the bottom, however, inactivate the transistor.

Physically, the ROM stores four notes in each column, so it has 16 columns of 24 bits. At the top of the ROM is a binary decoder that energizes one of the 16 columns, based on the input value. The transistors at the left of the ROM select one bit out of each four to produce the desired 6-bit word. The 6 bits are latched. Then 4 bits are used to generate the desired note frequency, while two bits select the duration of the note (half note, quarter note, or eighth note).

The melody ROM holds 64 notes.

In the diagram above, the numbers show the locations of the first four words. The first word is 000100, a start code. The next two words are 011100; 0111 indicates the note E5 and 00 indicates a short duration.1 The next word is by 011101, indicating a longer E5. Thus, the indicated words store the first three notes of "Jingle Bells".

The metal layer of an IC can be changed relatively easily. By changing the metal layer, different versions of the chip could be manufactured with different ROMS, producing different songs. (The chip could also be manufactured with different note ranges, tempo, and beats, providing more flexibility.) The table below shows the songs that were available.2

List of songs available in the UM66T chip line. From the datasheet.

Generating the note frequency

The melody ROM doesn't specify the note's frequency directly, but instead has a value from 0 to 15. A second ROM, the scale ROM, has the mapping to convert the note value into a frequency. Specifically, the output frequency is 32768÷N, where N is the value in the scale ROM. The frequency resolution from this isn't great, so some notes are noticeably out of tune, but it's good enough for this application.

The note frequency ROM.

The image above shows the scale ROM, configured to produce the notes G₄ through C₆ in the key of C. (Different versions of the chip can generate different notes by changing the scale ROM.) As with the melody ROM, the binary values are generated by the wiring of the metal layer to the transistors. For instance, the note B₅ has the bits 0,1,0,0,1,0,1 (from bottom to top). Below the ROM, the decoder activates one of the 16 column lines based on the 4-bit note value. (Notice the binary pattern of transistors in the decoder: the top rows alternate, the next rows are every 2, then every 4 and every 8.

The chip uses an unusual technique to generate the output frequency. The standard way is to divide the clock frequency by the scale factor with a counter, but instead the chip has an unusual approach to save a few transistors. It uses a 7-bit linear-feedback shift register. The construction of the linear-feedback shift register is that the input is the XOR of the last two bits. It will cycle pseudo-randomly through all 127 values.4

The trick in the melody chip is to initialize the shift register with a particular value loaded from the ROM, and run through the sequence until the value 1000000 is reached. By picking the right starting value, the desired number of counts will be obtained. The diagram below illustrates the operation of the shift register with the B₅ input 0100101. With this starting value, it takes 34 steps to reach the final value of binary 1000000. Notice how the bits are shifted to the right each step, with a new bit inserted at the left.

0 1 0 0 1 0 1
1 0 1 0 0 1 0
1 1 0 1 0 0 1
1 1 1 0 1 0 0
0 1 1 1 0 1 0
1 0 1 1 1 0 1
1 1 0 1 1 1 0
1 1 1 0 1 1 1
0 1 1 1 0 1 1
0 0 1 1 1 0 1
1 0 0 1 1 1 0
1 1 0 0 1 1 1
0 1 1 0 0 1 1
0 0 1 1 0 0 1
1 0 0 1 1 0 0
0 1 0 0 1 1 0
1 0 1 0 0 1 1
0 1 0 1 0 0 1
1 0 1 0 1 0 0
0 1 0 1 0 1 0
1 0 1 0 1 0 1
1 1 0 1 0 1 0
1 1 1 0 1 0 1
1 1 1 1 0 1 0
1 1 1 1 1 0 1
1 1 1 1 1 1 0
1 1 1 1 1 1 1
0 1 1 1 1 1 1
0 0 1 1 1 1 1
0 0 0 1 1 1 1
0 0 0 0 1 1 1
0 0 0 0 0 1 1
0 0 0 0 0 0 1
1 0 0 0 0 0 0

Since this takes 34 steps, the clock frequency is divided by 34 and the output frequency is 32768 ÷ 34 = 963 Hertz, close to the desired frequency of 997 Hertz.3 For another example, G₄ starts with 1001010 and runs for 84 counts, yielding a frequency of 392 Hertz. Thus, the ROM controls the frequency of the notes produced. Note that the starting values are not obviously correlated with the frequency; they depend on the sequence generated by the linear feedback shift register. (This sequence is called pseudo-random since it is deterministic but appears kind of random.)

Next, I'll discuss the implementation of the shift register. The die photo below shows one stage of the shift register. It receives input from the stage below and passes its output to the stage above. The stage is constructed from 26 transistors: 13 PMOS transistors on the left and 13 NMOS transistors on the right. The transistors are oriented vertically along the pink regions of doped silicon. The transistor gates are where the metal lines widen. Note that transistors in a column are connected by the silicon.

Die photo showing one stage of the shift register.

The schematic below shows how the transistors are connected, corresponding to the die photo above.

Schematic of one stage of the shift register, corresponding to the die photo.

At a slightly higher level, the circuit consists of inverters and multiplexers5 as shown below. Each loop of two inverters holds a bit. The first multiplexer selects the input: either a value from the ROM that is loaded into the shift register, or the value from the previous stage. When the clock goes high, this value is loaded into the first inverter loop. When the clock goes low, the value in the first inverter loop is transferred to the second inverter loop, and thus the output. Thus, it takes one complete clock cycle (low then high) to shift a bit one stage in the shift register.

Schematic of one stage of the shift register.

The clock

The chip runs on a 64-kilohertz clock. This clock is generated from a simple resistor-capacitor-inverter oscillator inside the chip, avoiding the need for external components. Because the capacitor takes some time to charge through the resistor, the oscillation speed is controlled.

The die photo below shows a closeup of the oscillator. The white rectangle is the capacitor. The green zig-zag is the resistor. Note that the resistance can be adjusted by shorting out part of the resistor in the metal layer. The white zig zags are the gates of the inverter transistors. These transistors are larger than the typical logic transistors.

Die photo showing the clock circuitry.

The on-chip R-C oscillator is cheap but inaccurate, unlike a quartz crystal oscillator. If the voltage changes, the frequency changes. In the video below, I lower and raise the voltage, and you can hear the effect on the tunes as the frequency changes.

Timing

The 64-kilohertz clock goes through a divider chain to divide the frequency by 512. This divider is made of nine toggle flip-flops, each one dividing the frequency by 2. These flip-flops are built from inverters and multiplexers similar to the shift register flip-flops, but wired to toggle. This feeds the beat generator, which adjusts the timing for quarter notes, eighth notes, etc. It uses a linear-feedback shift register, similar to the tone generator, but with four shift register stages. The shift register is loaded with a value from the rhythm ROM that determines the length of the note.

The output from the beat generator goes to the tempo generator, which divides its input by a preset amount (1 to 15) to generate a tempo between 128 and 1920 beats per minute. The tempo generator is also a 4-bit linear feedback shift register. The input to the shift register is hard wired to set the fixed tempo. The photo below shows one stage, wired to 1. A small change to the metal layer would cause 0 to be connected instead of 1.

The tempo is programmed by wiring shift register inputs to either 0 or 1.

The program counter counts through the 64 notes, providing the address to the melody ROM. It is built from toggle flip-flops chained together to build a 6-bit counter. The flip-flops have a reset line to initialize the counter to 0 at the start. The chip has a few dozen logic gates to keep track of the current state, handle startup, test mode, and so forth.

Conclusion

This melody chip uses simple circuits to produce songs in a flexible way. The chip integrates all the necessary circuitry including the R-C oscillator, so only a battery and a speaker were required. Nowadays a microcontroller would be the easiest way to implement this. This 1980s chip, however, uses small ROMS and simple counters to produce the tunes. I'll end with a quote from John Nolan: "Nothing says 'Christmas' like decapitating a microchip that plays slightly off-key Christmas songs."

This article is the extension of my earlier Twitter thread, which had a bunch of discussion on Hacker News. I announce my latest blog posts on Twitter, so follow me @kenshirriff. I also have an RSS feed. Thanks to Mark Fraser for finding an article on the chip.6

Notes and references

1. The note codes range from 0010 for G4 through 1100 for C6, in the key of C. I wrote a short Python program to convert the ROM contents to notes. ↩

2. Datasheets for the UM66T are available here, here, and here. A die photo of a different UM66T version is on siliconpr0n; I think this one plays Für Elise. ↩

3. The output frequency is half what you might expect from the 64 kHz clock. To keep the waveform symmetrical, there is a toggle flip-flop on the output that divides the counter output by 2. ↩

4. The 7-bit LFSR has 127 values instead of 128 values because it will get stuck in the all-zero value (since 0⊕0 = 0). ↩

5. The multiplexers are built from a CMOS circuit called a transmission gate (below). A transmission gate operates as a switch. When enable is high, both transistors turn on, passing the signal through the gate. When enable is low, both transistors turn off, blocking the signal. (Note that the PMOS transistor has an inverted control signal.) A multiplexer is built from two transmission gates. The control signal is connected to the two transmission gates with opposite polarity, so one transmission gate will be active at a time. Thus, one of the inputs is selected.

   

   Schematic of a transmission gate.

    ↩

6. A 1988 article (p24-26) in Maplin Electronics described how to build a circuit with the UM66T.

   

   First page of the article from Maplin Electronics, March 1988.

    ↩

Yamaha DX7 chip reverse-engineering, part 4: how algorithms are implemented

The Yamaha DX7 digital synthesizer (1983) was the classic synthesizer in 1980s pop music. It uses two custom digital chips to generate sounds with a technique called FM synthesis, producing complex, harmonically-rich sounds. Each note was implemented with one of 32 different patterns of modulation and summing, called algorithms. In this blog post, I look inside the sound chip and explain how the algorithms were implemented.

Die photo of the YM21280 chip with the main functional blocks labeled. Click this photo (or any other) for a larger version.

The die photo above shows the DX7's OPS sound synthesis chip under the microscope, showing its complex silicon circuitry. Unlike modern chips, this chip has just one layer of metal, visible as the whitish lines on top. Around the edges, you can see the 64 bond wires attached to pads; these connect the silicon die to the chip's 64 pins. In this blog post, I'm focusing on the highlighted functional blocks: the operator computation circuitry that combines the oscillators, and the algorithm ROM that defines the different algorithms. I'll outline the other functional blocks briefly. Each of the 96 oscillators has a phase accumulator used to generate the frequency. The sine and exponential functions are implemented with lookup tables in ROMs. Other functional blocks apply the envelope, hold configuration data, and buffer the output values.

The DX7 was the first commercially successful digital synthesizer, using a radically new way of generating sounds. Instead of the analog oscillators and filters of an analog synthesizer, the DX7 generates sounds digitally, using a technique called FM synthesis. The idea is that you start with a sine wave (the carrier signal) and perturb it with another signal (the modulating signal). The modulating signal changes the phase (and thus the frequency) of the carrier, creating complex harmonic structures. The custom chips inside the DX7 made this possible at an affordable price.

The DX7 synthesizer. Photo by rockheim (CC BY-NC-SA 2.0).

FM synthesis

I'll briefly explain how FM synthesis is implemented.1 The DX7 supports 16 simultaneous notes, with 6 operators (oscillators) for each note, 96 oscillators in total. However, to minimize the hardware requirements, the DX7 only has a single digital oscillator circuit. This circuit calculates each operator individually, in sequence. Thus, it takes 96 clock cycles to update all the sounds. To keep track of each oscillator, the DX7 stores 96 phase values, an index into the sine wave table. By incrementing the index at a particular rate, a sine wave is produced at the desired frequency.

The idea of FM synthesis is to modulate the index into the sine wave table; by perturbing the index, the output sine wave is modified. The diagram below shows the effects of modulation. The top curve shows a sine wave, generated by stepping through the sine wave table at a fixed rate. The second curve shows the effects of a small amount of modulation, perturbing the index into the table. This distorts the sine wave, compressing and stretching it. The third curve shows the effects of a large amount of modulation. The index now sweeps back and forth across the entire table, distorting the sine wave unrecognizably. As you can see, modulation can produce very complex waveforms. These waveforms have a rich harmonic structure, yielding the characteristic sound of the DX7. (I made a webpage here where you can experiment with the effects of modulation.)

Modulation examples. The top sine wave is unmodulated. The middle wave has a small amount of modulation. The bottom wave is highly modulated.

Algorithms

The above section illustrated how two oscillators can be combined with modulation. The DX7 extends this principle, generating a note by combining six oscillators through modulation and summing. It implements 32 different ways of combining these oscillators, illustrated below, and calls each one an algorithm. The different algorithms provide flexibility and variety in sound creation. Multiple levels of modulation create harmonically-rich sounds. On the other hand, multiple output operators allow different sounds to be combined. An electric piano sound, for example, could have one sound for the hammer thud, a second sound for the body of the tone, and a third sound for the ringing tine, all varying over time.

The 32 algorithms of the DX7 synthesizer.

Looking at algorithm #8, for example, shows the structure of an algorithm. Each box represents an operator (oscillator). Operators 1 and 3 (in blue), are combined to form the output. The remaining operators provide modulation, as indicated by the lines. Operator 2 modulates operator 1. Operators 4 and 5 are combined to modulate operator 3, providing a complex modulation. Operator 6, in turn, modulates operator 5. Finally, the line looping around operator 4 indicates that operator 4 modulates itself. Since each modulation level can vary over time, the resulting sound can be very complex.

Algorithm 8 combines the six operators; two produce outputs.

Shift-register storage

To understand the DX7's architecture, it's important to know that the chip uses shift registers, rather than RAM, for its storage. The idea is that bits are shifted from stage to stage each clock cycle. When a bit reaches the end of the shift register, it can be fed back into the register or a new bit can be inserted. For the phase accumulators, the shift registers are 96 bits long since there are 96 oscillators. Other circuits use 16 bit-shift registers to hold values for the 16 voices. The shift register circuitry (below) is dense, but even so, it takes up a large fraction of the chip.

A small part of the shift register storage.

The use of shift registers greatly affects the design of the DX7 chip. In particular, values cannot be accessed arbitrarily, as in RAM. Instead, values can only be used when they exit the shift register, which makes the circuit design much more constrained. Moreover, circuits must be carefully designed so that each path of a computation takes the same number of cycles (e.g. 16 cycles). Shorter paths must be delayed as necessary.2

I want to emphasize how unusual this chip is, compared to a microprocessor. You might expect that an algorithm is implemented with code, for example reading operator 2, applying modulation to operator 1, and then storing the result in operator 1. Instead, computation happens continuously in the chip, with data moving into the circuitry every clock cycle as it comes from the shift registers. The chip is more like an assembly line with bits constantly moving on many conveyor belts, and circuits steadily operating on bits as they move by. An advantage of this approach is that every clock cycle, calculations happen in parallel in multiple parts of the chip, providing much higher performance than a microprocessor could in the 1980s.

Implementation of the algorithms

The block diagram below shows the overall structure of the OPS sound chip. The idea is that the envelope chip (EGS) constantly provides frequency (F) and envelope control (EC) values at the top. The DX7's control CPU updates the algorithm (A) if the user selects a new one. The sound chip generates digital data (DA) for the 16 voices, which is fed out at the right. (The DX7's digital-to-analog converter circuitry (DAC) converts these digital values to the analog sound from the synthesizer.)

Diagram showing the architecture of the OPS chip, from the DX7/9 Service Manual.

In more detail, the circuitry in the upper left generates the phase values for the 96 oscillators and looks up the values in the sine wave table. In the lower-left, the highlighted block implements the algorithm, producing two outputs. This block contains its own storage: the memory (M) register and feedback (F) register. It generates a modulation value that modulates the index into the sine wave table. It also produces the digital sound value that is the output from the chip. (This highlighted block is the focus of this article.) At the right, the CPU specifies the algorithm number; the algorithm ROM specifies the algorithm by generating control signals COM, SEL, and so forth.

The DX7 has 96 oscillators, which are updated in sequence. The cycle of 96 updates takes place as shown below. In the first clock cycle, computation starts for operator 6 of voice (channel) 1. In the next clock cycles, operator 6 processing starts for voices 2 through 16. Next, operator 5 is processed for the 16 voices, and likewise for operators 4 to 1. At the end of this cycle, all the notes have been updated. Two factors are important here. First, operators are processed "backward", starting at 6 and ending at 1. Second, for a particular voice, there are 16 clock cycles between successive operators. This means that 16 cycles are available to compute each operator.

A complete processing cycle, as shown in the service manual. The overall update rate is 49.096 kHz providing reasonable coverage of the audio spectrum.

The diagram below provides more detail of highlighted block above, the circuitry that modulates the waveform according to a particular algorithm. The effect of modulation is to perturb the phase angle before lookup in the sine wave table.3 At the bottom right, the signal from operator N+1 enters, and is used to compute the modulation for operator N, exiting at the bottom left.

Diagram showing modulation computation, from the patent. Inconveniently, the signal names are inconsistent with the service manual.

The key component is the selector at the left, which selects one of the five modulation choices, based on the control signal S or SEL. Starting at the bottom of the selector, SEL=1 selects the unmodified signal from the input operator; this implements the straightforward modulation of an operator by another. Next, SEL=2 uses the value from the adder (61) for modulation. This allows an operator to be modulated by the sum of operators, for instance in algorithm 7. SEL=3 uses the delayed value from the buffer; this is used solely for algorithm 21, where operator 6 modulates operator 4. SEL=4 and SEL=5 use the self-feedback operator for modulation. Because the feedback value is buffered in the circuitry, it is available at any time, unlike other operators. SEL=4 is used to obtain delayed feedback, for instance when operator 6 modulates operator 4 in algorithm 19. (In most cases, feedback is applied immediately, for instance when operator 6 modulates operator 5, and this uses SEL=1.) SEL=5 handles the self-feedback case; the previous two feedback values are averaged to provide stability.4 The SEL=0 case is not shown; it causes no modulation to be selected so the operator is unmodulated.

Several control signals (A, B, C, D, E) also control the circuit. (Confusingly, the patent diagram below uses the names A and B for the feedback register enable (FREN) line. The memory register enable (MREN) lines are called C and D.) Signals A and B have the same value: they select if the feedback buffer continues to hold the previous value or loads a new value. Signals C and D control the buffer/sum shift register. If C is 1 and D is 0, the register holds its previous value. If C is 0 and D is 1, the input signal is loaded into the register. If both C and D are 1, the input signal is added to the previous value. This register can be used to sum two modulation signals, as in algorithm 7. But it is also used to hold and sum the output signals. (As a consequence, an algorithm can't sum modulation signals and outputs at the same time.) Signal E loads the algorithm's final output value into the output buffer (70). Signal E and buffer 70 are implemented separately, so I won't discuss them further.

The algorithm ROM

The algorithms are defined by a ROM with 9-bit entries that hold the selector value (SEL), the control signals MREN and FREN (A,C,D), and the compensation scaling value COM (which I explain later). Each algorithm needs 6 entries in the ROM to select the action for the 6 operators. Thus, the ROM holds 96 9-bit values.

The photo below shows the algorithm ROM. It has 32 columns, one for each algorithm and 9 groups of 6 rows: one group for each output bit. From bottom to top, the outputs are three bits for the selector value SEL, two MREN lines and the FREN line, and three bits for the COM value. The groups of 6 diagonal transistors at the left of the ROM select the entry for the current operator.

The algorithm ROM. The metal layer has been removed to show the silicon structure underneath that defines the bits.

The bits are visible in the pattern of the ROM. By examining the ROM closely, I extracted the ROM data. Each entry is formatted as "SEL / A,C,D / COM". (I only show three entries below; the full ROM is in the footnotes.5)

	Operator
Algorithm	6	5	4	3	2	1
1	1/100/0	1/000/0	1/000/1	0/001/0	1/010/1	5/011/0
2	1/000/0	1/000/0	1/000/1	5/001/0	1/110/1	0/011/0
	...
8	1/000/0	5/001/0	2/111/1	0/001/0	1/010/1	0/011/0

To see how an algorithm is implemented, consider operator 8, for instance.6

Algorithm 8 has four modulators and two carriers.

Processing of an algorithm starts with operator 6's signal value at the output of the operator block and operator 5's modulation is being computed. Table column 6 above shows SEL=1, A,C,D=000. In the modulation circuit (below), SEL=1 selects the raw signal in (i.e. operator 6's value) for modulation. Thus, operator 6 modulates operator 5, the desired behavior for algorithm 8.

Diagram showing modulation computation.

Next, (16 cycles later), operator 5's signal is at the output and operator 4's modulation is being computed. Column 5 of the table shows SEL=5, A,C,D=001. SEL=5 selects the filtered feedback register for self-modulation of operator 4. D=1 causes operator 5's value to be loaded into the shift register, in preparation for modulating operator 3.

Next, operator 4's signal is at the output and operator 3's modulation is being computed. Column 4 shows SEL=2 and A,C,D=111. Bits A (and B) are 1 to load the feedback register with operator 4's value, updating the self-feedback for operator 4. Bits C and D cause operator 4 to be added to the previously-stored operator 5 value. SEL=2 selects this sum for operator 3's modulation, so operator 3 is modulated by both operators 4 and 5. COM=1 indicates this operator is one of 2 outputs, so operator 3's value will be divided by 2 as it is computed.

Next, operator 3's signal is at the output and operator 2's modulation is being computed. Looking at the ROM, SEL=0 results in no modulation of operator 2. D=1 loads operator 3's signal into the summing shift register, in preparation for the output.

Next, operator 2's signal is at the output and operator 1's modulation is being computed. SEL=1 causes operator 1 to be modulated by operator 2. C=1 so the summing shift register continues to hold the operator 3 value, to produce the output. As with operator 3, COM=1 so operator 1's value will be divided by 2 when it is computed.

Finally, operator 1's signal is at the output and operator 6's modulation is being computed. SEL=0 indicates no modulation of operator 6. Control signals C and D are 1 so operator 1 is added to the register (which holds operator 3's value), forming the final output.

This process repeats cyclically, interleaved with processing for the 15 other voices. This section illustrates how a complex algorithm is implemented through the modulator circuitry, directed by a few control signals from the ROM. The other algorithms are implemented in similar ways.7

The modulation circuitry

The diagram below shows the circuitry that computes the modulation and output; this functional block is in the center of the chip. The memory register (red) holds 16 values, one for each voice. To its right, the adder (blue) adds to the value in the memory register. The selector (purple), is the heart of the circuit, selecting which value is used for modulation. It is controlled by the selector decoder (orange) at the bottom, which activates a control line based on the 3-bit SEL value. At the far right, the two feedback registers (red) hold the last two feedback values for each of the 16 voices. The feedback adder sums two feedback values to obtain the average. The feedback shifter (yellow) scales the feedback value by a power of 2.

The circuitry that calculates the modulation for the algorithm.

Shift registers

The schematic below shows how one stage of the shift register is implemented. The chip uses a two-phase clock. In the first phase, clock ϕ1 goes high, turning on the first transistor. The input signal goes through the inverter, through the transistor, and the voltage is stored in the capacitor. In the second phase, clock ϕ2 goes high, turning on the second transistor. The value stored in the capacitor goes through the second inverter, through the second transistor, and to the output, where it enters the next shift register stage. Thus, in one clock cycle (ϕ1 and then ϕ2), the input bit is transferred to the output. (The circuit is similar to dynamic RAM in the sense that bits are stored in capacitors. The clock needs to cycle before the charge on the capacitor drains away and data is lost. The inverters amplify and regenerate the bit at each stage.)

Schematic of one stage of the shift register.

The diagram below shows part of the shift register circuitry as it appears on the die. The blue rectangle indicates one shift register stage. The power, ground, and clock wiring is in the metal layer, which was mostly removed in this image. Shift register stages are linked horizontally. Shift registers for separate bits are stacked vertically, with alternating rows mirrored.

Die photo showing a stage of the shift register.

The selector

The selector circuit selects one of the five potential multiplexer values, based on the SEL input. The circuit uses five pass transistors (indicated in yellow) that pass one of the 5 inputs to the driver circuit and then the output. (A sixth transistor pulls the output high if none of the inputs is selected; I've labeled this "x".) The diagram below shows one selector in the top half, and a mirror-image selector below; there are 12 selector circuits in total. The circuit is built around the six vertical select lines. One select line is activated to select a particular value. This turns on the corresponding transistors, allowing that input to flow through the transistors. The result goes through another transistor to synchronize it to the clock, and then an inverter/buffer to drive the output line. The outputs go to the sine-wave circuit, where they modulate the input to the lookup table.

Two stages of the selector.

The adder

The chip contains multiple adders. Two adders are used in the modulation computation: one to sum operators and one to average the two previous feedback values. The adders are implemented with a standard binary circuit called a full adder. A full adder takes two input bits and a carry-in bit. It adds these bits to generate a sum bit and a carry-out bit. By combining full adders, larger binary numbers can be added.

Diagram showing a full adder.

The diagram above shows a full adder stage in the chip. The circuit is built from three relatively complex gates, but if you try the various input combinations, you can see that produces the sum and carry. (Due to the properties of NMOS circuits, it's more efficient to use a small number of complex gates rather than a larger number of simple gates such as NAND gates.)

One problem with binary addition is that it can be relatively slow for carries to propagate through all the stages. (This is the binary equivalent of 99999 + 1.) The solution used in the DX7 is pipelining: an addition operation is split across multiple clock cycles, rather than being completed in a single clock cycle. This reduces the number of carries in one clock cycle. Although a particular addition takes several clock cycles, the adders are kept busy with other additions, so one addition is completed every cycle.

The compensation (COM) computation

In the DX7, different algorithms have different numbers of oscillators in the output, which poses a problem An algorithm with 6 output oscillators (e.g. #32) would be six times as loud as an algorithm with 1 oscillator (e.g. #16), which would be annoying as the user changes the algorithm. To avoid this problem, the chip scales the level of output oscillators accordingly. For instance, the levels of output oscillators in algorithm #32 are scaled by 1/6 to even out the volumes. This factor is called COM (compensation) in the service manual and ADN (addition channel number) in the patent.8 To implement this scaling, the algorithm ROM holds the output count for each operator, minus 1. For example, algorithm #32 has six output oscillators, each one having a COM value of 5 (i.e. 6-1). For algorithm #1, the two output oscillators are 1 and 3: these have a COM value of 1 (i.e. 2-1). Operators that are used for modulation are not scaled, and have a COM value of 0.

Recall that the envelope scaling is accomplished by adding base-2 logarithms. The COM scaling also uses logarithms, which are subtracted to scale down the output level. A small ROM generates 6-bit logarithms for the COM values 1 through 5, corresponding to scale factors 2 through 6. The diagram below shows the COM circuitry, which is in the upper-right corner of the chip. At the left, the decoder and tiny ROM determine the logarithmic scaling factor from the number of inputs. This is added to the logarithmic envelope level that the chip receives from the envelope chip. The result goes through a few shift register stages for timing reasons.

The COM circuitry adds a compensation level to the envelope to compensate for algorithms with multiple outputs.

Conclusion

The DX7's algorithm implementation circuitry is at the heart of the chip's sound generation. This circuitry is cleverly designed to implement 32 different algorithms at high speed with the limited hardware of the 1980s. The circuitry runs fast enough to process 16 voices sequentially, each with 6 separate oscillators, while producing outputs fast enough to produce audio signals. By taking advantage of the pipelined architecture built around shift registers, the chip processes a different oscillator during each clock cycle, a remarkable throughput. Overall, I'm impressed with the design of this chip. Its cutting-edge design was the key to the DX7's ability to provide dramatic new sounds at a low price. As a result, the DX7 defined the canonical sound of the 1980s and changed the direction of pop music.

I plan to continue investigating the DX7's circuitry, so follow me on Twitter @kenshirriff for updates. I also have an RSS feed. Also see my previous posts on the DX7: DX7 reverse-engineering, the exponential ROM, The log-sine ROM.

Thanks to Jacques Mattheij and Anthony Richardson for providing the chip and discussion.9

Notes and references

1. Note that the underlying frequency of the oscillator stays the same during modulation, but the phase is changed. Technically the DX7 uses phase modulation (PM) rather than frequency modulation (FM). The two are closely related—phase modulation with a signal is the same as frequency modulation with the derivative of the signal—so the difference is usually ignored. ↩

2. Another complication is that the chip is pipelined. It doesn't simply go through 96 clock cycles, updating one operator each cycle. Instead, the computations for an operator are spread across multiple clock cycles. The result is still that one operator calculation is completed per clock, but different parts of the circuitry are working on different operators at any particular time.

   The reason for pipelining is to handle calculations that won't fit into one clock cycle. For instance, the chip adds 22-bit numbers. Propagating a carry through all 22 adder stages would take too long for one clock cycle. Instead, addition takes place in chunks of about 4 bits. The lowest 4 bits are added in one clock cycle, the next bits in the next clock cycle, and so forth. Thus, the propagation delay during one clock cycle is substantially reduced. The circuit still completes one addition per cycle, even though any particular addition takes multiple cycles. ↩

3. The diagram below from the patent shows how this is implemented. The modulation is added to the phase angle to create the index into the sine table, yielding the modulated signal. This signal is scaled by the envelope; instead of multiplying, the base-2 logarithms of both values are added. (Ignore ADN for now; I'll discuss it later.) Finally, the logs are converted back to linear values by an exponential ROM and circuit. The result is the modulated and scaled output signal. The steps in this box take exactly 16 clock cycles, which will turn out to be important. As a result, operator N's values enter the box at the same time that operator N+1's values exit the box. (Remember that operators are processed in reverse order: 6 down to 1.)

   

   Diagram showing the construction of an operator, from the patent.

   I'll summarize the patent's mathematical notation in case anyone reads it. The phase angle, varying with time is ωt. kωt indicates the possible use of a frequency modifier k. The modulation function is f(ω_mt), a function of the modulation frequency. The envelope, as a function of t, is A(t) for the amplitude or I(t) for the modulation index; that is, applied to an output operator or a modulating operator respectively. On the diagrams, Φ indicates the clock. ↩

4. When an operator provides feedback to itself (usually operator 6), the modulation uses a special path that averages the previous two values. The patent calls this an "anti-hunting" feature. I think this avoids wild oscillations from self-feedback. Suppose you have a situation where a large modulation signal produces a small output and a small modulation signal produces a large output. This would result in the signal oscillating between small and large every clock cycle, which would be unpleasant. Averaging the previous two values is essentially a low-pass filter and would prevent these wild oscillations. Also note that the self-feedback path allows the feedback level to be controlled by the FBL signal. This shifts the feedback signal, dividing it by a power of 2. ↩

5. The full algorithm ROM contents are below. The format is "SEL/ FREN MREN / COM value". Note that algorithm numbers are 1 to 32, while the ROM's binary addresses are 0 to 31.

   	Operator
   Algorithm	6	5	4	3	2	1
   1	1/100/0	1/000/0	1/000/1	0/001/0	1/010/1	5/011/0
   2	1/000/0	1/000/0	1/000/1	5/001/0	1/110/1	0/011/0
   3	1/100/0	1/000/1	0/001/0	1/010/0	1/010/1	5/011/0
   4	1/000/0	1/000/1	0/101/0	1/010/0	1/010/1	5/011/0
   5	1/100/2	0/001/0	1/010/2	0/011/0	1/010/2	5/011/0
   6	1/000/2	0/101/0	1/010/2	0/011/0	1/010/2	5/011/0
   7	1/100/0	0/001/0	2/011/1	0/001/0	1/010/1	5/011/0
   8	1/000/0	5/001/0	2/111/1	0/001/0	1/010/1	0/011/0
   9	1/000/0	0/001/0	2/011/1	5/001/0	1/110/1	0/011/0
   10	0/001/0	2/011/1	5/001/0	1/110/0	1/010/1	0/011/0
   11	0/101/0	2/011/1	0/001/0	1/010/0	1/010/1	5/011/0
   12	0/001/0	0/011/0	2/011/1	5/001/0	1/110/1	0/011/0
   13	0/101/0	0/011/0	2/011/1	0/001/0	1/010/1	5/011/0
   14	0/101/0	2/011/0	1/000/1	0/001/0	1/010/1	5/011/0
   15	0/001/0	2/011/0	1/000/1	5/001/0	1/110/1	0/011/0
   16	1/100/0	0/001/0	1/010/0	0/011/0	2/011/0	5/001/0
   17	1/000/0	0/001/0	1/010/0	5/011/0	2/111/0	0/001/0
   18	1/000/0	1/000/0	5/001/0	0/111/0	2/011/0	0/001/0
   19	1/100/2	4/001/2	0/011/0	1/010/0	1/010/2	5/011/0
   20	0/001/0	2/011/2	5/001/0	1/110/2	4/011/2	0/011/0
   21	1/001/3	3/001/3	5/011/0	1/110/3	4/011/3	0/011/0
   22	1/100/3	4/001/3	4/011/3	0/011/0	1/010/3	5/011/0
   23	1/100/3	4/001/3	0/011/0	1/010/3	0/011/3	5/011/0
   24	1/100/4	4/001/4	4/011/4	0/011/4	0/011/4	5/011/0
   25	1/100/4	4/001/4	0/011/4	0/011/4	0/011/4	5/011/0
   26	0/101/0	2/011/2	0/001/0	1/010/2	0/011/2	5/011/0
   27	0/001/0	2/011/2	5/001/0	1/110/2	0/011/2	0/011/0
   28	5/001/0	1/110/0	1/010/2	0/011/0	1/010/2	0/011/2
   29	1/100/3	0/001/0	1/010/3	0/011/3	0/011/3	5/011/0
   30	5/001/0	1/110/0	1/010/3	0/011/3	0/011/3	0/011/3
   31	1/100/4	0/001/4	0/011/4	0/011/4	0/011/4	5/011/0
   32	0/101/5	0/011/5	0/011/5	0/011/5	0/011/5	5/011/5

    ↩

6. The DX7/9 service manual explains the steps of algorithms 1 and 21 in detail. ↩

7. Note that the algorithms are carefully designed with operator 6 on top and 1 on the bottom, so operators are modulated only by operators with a higher number. This is due to the implementation of the modulation circuitry which processes operators starting with 6 and ending with 1. The 32 algorithms make it look like almost anything is possible, but the hardware imposes several constraints that limit the possibilities. For instance, there is only one sum/delay register so you can't sum modulators and the output at the same time. You can't delay a non-feedback operator after an output takes place; for instance, algorithm 11 has 6 delayed to modulate 3, but only because there haven't been any outputs at that point. An algorithm can only have one self-feedback loop. ↩

8. The logarithmic COM values are:

   COM	binary value	value
   0	00.000	log2(1)
   1	01.000	log2(2)
   2	01.101	≈log2(3)
   3	10.000	log2(4)
   4	10.011	≈log2(5)
   5	10.101	≈log2(6)

   Since the computation is done with logarithms, the circuit subtracts these values (or equivalently adds the complement). This is equivalent to dividing by the number of outputs or multiplying by the reciprocal. Note that the COM input is one less than the number of outputs. Entry 0 is not explicitly stored in the ROM but results by default. If the result of the subtraction is negative, gates clamp the envelope at 0. ↩

9. For more information on the DX7 internals, see DX7 Technical Analysis, DX7 Hardware, OPLx decapsulated, and the video Emulating the DX7 the hard way. ↩

Yamaha DX7 reverse-engineering, part III: Inside the log-sine ROM

The Yamaha DX7 digital synthesizer (1983) was the classic synthesizer for 1980s pop music. It used two custom digital chips to generate sounds with FM synthesis. In this blog post, I examine the log-sine ROM that digitally produces sine waves inside one of these chips. (This blog post jumps into the details; unless you care about the sine values specifically, my previous DX7 reverse-engineering article is probably more interesting.)

I created the high-resolution die photo below by compositing over a hundred microscope photos. I removed the metal layer from the chip with acid to reveal the silicon and polysilicon wiring underneath. You can see the structure of the functional blocks and the connections between them. The colors are due to variations in thickness of the oxide layer, causing thin-film interference. With the metal layer removed, I could read out the bits from the ROM, reverse-engineer the circuitry, and determine the exact values used for sine-wave generation.

Die photo of the DX7's YM21280 Operator chip. Click this photo (or any other) for a magnified version.

Instead of the analog oscillators and filters of an analog synthesizer, the DX7 generates sounds digitally, using a technique called FM synthesis. The idea is that you start with a sine wave (the carrier signal) and perturb it with another signal (the modulating signal). The modulating signal changes the phase (and thus the frequency) of the carrier, creating complex harmonic structures like the waveform below. These signals are represented as digital values throughout the system; a digital-to-analog converter (DAC) turns the digital representation into an analog voltage for the synthesizer's output.

An example of a complex waveform created by FM synthesis. (I made a tool that lets you experiment with FM synthesis.)

The digital implementation of frequency modulation uses a lookup table that holds a digitized sine wave. By stepping an index through the table at a specific rate, you can produce a sine wave of a fixed frequency. By perturbing this index with another signal, you can produce a modulated sine wave like the one below. The DX7 implements this with a sine-wave table in ROM, an increment value that controls the frequency, and an adder that adds the increment to the table index (i.e. the phase angle) each time step. This ROM is the subject of this blog post.

The amplitude of the sine wave is controlled by an envelope, varying over time; multiplying the sine wave by the envelope level yields the output. However, fast multiplication required too much hardware in the 1980s, so the DX7 uses a mathematical shortcut: adding logarithms is equivalent to multiplying the values. The obvious problem is that computing logarithms is harder than multiplying, but the trick is to store the (negated) logarithm of the sine wave in the lookup table (below) instead of the sine wave. This provides the logarithm for free. (The other issue is that you need to perform an exponential to get the final result. I described the exponential ROM and circuit in my previous DX7 article).

This graph shows the log-sine function over one quarter of the wave, as a 14-bit value. It's not recognizable as a sine function, but will turn into a sine wave after exponentiation.

The block diagram below shows the structure of the log-sine circuit, computing a 14-bit value from a 12-bit input. The circuitry is somewhat complex to fit a fast, high-accuracy calculation into a small space on the die. The implementation takes advantage of the symmetry of the sine wave so only a quarter-wave needs to be stored. The top bit is used as the sign bit, which inverts the output elsewhere to obtain the negative half of the sine wave. (This also avoids the problem of taking the log of a negative value.) The second bit implements the mirror symmetry of each sine-wave peak by inverting the bits for the second half of the peak.

Block diagram of the sine circuit. Input bits are indicated in green.

The ROM and associated logic take a 10-bit input address representing a quarter of the sine wave (angles 0 through π/2). A technique called delta encoding is used to reduce the size of the ROM. The idea of delta encoding is that if values change slowly, the difference between two values is considerably smaller than the value itself.1 Specifically, only every fourth value is explicitly stored in the ROM; this value is called an "absolute" value.3 The next three values are stored as deltas: the difference between the value and the previous absolute value.2 An adder circuit adds the absolute value to the difference value, yielding the desired log-sin value.

The diagram below labels the main functional blocks of the chip. In this article, I focus on the sine circuit, highlighted in red, but I'll summarize the other blocks. The 96 phase accumulators, implemented with shift registers, are the largest block of the chip. They hold the current table index for each of the DX7's 96 oscillators. The exponential function is implemented by two identical ROMs and associated addition/shifter circuitry. Other major blocks apply the envelope, hold configuration data, compute the operators that combine oscillators, define different operator algorithms, and buffer the output values.

Die with the major functional blocks labeled. This photo shows the metal layer of the chip. (Click for a larger version.)

The ROM

The photo below shows the log-sin ROM. The ROM itself consists of a grid of transistors. At the top, decoder circuits select signal lines based on the address bits. At the right, the diagonal circuits are multiplexers, selecting particular rows of the ROM. To the right of the multiplexers, logic circuits select the delta values. I won't explain these circuits in detail since I discussed the similar circuits for the exponential ROMs in my previous article.

High-resolution image of the sine ROM. Click this image (or any other) for an enlarged image.)

By examining the ROM closely, you can see the individual transistors that store bits. A transistor represents a 1, and the lack of a transistor represents a 0. Thus, the data in the ROM is created by the pattern of how the silicon is doped. I was able to read out the ROM data visually by looking at this pattern.

Closeup of the ROM.

The delta representation and the adder

The ROM itself produces 43 output bits, 13 bits for the "absolute" value and 30 bits for the three delta values. Some logic circuitry expands the ROM's 30 bits into three deltas of 12 bits (and a zero delta for the absolute value), taking advantage of some structure in the deltas. This circuitry is just to the right of the ROM and is implemented with AND-OR-INVERT gates. These gates implement 4-to-1 multiplexers, selecting the appropriate delta value based on the 2 lowest input bits.

Next, the adder circuit to the right of the ROM adds the 13-bit absolute value and the 12-bit delta value to generate the final 14-bit value. One interesting feature of the adder is it is pipelined to minimize the delay from carry propagation. I discussed the adder implementation in my previous article so I won't go into details here. The adder is immediately followed by a second adder that adds the envelope value to scale the signal level, taking advantage of the logarithmic representation.

Overall, the log-sine circuit generates 1024 14-bit values. Stored directly, this would take over 14 kilobits, but the ROM is only 5344 bits. The delta representation and ROM compression reduce the ROM size by almost 63%, important for a chip built in the 1980s when transistors were precious. By itself, the delta representation doesn't save much space: a 12-bit delta instead of a 14-bit value. But the ROM's implementation makes the deltas efficient: if a 32-bit row in the ROM is all zeroes, the row can be omitted entirely and the output defaults to 0. For the flat parts of the function, the high-order bits of the deltas are mostly zero, so much of the ROM can be omitted.

Conclusion

The DX7 generates its waveforms from a digital sine wave, so producing a high-accuracy value rapidly is key to the synthesizer's performance. By examining the ROM and associated circuitry, I could obtain the exact values that the DX7 uses for the log-sine function. The ROM provides one quarter of the sine wave and the other quarters are formed by symmetry. For a 10-bit input value n, the corresponding angle is ω = (n + .5)/1024×π/24 and output value y is -log₂(sin(ω)), represented as the integer round(y×1024).5

The DX7's OPS chip comes in a 64-pin ceramic package with staggered pins. This is known as a Quad Inline Package (QIP). Photo courtesy of Jacques Mattheij.

I plan to continue investigating the DX7's circuitry, so follow me on Twitter @kenshirriff for updates. I also have an RSS feed.

Thanks to Jacques Mattheij and Anthony Richardson for providing the chip and discussion.6

Notes and references

1. A different chip, the Yamaha YMF262 (1988) was used in computer sound cards such as the Sound Blaster 16. (This chip is also known as OPL3 for FM Operator Type-L.) It uses FM synthesis, but is stripped down compared to the DX-7. The chip was reverse-engineered by Matthew Gambrell and Olli Niemitalo who decapsulated the chip and read out the ROM contents.

   The OPL3 log-sine ROM is similar to the DX7's in some ways, but is lower resolution. The OPL3 chip is 256 samples long, rather than 1024, and holds 8-bit values, rather than 13-bit values. Both chips use delta encoding, but the OPL3 has one delta-encoded value for each absolute value, while the DX7 has three delta-encoded values. ↩

2. To be precise, the three delta values are stored before the absolute value in the ROM. That is, entries 3, 7, 11, ... are absolute, instead of 0, 4, 8, ..., the expected locations. I think this is because the log-sin function is decreasing, so if you want to add the deltas (instead of subtracting), the absolute value needs to be the last of the group, not the first. ↩

3. The absolute value in delta encoding is the full, explicit value. It's unrelated to the absolute value function |x|. ↩

4. Note that the input to the ROM is incremented by half a bit. This avoids duplication of the 0 value of the waveform when the quarter-wave is mirrored. It also avoids computation of the undefined value log(0). ↩

5. The value is rounded to an integer by computing int(y×1024 + .5002). The constant .5002 rounds the value up, with just a tiny bit more that affects a single entry. I'm not sure why the rounding is not exact; perhaps Yamaha used a lower-precision sine or logarithm, which was just enough to change one bit. (Note that the value .0002 is somewhat arbitrary; a slightly larger or smaller number will yield the same result.) ↩

6. For more information on the DX7 internals, see DX7 Technical Analysis, DX7 Hardware, OPLx decapsulated, and my previous DX7 articles Reverse-engineering the Yamaha DX7 synthesizer's sound chip from die photos and The Yamaha DX7's exponential circuit. ↩