Qui-binary arithmetic: how a 1960s IBM mainframe does math

The IBM 1401 computer uses an unusual technique called qui-binary arithmetic to perform arithmetic. In the early 1960s, the IBM 1401 was the most popular computer, used by many businesses for the low monthly price of $2500. For a business computer, error detection was critical: if a company sent out bad payroll checks because of a hardware fault, it would be catastrophic. By using qui-binary arithmetic, the IBM 1401 detects arithmetic errors.

If you've studied digital circuits, you've seen the standard binary adder circuits that add two numbers. But the IBM 1401 uses a totally different approach. Unlike modern computers, the IBM 1401 operates on decimal digits, not binary numbers, using BCD (binary-coded decimal). To add two numbers, digits are converted from BCD to qui-binary, added together with a special qui-binary adder, and then converted back to digits in BCD. This may seem pointlessly complex, but it allows easy error detection.

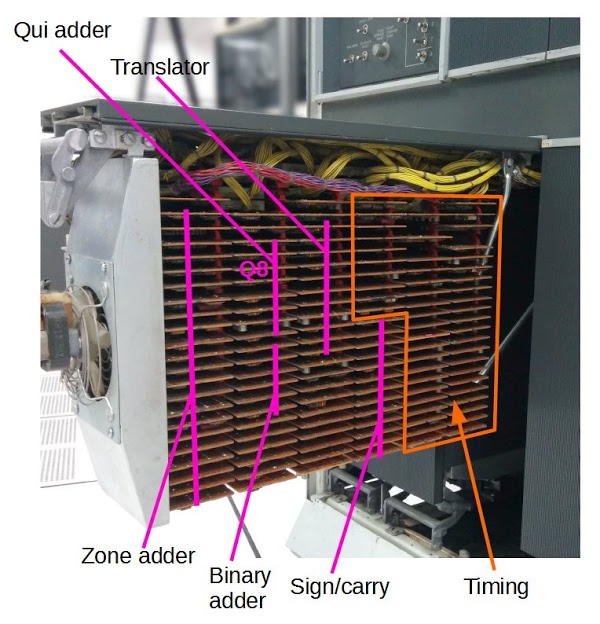
The photo below shows the IBM 1401 with one panel opened to show the addition/subtraction circuitry, made up of dozens of Standard Module System (SMS) cards. Each SMS card holds a simple circuit with a few germanium transistors (the computer predates silicon transistors). This article explains in detail how these circuits implement it.

The IBM 1401 mainframe with gate 01B3 opened. This gate contains the arithmetic circuitry, made up of many SMS cards.

What is qui-binary?

Qui-binary code is a way of representing a decimal digit with 7 bits. The number is split into a qui part (0, 2, 4, 6, or 8) and a binary part (0 or 1).[1] For example, 3 is split into 2+1, and 8 is split into 8+0. The qui part is labeled Q0, Q2, Q4, Q6, or Q8 and the binary part is B0 or B1. The number is then represented by seven bits: Q₈Q₆Q₄Q₂Q₀B₁B₀. The following table summarizes the qui-binary representation.

Digit	Qui	Binary	Bits: Q8Q6Q4Q2Q0B1B0
0	Q0	B0	0000101
1	Q0	B1	0000110
2	Q2	B0	0001001
3	Q2	B1	0001010
4	Q4	B0	0010001
5	Q4	B1	0010010
6	Q6	B0	0100001
7	Q6	B1	0100010
8	Q8	B0	1000001
9	Q8	B1	1000010

The advantage of qui-binary is error detection, since it is straightforward to detect an invalid qui-binary number.[2] A valid qui-binary number has exactly one qui bit and exactly one binary bit. Any other qui-binary number is faulty. For instance, Q4 Q2 B0 is bad, as is Q8. A problem in any bit creates a bad qui-binary number and can be detected.

Overview of the 1401's qui-binary circuit

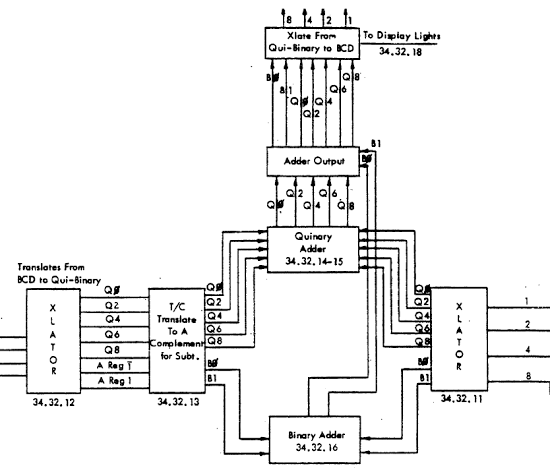
The IBM 1401's arithmetic unit operates on one digit at a time, adding them with a qui-binary adder.[3] The block diagram below[4] shows how the adder takes two binary-coded decimal digits, stored in the A and B temporary registers, and produces their sum. The digit from the A register enters on the left, and is translated to qui-binary by the translation circuit (labeled XLATOR). This qui-binary value goes through a translate/complement circuit which is used for subtraction. The digit in the B register enters on the right and is also converted to qui-binary. The binary bits (B0/B1) are added by the binary adder at the bottom. The quinary values are added with a special quinary adder. The adder output circuit combines the quinary bits with any carry, generating the qui-binary result. Finally, the translation circuit at the top converts the qui-binary result back to a BCD digit, sending the BCD value to core memory and to the console display lights.[5]

Overview of the arithmetic unit in the IBM 1401 mainframe.

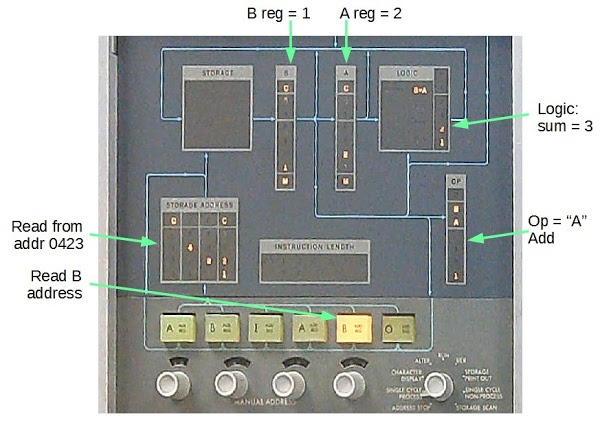
The photo below shows the IBM 1401 console during an addition instruction. The numbers are displayed in binary-coded decimal; the qui-binary representation is entirely hidden from the programmer. At this point in the addition instruction, the digit 1 was read from address 423 into the B register, and is added to the digit 2 already in the A register. The result from the qui-binary adder is 3 (binary 2 + 1), which is stored back to memory.[6]

The IBM 1401 console, showing an addition operation.

BCD to qui-binary translation

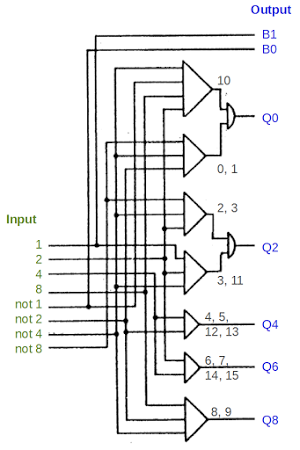
To examine the addition/subtraction circuitry in more detail, we'll start with the logic that converts a BCD digit to qui-binary. The logic is implement with an AND-OR structure that is common in the 1401. Note that the logic gate symbols are different from modern symbols: an AND gate is represented as a triangle, and an OR gate is represented as a semi-circle. Each bit of the BCD digit, as well as the bit's complement, is provided as input. Each AND gate matches a specific bit pattern, and then the results are combined with an OR gate to generate an output.

The circuit in an IBM 1401 mainframe to translate a BCD digit into qui-binary code.

To see how this works, look at the AND gate at the bottom (labeled 8, 9). Tracing the wires to the inputs, this gate will be active if input 8 AND input not-4 AND input not-2 are set, i.e. if the input is binary 1000 or 1001. Thus, output Q8 will be set if the input digit is 8 or 9, just as required for the qui-binary code.

For a slightly more complicated case, the first AND gate matches binary 1010 (decimal 10), and the second AND gate matches binary 000x (decimal 0 or 1). Thus, Q0 will be set for inputs 0, 1, or 10. Likewise, Q2 is set for inputs 2, 3, or 11. The other Q outputs are simpler, computed with a single AND gate.[7]

The B0 and B1 outputs are simply wires from the not-1 and 1 inputs. If the input is even, B0 is set, and if the input is odd, B1 is set.

9's complement circuit

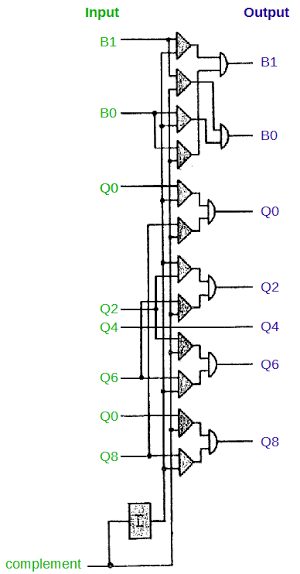
To perform subtraction, the IBM 1401 adds the 9's complement of the digit. The 9's complement is simply 9 minus the digit. The complement circuit below passes the qui-binary number through unchanged for addition or complemented for subtraction.[8] The complement input selects which mode to use; it is generated from the operation (addition or subtraction), and the signs of the input numbers.

To see how complementation works in qui-binary, consider 3 (Q2 B1). Its complement is 6 (Q6 B0). The general pattern for complementation is B0 and B1 get swapped. Q0 and Q8 are swapped, and Q2 and Q6 are swapped. Q4 is unchanged; for example, 4 (Q4 B0) is complemented to 5 (Q4 B1).[9]

The complement circuit from the IBM 1401 mainframe. This converts a digit to its 9's complement value.

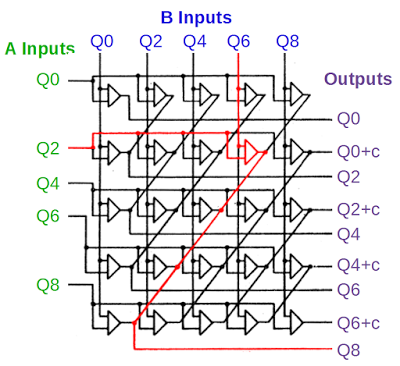
Quinary adder

The circuit below adds the quinary parts of the two numbers and can be considered the "meat" of the adder. The qui part from the A register is on the left, the qui part from the B register is on the top, and the qui output is on the right. The outputs with "+c" indicate a carry if the result is 10 or more. The addition logic is implemented with a "brute force" matrix, connecting each pair of inputs to the appropriate output. An example is Q2 + Q6, shown in red. If these two inputs are set, the indicated AND gate will trigger the Q8 output.[10]

The quinary addition circuit in the IBM 1401 mainframe. This adds the quinary parts of two qui-binary digits. Highlighted in red is the addition of Q2 and Q6 to form Q8.

In the photo below, we can find the exact card in the IBM 1401 that performs this addition. The card in the upper left marked with a red asterisk computes the output Q8.[11]

The SMS cards in the IBM 1401 that perform arithmetic.

The circuitry in the IBM 1401 is simple enough that you can follow it all the way to the function of individual transistors.[12] The asterisk-marked card is a 3JMX SMS card containing 4 AND gates, and is shown below. Each of the round metal transistors corresponds to one AND gate for one of the sums that generates the output Q8. The top transistor is activated by inputs 8+0, the next for 0+8, the next 6+2, and the bottom one 2+6. Thus, the bottom transistor corresponds to the red AND gate in the schematic above.[13]

The SMS card of type 3JMX has four AND gates.

Qui-binary to BCD translation

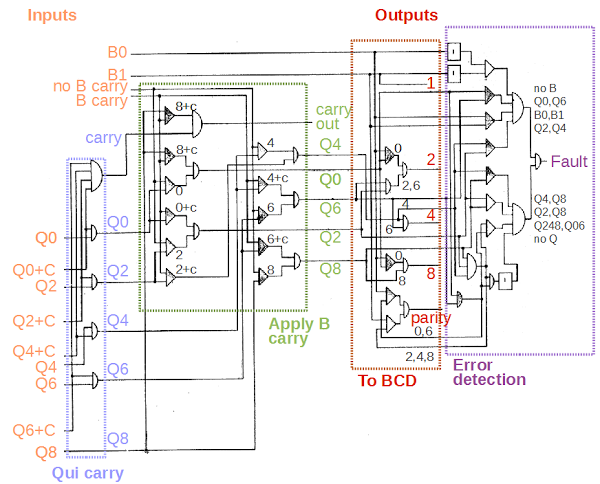
The diagram below shows the remainder of the qui-binary adder, which combines the qui and binary parts of the output, converts the output back to BCD, and detects errors. I'll just give an overview here, with more explanation in the footnotes.[14] The qui-binary carry circuit, in the blue box, processes the carry signals from the adder circuit. The next circuit, in the green box, applies any carry from the B bits, incrementing the qui component if necessary. The translation circuit, in red, converts the qui-binary result to BCD, using AND-OR logic. It also generates the parity output used for error detection in memory. The final circuit, in purple, is the error detection circuit which verifies the qui-binary result is valid and halts the computer if there is a fault.

The circuitry in the IBM 1401 mainframe to convert a qui-binary sum to a BCD result.

The photo below shows the functions of the different cards in the arithmetic rack.[15] The cards in the left half perform arithmetic operations. Each function takes multiple cards, since a single SMS card has a small amount of circuitry. "Q8" indicates the card discussed earlier that computes Q8. The right half is taken up with clock and timing circuits, which generate the clock signals that control the 1401.

This rack of circuitry in the IBM 1401 contains arithmetic logic (left) and timing circuitry (right).

Conclusion

This article has discussed how the 1401 adds or subtracts a single digit. The complete addition/subtraction process in the 1401 is even more complex because the 1401 handles numbers of arbitrary length; the hardware loops over each digit to process the entire numbers.[16][17]

Studying old computers such as the IBM 1401 is interesting because they use unusual, forgotten techniques such as qui-binary arithmetic. While qui-binary arithmetic seems strange at first, its error-detection properties made it useful for the IBM 1401. Old computers are also worth studying because their circuitry can be thoroughly understood. After careful examination, you can see how arithmetic, for instance, works, down to the function of individual transistors.

Thanks to the 1401 restoration team and the Computer History Museum for their assistance with this article. The IBM 1401 is regularly demonstrated at the Computer History Museum, usually on Wednesdays and Saturdays (schedule), so check it out if you're in Silicon Valley.

Notes and references

[1] Qui-binary is the opposite of bi-quinay encoding used in abacuses and old computers such as the IBM 650. In bi-quinary, the bi part is 0 or 5, and the quinary part is 0, 1, 2, 3, or 4.

[2] You might wonder why IBM didn't just use parity instead of qui-binary numbers. While parity detects bit errors, it doesn't work well for detecting errors during addition. There's no easy way to figure out what the parity should be for a sum.

[3] The IBM 1401 has hardware to multiply and divide numbers of arbitrary length. The multiplication and division operations are based on repeated addition and subtraction, so they use the qui-binary addition circuit, along with qui-binary doublers.

[4] The logic diagrams are all from the 1401 Instructional Logic Diagrams (ILD). Pages 25 and 26 show the addition and subtraction logic if you want to see the diagrams in context.

[5] The IBM 1401 performs operations on memory locations and the A and B registers provide temporary storage for digits as they are read from core memory. They are not general-purpose registers as in most microprocessors.

[6] A few more details about the console display. The "C" bit at the top of each register is the check (parity) bit used for error detection. The 1401 uses odd parity, so if an even number of bits are set, the C bit is also set. The "M" bit at the bottom is the word mark, which indicates the end of a variable-length field. The machine opcode character is zone B + zone A + 1, which indicates the letter "A".

Unlike modern computers, the 1401 uses intuitive opcodes so "A" means add, "S" means subtract, "B" means branch and so forth. (This is the actual opcode in memory, not the assembly mnemonic.) In the lower right, the mode knob is set to "Single cycle process", which allowed me to step through the instruction to get this picture. Normally this knob is set to "Run" and the console flashes frantically as instructions are executed.

[7] One surprising feature of the BCD translator is that it accepts binary inputs from 0 to 15, not just "valid" inputs 0 to 9. Input 10 is treated as 0, since the 1401 stores the digit 0 as decimal 10 in core. Values 11 through 15 are treated as 3 through 7. Thus, every binary input results in a valid (but probably unexpected) qui-binary value. As a result, the 1401 can perform addition on non-decimal characters, but the results aren't very useful.

[8] The IBM 1401 uses 9's complements since it is a decimal machine, unlike modern binary computers which use 2's complements. For example, the complement of 1 is 8, and the complement of 4 is 5. To subtract a number, the 9's complement of each digit is added (along with a carry). An example of using complements for subtration is 432 - 145. The 9's complement of 145 is 854. 432 + 854 + 1 = 1287. Discarding the top digit yields the desired result 432 - 145 = 287. Complements are explained in more detail in Wikipedia.

[9] If you trace through the AND-OR logic in the complement circuit, you can see that each pair of AND gates and and OR gate forms a multiplexer, selecting one input or the other. For example for the B1 output: if complement is 0 AND B1 is 1, the output is 1. OR, if complement is 1 AND B0 is 1, the output is 1. In other words, the output matches the B1 input if complement is 0, and matches the B0 input if complement is 1. The box labeled I in the schematic is an inverter.

[10] The quinary adder is implemented using wired-OR logic. Instead of an explicit OR gate, the AND outputs are simply wired together to produce the OR output. While the quinary adder looks symmetrical and regular in the schematic, its implementation uses three different SMS cards: 3JMX and 4JMX AND/OR gates, and JGVW AND gates, depending on the number of AND gates feeding the output.

[11] One component of interest in the photo of SMS cards is the silver rectangle on the lower right card. This is the quartz crystal that generates timing for the 1401. The SMS card is type RK, and the crystal runs the 347.5kHz oscillator. Eight oscillator half-cycles make up the 11.5 microsecond cycle time of the 1401. At the top of the photo are the wiring bundles connecting these circuits to other parts of the computer.

[12] Due to the simplicity of the IBM 1401 compared to modern computers, it's possible to understand how the IBM 1401 works at every level all the way to quantum physics. I'll give an outline here. The gates in an SMS card use a simple form of logic called CTDL by IBM and DTL (Diode-Transistor Logic) by the rest of the world. The 3JMX card schematic shows that each input is connected through a diode to the output transistor. If any input is high, current flows through the diode and turns off the transistor. The result is an AND gate (with inverted inputs). IBM Transistor Component Circuits (page 108) explains this circuit in detail.

Going deeper, we can look inside the transistor. The board uses type 034 germanium alloy-junction transistors (details, details), very different from modern silicon-based planar transistors. These transistors consist of a germanium crystal base with indium beads fused on either side to form the emitter and collector. The regions of germanium-indium alloy form the "P" regions. In the photo, the germanium disk is in the small circular hole. Copper wires are connected to the indium beads. The photo below shows an IBM 083 transistor from the IBM 1401. This is the NPN version of the transistors in the 3JMX card. If you want a deeper understanding, look at bipolar junction transistor theory, which in turn is explained by quantum physics and solid-state device theory.

Inside a germanium alloy-junction transistor used in the IBM 1401 computer. This is an IBM 083 NPN transistor. Photo from IBM 1401 restoration team.

[13] You may wonder how 8=4+4 gets computed, since the card described doesn't handle that. The sum 4+4 is computed by the card just below the asterisk (a triple AND gate card of type JGVW). The other two AND gates in that card compute 6+6 and 8+8. To determine what each board in the IBM 1401 does, look at the Automated Logic Diagrams, page 34.32.14.2.

[14] The qui-binary carry logic happens in several phases. The qui parts are added, generating a carry if needed. The binary parts are added with a simple binary adder (not shown). A carry from the binary part shifts the qui part by 2. A carry out signal is also generated as needed. For instance, adding 3 + 5 is done by adding Q2 B1 + Q4 B1. This generates Q6 + B0 + B carry. The B carry increments the qui component to Q8, yielding the result Q8 B0 (i.e. 8).

The qui-binary to BCD translation circuit uses straightforward AND-OR logic, detecting the various combinations. Note that 0 is represented in the 1401 as binary 1010 (because binary 0000 indicates a blank), so the BCD output bits 8 and 2 are set for qui-binary value Q0 B0. The parity output is generate by combining the binary parity (even for B0; odd for B1) with the qui parity value. The qui even parity signal is set for Q0 or Q6, while the qui odd parity signal is set for Q2, Q4, Q8. Note that representing 0 as binary 1010 instead of 0000 doesn't affect the parity.

The error detection circuit uses AND-OR logic to detect bad qui-binary results. It detects a fault if no B bits are set or both B bits are set. Instead of testing every qui bit combination, it implements a short cut from the qui parity circuit. If the even qui parity signal and the odd qui parity signal are both set, this indicates multiple qui lines are set, triggering a fault. If neither qui parity signal is set, then no qui lines are set, also triggering a fault. The parity check misses a few qui combinations (such as Q0 and Q6 set), so these are tested separately. The result is that any invalid qui-binary result triggers a fault.

[15] The rack of cards shown is officially known as gate 01B3. The functions assigned to each card in the photo are approximate, because some cards are used by multiple functions. For exact information, see the plug list, which specifies the card type and function for every card in the 1401.

[16] One complication with the 1401's arithmetic instructions are numbers are stored as a positive value with a sign bit (on the last digit). This format makes printing of positive and negative numbers simpler, which is important for a business computer, but it makes arithmetic more complicated. First, the signs must be checked to determine if the numbers are being added or subtracted. Next, each digit is added or subtracted in sequence until the end of the number is reached. If the result is negative, the 1401 flips the result sign and converts the answer back to a positive value by making two additional digit-by-digit passes over the number. Modern computers use binary and handle negative numbers with two's complement, which makes subtraction much simpler. It takes 9 pages of documentation to explain the addition operation, complete with multiple flowcharts: see IBM 1401 Data Flow pages 24-32. (Keep in mind that these flowcharts are implemented in hardware, not with microcode or subroutines.)

[17] Arithmetic on the 1401 and the qui-binary adder are discussed in detail in 1401 Instruction Logic, pages 49-67. For the history leading up to qui-binary arithmetic, see this article by Carl Claunch.

Fixing the core memory in a vintage IBM 1401 mainframe

I recently had the chance to help fix one of the vintage IBM 1401 computer systems at the Computer History Museum when its core memory started acting up. As you might imagine, keeping old mainframes running is a difficult task. Most of the IBM 1401 restoration and repairs are done by a team of retired IBM engineers. But after I studied the 1401's core memory system in detail, they asked if I wanted to take a look at a puzzling memory problem: some addresses ending in 2, 4 or 6 had started failing.

An IBM 1401 mainframe computer at the Computer History Museum. Behind it to the left is the IBM 1406 Storage Unit, providing an additional 12,000 characters of storage. IBM 729 tape drives are at the right and an IBM 1402 Card Read Punch is at the far left.

The IBM 1401 was low-end business computer that became the most popular computer of the early 1960s due to its low cost: $2500 a month, Like most computers of its era it uses ferrite core memory, which stores bits on tiny magnetized rings. The photo below shows a closeup of the ferrite cores, strung on red wires.

Closeup of the core memory in the IBM 1401 mainframe, showing the tiny ferrite cores.

The 1401 had only 4,000 characters of storage internally, but could hold 16,000 characters with the addition of the IBM 1406 Storage Unit. This core memory expansion unit was about the size of a dishwasher and was connected to the 1401 computer by two thick cables.[1] This 12,000 character expansion box could be leased for $1575 a month or purchased for $55,100. (In comparison, a new house in San Francisco was about $27,000 at the time.) The failing memory locations were all in the same 4K block in the IBM 1406, which helped narrow down the problem.

A view inside the IBM 1406 Storage Unit, which provides 12,000 characters of storage for the IBM 1401 mainframe. At the left is the 8,000 character core module below the cards that control it.

The 1406 contains two separate core memory modules: one with 8,000 characters and one with 4,000 characters. In the picture above, the 8K core module is visible on the left, while the 4K core module is out of sight at the back right. Associated with each core module is circuitry to decode addresses, drive the core module, and amplify signals from the module; these circuits are in three rows of cards above each module. The 1406 also provided an additional machine opcode (Modify Address) for handling extended addresses. Surprisingly, the logic for this new opcode is implemented in the external 1406 box (the cards on the right), not in the 1401 computer itself. The 1406 box also contains hardware to dump the entire contents of memory to the line printer, performing a core dump.

The circuits in the 1406 (and the 1401) are made up of Standardized Module System (SMS) cards. A typical card has a few transistors and implements a logic gate or two. Unlike modern transistors, these transistors are made from germanium, not silicon. The photo below shows rows of SMS cards inside the 1406. Note the metal heat sinks on the high-current transistors driving the core module.

A closeup of SMS cards inside an IBM 1406 Storage Unit. The top cards have heat sinks on high-current driver transistors.

The core memory is made from planes of 4,000 cores, as seen below. Each plane is built from a grid of 50 by 80 wires, with cores where the wires cross. By simultaneously energizing one of the 50 horizontal (X) wires and one of the 80 vertical (Y) wires, the core at the intersection of the two wires is selected. Each plane holds one bit of each character, so 8 planes are stacked to hold a full character.

Core memory in the IBM 1401 mainframe. Each layer (plane) has 4,000 tiny cores in an 80x50 grid. Multiple planes are stacked to form the memory.

The photo below shows the 8K memory module inside the 1406, built from a stack of 16 core planes. (Since a stack of 8 planes makes 4K, 16 planes make 8K.) Mounted on the right of the core module are the "matrix switches", which drive the X and Y select lines; my previous core memory article explains them.

The 8,000 character core memory in the IBM 1406 Storage Unit consists of 16 layers (planes) of cores wired together. The matrix switches at the right (behind plastic) drive the control lines.

The IBM 1401 is a decimal machine and it uses 3-digit decimal addresses to access memory. The obvious question is how can it access 16,000 locations with a 3-digit address. To understand that requires a look at the characters used by the IBM 1401.

The IBM 1401 predates 8-bit bytes, and it used 6-bit characters. Each character consisted of a 4-bit BCD (binary-coded decimal) digit along with two extra "zone" bits. By setting zone bits, letters and a few symbols could be stored. For instance, with both zone bits set, the BCD digit values 1 through 9 corresponded to the characters "A" through "I". Other zone bit combinations provided the rest of the alphabet. While this encoding may seem strange, it maps directly onto IBM punched cards, which have 10 rows for the digit and two rows for zone punches. This encoding was called BCDIC (Binary-Coded Decimal Interchange Code), and later became the much-derided EBCDIC (Extended BCDIC) encoding. (You may have noticed that 8 planes are used for 6-bit characters. One extra plane holds special "word mark" bits, and the other holds parity.)

The point of this digression into IBM character encoding is that a three-digit address also included 6 zone bits. Four of these bits were used as part of the address, allowing 16,000 addresses in total.[2] For example, the address 14,578 would be represented as the digits 578 along with the appropriate zone bits, so the resulting address would be represented as the three characters "N7H".[3]

Getting back to the problem with the memory unit, the 4K bank was failing with addresses ending in 2, 4 and 6. Looking at 2, 4 and 6, I immediately concluded that what these all had in common was the 2 bit was set. Except 4 doesn't have the 2 bit set. So maybe the problem was with even addresses. Except 0 and 8 worked. After staring at bit patterns a while, I became puzzled because 2, 4 and 6 didn't really have anything in common.

Looking at the logic diagrams reveals the hardware optimization that makes 2, 4, and 6 have something in common. Since the problem happened with specific unit digits, the problem was most likely in the address decoding circuitry that translates the unit digit to a particular select line.[4] The normal way of decoding a digit is to look at the 4 bits of the digit to determine the value. Unexpectedly, the decoder only looks at 3 bits; this reduces the hardware required, saving money. For instance, the digit 2 is detected below if the 4 bit is clear, the 1 bit is clear, and the 8 bit is clear. The digit 4 is detected if the parity (CD) bit is clear, the 4 bit is set, and the 1 bit is clear. The digit 6 is detected if the 1 bit is clear, the 2 bit is set, and the 4 bit is set.[5] Looking at the decode logic, decoding of the digits 2, 4, and 6 (and only these digits) tests that the 1 bit is clear. Now the failure starts to make sense. If something is wrong with the units 1-bit-clear signal, these digits would not be decoded properly and memory would fail in the way observed.

The Instructional Logic Diagrams (ILD) for the IBM 1401 explain the circuitry of the computer. The above diagram shows part of the address decode logic used for the core memory.

The next step was to figure out how the units 1-bit-clear signal could be wrong. You'd expect a failure of one address bit to be catastrophic, not just limited to one memory bank. Looking at the specifics of the decoder circuitry revealed the problem.

Every connection and circuit of the IBM 1401 is documented in an Automated Logic Diagram (ALD). These diagrams were generated by computer and put in a set of binders for use by service engineers. The code number 42.73.11.2 on the previous diagram provides the page number of the related ALD. While these diagrams are extremely detailed, they are nearly incomprehensible. Since I'm using copies of reduced 50-year-old line printer output, the ALDs are also barely readable.

The Automated Logic Diagrams (ALD) for the IBM 1401 mainframe computer consist of hundreds of pages that show every card and connection in the computer. The above diagram shows part of the address decode circuitry in the IBM 1406 Storage Unit.

The diagram above shows part of the ALD for the units memory address decoding. Each box corresponds to a logic component on an SMS card and the lines show the wiring between cards. At the bottom of each box, "AEM-" indicates the type of SMS card. The reference information for an AEM/AQU card reveals that it is a Switch Decode card with two circuits. Each circuit combines an inverter, a three-input AND gate, and a high-current driver.[6]

Now we can see the root cause of the problem. The unit address bit 1 (highlighted in red on the ALD) goes into pin A of the Units 4 card and is inverted. The inverted value (pin D, yellow) then goes to the Units 2 and Units 6 cards, generating the decode outputs (green). If something is wrong with this signal, addresses 2, 4, and 6 won't decode, which is exactly the problem encountered. Thus, the Units 4 card seemed like the problem.

This IBM Standard Modular System (SMS) card is used by the core memory to decode addresses. It has two high-current outputs, driven by the germanium transistors at the top with red heat sinks. The card type "AEM" is stamped into the bottom left of the card.

The diagram above indicates that the Units 4 card is card E15 in rack 06B5, which is in the right rear of the 1406 unit.[7] Once I'd located the right rack, I needed to find card E15. The three rows of cards are D through F (top). I counted to position 15 of 26 in row E. The photo below shows the position of the card (red arrow).

Circuitry inside the IBM 1406 Storage Unit. The green arrow indicates the 4,000 character core memory. The cards above it control the memory. The top row of cards has high-current drivers for the memory. The cards in the middle row decode addresses. The bottom row contains amplifiers to read the signals from the memory. The red arrow indicates the position of the faulty card. The fan above the cards provides cooling airflow. At the right, colorful wire bundles connect the circuitry.

One convenient thing about the IBM 1401 and its peripherals is they are designed for easy maintenance. In many cases, you don't even need any tools. To get inside the IBM 1406, you just pop the front or side panels off (as shown below). The SMS cards have a metal cover to guide the cooling airflow, but that just pops off too. It's easy to attach an oscilloscope to see what's happening, although I didn't need to do that. The SMS cards themselves are easily pulled from their sockets. I'm told you don't even need to power down the system to replace cards, but of course I turned off the power.

Inside the IBM 1406 Storage Unit. At the left are the power supplies, including a 450W ferro-resonant regulator. The 8K core memory is at the right, connected by yellow wire bundles to the control circuitry above.

I pulled out the card in slot E15, plugged in a replacement card from the 1401 lab's collection, and powered up the system. Much to my surprise, the memory worked perfectly after replacing the card. Some of the engineers (Stan, Marc, and Dave) tested the transistors on the bad card but didn't find any problems. After cleaning the bad card and swapping it back, the memory still worked, so there must have been some dirt or corrosion making a bad connection. They say this is the first problem they've seen due to bad connections, so the thick gold plating on the SMS card contacts must work well.

Conclusion

It's not every day one gets the chance to help fix a 50 year old mainframe, so it was an interesting experience. I was lucky that this problem turned out to be easy to resolve. The guys repairing the tape drives and card reader have much harder problems, since those devices are full of mechanical parts that haven't aged well.

Thanks to the members of the 1401 restoration team and the Computer History Museum for their assistance. Special thanks to Stan Paddock, Marc Verdiell and Dave Lion for inviting me to investigate this problem.

The IBM 1401 is demonstrated at the Computer History Museum on Wednesdays and Saturdays (unless there is a hardware problem) so check it out if you're in Silicon Valley (schedule).

Notes and references

[1] The 1406 expansion unit was 29" wide, 30 5/8" deep and 39 5/8" high and weighed 350 lbs. The 10 foot cables between the 1401 computer and the 1406 storage unit are each 1 1/4" thick; one provides power and the other has signals. The 1406 generates 250 watts of heat, which is less than I would have expected. Details are in the installation manual.

[2] The three-digit address has six zone bits in total. Four are used as part of the address. The other two zone bits to indicate an indexed address using one of three index registers (which are actually part of core, not separate registers). Indexed addressing was part of the "Advanced Programming" option which cost an extra $105 per month.

[3] For full information on converting addresses to characters, see the IBM 1401 Pocket Reference Manual, page 3.

[4] Scans of the Instructional Logic Diagrams (ILDs) are available online. The memory decode circuits are on page 56. Scans of the Automated Logic Diagrams (ALDs) are also available online; the core memory is in section 42.

[5] The IBM 1401 predates standardized logic symbols, so the logic diagram symbols may be confusing: the triangular symbol is an AND gate. The SWD (Switch Decode) card inverts its inputs, but that isn't shown on the logic diagram.

There are few subtleties in the decoding logic. You might think that the circuit described would decode a 0 digit as a 2 digit since the 1, 4, and 8 bits are clear. However, the IBM 1401 stores the digit 0 as the value 10 (8 bit and 2 bit set), since a blank is stored with all bits clear.

For the decoding using the parity bit, note that the IBM 1401 uses odd parity. For instance, the digit 4 (binary 0100) already has odd parity, so the CD (check digit) parity bit is clear. The digit 5 (binary 0101) has the CD parity bit set so three bits are set in total.

[6] The original idea of SMS cards was to build computers from a small set of standardized cards, but as you can guess from the complexity of the AEM card, engineers created highly-specialized SMS cards for specific purposes. IBM ended up with thousands of different SMS card types, defeating the advantages of standardization. I've created an SMS card database that describes a thousand different SMS cards.

[7] The 06B5 designation indicates which gate holds the card. (Each rack of cards is called a "gate" in IBM terminology. Confusingly, this has nothing to do with a logic gate.) The 06 indicates the 1406 frame. The B indicates a lower frame. Position 5 is in the back right. The same numbering system is used in the IBM 1401 itself. The 1401 is built around the same frame structure as the 1406, except with four frames, stacked 2x2. The left frames are numbered 01, and the right frames are 02. The frames on top are A, and the frames on the bottom are B. Gates 1 through 4 are in the front, and 5 through 8 continue around the back. A typical 1401 gate identifier is "01B2", which indicates the rack on the front of the 1401 below the console. (The use of frames to build computers and peripherals led to the term "main frame" to describe the processing unit itself.)

Examining the core memory module inside a vintage IBM 1401 mainframe

The IBM 1401 mainframe computer was announced in 1959 and by the mid-1960s had become the best-selling computer, extremely popular with medium and large businesses because of its low cost. A key component of the 1401's success was its 4,000 character core memory, which stored data on tiny magnetized rings called cores.

The 4000-character core memory module from the IBM 1401 mainframe.

The core module is surprisingly complex, as can be seen above, with thousands of tiny cores mounted on red wires. The module consists of 16 frames stacked together and requires a large amount of wiring. The remainder of the article will dive into the details of this core module. (For an overview of the 1401, see my articles about Bitcoin mining and fractals on the 1401.)

The IBM 1401 mainframe from the 1960s. The 1403 line printer is to the right, and a 792 tape drive at the back.

The IBM 1401 mainframe (above) is about the size of two refrigerators. The core memory module in the 1401 can be accessed by swinging open the computer's front panel, as seen below. The console switches, lights, and wiring are on the left. The core module itself is in the center, mostly hidden behind the brown circuit board.

Opening the console panel (left) of the IBM 1401 mainframe shows the 4K core memory unit (center).

The diagram below illustrates how the character 'A' is stored in core memory. Each bit of data in memory is stored in a tiny ferrite ring or core. These cores can be magnetized in one of two directions, corresponding to a 0 or 1 bit. The cores are arranged into a grid of 4000 cores, called a plane. To select an address, an X wire and a Y wire are activated, selecting the cores where those two wires cross. Each plane stores one bit and planes are stacked up to store a character. You might expect 8 planes are used to store a byte, but the IBM 1401 predates bytes; it uses 6-bit characters based on BCD (binary-coded decimal). Each location also has a special metadata bit called the "word mark", indicating the start of a field or instruction. Adding the parity bit yields eight bits of storage at each address.

Diagram from the 1401 Reference Manual representing how the character 'A' is stored in core memory.

Because the IBM 1401 was a business computer, it uses decimal arithmetic rather than binary arithmetic; each character is a binary-coded decimal value, along with two extra "zone bits" for alphanumeric characters. Since the 1401 uses three-character addresses, you might expect that it could only access 1000 locations. The trick is the two zone bits of the hundreds character provided the thousands digit 0 to 3. A consequence is that addresses above 1000 turn into alphanumerics instead of digits; location 2345 is addressed as L45.

Properties of ferrite cores

The physical properties of ferrite cores are critical to the operation of the core memory, so it is important to understand them. First, if a wire through a core carries a strong current, the core will be magnetized according to the direction of the current (following the right-hand rule). Current in one direction will write a 1 to the core, while the opposite current will cause the opposite magnetization and write a 0 to the core.

Hysteresis is a key property of the cores: current must exceed a threshold to affect a core's magnetization. A small current will have no effect on the core, but a current above a threshold will cause the core to "snap" into the magnetized state aligned with the current.

Closeup of the ferrite cores from the IBM 1401 mainframe's 4K storage. Four wires run through each core: X select, inhibit, Y select, and sense.

The hysteresis property makes it possible to select a particular core. A "half-write" current is sent through the appropriate X select wire and a "half-write" current through the Y select wire. The single core with the selected X and Y wires will have enough current to change state, but the other cores will not have enough current, and will remain unchanged.

The final important property is that when a core switches its direction of magnetization, it induces a current in a sense wire through the core (kind of like a transformer). If the core already has the target state and doesn't change magnetization, no current is induced. This induced current is used to read the state of a core. A consequence is that reading a core erases it, and the desired value must be written back to the core.

Structure of a core plane

Each core plane has 4000 cores arranged as a 50x80 grid of cores. (The I/O planes are configured differently, and will be explained later.) To reduce interference, the ferrite cores are arranged in a "checkerboard" pattern with each core arranged diagonally in the opposite direction from its neighbors. Four wires pass through each core. The horizontal wires are the X select line and the inhibit line (used for writing). The vertical wires are the Y select line and the sense line (used for reading). The X and Y select lines go through all the planes, so all planes are accessed in parallel.

Core memory in the IBM 1401. Each plane of cores has 4000 cores in a 80x50 grid.

To read a core, the X and Y select lines magnetize the selected cores to the "0" direction. If the core was previously in the "1" state, the core's state change induces a current in the sense wire. If the core was already in the "0" state, no current is induced. Thus, the sense wire allows the bit stored in the core to be determined. The read process destroys the previous value of the core, leaving it in the 0 state. Each plane has a sense wire threaded through all the cores in the plane.

To write a core, current of the opposite polarity is sent through the X and Y select lines to magnetize the core into the 1 state. To keep the core in the 0 state, a current is sent through the plane's inhibit line. The inhibit wire runs through all the cores in a plane parallel to the X select lines. By running the reverse current through the inhibit wire, the X line's current is canceled out, and the core remains unchanged. The inhibit current is too low to flip a core by itself, so other cores are not zeroed out.

The diagram below shows the reverse-engineered wiring topology of an IBM 1401 core memory plane. Most of the core has been cut out of the diagram, as indicated by the dotted gray lines. The sides of the plane are labeled A through D, matching the 1401 documentation. The A and C sides have 56 pins, while the B and D sides of the plane have 104 pins. Not all the pins are connected.

The wiring topology of the IBM 1401's core memory plane.

The X select lines are in green and the Y select lines are in red. The select lines are generated in a complex way by matrix switches, so core addresses are not arranged sequentially. Each matrix switch takes two sets of input lines and activates an output line based on the input values. The 5x10 X matrix switch has 5 row inputs and 10 column inputs, producing 50 outputs, which are the X select lines. The 10 column inputs come from the units digit, and the 5 row inputs are the "even hundreds" digit. The 8x10 Y matrix switch has 8 row inputs and 10 column inputs, producing 80 outputs for the Y select lines. The 10 column inputs are from the tens digit and the 8 row inputs are a tricky combination of the thousands and "odd hundreds". This scheme may seem overly complicated, but it minimizes the hardware required for address decoding.

Each half of the core plane (0-1999 and 2000-3999) has a separate sense line loop, but they are usually wired together. The two sense lines are in blue and run in the Y direction. The sense lines are carefully arranged to avoid picking up interference. The lines cross over along the midpoint to cancel out noise from the Y select lines - the sense line runs in the opposite direction along half of each Y select line, so any induced signal will be canceled out. In addition, the sense lines are twisted as they exit the middle of the plane, to avoid picking up interference. (Many other core memory systems avoid interference by running the sense line diagonally, but the 1401 uses a rectangular layout.)

Each half of the plane has a separate inhibit line. The two inhibit lines are in brown and run next to the X select lines, which they inhibit. The two lines are normally driven separately to reduce noise, but have the same signal. Since the inhibit line switches direction each row, alternating X select lines are also driven in opposite directions.

The card reader/punch, the printer, and the I/O cores

One unusual feature of the core module is the eight special-purpose I/O frames: six core planes and two terminal frames. To understand the I/O cores, some background on the IBM 1401 is necessary. The 1401 was used in business applications such as accounting and payroll, so accuracy was extremely important. If a malfunction caused bad payroll checks to be printed, it would be a catastrophe. To catch problems, IBM put many types of validity checking into the 1401, making it much more reliable than competitors. The basic I/O devices for the 1401 were the card reader/punch and the line printer, separate units from the computer itself and the I/O cores detected problems with these devices.

The I/O planes are addressed exactly the same as the data planes. However, the I/O planes are very sparse, with only 297 cores rather than 4000 cores, so most locations have no storage as can be seen in the photo below. These planes are accessed by the I/O circuitry, and are invisible to the programmer.

Closeup of the IBM 1401's core memory. The row bit core planes are used for I/O and are sparsely populated.

The IBM 1401 uses 80-character punch cards. You might expect the card reader to read each character on the card in sequence and send the character to the computer, but that's not at all how it works. Instead, the card reader processes each card "sideways" for speed, using 80 metal brushes to read a row at a time. If a card has a hole in a position, the brush contacts a metal roller under the card, completing a circuit. The brushes are connected to the IBM 1401 by 80 wires, one for each brush. Each wire is connected directly to a "row-bit core" in the core memory module, setting the core if a hole was detected. There's no driver circuitry or memory addressing; it's literally a separate wire from each brush that is wrapped 5 times around a core. Let me emphasize how unusual this is: it's like having a separate wire from each key on your keyboard directly to a specific transistor in your memory chip.

The card reader/punch has three read stations: RD1 and RD2 for reading, and PCH for reading after punching. Since each read station has 80 brushes, 240 wires connect the brushes to the 240 row-bit cores. (As you might have guessed, the cables between the 1401 computer and the reader/punch are very thick.) As well as the row-bit cores, reading/punching uses core planes called XU, YU, XL, and YL to count the number of holes detected in each position. If the two read stations have different hole counts, the computer stops and reports a fault. Likewise, the count is checked after punching a card to make sure all holes were punched correctly.

The high-speed line printer uses 132 hammers to produce 132-column output. A chain with the 48 printable characters whizzes around horizontally. As each character on the chain passes a position where it should be printed, a hammer fires at the precise time, hitting the paper against the inked ribbon to print the character. The I/O cores are also used to detect problems in the printing process.

Printing uses several different core planes for multiple validity checks. Each of the 132 print hammers is wired directly to a "hammer-fire core" in the memory module. The XU core plane is used during printing for the print-compare check: a bit is set in the XU plane if a hammer should fire for the character position. These 132 bits are compared with the hammer-fire cores to verify that the correct hammers fired. Plane YL holds print-line complete cores that verify that every character position either printed a character or holds a non-printable character. Finally, to aid printer maintenance, plane YU records the location of any fault in print-error storage core.

Physical layout of the core module

The core module consists of 16 frames in a stack - 14 core planes and two terminal frames. The upper 8 frames hold the character data planes and the lower 8 frames are the I/O frames. The following table shows the usage of each frame. The terminal frames do not contain cores, but provide connections for the large wire bundles from the reader brushes and the print hammers.

1:	Bit 8
2:	Bit 4
3:	Bit 2
4:	Bit 1
5:	Bit A
6:	Bit B
7:	Parity
8:	Word Mark
9:	Terminals for frame 10
10:	Card reader brushes (RD2), punch brushes (PCH)
11:	Terminals for frame 12
12:	Card reader brushes (RD1), print hammers (PRT)
13:	XU (I/O)
14:	YU (I/O)
15:	XL (I/O)
16:	YL (I/O)

The picture below shows the large amount of wiring required by the core module. Frame 16 (YL) is at the left and frame 1 (bit 8) is at the right. The two matrix switches are on the front of the module: the 8x10 switch for the Y select lines is at top, and the 5x10 switch for the X select lines is at the bottom.

The core memory module from the IBM 1401 mainframe.

The yellow wires at the left and right connect the Y select lines on frame 16 and frame 1 to the 8x10 matrix switch. Two bundles of wires connect to I/O planes near the middle of the module. One connects the brushes in the card reader and the printer hammer drivers to terminals on frame 11. The other bundle connects read brushes and punch check brushes to terminals on frame 9. The horizontal wire bundle across the middle of the planes connects the inhibit lines of each plane.

The photo below provides another view, focusing on the data plane wiring. At front is frame 1, the core plane for data bit 8, with the gray cores visible on red wires. The other 15 frames are layered behind frame 1. The two matrix switches are on top. The 8x10 matrix switch is connected to the Y select lines on the top and the 5x10 matrix switch is connected to the X select lines on the left.

The core memory module from the IBM 1401 mainframe. The cores in one of the planes are visible, strung along red wires. At the top, two matrix decoder boards generate the 50 X select lines and 80 Y select lines, addressing one of 4000 storage locations. The X select lines are connected to the core planes by the yellow wires on the left side of the core module, while the Y select lines are connected on top.

The detailed block diagram below shows how the components are connected in the 1401's core memory system. This diagram shows the physical arrangement of the 16 frames in the core memory module, along with the driver circuitry. The inhibit drivers are at the upper left, feeding each core plane. The sense amplifiers are at the upper right. The 5x10 X matrix switch is in the lower left, and the 8x10 Y matrix switch is in the lower right. Note the read brushes, punch brushes, and print hammer drivers are wired directly into the core module through the terminal frames. The diagram also shows the timing of the read and write pulses, and how they have opposite polarity, writing 0 and 1 respectively.

Diagram of the core memory system in the IBM 1401 mainframe from ALD 42.41.11.2.

The matrix switches

Generating the X and Y select signals is a tricky problem. The drive signals must have a positive pulse of the right current and duration for reading, followed by a negative pulse for writing. In addition, the number of select lines is large (50 X and 80 Y), so hardware costs would be excessive if each line had its own driver circuitry.

The 1401 uses an interesting solution to drive the select signals. Matrix switches generate the select signals by using a set of ferrite cores. But instead of storage, these cores are used for their switching properties. As with storage, the matrix switch depends on the "coincident current" property, where two signals of sufficient current will cause a core to snap to the opposite magnetization. But instead of being used for storage, the cores in the matrix switch generate a drive signal.

The 5x10 matrix switch in the IBM 1401 mainframe. This board provides the drive signals for the core module.

The photo above shows the X matrix switch. The switch consists of 50 cores in a 5 by 10 grid, with 5 lines driving the rows and 10 lines driving the columns. Each core also has an output winding and a bias winding. When two input lines are triggered, the corresponding core flips state, generating a pulse on the output winding. When the input lines are released, the bias winding flips the core back to its original state, generating a negative pulse on the output winding. Thus, the desired one of the 50 outputs has a positive pulse followed by a negative pulse, which is just what the core module requires for read followed by write.

The photo below shows the wiring of the matrix switch cores. The bias wire (black) is wound through pairs of cores three times. Each horizontal input wire (red) is wound through pairs of cores about twelve times, as are the vertical input wires. Each core has an output wire wound diagonally about twelve times.

Closeup of the matrix switch used in the IBM core memory. Each ferrite ring drives one of the select lines in the core memory.

How core memory is mounted in the 1401

The following picture shows the core memory module mounted in its rack, along with the many SMS cards required by the core module. (IBM built computers from Standard Modular System cards, each about the size of a playing card and holding a few transistors and other components.) At the left are the driver cards and current source cards that drive the matrix switch boards, and the driver cards for the inhibit lines. The next column holds the address decode cards. The address lines plug into the empty sockets at the bottom. The next column holds the sense line pre-amplifier and amplifier cards. The core module itself is mounted with the matrix switch cards on top. At the far right are the sockets for the hundreds of wires from the brushes and print hammers.

Core memory module and associated circuit board from an IBM 1401 mainframe. Photo courtesy of Rob Storey.

The photo below shows the core module mounted inside the IBM 1401 mainframe, looking into the left end of the computer. The core module is behind the bundle of black and yellow wires, mostly address lines. The matrix switches are on the left. The colorful brush and hammer wires are connected via paddles underneath the core module. The SMS driver cards are above the core module, mostly behind a metal cover for airflow.

The core memory module inside the IBM 1401 mainframe. The module is in the lower right, with the driver cards above

The photo shows some other interesting features of the 1401. At the top of the computer is the time meter that records how much time the computer has been running. IBM usually leased the 1401 and if you used the computer more than 8 hours per day, they would charge you for the excess. (Unless, of course, you paid for the 24/7 lease.) In the upper right is the "convenience" outlet located inside the computer, a standard electrical outlet. Below the outlet is the wiring on the back of the front console. The computer didn't use a backplane; instead, many loose bundles of wires connected circuitry modules, as you can see at the bottom of the photo.

Conclusion

Core memory was the leading memory technology from the mid-1950s until it was replaced by semiconductor memory in the early 1970s. For its time, core memory provided dense, reliable, and inexpensive storage, but memory technology has improved incredibly since then. The 1401 had a 11.5 microsecond memory cycle time, compared to 5 nanoseconds for modern RAM. While the 1401 had 4000 characters of storage (expandable to 16K), modern computers have many gigabytes. Adding a 4K memory expansion to the 1401 cost $20,100 ($162,000 in current dollars). Now a 16 gigabyte memory costs under $100. But even though it is obsolete, core memory is still an interesting technology to examine.

Thanks to the members of the 1401 restoration team and the Computer History Museum for their assistance The IBM 1401 is demonstrated at the Computer History Museum on Wednesdays and Saturdays (subject to hardware problems) so check it out if you're in Silicon Valley (schedule).

References

The IBM 1401 core module is documented in detail in 1401 ALD 42 and 1401 Instructional Logic Diagrams. For more information on core memory, see Coincident Current Ferrite Core Memories and Magnetic Core Memory Systems.

Bitcoin mining on a 55 year old IBM 1401 mainframe: 80 seconds per hash

Could an IBM mainframe from the 1960s mine Bitcoin? The idea seemed crazy, so I decided to find out. I implemented the Bitcoin hash algorithm in assembly code for the IBM 1401 and tested it on a working vintage mainframe. It turns out that this computer could mine, but so slowly it would take more than the lifetime of the universe to successfully mine a block. While modern hardware can compute billions of hashes per second, the 1401 takes 80 seconds to compute a single hash. This illustrates the improvement of computer performance in the past decades, most famously described by Moore's Law.

The photo below shows the card deck I used, along with the output of my SHA-256 hash program as printed by the line printer. (The card on the front of the deck is just for decoration; it was a huge pain to punch.) Note that the second line of output ends with a bunch of zeros; this indicates a successful hash.

Card deck used to compute SHA-256 hashes on IBM 1401 mainframe. Behind the card deck is the line printer output showing the input to the algorithm and the resulting hash.

How Bitcoin mining works

Bitcoin, a digital currency that can be transmitted across the Internet, has attracted a lot of attention lately. If you're not familiar with how it works, the Bitcoin system can be thought of as a ledger that keeps track of who owns which bitcoins, and allows them to be transferred from one person to another. The interesting thing about Bitcoin is there's no central machine or authority keeping track of things. Instead, the records are spread across thousands of machines on the Internet.

The difficult problem with a distributed system like this is how to ensure everyone agrees on the records, so everyone agrees if a transaction is valid, even in the presence of malicious users and slow networks. The solution in Bitcoin is a process called mining—about every 10 minutes a block of outstanding transactions is mined, which makes the block official.

To prevent anyone from controlling which transactions are mined, the mining process is very difficult and competitive. In particular a key idea of Bitcoin is that mining is made very, very difficult, a technique called proof-of-work. It takes an insanely huge amount of computational effort to mine a block, but once a block has been mined, it is easy for peers on the network to verify that a block has been successfully mined. The difficulty of mining keeps anyone from maliciously taking over Bitcoin, and the ease of checking that a block has been mined lets users know which transactions are official.

As a side-effect, mining adds new bitcoins to the system. For each block mined, miners currently get 25 new bitcoins (currently worth about $6,000), which encourages miners to do the hard work of mining blocks. With the possibility of receiving $6,000 every 10 minutes, there is a lot of money in mining and people invest huge sums in mining hardware.

Line printer and IBM 1401 mainframe at the Computer History Museum. This is the computer I used to run my program. The console is in the upper left. Each of the dark rectangular panels on the computer is a "gate" that can be folded out for maintenance.

Mining requires a task that is very difficult to perform, but easy to verify. Bitcoin mining uses cryptography, with a hash function called double SHA-256. A hash takes a chunk of data as input and shrinks it down into a smaller hash value (in this case 256 bits). With a cryptographic hash, there's no way to get a hash value you want without trying a whole lot of inputs. But once you find an input that gives the value you want, it's easy for anyone to verify the hash. Thus, cryptographic hashing becomes a good way to implement the Bitcoin "proof-of-work".

In more detail, to mine a block, you first collect the new transactions into a block. Then you hash the block to form an (effectively random) block hash value. If the hash starts with 16 zeros, the block is successfully mined and is sent into the Bitcoin network. Most of the time the hash isn't successful, so you modify the block slightly and try again, over and over billions of times. About every 10 minutes someone will successfully mine a block, and the process starts over. It's kind of like a lottery, where miners keep trying until someone "wins". It's hard to visualize just how difficult the hashing process is: finding a valid hash is less likely than finding a single grain of sand out of all the sand on Earth. To find these hashes, miners have datacenters full of specialized hardware to do this mining.

I've simplified a lot of details. For in-depth information on Bitcoin and mining, see my articles Bitcoins the hard way and Bitcoin mining the hard way.

The SHA-256 hash algorithm used by Bitcoin

Next, I'll discuss the hash function used in Bitcoin, which is based on a standard cryptographic hash function called SHA-256. Bitcoin uses "double SHA-256" which simply applies the SHA-256 function twice. The SHA-256 algorithm is so simple you can literally do it by hand, but it manages to scramble the data entirely unpredictably. The algorithm takes input blocks of 64 bytes, combines the data cryptographically, and generates a 256-bit (32 byte) output. The algorithm uses a simple round and repeats it 64 times. The diagram below shows one round, which takes eight 4-byte inputs, A through H, performs a few operations, and generates new values for A through H.

SHA-256 round, from Wikipedia created by kockmeyer, CC BY-SA 3.0.

The dark blue boxes mix up the values in non-linear ways that are hard to analyze cryptographically. (If you could figure out a mathematical shortcut to generate successful hashes, you could take over Bitcoin mining.) The Ch "choose" box chooses bits from F or G, based on the value of input E. The Σ "sum" boxes rotate the bits of A (or E) to form three rotated versions, and then sums them together modulo 2. The Ma "majority" box looks at the bits in each position of A, B, and C, and selects 0 or 1, whichever value is in the majority. The red boxes perform 32-bit addition, generating new values for A and E. The input W_t is based on the input data, slightly processed. (This is where the input block gets fed into the algorithm.) The input K_t is a constant defined for each round.

As can be seen from the diagram above, only A and E are changed in a round. The other values pass through unchanged, with the old A value becoming the new B value, the old B value becoming the new C value and so forth. Although each round of SHA-256 doesn't change the data much, after 64 rounds the input data will be completely scrambled, generating the unpredictable hash output.

The IBM 1401

I decided to implement this algorithm on the IBM 1401 mainframe. This computer was announced in 1959, and went on to become the best-selling computer of the mid-1960s, with more than 10,000 systems in use. The 1401 wasn't a very powerful computer even for 1960, but since it leased for the low price of $2500 a month, it made computing possible for mid-sized businesses that previously couldn't have afforded a computer.

The IBM 1401 didn't use silicon chips. In fact it didn't even use silicon. Its transistors were built out of a semiconductor called germanium, which was used before silicon took over. The transistors and other components were mounted on boards the size of playing cards called SMS cards. The computer used thousands of these cards, which were installed in racks called "gates". The IBM 1401 had a couple dozen of these gates, which folded out of the computer for maintenance. Below, one of the gates is opened up showing the circuit boards and cabling.

This shows a rack (called a "gate") folded out of the IBM 1401 mainframe. The photo shows the SMS cards used to implement the circuits. This specific rack controls the tape drives.

Internally, the computer was very different from modern computers. It didn't use 8-bit bytes, but 6-bit characters based on binary coded decimal (BCD). Since it was a business machine, the computer used decimal arithmetic instead of binary arithmetic and each character of storage held a digit, 0 through 9. The computer came with 4000 characters of storage in magnetic core memory; a dishwasher-sized memory expansion box provided 12,000 more characters of storage. The computer was designed to use punched cards as input, with a card reader that read the program and data. Output was printed on a fast line printer or could be punched on more cards.

The Computer History Museum in Mountain View has two working IBM 1401 mainframes. I used one of them to run the SHA-256 hash code. For more information on the IBM 1401, see my article Fractals on the IBM 1401.

Implementing SHA-256 on the IBM 1401

The IBM 1401 is almost the worst machine you could pick to implement the SHA-256 hash algorithm. The algorithm is designed to be implemented efficiently on machines that can do bit operations on 32-bit words. Unfortunately, the IBM 1401 doesn't have 32-bit words or even bytes. It uses 6-bit characters and doesn't provide bit operations. It doesn't even handle binary arithmetic, using decimal arithmetic instead. Thus, implementing the algorithm on the 1401 is slow and inconvenient.

I ended up using one character per bit. A 32-bit value is stored as 32 characters, either "0" or "1". My code has to perform the bit operations and additions character-by-character, basically checking each character and deciding what to do with it. As you might expect, the resulting code is very slow.

The assembly code I wrote is below. The comments should give you a rough idea of how the code works. Near the end of the code, you can see the table of constants required by the SHA-256 algorithm, specified in hex. Since the 1401 doesn't support hex, I had to write my own routines to convert between hex and binary. I won't try to explain IBM 1401 assembly code here, except to point out that it is very different from modern computers. It doesn't even have subroutine calls and returns. Operations happen on memory, as there aren't any general-purpose registers.

               job  bitcoin
     * SHA-256 hash
     * Ken Shirriff  //righto.com
               ctl  6641

               org  087
     X1        dcw  @000@
               org  092
     X2        dcw  @000@
               org  097
     X3        dcw  @000@
     
               org  333
     start     cs   299
               r
               sw   001
               lca  064, input0
               mcw  064, 264
               w
     * Initialize word marks on storage
               mcw  +s0, x3

     wmloop    sw   0&x3  
               ma   @032@, x3
               c    +h7+32, x3
               bu   wmloop
     
               mcw  +input-127, x3      * Put input into warr[0] to warr[15]
               mcw  +warr, x1
               mcw  @128@, tobinc
               b    tobin
     
     * Compute message schedule array w[0..63]
  
               mcw  @16@, i
     * i is word index 16-63   
     * x1 is start of warr[i-16], i.e. bit 0 (bit 0 on left, bit 31 on right)   
               mcw  +warr, x1
     wloop     c    @64@, i
               be   wloopd
     
     * Compute s0
               mcw  +s0, x2
               za   +0, 31&x2               * Zero s0
     * Add w[i-15] rightrotate 7
               sw   7&x2               * Wordmark at bit 7 (from left) of s0
               a    56&x1, 31&x2       * Right shifted: 32+31-7 = bit 24 of w[i-15], 31 = end of s0
               a    63&x1, 6&x2        * Wrapped: 32+31 = end of w[i-15], 7-1 = bit 6 of s0   
               cw   7&x2               * Clear wordmark
     * Add w[i-15] rightrotate 18
               sw   18&x2              * Wordmark at bit 18 (from left) of s0
               a    45&x1, 31&x2       * Right shifted: 32+31-18 = bit 13 of w[i-15], 31 = end of s0
               a    63&x1, 17&x2       * Wrapped: 32+31 = end of w[i-15], 18-1 = bit 17 of s0   
               cw   18&x2              * Clear wordmark
     * Add w[i-15] rightshift 3
               sw   3&x2               * Wordmark at bit 3 (from left) of s0
               a    60&x1, 31&x2       * Right shifted: 32+31-3 = bit 28 of w[i-15], 31 = end of s0
               cw   3&x2               * Clear wordmark
     * Convert sum to xor
               mcw  x1, x1tmp
               mcw  +s0+31, x1         * x1 = right end of s0
               mcw  @032@, x2          * Process 32 bits
               b    xor
               sw   s0                 * Restore wordmark cleared by xor
     
               mcw  x1tmp, x1
     
     * Compute s1         
               mcw  +s1, x2
               za   +0, 31&x2               * Zero s1
     * Add w[i-2] rightrotate 17
               sw   17&x2              * Wordmark at bit 17 (from left) of s1
               a    462&x1, 31&x2      * Right shifted: 14*32+31-17 = bit 14 of w[i-2], 31 = end of s1
               a    479&x1, 16&x2      * Wrapped: 14*32+31 = end of w[i-2], 17-1 = bit 16 of s1   
               cw   17&x2              * Clear wordmark
     * Add w[i-2] rightrotate 19
               sw   19&x2              * Wordmark at bit 19 (from left) of s1
               a    460&x1, 31&x2      * Right shifted: 14*32+31-19 = bit 12 of w[i-2], 31 = end of s1
               a    479&x1, 18&x2      * Wrapped: 14*32+31 = end of w[i-2], 19-1 = bit 18 of s1  
               cw   19&x2              * Clear wordmark
     * Add w[i-2] rightshift 10
               sw   10&x2              * Wordmark at bit 10 (from left) of s1
               a    469&x1, 31&x2      * Right shifted: 14*32+31-10 = bit 21 of w[i-2], 31 = end of s1
               cw   10&x2              * Clear wordmark
     * Convert sum to xor
               mcw  +s1+31, x1         * x1 = right end of s1
               mcw  @032@, x2          * Process 32 bits
               b    xor
               sw   s1                 * Restore wordmark cleared by xor
     
     * Compute w[i] := w[i-16] + s0 + w[i-7] + s1
               mcw  x1tmp, x1
               a    s1+31, s0+31       * Add s1 to s0
               a    31&x1, s0+31       * Add w[i-16] to s0
               a    319&x1, s0+31      * Add 9*32+31 = w[i-7] to s0
     * Convert bit sum to 32-bit sum
               mcw  +s0+31, x1         * x1 = right end of s0
               mcw  @032@, x2          * Process 32 bits
               b    sum
               sw   s0                 * Restore wordmark cleared by sum
     

     
               mcw  x1tmp, x1
               mcw  s0+31, 543&x1      * Move s0 to w[i]
       
              
               ma   @032@, x1
               a    +1, i
               mz   @0@, i
               b    wloop
     
     x1tmp     dcw  #5
     

     * Initialize: Copy hex h0init-h7init into binary h0-h7
     wloopd    mcw  +h0init-7, x3
               mcw  +h0, x1
               mcw  @064@, tobinc       * 8*8 hex digits
               b    tobin
     
     
     * Initialize a-h from h0-h7
               mcw  @000@, x1
     ilp       mcw  h0+31&x1, a+31&x1
               ma   @032@, x1
               c    x1, @256@
               bu   ilp
     
               mcw  @000@, bitidx      * bitidx = i*32 = bit index
               mcw  @000@, kidx        * kidx = i*8 = key index
                

     * Compute s1 from e        
     mainlp    mcw  +e, x1
               mcw  +s1, x2
               za   +0, 31&x2               * Zero s1
     * Add e rightrotate 6
               sw   6&x2               * Wordmark at bit 6 (from left) of s1
               a    25&x1, 31&x2       * Right shifted: 31-6 = bit 25 of e, 31 = end of s1
               a    31&x1, 5&x2        * Wrapped: 31 = end of e, 6-1 = bit 5 of s1   
               cw   6&x2               * Clear wordmark
     * Add e rightrotate 11
               sw   11&x2              * Wordmark at bit 11 (from left) of s1
               a    20&x1, 31&x2       * Right shifted: 31-11 = bit 20 of e, 31 = end of s1
               a    31&x1, 10&x2       * Wrapped: 31 = end of e, 11-1 = bit 10 of s1   
               cw   11&x2              * Clear wordmark
     * Add e rightrotate 25
               sw   25&x2              * Wordmark at bit 25 (from left) of s1
               a    6&x1, 31&x2        * Right shifted: 31-25 = bit 6 of e, 31 = end of s1
               a    31&x1, 24&x2       * Wrapped: 31 = end of e, 25-1 = bit 24 of s1   
               cw   25&x2              * Clear wordmark
     * Convert sum to xor
               mcw  +s1+31, x1         * x1 = right end of s1
               mcw  @032@, x2          * Process 32 bits
               b    xor
               sw   s1                 * Restore wordmark cleared by xor

     * Compute ch: choose function
               mcw  @000@, x1          * x1 is index from 0 to 31
     chl       c    e&x1, @0@
               be   chzero
               mn   f&x1, ch&x1        * for 1, select f bit
               b    chincr
     chzero    mn   g&x1, ch&x1        * for 0, select g bit
     chincr    a    +1, x1
               mz   @0@, x1
               c    @032@, x1
               bu   chl

     * Compute temp1: k[i] + h + S1 + ch + w[i]
               cs   299
               mcw  +k-7, x3            * Convert k[i] to binary in temp1
               ma   kidx, x3
               mcw  +temp1, x1
               mcw  @008@, tobinc       * 8 hex digits
               b    tobin
               mcw  @237@, x3
               mcw  +temp1, x1
               mcw  @008@, tobinc
               b    tohex
               a    h+31, temp1+31     * +h
               a    s1+31, temp1+31    * +s1
               a    ch+31, temp1+31    * +ch
               mcw  bitidx, x1
               a    warr+31&x1, temp1+31         * + w[i]
     * Convert bit sum to 32-bit sum
               mcw  +temp1+31, x1      * x1 = right end of temp1
               b    sum
  

     * Compute s0 from a
               mcw  +a, x1
               mcw  +s0, x2
               za   +0, 31&x2               * Zero s0
     * Add a rightrotate 2
               sw   2&x2               * Wordmark at bit 2 (from left) of s0
               a    29&x1, 31&x2       * Right shifted: 31-2 = bit 29 of a, 31 = end of s0
               a    31&x1, 1&x2        * Wrapped: 31 = end of a, 2-1 = bit 1 of s0   
               cw   2&x2               * Clear wordmark
     * Add a rightrotate 13
               sw   13&x2              * Wordmark at bit 13 (from left) of s0
               a    18&x1, 31&x2       * Right shifted: 31-13 = bit 18 of a, 31 = end of s0
               a    31&x1, 12&x2       * Wrapped: 31 = end of a, 13-1 = bit 12 of s0   
               cw   13&x2              * Clear wordmark
     * Add a rightrotate 22
               sw   22&x2              * Wordmark at bit 22 (from left) of s0
               a    9&x1, 31&x2        * Right shifted: 31-22 = bit 9 of a, 31 = end of s0
               a    31&x1, 21&x2       * Wrapped: 31 = end of a, 22-1 = bit 21 of s0   
               cw   22&x2              * Clear wordmark
     * Convert sum to xor
               mcw  +s0+31, x1         * x1 = right end of s0
               mcw  @032@, x2          * Process 32 bits
               b    xor
               sw   s0                 * Restore wordmark cleared by xor

     * Compute maj(a, b, c): majority function
               za   +0, maj+31
               a    a+31, maj+31
               a    b+31, maj+31
               a    c+31, maj+31
               mz   @0@, maj+31
               mcw  @000@, x1          * x1 is index from 0 to 31
     mjl       c    maj&x1, @2@
               bh   mjzero
               mn   @1@, maj&x1       * majority of the 3 bits is 1
               b    mjincr
     mjzero    mn   @0@, maj&x1       * majority of the 3 bits is 0
     mjincr    a    +1, x1
               mz   @0@, x1
               c    @032@, x1
               bu   mjl

     * Compute temp2: S0 + maj
               za   +0, temp2+31
               a    s0+31, temp2+31
               a    maj+31, temp2+31
     * Convert bit sum to 32-bit sum
               mcw  +temp2+31, x1      * x1 = right end of temp1
               b    sum
     
               mcw  g+31, h+31         * h := g
               mcw  f+31, g+31         * g := f
               mcw  e+31, f+31         * f := e
               za   +0, e+31           * e := d + temp1
               a    d+31, e+31
               a    temp1+31, e+31
               mcw  +e+31, x1          * Convert sum to 32-bit sum
               b    sum
               mcw  c+31, d+31         * d := c
               mcw  b+31, c+31         * c := b
               mcw  a+31, b+31         * b := a
               za   +0, a+31           * a := temp1 + temp2
               a    temp1+31, a+31
               a    temp2+31, a+31
               mcw  +a+31, x1          * Convert sum to 32-bit sum
               b    sum

               a    @8@, kidx          * Increment kidx by 8 chars
               mz   @0@, kidx
               ma   @032@, bitidx      * Increment bitidx by 32 bits
               c    @!48@, bitidx      * Compare to 2048
               bu   mainlp

     * Add a-h to h0-h7
               cs   299
               mcw  @00000@, x1tmp  
     add1      mcw  x1tmp, x1
               a    a+31&x1, h0+31&x1
               ma   +h0+31, x1          * Convert sum to 32-bit sum
               b    sum     
               ma   @032@, x1tmp
               c    @00256@, x1tmp
               bu   add1
               mcw  @201@, x3
               mcw  +h0, x1
               mcw  @064@, tobinc
               b    tohex
               w
               mcw  280, 180
               p
               p

     finis     h
               b    finis

      
     * Converts sum of bits to xor
     * X1 is right end of word
     * X2 is bit count    
     * Note: clears word marks
     xor       sbr  xorx&3
     xorl      c    @000@, x2
               be   xorx
     xorfix    mz   @0@, 0&x1          * Clear zone
               c    0&x1, @2@
               bh   xorok
               sw   0&x1               * Subtract 2 and loop
               s    +2, 0&x1
               cw   0&x1
               b    xorfix
     xorok     ma   @I9I@, x1         * x1 -= 1
               s    +1, x2             * x2 -= 1
               mz   @0@, x2
               b    xorl               * loop
     
     xorx      b    @000@
     
     * Converts sum of bits to sum (i.e. propagate carries if digit > 1)
     * X1 is right end of word
     * Ends at word mark
     sum       sbr  sumx&3
     suml      mz   @0@, 0&x1          * Clear zone
               c    0&x1, @2@          * If digit is <2, then ok
               bh   sumok
               s    +2, 0&x1           * Subtract 2 from digit
               bwz  suml, 0&x1, 1      * Skip carry if at wordmark
               a    @1@, 15999&x1      * Add 1 to previous position
               b    suml               * Loop
     sumok     bwz  sumx,0&x1,1        * Quit if at wordmark
               ma   @I9I@, x1          * x1 -= 1
               b    suml               * loop
     sumx      b    @000@              * return
     
     * Converts binary to string of hex digits
     * X1 points to start (left) of binary
     * X3 points to start (left) of hex buffer
     * X1, X2, X3 destroyed
     * tobinc holds count (# of hex digits)
     tohex     sbr  tohexx&3
     tohexl    c    @000@, tobinc      * check counter
               be   tohexx
               s    @1@, tobinc        * decrement counter
               mz   @0@, tobinc
               b    tohex4
               mcw  hexchr, 0&x3
               ma   @004@, X1
               ma   @001@, X3
               b    tohexl             * loop
     tohexx    b    @000@ 
     

     
     * X1 points to 4 bits
     * Convert to hex char and write into hexchr
     * X2 destroyed

     tohex4    sbr  tohx4x&3
               mcw  @000@, x2
               c    3&X1, @1@
               bu   tohx1
               a    +1, x2
     tohx1     c    2&X1, @1@
               bu   tohx2
               a    +2, x2
     tohx2     c    1&x1, @1@
               bu   tohx4
               a    +4, x2
     tohx4     c    0&x1, @1@
               bu   tohx8
               a    +8, x2
     tohx8     mz   @0@, x2
               mcw  hextab-15&x2, hexchr
     tohx4x    b    @000@
     
     * Converts string of hex digits to binary
     * X3 points to start (left) of hex digits
     * X1 points to start (left) of binary digits
     * tobinc holds count (# of hex digits)
     * X1, X3 destroyed
     tobin     sbr  tobinx&3
     tobinl    c    @000@, tobinc      * check counter
               be   tobinx
               s    @1@, tobinc        * decrement counter
               mz   @0@, tobinc
               mcw  0&X3, hexchr
               b    tobin4             * convert 1 char
               ma   @004@, X1
               ma   @001@, X3
               b    tobinl             * loop
     tobinx    b    @000@
               
     
     tobinc    dcw  @000@
     * Convert hex digit to binary
     * Digit in hexchr (destroyed)
     * Bits written to x1, ..., x1+3
     tobin4    sbr  tobn4x&3
               mcw  @0000@, 3+x1   * Start with zero bits
               bwz  norm,hexchr,2  * Branch if no zone
              
               mcw  @1@, 0&X1
               a    @1@, hexchr    * Convert letter to value: A (1) -> 2, F (6) -> 7
               mz   @0@, hexchr
               b    tob4
     norm      c    @8@, hexchr
               bl   tob4
               mcw  @1@, 0&X1
               s    @8@, hexchr
               mz   @0@, hexchr
     tob4      c    @4@, hexchr
               bl   tob2
               mcw  @1@, 1&X1
               s    @4@, hexchr
               mz   @0@, hexchr
     tob2      c    @2@, hexchr
               bl   tob1
               mcw  @1@, 2&X1
               s    @2@, hexchr
               mz   @0@, hexchr
     tob1      c    @1@, hexchr
               bl   tobn4x
               mcw  @1@, 3&X1
     tobn4x    b    @000@          


     
     * Message schedule array is 64 entries of 32 bits = 2048 bits.
               org  3000
     warr      equ  3000
     
     s0        equ  warr+2047                *32 bits
     s1        equ  s0+32 
     ch        equ  s1+32              *32 bits

     temp1     equ  ch+32               *32 bits
     
     temp2     equ  temp1+32                *32 bits
     
     maj       equ  temp2+32                *32 bits
     
     a         equ  maj+32
     b         equ  a+32
     c         equ  b+32
     d         equ  c+32
     e         equ  d+32
     f         equ  e+32
     g         equ  f+32
     h         equ  g+32
     h0        equ  h+32
     h1        equ  h0+32
     h2        equ  h1+32
     h3        equ  h2+32
     h4        equ  h3+32
     h5        equ  h4+32
     h6        equ  h5+32
     h7        equ  h6+32
               org  h7+32
 
     hexchr    dcw  @0@
     hextab    dcw  @0123456789abcdef@    
     i         dcw  @00@               * Loop counter for w computation
     bitidx    dcw  #3
     kidx      dcw  #3         
     
     * 64 round constants for SHA-256
     k         dcw  @428a2f98@
               dcw  @71374491@
               dcw  @b5c0fbcf@
               dcw  @e9b5dba5@
               dcw  @3956c25b@
               dcw  @59f111f1@
               dcw  @923f82a4@
               dcw  @ab1c5ed5@
               dcw  @d807aa98@
               dcw  @12835b01@
               dcw  @243185be@
               dcw  @550c7dc3@
               dcw  @72be5d74@
               dcw  @80deb1fe@
               dcw  @9bdc06a7@
               dcw  @c19bf174@
               dcw  @e49b69c1@
               dcw  @efbe4786@
               dcw  @0fc19dc6@
               dcw  @240ca1cc@
               dcw  @2de92c6f@
               dcw  @4a7484aa@
               dcw  @5cb0a9dc@
               dcw  @76f988da@
               dcw  @983e5152@
               dcw  @a831c66d@
               dcw  @b00327c8@
               dcw  @bf597fc7@
               dcw  @c6e00bf3@
               dcw  @d5a79147@
               dcw  @06ca6351@
               dcw  @14292967@
               dcw  @27b70a85@
               dcw  @2e1b2138@
               dcw  @4d2c6dfc@
               dcw  @53380d13@
               dcw  @650a7354@
               dcw  @766a0abb@
               dcw  @81c2c92e@
               dcw  @92722c85@
               dcw  @a2bfe8a1@
               dcw  @a81a664b@
               dcw  @c24b8b70@
               dcw  @c76c51a3@
               dcw  @d192e819@
               dcw  @d6990624@
               dcw  @f40e3585@
               dcw  @106aa070@
               dcw  @19a4c116@
               dcw  @1e376c08@
               dcw  @2748774c@
               dcw  @34b0bcb5@
               dcw  @391c0cb3@
               dcw  @4ed8aa4a@
               dcw  @5b9cca4f@
               dcw  @682e6ff3@
               dcw  @748f82ee@
               dcw  @78a5636f@
               dcw  @84c87814@
               dcw  @8cc70208@
               dcw  @90befffa@
               dcw  @a4506ceb@
               dcw  @bef9a3f7@
               dcw  @c67178f2@
     * 8 initial hash values for SHA-256
     h0init    dcw  @6a09e667@
     h1init    dcw  @bb67ae85@
     h2init    dcw  @3c6ef372@
     h3init    dcw  @a54ff53a@
     h4init    dcw  @510e527f@
     h5init    dcw  @9b05688c@
     h6init    dcw  @1f83d9ab@
     h7init    dcw  @5be0cd19@


     input0    equ  h7init+64
               org  h7init+65

               dc   @80000000000000000000000000000000@
     input     dc   @00000000000000000000000000000100@      * 512 bits with the mostly-zero padding

               end  start

I punched the executable onto a deck of about 85 cards, which you can see at the beginning of the article. I also punched a card with the input to the hash algorithm. To run the program, I loaded the card deck into the card reader and hit the "Load" button. The cards flew through the reader at 800 cards per minute, so it took just a few seconds to load the program. The computer's console (below) flashed frantically for 40 seconds while the program ran. Finally, the printer printed out the resulting hash (as you can see at the top of the article) and the results were punched onto a new card. Since Bitcoin mining used double SHA-256 hashing, hashing for mining would take twice as long (80 seconds).

The console of the IBM 1401 shows a lot of activity while computing a SHA-256 hash.

Performance comparison

The IBM 1401 can compute a double SHA-256 hash in 80 seconds. It requires about 3000 Watts of power, roughly the same as an oven or clothes dryer. A basic IBM 1401 system sold for $125,600, which is about a million dollars in 2015 dollars. On the other hand, today you can spend $50 and get a USB stick miner with a custom ASIC integrated circuit. This USB miner performs 3.6 billion hashes per second and uses about 4 watts. The enormous difference in performance is due to several factors: the huge increase in computer speed in the last 50 years demonstrated by Moore's law, the performance lost by using a decimal business computer for a binary-based hash, and the giant speed gain from custom Bitcoin mining hardware.

To summarize, to mine a block at current difficulty, the IBM 1401 would take about 5x10^14 years (about 40,000 times the current age of the universe). The electricity would cost about 10^18 dollars. And you'd get 25 bitcoins worth about $6000. Obviously, mining Bitcoin on an IBM 1401 mainframe is not a profitable venture. The photos below compare the computer circuits of the 1960s with the circuits of today, making it clear how much technology has advanced.

On the left, SMS cards inside the IBM 1401. Each card has a handful of components and implements a circuit such as a gate. The computer contains more than a thousand of these cards. On the right, the Bitfury ASIC chip for mining Bitcoins does 2-3 Ghash/second. Image from zeptobars (CC BY 3.0 license)

Networking

You might think that Bitcoin would be impossible with 1960s technology due to the lack of networking. Would one need to mail punch cards with the blockchain to the other computers? While you might think of networked computers as a modern thing, IBM supported what they call teleprocessing as early as 1941. In the 1960s, the IBM 1401 could be hooked up to the IBM 1009 Data Transmission Unit, a modem the size of a dishwasher that could transfer up to 300 characters per second over a phone line to another computer. So it would be possible to build a Bitcoin network with 1960s-era technology. Unfortunately I didn't have teleprocessing hardware available to test this out.

IBM 1009 Data Transmission Unit. This dishwasher-sized modem was introduced in 1960 and can transmit up to 300 characters per second over phone lines. Photo from Introduction to IBM Data Processing Systems.

Conclusion

Implementing SHA-256 in assembly language for an obsolete mainframe was a challenging but interesting project. Performance was worse than I expected (even compared to my 12 minute Mandelbrot). The decimal arithmetic of a business computer is a very poor match for a binary-optimized algorithm like SHA-256. But even a computer that predates integrated circuits can implement the Bitcoin mining algorithm. And, if I ever find myself back in 1960 due to some strange time warp, now I know how to set up a Bitcoin network.

The Computer History Museum in Mountain View runs demonstrations of the IBM 1401 on Wednesdays and Saturdays so if you're in the area you should definitely check it out (schedule). Tell the guys running the demo that you heard about it from me and maybe they'll run my Pi program for you. Thanks to the Computer History Museum and the members of the 1401 restoration team, Robert Garner, Ed Thelen, Van Snyder, and especially Stan Paddock. The 1401 team's website (ibm-1401.info) has a ton of interesting information about the 1401 and its restoration.

Disclaimers

I would like to be clear that I am not actually mining real Bitcoin on the IBM 1401—the Computer History Museum would probably disapprove of that. As I showed above, there's no way you could make money off mining on the IBM 1401. I did, however, really implement and run the SHA-256 algorithm on the IBM 1401, showing that mining is possible in theory. And if you're wondering how I found a successful hash, I simply used a block that had already been mined: block #286819.