The 8085's register file reverse engineered

On the surface, a microprocessor's registers seem like simple storage, but not in the 8085 microprocessor. Reverse-engineering the 8085 reveals many interesting tricks that make the registers fast and compact. The picture below shows that the registers and associated control circuitry occupy a large fraction of the chip, so efficiency is important. Each bit is implemented with a surprisingly compact circuit. The instruction set is designed to make register accesses efficient. An indirection trick allows quick register exchanges. Many register operations use the unexpected but efficient data path of going through the ALU.

While the 8085's register complement is tiny compared to current processors, it has a solid register set by 1977 standards - about twice as many registers as the 6502. The 8085 has a 16-bit program counter, a 16-bit stack pointer, 16-bit BC, DE, and HL register pairs, and the 8-bit accumulator. The 8085 also has little-known hidden registers that are invisible to the programmer but used internally: the WZ register pair, and two 8-bit registers for the ALU: ACT and TMP.

Photograph of the 8085 chip showing components relevant to register operations.

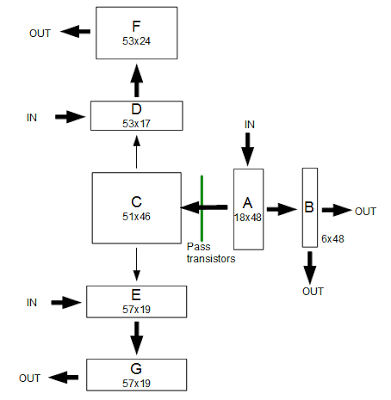
The register file is in the lower left quadrant of the chip. It contains the 6 register pairs and associated circuitry. Underneath the registers is the 16-bit address latch and increment/decrement circuit. The register file is controlled by a set of control lines on the right, which are driven by register control logic circuits and the register control PLA. The current instruction is loaded into the instruction register (upper right) via the data bus. In the upper left is the 8-bit arithmetic-logic unit (ALU), with the accumulator and two temporary registers (ACT and TMP).

The 8085 has only 40 pins (visible around the edge of the image) to communicate with the outside world, a tiny number compared to current microprocessors with more than 1000 pins. For memory accesses, the 8085 reads or writes 8 bits of data using a 16-bit memory address (for a maximum of 64K of memory). In the image above, memory addresses flow through the 16-bit address bus (abus) provides memory addresses, while data flows through the chip over the 8-bit data bus (dbus). The 8 A pins handle half of the address, while the 8 AD pins are used both for the other half of the address and for data (at different times). This frees up pins for other uses, but makes computers using the 8085 slightly more complicated. In comparison, the 6502 is more straightforward, with separate pins for address and data.

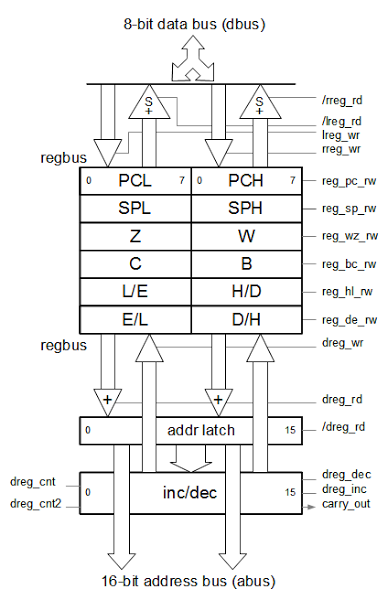
Overall architecture of the register file

The diagram below shows the implementation of the 8085 register file in the same layout as on the actual chip. The 8-bit data bus is at the top, and the 16-bit address bus is at the bottom. The register control lines are on the right.

In the middle are the registers, arranged as pairs of 8-bit registers. Note that the registers are arranged "backwards" with the high-order bit on the right and the low-order bit on the left. The 16-bit program counter and stack pointer are first. Next is the WZ temporary register, and underneath it the BC register pair. The HL and DE register pairs are at the bottom - these registers do not have fixed locations, but can swap roles during execution. A 16-bit register bus (regbus) provides access to the registers.

Underneath the registers is the address latch, which holds a 16-bit value that is written to the address bus. This value is also the input to the 16-bit increment/decrement circuit. The output of the incrementer/decrementer can be written back to the registers.

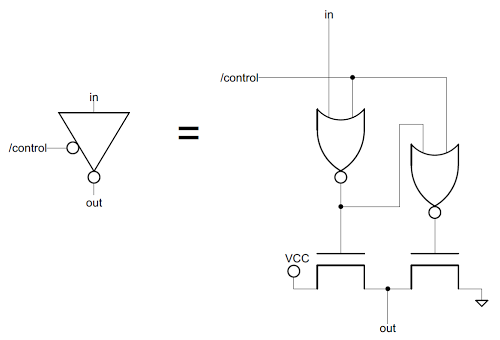
The triangles indicate tri-state buffers, basically switches that control the flow of data. Buffers containing a + are amplifiers to boost the weak signals from the registers. Buffers containing a S are superbuffers, that provide extra current to send data across the long data bus.

Architecture diagram of the 8085 register file, as it is implemented on the chip. The register file is connected to the data bus at top, and address bus at bottom. The control lines are along the right.

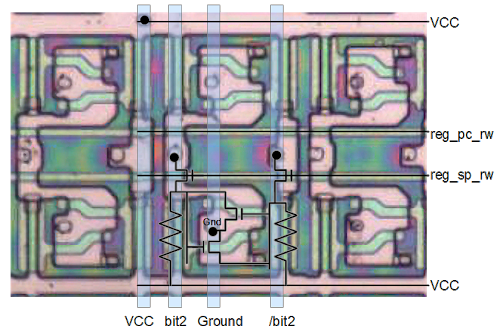
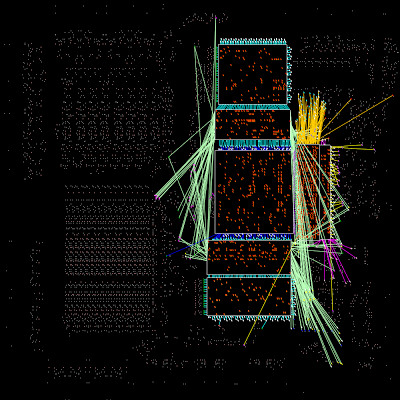
The picture below zooms in on the chip image above, showing the register file in detail. The components in silicon exactly map onto the diagram above. Note the repeated patterns for the 16-bit circuits. The large transistors used as high-current drivers are clearly visible. The transistors in each bit of register storage are much smaller.

A closeup of the 8085 microprocessor, showing the details of the register file and the locations of the major components.

Storing bits in the register file

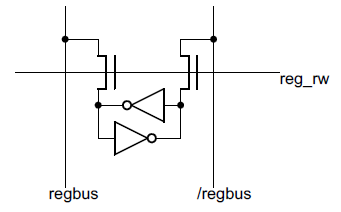
The implementation of the 8085 registers is unusual in several ways. The registers don't have explicit read and write modes; instead the register will be overwritten if there is a stronger signal on the bus. Instead of having a bus with one wire for each bit, the 8085 uses a sort of differential bus, with two wires for each bit: one wire transmits the value, and the other transmits the complement of the value.

Each bit consists of two inverters in a feedback loop, with pass transistors to connect the inverters to the bus. An unusual feature of this is the lack of any circuit to break the feedback loop when modifying the register (unlike the 6502). Instead, the 8085 uses a "might makes right" technique - if a stronger signal is written to the bus, it will overwrite a register connected to the bus. The transistors driving the register bus are about twice as large as the transistors in the inverters, so they can forcibly overwrite the inverter loop.

One consequence of this register implementation is that a register can't be copied directly to another register, since there's nothing to distinguish the source register from the destination register - each register could potentially damage the other's bits. To get around this, the 8085 uses an interesting trick - copies are actually done through the ALU, as will be explained later.

One bit of a register in the 8085 register file. Each bit is stored in two inverters in a feedback loop. The register bus uses two lines of opposite polarity for each bit. Access to the register is controlled by the reg_rw control line, which connects the inverters to the bus, allowing the value to be read or written.

The image below zooms in on the chip closer, showing the silicon for six individual register bits. The schematic for one bit is overlaid, as are some of the metal lines providing power, ground, and the register bus. Each bit consists of two transistors for the inverters, two depletion pullup transistors for the inverters (shown as resistors), and two pass transistors connecting the bit to the register bus. The pink regions are transistors, with the green strips the gates (details).

Detail of the 8085 chip showing six bits in the 8085's register file. Bit 2 of the stack pointer is shown with schematic. The two transistors form two inverters in a feedback loop. The light blue lines are the metal layer wires connected to bit 2. The program counter is in the upper half of the image.

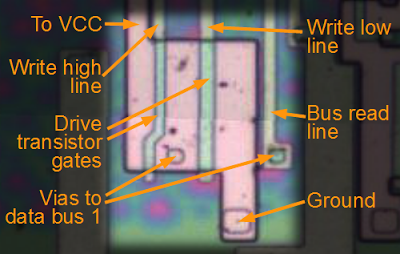
To read a register, an amplifier circuit is used to boost the signal from the differential register bus to write it to the dbus or address latch. I assume this is a tradeoff to make the register file smaller. Each inverter pair can be made as small as possible, but then requires amplification to produce a signal strong enough for use elsewhere in the chip. The amplification circuit that drives the data bus is more complex than I'd expect, probably because of the extra power to drive the bus (details and schematic).

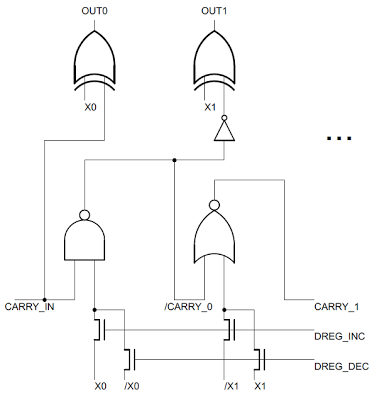
The incrementer/decrementer

The 16-bit incrementer/decrementer at the bottom of the register file is used for multiple purposes. It increments the program counter as instructions execute, increments and decrements the stack pointer as needed, and supports the 16-bit increment and decrement instructions.

An interesting feature of the incrementer is it also supports incrementing by 2, which is used to quickly skip over the two byte address in a call or jump not taken. This allows these operations to complete faster on the 8085 than the 8080.

Two bits of the 16-bit increment/decrement circuit in the 8085. Odd bits and even bits use a different circuit for efficiency. The carry out from even bits is complemented.

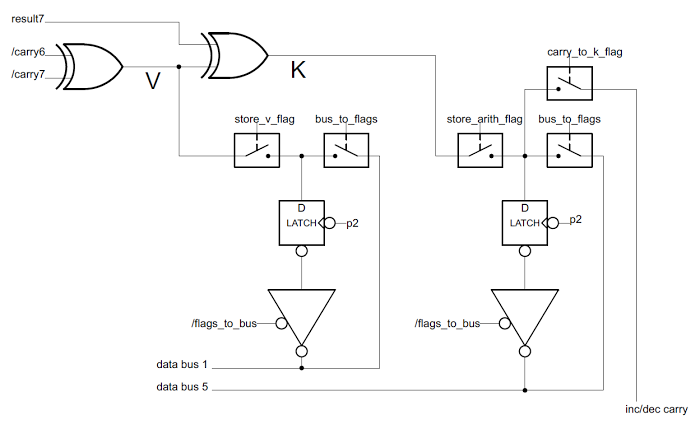
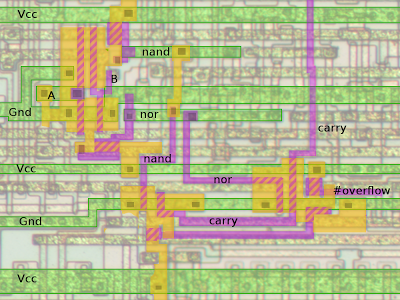
The incrementer/decrementer is implemented by a chain of adders with ripple carry - the carry from each bit flows into the adder for the next bit. (The above schematic shows two bits, and is repeated 8 times in the full circuit.) The DREG_INC and DREG_DEC control lines select increment or decrement. One performance trick is that alternating bits are implemented with different circuits and the carry out of even bits is inverted. This avoids the inverters that would otherwise be needed to flip the carry back to its regular state. This saves space, but even more importantly it speeds up carry propagation. Because the carry has to propagate bit-by-bit through all 16 bits to generate the final result, adding an inverter to each bit would slow it down significantly. The carry out is used to compute the undocumented K flag value (details).

In comparison, the 6502 has a 16-bit incrementer (no decrement) used exclusively by the program counter. To reduce the carry propagation speed, this incrementer uses a carry-skip. That is, the carry out of the low-order byte is immediately generated and fed into the high-order byte. Thus the carries only need to propagate through 8-bits, the two bytes working in parallel. (The carry is easily generated by ANDing together the low-order bits. If they are all 1, there will be a carry into the high-order byte.)

The WZ Temporary registers

The WZ register pair in the 8085 is used for temporary storage, but is invisible to the programmer. Internally, the WZ register pair is implemented like the other register pairs.

The primary use of WZ is to hold operands from a two or three byte instruction until it can be used. The WZ registers are used to hold 16-bit addresses for LDA, STA, LHLD, JMP, CALL, and RST instructions. The registers hold the port for IN and OUT. The WZ register pair can also temporarily hold information read from memory. The registers hold the address popped off the stack for RET. For XTHL, the registers hold the value from the stack.

Register decoding and the instruction set

The instruction set of the 8085 is organized so an instruction can be quickly and easily decoded to determine the instruction to use. The underlying structure for most 8085 instructions is the octal bit pattern bbDDDSSS, where destination bits DDD and/or source bits SSS select the register usage. The move (MOV) instructions follow this structure. Other instructions (e.g. INR) use just the DDD bits to select the register, while math instructions use the three SSS bits. Some instructions only use DDD or SSS, and some instructions operate on register pairs so they don't use the lowest bit. This instruction pattern is visible if the instructions are arranged in an instruction table according to their octal values.

The three bits select the register as follows:

D2D1D0	Register
000	B
001	C
010	D
011	E
100	H
101	L
110	M
111	A

M indicates a memory operation and is treated as a pseudo-register in the instruction set. Some instructions (e.g. INX) use the top two bits to select a register pair: BC, DE, HL, or "special" (stack pointer or accumulator). Note that in the table above the low-order bit selects a register out of a register pair.

This instruction set structure allows simple logic to control the registers. A multiplexer pulls out the right group of three bits, depending on the instruction and the cycle in the instruction (link to schematic). These three bits are then used to pick the specific register control lines to activate at each step.

The registers are controlled by about 18 control lines that affect the movement of data and the operation of the incremented/decrementer. The following table summarizes the control lines.

/RREG_RD	Reads the right-hand side register bus onto the data bus. This implements the multiplexing of 16-bit registers onto the 8-bit data bus.
/LREG_RD	Reads the left-hand side register bus onto the data bus.
LREG_WR	Writes the data bus to the left-hand side register bus. This implements the demultiplexing of the 8-bit data bus to the 16-bit registers.
RREG_WR	Writes the data bus to the right-hand side register bus.
REG_PC_RW	Connects the PC to the register bus.
REG_SP_RW	Connects the SP to the register bus.
REG_WZ_RW	Connects the WZ register pair to the register bus.
REG_BC_RW	Connects the BC register pair to the register bus.
REG_HL_RW	Connects the HL (DE) register pair to the register bus.
REG_DE_RW	Connects the DE (HL) register pair to the register bus.
DREG_WR	Writes the output of the incrementer/decrementer to the register bus.
DREG_RD	Reads the register bus into the address latch.
/DREG_RD	Inverted DREG_RD.
DREG_DEC	Incrementer/decrementer performs decrement.
DREG_INC	Incrementer/decrementer performs increment.
CARRY_OUT	The carry/borrow out from the incrementer/decrementer.
DREG_CNT	Increment/decrement by 1.
DREG_CNT2	Increment/decrement by 2.

The first step in register control is the register control PLA, which generates 19 control signals based on the instruction type and the cycle step. The register control logic (between the register file and the PLA) mixes in the register selection bits as appropriate (and a few other inputs) to generate the register control lines listed above.

For instance, REG_BC_RW control line is activated if the PLA indicates a register access and the register bits are 00x. The RREG_RD control line is activated for a single-register read instruction if the register bits are xx0, and LREG_RD is activated if the bits are xx1. Both control lines are activated at the same time if the PLA indicates a register pair read.

The DE/HL exchange trick

The XCHG instruction exchanges the contents of the HL register pair with the contents of the DE register pair in a single M-cycle. You might wonder how the registers can be exchanged so quickly. It turns out that this instruction is implemented with a trick - an extra level of indirection.

Although most 8085 architecture diagrams label one register pair as DE and another as HL, this isn't exactly true. In fact, the 8085 has two register pairs and either one can be the DE or HL pair. A status flip flop keeps track of which pair is DE and which is HL. As Pavel Zima figured out, the XCHG instruction doesn't move any data; it simply toggles the flip flop. The data remains in the same place, but the DE register is now HL and vice versa. Thus, the XCHG instruction is completed quickly. The consequence is every use of DE or HL uses this flip flop to determine which register to access (link to schematic).

Using the ALU to move registers

You wouldn't expect the ALU (arithmetic-logic unit) to take part in a register-to-register move, but it happens in the 8085. Many register operations take advantage of the ALU's temporary registers.

The ALU doesn't directly operate on the accumulator and input register. Instead, the accumulator is copied to the ACT (Accumulator Temporary) register and the other input is copied to the TMP register. This way, the result can be written to the accumulator without the race condition that would occur if the accumulator were an input and output at the same time.

For register moves, the source value is copied to the TMP register, the ACT register is set to 0, and the ALU performs an OR operation (ALU details), writing the result (i.e. the source value) to the dbus. This result can then be stored to the register file during a later cycle.

The register file in action

The step-by-step operation of the register file is surprisingly complex. One complication is that the register file and buses must handle stepping the program counter, fetching the instruction, and performing any register moves, without interference. A second complication is that register moves go through the ALU as described above.

Stepping through an operation in detail will show the complexity of the register operations. The following shows the data flow for a MOV B,E instruction, which copies the contents of the E register into the B register.

To understand this table, a bit of background on 8085 instruction timing. An instruction cycle is broken down into one or more M (machine) cycles, where an 8-bit memory access can be done in one M cycle. Each M cycle is broken down into several T-states, where each T-state corresponds to one clock cycle. Each clock cycle has a low phase and a high phase.

The single-byte register-to-register MOV instruction takes one M cycle (M1), 4 T cycles, or 8 clock phases. Each clock phase is a separate line in the table. To make things more complicated, the activity for an instruction isn't entirely within its own instruction cycle. To improve performance, the 8085 uses simple pipelining, where the M1 opcode fetch of the next instruction overlaps with completion of the previous instruction.

The MOV B, E instruction (which copies the E register to the B register) is illustrated in the table below. The PC is copied to the incrementer latch at the end of the previous operation, and then is written to the address pins during the T1 cycle. The PC is updated with the incremented value at the end of the T2 cycle.

The instruction opcode is fetched in the T3 cycle, and at this point execution can start on the instruction. It's not until the T1 cycle of the next instruction that the register file swings into action. The E register is written to the dbus at the end of the T1 cycle. Then the ALU's TMP register is loaded from the dbus. The ALU's other argument, the ACT register is 0 at this point, and the ALU is configured to perform an OR operation. At the end of the (next instruction's) T3 cycle, the result of the ALU operation (i.e. the E register) is stored in the B register via the dbus. Meanwhile, the next instruction is getting fetched (grayed out).

Cycle	T/clock	PC action	Register action
	T4/0
	T4/1	PC → inc latch
M1 opcode fetch	T1/0	inc latch → address pins
	T1/1	inc latch → address pins
	T2/0
	T2/1	inc → PC
	T3/0		data pins → dbus → instruction reg
	T3/1
	T4/0
	T4/1	PC → inc latch
M1 opcode fetch	T1/0	inc latch → address pins
	T1/1	inc latch → address pins	E reg → dbus
	T2/0		dbus → TMP reg
	T2/1	inc → PC
	T3/0		data pins → dbus → instruction reg
	T3/1		ALU → dbus → B reg

Each step in the table above is activated by the appropriate register control lines. For instance, in T2/1, the PC is updated by triggering the reg_pc_rw and dreg_wr lines.

Conclusion

The 8085 has a complex register set, and it uses some interesting tricks to reduce the size of the chip and to optimize some operations. The register set is much harder to understand than I expected, but with careful examination it reveals its secrets.

Credits: The chip images are from visual6502.org. The visual6502 team did the hard work of dissolving chips in acid to remove the packaging and then taking many close-up photographs of the die inside. Pavel Zima converted these photographs into mask layer images, a transistor net, an 8085 simulator, and register file schematics (top, bottom).

See discussion at Hacker News. Thanks for visiting!

8085 instruction set: the octal table

The instruction set of the 8085 microprocessor has an underlying structure that becomes much clearer if expressed in an octal-based table, rather than usual hexadecimal-based table:

	\0_0	\0_1	\0_2	\0_3	\0_4	\0_5	\0_6	\0_7	\1_0	\1_1	\1_2	\1_3	\1_4	\1_5	\1_6	\1_7
\00_	NOP	LXI B,d16	STAX B	INX B	INR B	DCR B	MVI B,d8	RLC	MOV B,B	MOV B,C	MOV B,D	MOV B,E	MOV B,H	MOV B,L	MOV B,M	MOV B,A
\01_	dsub	DAD B	LDAX B	DCX B	INR C	DCR C	MVI C,d8	RRC	MOV C,B	MOV C,C	MOV C,D	MOV C,E	MOV C,H	MOV C,L	MOV C,M	MOV C,A
\02_	arhl	LXI D,d16	STAX D	INX D	INR D	DCR D	MVI D,d8	RAL	MOV D,B	MOV D,C	MOV D,D	MOV D,E	MOV D,H	MOV D,L	MOV D,M	MOV D,A
\03_	rdel	DAD D	LDAX D	DCX D	INR E	DCR E	MVI E,d8	RAR	MOV E,B	MOV E,C	MOV E,D	MOV E,E	MOV E,H	MOV E,L	MOV E,M	MOV E,A
\04_	RIM	LXI H,d16	SHLD a16	INX H	INR H	DCR H	MVI H,d8	DAA	MOV H,B	MOV H,C	MOV H,D	MOV H,E	MOV H,H	MOV H,L	MOV H,M	MOV H,A
\05_	ldhi r8	DAD H	LHLD a16	DCX H	INR L	DCR L	MVI L,d8	CMA	MOV L,B	MOV L,C	MOV L,D	MOV L,E	MOV L,H	MOV L,L	MOV L,M	MOV L,A
\06_	SIM	LXI SP,d16	STA a16	INX SP	INR M	DCR M	MVI M,d8	STC	MOV M,B	MOV M,C	MOV M,D	MOV M,E	MOV M,H	MOV M,L	HLT	MOV M,A
\07_	ldsi r8	DAD SP	LDA a16	DCX SP	INR A	DCR A	MVI A,d8	CMC	MOV A,B	MOV A,C	MOV A,D	MOV A,E	MOV A,H	MOV A,L	MOV A,M	MOV A,A
\20_	ADD B	ADD C	ADD D	ADD E	ADD H	ADD L	ADD M	ADD A	RNZ	POP B	JNZ a16	JMP a16	CNZ a16	PUSH B	ADI d8	RST 0
\21_	ADC B	ADC C	ADC D	ADC E	ADC H	ADC L	ADC M	ADC A	RZ	RET	JZ a16	rstv	CZ a16	CALL a16	ACI d8	RST 1
\22_	SUB B	SUB C	SUB D	SUB E	SUB H	SUB L	SUB M	SUB A	RNC	POP D	JNC a16	OUT d8	CNC a16	PUSH D	SUI d8	RST 2
\23_	SBB B	SBB C	SBB D	SBB E	SBB H	SBB L	SBB M	SBB A	RC	shlx	JC a16	IN d8	CC a16	jnk a16	SBI d8	RST 3
\24_	ANA B	ANA C	ANA D	ANA E	ANA H	ANA L	ANA M	ANA A	RPO	POP H	JPO a16	XTHL	CPO a16	PUSH H	ANI d8	RST 4
\25_	XRA B	XRA C	XRA D	XRA E	XRA H	XRA L	XRA M	XRA A	RPE	PCHL	JPE a16	XCHG	CPE a16	lhlx	XRI d8	RST 5
\26_	ORA B	ORA C	ORA D	ORA E	ORA H	ORA L	ORA M	ORA A	RP	POP PSW	JP a16	DI	CP a16	PUSH PSW	ORI d8	RST 6
\27_	CMP B	CMP C	CMP D	CMP E	CMP H	CMP L	CMP M	CMP A	RM	SPHL	JM a16	EI	CM a16	jk a16	CPI d8	RST 7

The large-scale structure of the instruction set is by quadrant (i.e. the top two bits): MOV instructions in the pink quadrant, arithmetic instructions in the cyan quadrant, increment, decrement, rotates in the yellow quadrant, and control flow (jump, call, return, push, pop, rst) in the purple quadrant. It's not totally regular, of course. Some instructions are wedged in where they can fit, for example the spot where memory-to-memory move (MOV M, M) would go is replaced by HLT.

Note how registers are controlled by an octal digit in the sequence B, C, D, E, H, L, M, and A. This is especially notable for the MOV instructions and arithmetic instructions. For instructions acting on register pairs, the structure is similar: BC, BC, DE, DE, HL, HL, SP, SP.

Although octal is unpopular now, early microprocessors were designed with octal in mind, using groups of three bits to select registers and operations. Now hexadecimal is popular, but when the opcodes are displayed in a hex-based table, the underlying structure of the instructions is obscured.

Note that the four blocks have been arranged for ease of display - strictly speaking they should be stacked vertically rather than a 2x2 grid. The table includes undocumented instructions, which are shown in lower case. Mouse over a cell to see the hex value of the instruction. Credits: original data from pastraiser.com 8085 instruction table.

How the 8085 decodes instructions internally

The 8085 uses a set of PLAs to decode and process instructions. In the first step of processing an instruction the instruction decode ROM (details) decodes the instruction into one of 48 different instruction groups. The grid below is colored according to the instruction group (0 through 47).

NOP

LXI B,d16 42

STAX B 40

INX B 36

INR B 38

DCR B 38

MVI B,d8 14

RLC 25

MOV B,B 45

MOV B,C 45

MOV B,D 45

MOV B,E 45

MOV B,H 45

MOV B,L 45

MOV B,M 44

MOV B,A 45

dsub 21

DAD B 20

LDAX B 41

DCX B 37

INR C 38

DCR C 38

MVI C,d8 14

RRC 25

MOV C,B 45

MOV C,C 45

MOV C,D 45

MOV C,E 45

MOV C,H 45

MOV C,L 45

MOV C,M 44

MOV C,A 45

arhl 24

LXI D,d16 42

STAX D 40

INX D 36

INR D 38

DCR D 38

MVI D,d8 14

RAL 25

MOV D,B 45

MOV D,C 45

MOV D,D 45

MOV D,E 45

MOV D,H 45

MOV D,L 45

MOV D,M 44

MOV D,A 45

rdel 22

DAD D 20

LDAX D 41

DCX D 37

INR E 38

DCR E 38

MVI E,d8 14

RAR 25

MOV E,B 45

MOV E,C 45

MOV E,D 45

MOV E,E 45

MOV E,H 45

MOV E,L 45

MOV E,M 44

MOV E,A 45

RIM 3

LXI H,d16 42

SHLD a16 12

INX H 36

INR H 38

DCR H 38

MVI H,d8 14

DAA 6

MOV H,B 45

MOV H,C 45

MOV H,D 45

MOV H,E 45

MOV H,H 45

MOV H,L 45

MOV H,M 44

MOV H,A 45

ldhi r8 23

DAD H 20

LHLD a16 13

DCX H 37

INR L 38

DCR L 38

MVI L,d8 14

CMA 6

MOV L,B 45

MOV L,C 45

MOV L,D 45

MOV L,E 45

MOV L,H 45

MOV L,L 45

MOV L,M 44

MOV L,A 45

SIM 3

LXI SP,d16 42

STA a16 8

INX SP 36

INR M 39

DCR M 39

MVI M,d8 16

STC 6

MOV M,B 43

MOV M,C 43

MOV M,D 43

MOV M,E 43

MOV M,H 43

MOV M,L 43

HLT 47

MOV M,A 43

ldsi r8 23

DAD SP 20

LDA a16 9

DCX SP 37

INR A 38

DCR A 38

MVI A,d8 14

CMC 6

MOV A,B 45

MOV A,C 45

MOV A,D 45

MOV A,E 45

MOV A,H 45

MOV A,L 45

MOV A,M 44

MOV A,A 45

ADD B 1

ADD C 1

ADD D 1

ADD E 1

ADD H 1

ADD L 1

ADD M 4

ADD A 1

RNZ 19

POP B 27

JNZ a16 29

JMP a16 30

CNZ a16 33

PUSH B 26

ADI d8 2

RST 0 5

ADC B 1

ADC C 1

ADC D 1

ADC E 1

ADC H 1

ADC L 1

ADC M 4

ADC A 1

RZ 19

RET 18

JZ a16 29

rstv 7

CZ a16 33

CALL a16 34

ACI d8 2

RST 1 5

SUB B 1

SUB C 1

SUB D 1

SUB E 1

SUB H 1

SUB L 1

SUB M 4

SUB A 1

RNC 19

POP D 27

JNC a16 29

OUT d8 17

CNC a16 33

PUSH D 26

SUI d8 2

RST 2 5

SBB B 1

SBB C 1

SBB D 1

SBB E 1

SBB H 1

SBB L 1

SBB M 4

SBB A 1

RC 19

shlx 10

JC a16 29

IN d8 15

CC a16 33

jnk a16 31

SBI d8 2

RST 3 5

ANA B 1

ANA C 1

ANA D 1

ANA E 1

ANA H 1

ANA L 1

ANA M 4

ANA A 1

RPO 19

POP H 27

JPO a16 29

XTHL 35

CPO a16 33

PUSH H 26

ANI d8 2

RST 4 5

XRA B 1

XRA C 1

XRA D 1

XRA E 1

XRA H 1

XRA L 1

XRA M 4

XRA A 1

RPE 19

PCHL 32

JPE a16 29

XCHG 46

CPE a16 33

lhlx 11

XRI d8 2

RST 5 5

ORA B 1

ORA C 1

ORA D 1

ORA E 1

ORA H 1

ORA L 1

ORA M 4

ORA A 1

RP 19

POP PSW 27

JP a16 29

DI 0

CP a16 33

PUSH PSW 26

ORI d8 2

RST 6 5

CMP B 1

CMP C 1

CMP D 1

CMP E 1

CMP H 1

CMP L 1

CMP M 4

CMP A 1

RM 19

SPHL 28

JM a16 29

EI 0

CM a16 33

jk a16 31

CPI d8 2

RST 7 5

Colors by iWantHue

The internal decoding shown above reveals a few interesting things. The NOP instruction is literally no operation - it doesn't get decoded into any instruction group. The MOV instructions are all decoded together, except for the memory operations. Similarly, the arithmetic instructions are all grouped together, except for the memory instructions. There are other smaller groups (e.g. INR/DCR, conditional jumps, conditional calls, returns), and 21 instructions that are handled uniquely(e.g. CALL, PCHL, XCHG, HALT, and 6 undocumented instructions). Surprisingly, DAA, CMA, STC, and CMC are handled together at this stage, despite having very different actions.

Silicon reverse engineering: The 8085's undocumented flags

The 8085 microprocessor has two undocumented status flags: V and K. These flags can be reverse-engineered by looking at the silicon of the chip, and their function turns out to be different from previous explanations. In addition, the implementation of these flags shows that they were deliberately implemented, which raises the question of why they were not documented or supported by Intel. Finally, examining how these flag circuits were implemented in silicon provides an interesting look at how microprocessors are physically implemented.

Like most microprocessors, the 8085 has a flag register that holds status information on the results of an operation. The flag register is 8 bits: bit 0 holds the carry flag, bit 2 holds the parity, bit 3 is always 0, bit 4 holds the half-carry, bit 6 holds the zero status, and bit 7 holds the sign. But what about the missing bits: 1 and 5?

Back in 1979, users of the 8085 determined that these flag bits had real functions.[1] Bit 1 is a signed-number overflow flag, called V, indicating that the result of a signed add or subtract won't fit in a byte.[2] Bit 5 of the flag is poorly understood and has been given the names K, X5, or UI. For an increment/decrement operation it simply indicates 16-bit overflow or underflow. But it has a totally diffrent value for arithmetic operations. The flag has been described[1][3] as:

K =  O1·O2 + O1·R + O2·R, where:
O1 = sign of operand 1
O2 = sign of operand 2
R = sign of result
For subtraction and comparisons, replace O2 with complement of O2.

As I will show, that published description is mistaken. The K flag actually is the V flag exclusive-ored with the sign of the result. And the purpose of the K flag is to compare signed numbers.

The circuit for the K and V flags

The following schematic shows the reverse-engineered circuit for the K and V flags in the 8085. The V flag is simply the exclusive-or of the carry into the top bit and the carry out of the top bit. This is a standard formula for computing overflow[2] for signed addition and subtraction. (The 6502 computes the same overflow value through different logic.) The V flag has values for other arithmetic operations, but the values aren't useful.[4] A latch stores the value of the V flag. The computed V value is stored in the latch under the control of a store_v_flag control signal. Alternatively, the flag value can be read off the bus and stored in the latch under the control of the bus_to_flags control signal; this is how the POP PSW instruction, which pops the flags from the stack, is implemented. Finally, a tri-state superbuffer (the large triangle) writes the flag value to the bus when needed.

The K flag circuitry is on the right. The first function of the K flag is overflow/underflow for an INX/DEX instruction. This is implemented simply: the carry_to_k_flag control line sets the K flag according to the carry from the incrementer/decrementer. The next function of K flag is reading from the databus for the POP PSW instruction, which is the same as for the V flag. The final function of the K flag is the result of a signed comparison. The K flag is the exclusive-or of the V flag and the sign bit of the result. For subtraction and comparison, the K flag is 1 if the second value is larger than the first.[5] The K flag is set for other arithmetic operations, but doesn't have a useful value except for signed comparison and subtraction.[4]

The circuit in the 8085 for the undocumented V and K flags. The flags are generated from the carries and results from the ALU. The K flag can also be set by the carry from the incrementer/decrementer.

One mystery was the purpose of the K flag: "It does not resemble any normal flag bit."[1] Its use for increment and decrement is clear, but for arithmetic operations why would you want the exclusive-or of the overflow and sign? It turns out the the K flag is useful for signed comparisons. If you're comparing two signed values, the first is smaller if the exclusive-or of the sign and overflow is 1.[6] This is exactly what the K flag computes.

From the circuit above, it is clear that the V and K flags were deliberately added to the chip. (This is in contrast to the 6502, where undocumented opcodes have arbitrary results due to how the circuitry just happens to work for unexpected inputs.[7]) Why would Intel add the above circuitry to the chip and then not document or support it? My theory is that Intel decided they didn't want to support K or (8-bit) V flags in the 8086, so in order to make the 8086 source-compatible with the 8085, they dropped those flags from the 8085 documentation, but the circuitry remained in the chip.

The silicon

The 8085 microprocessor showing the data bus, ALU, flag logic, registers, and incrementer/decrementer.

The remainder of this article will show how the V and K flag circuits work, diving all the way down to the silicon circuits. The above image of the 8085 chip shows the layout of the chip and the components that are important to the discussion. In the upper left of the chip is the ALU (arithmetic-logic unit), where computations happen (details). The data bus is the main interconnect in the chip, connects the data pins (upper left), the ALU, the data registers, the flag register, and the instruction decoding (upper right). In the lower left of the chip is the 16-bit register file. Underneath the register file is a 16-bit increment/decrement circuit which handles incrementing the program counter, as well as supporting 16-bint increment and decrement instructions. The increment/decrement circuit has a carry-out in the lower right corner - this will be important for the discussion of the K flag. For some reason, the ALU has the low-order bit on the right, while the registers have the low-order bit on the left.

The flag logic circuitry sits underneath the ALU, with high-current drivers right on top of the data bus. The flags are arranged in apparently-random order with bit 7 (sign) on the left and bit 6 (zero) on the right. Because the carry logic is much more complicated (handling not only arithmetic operations but shifts and rotates, carry complement, and decimal adjust), the carry logic is stuck off to the right of the ALU where there was enough room.

Zooming in

Next we will zoom in on the V flag circuitry, labeled V1 above. Looking at the die under a microscope shows the metal layer of the chip, consisting of mostly-horizontal metal interconnects, which are the white lines below. The bottom part of the chip has the 8-bit data bus. Other wires are the VCC power supply, ground, and a variety of signals. While modern processors can have ten or more metal layers, the 8085 only has a single layer. Some of the circuitry underneath the metal is visible.

The metal layer of the 8085 microprocessor, zoomed in on the V flag circuit.

If the metal is removed from the chip, the silicon layer becomes visible. The blotchy green/purple is plain silicon. The pink regions are N-type doped silicon. The grayish regions are polysilicon, which can be considered as simply conductive wires. When polysilicon crosses doped silicon, it forms a transistor, which appears light green in this image. Note that transistors form a fairly small portion of the chip; there is a lot more connection and wiring than actual transistors. The small squares are vias, connections to the metal layer.

The V flag circuit in the 8085 CPU. This is the silicon/polysilicon after the metal layer has been removed. The data bus is not visible as it is in the metal layer, but it is in the lower third of the image. The rectangles at the bottom connect the data bus to the registers.

MOSFET transistors

For this discussion, a MOSFET can be considered simply a switch that closes if the gate input is 1 and opens if the gate input is 0. A MOSFET transistor is implemented by separating two diffusion regions, and putting a polysilicon wire over the gate. An insulating layer prevents any current from flowing between the gate and the rest of the transistor. In the following diagram, the n+ diffusion regions are pink, the polysilicon gate conductor is dull green, and the insulating oxide layer is turquoise.

NOR gate

The NOR gate is a fundamental building block in the 8085, since it is a very simple gate that can form more complex logic. A NOR gate is implemented through two transistors and a pullup transistor. If either input (or both) is 1, the corresponding transistor connects the output to ground. Otherwise, the transistors are open, and the pullup pulls the output high. The pullup is shown as a resistor in the schematic, but it is actually a type of transistor called a depletion-mode transistor for better performance.

By zooming in to a single NOR gate in the 8085, we can see how the gate is actually implemented. One surprise is that the circuit is almost all wiring; the transistors form a very small part of the circuit. The two transistors are connected to ground on the left, and tied together on the right. The pullup transistor is much larger than the other transistors for technical reasons.[8]

To understand the circuit, trace the path from ground to each transistor, across the gate, and to the output. In this way you can see there are two paths from ground to the output, and if either input is 1 the output will be 0.

The layout of the gate is intended to be as efficient as possible, given the constraints of where the power (VCC), ground, and other connections are, yielding a layout that looks a bit unusual. The power, ground, and input signals are all in the metal layer above (not shown here), and are connected to this circuit through vias between the metal and the silicon below.

A NOR gate in the 8085 microprocessor, showing the components.If either input is high, the associated transistor will connect the output to ground. Otherwise the pullup transistor will pull the output high.

Exclusive-or gates

The exclusive-or circuit (which outputs a 1 if exactly one input is 1) is a key component of the flag circuitry, and illustrates how more complex logic can be formed out of simpler gates. The schematic below shows how the exclusive-or is built from a NOR gate and an AND-NOR gate; it is straightforward to verify that if both inputs are 0 or both inputs are 1, the output is will be 0.

You may wonder why the 8085 uses so many "strange" gates such as a combined AND-NOR, instead of "normal" gates like AND. The transistor-level schematic shows that an AND-NOR gate can actually be implemented very simply with MOSFETs, in fact simpler than a plain AND gate. The two rightmost transistors form the "AND" - if they both have 1 inputs, they connect the output to ground. The transistor to the left forms the other part of the NOR - if it has a 1 input, it pulls the output to ground.

The following diagram shows an XOR circuit in the 8085 that matches the schematic above. (This is the XOR gate that generates the K flag.) On the left is the NOR gate discussed above, and on the right is the AND-NOR circuit, both outlined with a dotted line. As before, the circuit is mostly wiring, with the transistors forming a small part of the circuit (the green regions between pink diffusion regions).

An XOR gate in the 8085 microprocessor, formed from a NOR gate and an AND-NOR gate. If both inputs are 0, the NOR gate output will be 1, and the NOR transistor will pull the output to 0. If both inputs are 1, the AND transistors will pull the output to 0. Otherwise the pullup transistor will pull the output 1.

The flag latch

Each flag bit is stored in a simple latch circuit made up of two inverters. To store a 1, the inverter on the right outputs a 0, which is fed into the inverter on the left, which outputs a 1, which is fed back to the inverter on the right. A zero is stored in a similar (but opposite) manner. When the clock input is low, the pass transistor opens, breaking the feedback loop, and new data can be written into the latch. The complemented output (/out) is taken from the inverter.

You might wonder why the latch doesn't lose its data whenever the clock goes low. There's an interesting trick here called dynamic logic. Because the gate of a MOSFET consists of an insulating layer it has very high resistance. Thus, any electrical charge on the gate will remain there for some time[9] when the pass transistor opens. When the pass transistor closes, the charge is refreshed.

The latch used in the 8085 to store a flag value. The latch uses two inverters to store the data. When the clock is low, a new value can be written to the latch.

The following part of the 8085 chip shows the implementation of the latch for the V flag. The circuit closely matches the schematic above. The two inverters are outlined with dotted lines. The red arrows show the flow of data through the circuit. As before, the wiring and pullup transistors take up most of the silicon real estate.

Each flag in the 8085 uses a two-inverter latch to store the flag. This shows the latch for the undocumented V flag. The red arrows show the flow of data.

Driving the data bus with a superbuffer

Another interesting feature of the flag circuit is the "superbuffer". Most transistors in the 8085 only send a signal a short distance. However, to send a signal on the data bus across the whole chip takes a lot more power, so a superbuffer is used. In the superbuffer, one transistor is driven to pull the output low, while a second transistor is driven to pull the output high. (This is in contrast to a regular gate, which uses a depletion-mode pullup transistor to pull the output high.) In addition, these transistors are considerably larger, to provide more current.[8] These two transistors are shown at the bottom the schematic below.

The other feature of this superbuffer is that it is tri-state. In addition to a 0 or 1 output, it has a third state, which basically consists of providing no output. This way, the flags do not affect the data bus except when desired. In the schematic, it can be seen that if the control input is 1, both NOR gates will output 0, and both transistors will do nothing.

The superbuffer used in the 8085 to drive the data bus.

The following diagram shows the two drive transistors, as well as the line used to read the flag from the data bus. (The NOR gates are not shown.) Note the size of these transistors compared to transistors seen earlier. Each flag bit requires a superbuffer such as this. Even flag bit 3, which is always 0, requires a large transistor to drive the 0 onto the bus - it's surprising that a do-nothing flag still takes up a fair bit of silicon.

Each flag in the 8085 uses a superbuffer to drive the value onto the data bus. This figure shows the two large transistors that drive the V flag onto bit 1 of the data bus.

Putting it all together

The above discussion has shown the details of the XOR gate that computes the K flag, and the latch and superbuffer for the V flag. The following diagram shows how these pieces fit into the overall circuitry. The latch and driver for the K flag are outside this image, to the right. The circuits below are tied together by the metal layer, which isn't shown. Compare this diagram with the schematic at the top of the article to see how the components are implemented. The two XOR circuits look totally different, since their layouts have been optimized to fit with the signals they need.

The 8085 circuits to implement the undocumented V and K flags. The ALU provides /carry6, /carry7, and result7. The XOR circuit on the left generates V, and the XOR circuit in the middle generates K. On the right are the latch for the V flag, and the superbuffer that outputs the flag to the data bus. The K flag latch and superbuffer are to the right, not shown.

By looking at the silicon chip carefully, the transistors, gates, and complex circuits start to make sense. It's amazing to think that the complex computers we use are built out of these simple components. Of course, processors now are way more complex than the 8085, with billions of transistors instead of thousands, but the basic principles are still the same.

If you found this discussion interesting, check out my earlier analysis of the 6502's overflow flag and the 8085's ALU. You may also be interested in the book The Elements of Computing Systems, which describes how to build a computer starting with Boolean logic.

Credits

The chip images are from visual6502.org. The visual6502 team did the hard work of dissolving chips in acid to remove the packaging and then taking many close-up photographs of the die inside. Pavel Zima converted these photographs into mask layer images, a transistor net, and an 8085 simulator.

Notes and references

[1] The undocumented instructions and flags of the 8085 were discovered by Wolfgang Sehnhardt and Villy M. Sorensen in the process of writing an 8085 assembler, and were written up in the article Unspecified 8085 op codes enhance programming, Engineer's Notebook, "Electronics" magazine, Jan 18, 1979 p 144-145.

[2] See my article The 6502 overflow flag explained mathematically for details on overflow. There are multiple ways of computing overflow, and the 6502 uses a different technique.

[3] Tundra Semiconductor sold the CA80C85B, a CMOS version of the 8085. Interestingly, the undocumented opcodes and flags are described in the datasheet for this part: CA80C85B datasheet, 8000-series components.

The interesting thing about the Tundra datasheet is the descriptions of the "new" flags and instructions are copied almost exactly from Dehnhardt's article except for the introduction of errors, missing parentheses, and renaming the K flag as UI. In addition, as I described earlier, the published K/UI flag formula doesn't always work. Thus, it appears that despite manufacturing the chip, Tundra didn't actually know how these circuits worked.

[4] The V flag makes sense for signed addition and subtraction, and the K flag makes sense for signed subtraction and comparison. Many other operations affect these flags, but the flags may not have any useful meaning.

The V flag is 0 for RRC, RAR, AND, OR, and XOR operations, since these operations have constant carry values inside the ALU (details). The RLC and RAL operations add the accumulator to itself, so they can be treated the same as addition: V is set if the signed result is too big for a byte. The V flag for DAA can also be understood in terms of the underlying addition: V will only be set if the top digit goes from 7 to 8. However, since BCD digits are unsigned, V has no useful meaning with DAA. DAD is an interesting case, since the V flag indicates 16-bit signed overflow; it is actually computed from the result of the high-order addition. For INR, the only overflow case is going from 0x7f to 0x80 (127 to -128); note that going from 0xff to 0x00 corresponds to -1 to 0, which is not signed overflow even though it is unsigned overflow. Likewise, DCR sets the V flag going from hex 80 to 7f (-128 to 127); likewise 0x00 to 0xff is not signed overflow.

The K flag has a few special cases. For AND, OR, and XOR, the K flag is the same as the sign, since the V flag is 0. Note that the K flag is computed entirely differently for INR/DCR compared to INX/DCX. For INR and DCR, the K flag is S^V, which almost always is S. The K flag is set for DAA if S^V is true, which doesn't have any useful meaning since BCD values are unsigned.

The published formula for the K flag gives the wrong value for XOR if both arguments are negative.

[5] The following table illustrates the 8 possible cases when comparing signed numbers A and B. The inputs are the top bit of A, the top bit of B, and the carry from bit 6 when subtracting B from A. The outputs are the carry, borrow (complement of carry), sign, overflow, and K flags. An example is given for each row. Note that the K flag is set if A is less than B when treated as signed numbers.

Inputs			Outputs					Example
A7	B7	C6	C	B	S	V	K	Hex	Signed comparison
0	1	0	0	1	0	0	0	0x50 - 0xf0 = 0x60	80 - -16 = 96
0	1	1	0	1	1	1	0	0x50 - 0xb0 = 0xa0	80 - -80 = -96
0	0	0	0	1	1	0	1	0x50 - 0x70 = 0xe0	80 - 112 = -32
0	0	1	1	0	0	0	0	0x50 - 0x30 = 0x120	80 - 48 = 32
1	1	0	0	1	1	0	1	0xd0 - 0xf0 = 0xe0	-48 - -16 = -32
1	1	1	1	0	0	0	0	0xd0 - 0xb0 = 0x120	-48 - -80 = 32
1	0	0	1	0	0	1	1	0xd0 - 0x70 = 0x160	-48 - 112 = 96
1	0	1	1	0	1	0	1	0xd0 - 0x30 = 0x1a0	-48 - 48 = -96

[6] A detailed explanation of signed comparisons is given in Beyond 8-bit Unsigned Comparisons by Bruce Clark, section 5. While this article is in the context of the 6502, the discussion applies equally to the 8085.

[7] The illegal opcodes in the 6502 are discussed in detail in How MOS 6502 Illegal Opcodes really work. In the 6502, the operations performed by illegal opcodes are unintended, just chance based on what the chip logic happens to do with unexpected inputs. In contrast, the undocumented opcodes in the 8085, like the undocumented flags, are deliberately implemented.

[8] The key parameter in the performance of a MOSFET transistor is the width to length ratio of the gate. Oversimplifying slightly, the current provided by the transistors is proportional to this ratio. (Width is the width of the source or drain, and length is the length across the gate from source to drain.) For an inverter, the W/L ratio of the pullup should be approximately 1/4 the W/L ratio of the input transistor for best performance. (See Introduction to VLSI Systems, Mead, Conway, p 8.) The result is that pullup transistors are big and blocky compared to pulldown transistors. Another consequence is that high-current transistors in a superbuffer have a very wide gate. The 8085 register file has some transistors where the W/L ratios are carefully configured so one transistor will "win" over the other if both are on at the same time. (This is why the 8085 simulator is more complex than the 6502 simulator, needing to take transistor sizes into account.)

[9] One effect of using pass-transistor dynamic buffers is that if the clock speed is too small, the charge will eventually drain away causing data loss. As a result the 8085 has a minimum clock speed of 500 kHz. Likewise, the 6502 has a minimum clock speed. The Z-80 in contrast is designed with static logic, so it has no minimum clock speed - the clock can be stepped as slowly as desired.

Inside the ALU of the 8085 microprocessor

The arithmetic-logic unit is a fundamental part of any computer, performing addition, subtraction, and logic operations, but how it works is a mystery to many people. I've reverse-engineered the ALU circuit from the 8085 microprocessor and explain how it works. The 8085's ALU is a surprisingly complex circuit that at first looks like a mysterious jumble of gates, but it can be understood if you don't mind diving into some Boolean logic.

The following diagram shows the location of the ALU in the 8085. The ALU is 8 bits wide, with the high-order bit on the left. The register file is the large block below the ALU. The registers are 16 bits wide, made up of pairs of 8-bit registers. Surprisingly, the register file has the high-order bit on the right, the opposite order from the ALU.

The ALU takes two 8-bit inputs, which I'll call A and X, and performs one of five basic operations: ADD, OR, XOR, AND, and SHIFT-RIGHT. As well, if the input X is inverted, the ALU can perform subtraction and complement operations. You might think SHIFT-LEFT is missing from this list. However, it is simply performed by adding the number to itself, which shifts it to the left one bit in binary. Note that the 8085 arithmetic operations are very basic. There is no multiplication or division operation - these were added in the 8086.

The ALU consists of 8 mostly-identical slices, one for each bit. For addition, each slice of the ALU adds the appropriate input bits, computing the sum A + X + carry-in, generating a sum bit and a carry-out bit. That is, each bit of the ALU implements a full adder. The logic operations simply operate on the two input bits: A AND X, A OR X, A XOR X. Shift-right simply outputs the A bit from the slice to the right.

ALU schematic

The following schematic shows one bit of the ALU. The schematic has roughly the same layout as the implementation on the chip, flowing from bottom to top. Eight of these circuits are stacked side-by-side, with the low-order bit on the right. Carries flow from right to left, and bits shifted right flow from left to right.

Negation

Starting at the bottom of the schematic, is the complex gate labeled Negation. This gate optionally selects a negated second argument by selecting either XN or /XN. (XN is the Nth bit of the second argument, which I'll call X. The / indicates the complement.) For most of the discussion below I'll assume XN is uncomplemented to keep things simpler.

Operation

Above the complement selector are a few gates labeled Operation that perform the desired 2-input operation. The NAND gate on the left generates either A NAND X or 1 based on the select_op1 control line. The OR gate on the right generates either A OR X or 1, based on the select_op2 control line. Combining these in the NAND gate yields four different possibilities:

select_op1	select_op2	Result
0	0	A NOR X
0	1	0
1	0	A NXOR X
1	1	A AND X

Note that instead of OR and XOR, the complemented value is produced by this circuit. This will be fixed in the next step.

Combine with carry

Above the operation circuit is the next block of gates labeled Combine with carry that generates the ALU output by merging the carry-in with the operation value via XOR.

To understand this circuit, first consider the following simple XOR circuit, which is used a couple times in the ALU. It can be understood fairly simply: if both inputs are 0 (top) or both inputs are 1 (bottom) then the output is 0.

Ignoring the shift_right circuit for a moment, the block of gates is simply the XOR circuit above. Note that XOR with 0 is a no-op, while XOR with 1 complements the value. And A XOR X XOR CARRY is the low-order bit of adding A, X, and CARRY.

The key point of this circuit is that the incoming carry is generated with the proper value to convert the operation output into the desired final result. The incoming carry /carry(N-1) is either 0, 1, or the complemented carry from bit N-1 as appropriate.

Op	Operation output	Carry	Result
or	A NOR X	1	A OR X
add	A NXOR X	/carry	A XOR X XOR CARRY
xor	A NXOR X	1	A XOR X
and	A AND X	0	A AND X
shift right	0	0	A(N+1)
complement	A NOR /X	1	A OR /X
subtract	A NXOR /X	/carry	A XOR /X XOR CARRY

Note that the carry-in line must have the right value in order to generate the appropriate output. For addition it passes the inverted carry from one bit to the next. But for OR, XOR, the line is set to 1. And for AND and SHIFT_RIGHT it is set to 0. As will be seen below, the carry circuitry generates the right value for the right operation.

The final aspect of this circuit is the shift-right circuit. With a 0 op input, 0 carry input, and shift_right set, the output is simply the bit from the right: A(N+1).

Generate carry

The circuit on the left, labeled Generate carry generates the carry out. It can generate three different outputs: 1, 0, or the (complemented) carry from the sum. If select_op2 is set, it will force the carry to 0. Otherwise if force_ncarry_1 is set, it will force the carry to 1. Otherwise, the carry is generated for the sum of A + X + carry-in through straightforward logic: If the carry-in is set, and one of the inputs is set, there will be a carry out. If both input bits are set, there will be a carry out.

Flags

The 8085 has a parity flag, which is 1 if the number of 1 bits is even, and 0 if the number of parity bits is odd. The parity flag is generated by XORing all the result bits together (and complementing). Each bit is XORed with the lower-order parity value by the parity circuit near the top of the schematic. The XOR circuit is the same circuit described above.

The zero flag is computed by a simple circuit: each result bit drives a transistor that will pull the zero line low if the bit is set. This forms an 8-input NOR gate, spread across the ALU.

The control lines

As seen in the schematic, the 8085 uses multiple control lines to control the activity inside the ALU. In total, the ALU provides 7 different operations and the following table summarizes the control lines that are used for each operation. It also lists the opcodes that use each ALU operation.

Operation	select_neg	select_op1	select_op2	shift_right	force_ncarry_1	Opcodes
or	0	0	0	0	1	ORA,ORI (and default)
add	0	1	0	0	0	INR,DCR,RLC,DAD,RAL,DAA,ADD,ADC,ADI,ACI (and undocumented LDSI,LDHI,RDEL)
xor	0	1	0	0	1	XRA,XRI
and	0	1	1	0	1	ANA,ANI
shift right	0	0	1	1	1	RRC,RAR (ARHL)
complement	1	0	0	0	1	CMA
subtract	1	1	0	0	0	SUB,SBB,SUI,SBI,CMP,CPI (DSUB)

The ALU control lines are generated from the opcode by the programmable logic array. Specifically, they are outputs from PLA F, which is to the right of the ALU. More details are in my article on the PLA. The ALU has additional control lines to set up the registers, initialize the carry bits, and set the flags. These control the differences between different op codes, beyond the categories above. the I will explain those in a future article.

Reverse-engineering the ALU

This information is based on the 8085 reverse-engineering done by the visual 6502 team. This team dissolves chips in acid to remove the packaging and then takes many close-up photographs of the die inside. Pavel Zima converted these photographs into mask layer images, generated a transistor net from the layers, and wrote a transistor-level 8085 simulator.

I took the transistor net and used it to figure out how the ALU works. First, I converted the transistor net into gates. Next I figured out which gates are part of the ALU and put them into a schematic. Then I examined how the circuit worked for different operations and eventually figured out how it works.

Conclusion

The ALU of the 8085 is an interesting circuit. At first it seemed like an incomprehensible pile of gates with mysterious control lines, but after some investigation I figured it out. The 8085 ALU is implemented very differently from the 6502's ALU (which I'll write up later). The 6502's ALU uses fairly straightforward circuits to generate the SUM, AND, XOR, OR, and SHIFT values in parallel, and then uses a simple pass-transistor multiplexor to pick the desired operation. This is in contrast to the 8085 ALU, which generates only the desired value.

Notes on the PLA on the 8085 chip

The 8085 processor uses a PLA (programmable logic array) to control much of the activity within the processor, such as instruction decoding and controlling the data flow between components of the chip. Pavel Zima has reverse-engineered the transistor-level circuitry of the 8085 microprocessor. I've looked into this in a bit more to figure out the architecture of the Programmable Logic Array, which takes up a large fraction of the chip. The PLA circuit is much more complex than the PLA on the 6502, for instance. It turns out that Pavel is ahead of me with information on the decode and timing PLAs, but the information below may still be of interest.

The following diagram shows the arrangement of the PLA on the chip (image from Visual 6502). The PLA has 5 planes, which I have labeled A through G.

The block diagram below shows approximately how the planes are connected. Plane A receives inputs from the instruction circuit. Its outputs are fed into the small plane B, producing outputs that go into the instruction circuit. The outputs from A also are fed into C (through pass transistors).

Planes D and E can be considered the same plane, split apart for better layout. They share 11 input lines, and the remaining inputs are different between D and E. These inputs come from the ALU/register circuits on the left, as well as other parts of the chip. They also receive inputs from G - these inputs are not handled via normal PLA input lines, but are wired through transistors directly to the associated output lines, which makes the layout more compact.

Planes F and G provide outputs through pass transistors to the ALU/register circuits. These outputs probably control the actions and bus activity, but more analysis is needed.

The following diagram shows how the PLA planes are wired to the rest of the chip. Planes D and E in particular receive inputs from many parts of the chip. The outputs from F and G are very short because the displayed wires end at the nearby pass transistors to the left.

The transistors in the PLA

I have diagrams showing where the transistors are in each PLA grid here.

The 6502 CPU's overflow flag explained at the silicon level

In this article, I show how overflow is computed in the 6502 microprocessor at the transistor and silicon level. I've discussed the mathematics of the 6502 overflow flag earlier and thought it would be interesting to look at the actual chip-level implementation. Even though the overflow flag is a slightly obscure feature, its circuit is simple enough that it can be explained at the silicon level.

The 6502 microprocessor chip

The 6502 is an 8-bit microprocessor that was very popular in the 1970s and 1980s, powering popular home computers such as the Apple II, Commodore PET, and Atari 400/800. The following photograph shows the die of a 6502 processor. Looking at the photograph, it seems impossibly complex, but it turns out that it actually can be understood, using the Visual 6502 group's reverse engineered 6502. The red box shows that part of the chip that will be explained in this article. The 6502 chip is made up of 4528 transistors (3510 enhancement transistors and 1018 depletion pullup transistors). (By comparison, a modern Xeon processor has over 2.5 billion transistors, which would be almost hopeless to try to understand.)

Photomicrograph of the 6502, from Visual 6502 (CC BY-NC-SA 3.0). The following diagrams zoom in on the red box, where the overflow circuit is located.

As a rough overview of the above photograph, the edge of the die shows the wires going to the pins. Approximately top fifth of the chip (with the regular rectangular pattern) is the PLA that decodes instructions. The middle third is a bunch of logic, mostly to do additional decoding of instructions. The bottom half has the registers, ALU (arithmetic-logic unit), and main busses. They are all 8 bits, with each bit in a horizontal layer. The high-order bit is at the bottom of the photo, and this is where the overflow logic lies.

The overflow formula

In brief, if an unsigned addition doesn't fit in a byte, the carry flag is set. But if a signed addition doesn't fit in a byte, the overflow flag is set. The 6502 processor computes the overflow bit for addition from the top bits of the two operands (A₇ and B₇), and the carry out of bit 6 into bit 7 (C₆):

V = not (((A7 NOR B7) and C6) NOR ((A7 NAND B7) NOR C6))

For a more detailed explanation of what overflow means, see my previous article or The overflow flag explained.

Gate-level implementation

Described as gates, the actual circuit to generate the overflow flag in the 6502 turns out to be surprisingly simple. It uses the carry out of bit 6, and the top bits of the two arguments A and B. Since the values of NAND(a7, b7) and NOR(a7, b7) are already available in the ALU (Arithmetic-Logic Unit) for other purposes, the actual overflow circuit is simply the three gates on the right. (The ALU is, of course, much more complex than the part shown above.) This circuit can be seen at the bottom of the 6507 schematic (where the inverted overflow value is called FLOW). You might wonder why the circuit uses NAND and NOR gates so heavily; it turns out that these are much easier to implement with transistors than AND and OR gates.

Transistor-level implementation

The transistors that implement the overflow circuit in the 6502 microprocessor. The circuits on the left compute the NAND and NOR of the top bits of A and B. The circuit on the right computes the overflow flag. Based on the remarkable transistor-level schematic of the full 6502 chip, reverse-engineered by Balazs.

The circuit above shows the actual implementation of the overflow circuit in the 6502 using NMOS transistors. The circuit to generate the overflow flag is very simple, requiring just a few transistors to implement the three gates. A, B, and carry are the inputs, and the output #overflow indicates complement of the overflow signal.

MOS transistors are fairly easy to understand, since they operate like switches. Most of the transistors are NMOS enhancement mode transistors, which can be considered as switches that close if the gate has a positive input, and are open otherwise. The transistors with a black bar are NMOS depletion mode transistors, which can be considered as pull-up resistors, giving a positive output if nothing else pulls the output low.

The three transistors on the left implement a simple logic gate to compute NAND of A and B. If both inputs A and B are positive, the switches close and connect the output to ground (the horizontal line at the bottom). Otherwise, the pullup transistor connects the output to the positive voltage (circle at the top). Thus, the output is the NAND of A and B - 0 if both inputs are positive, and 1 otherwise.

The next three transistors compute NOR of A and B. If A, B, or both are positive, the associated transistor is switched on and connects the output to ground. Otherwise the output is positive.

The remaining transistors are the actual overflow circuit. The next group of three transistors is a NOR gate, which was described above. It computes the NOR of the carry and the NAND output from the ALU, feeding its output into the final group of four transistors. The four transistors on the right implement an AND gate and NOR gate in a single circuit. If the output from the previous circuit is 1, the rightmost transistor switches on, pulling the output (inverted V) to ground. If both NOR7 and CARRY6 are 1, the two associated transistors switch on, pulling the output to ground. Otherwise, the pullup transistor keeps the output high. The result is the complemented overflow value.

Going to the silicon

Now that you've seen how the circuit works at the transistor level, the silicon level can be explained.

We'll begin with an (oversimplified) description of how the chip is constructed. The chip starts with the silicon wafer. Regions are diffused with an element such as boron, yielding conductive n⁺ diffusion regions. On top of the polysilicon layer is a layer of metal "wires" providing more connections. For our purposes, diffusion regions, polysilicon, and metal can all be consider conductors. In the 6502, the polysilicon connections run roughly vertical, and the metal wires run generally horizontal.

Structure of an NMOS transistor. The n⁺ diffusion regions (yellow) separated by undiffused silicon (gray). The gate is formed by an insulating oxide layer (red) with a diffusion line (purple) over it.

To build a transistor, two n⁺ regions are separated by an undiffused region. A thin insulating oxide layer on top forms the transistor gate, which is wired to a diffusion line. When charge is applied to the gate via the polysilicon line, the two n⁺ regions can conduct.

The follow picture zooms in on the base silicon layer in the 6502, showing the region in the red outline. The darker gray regions are n⁺ diffusion areas, which have been doped to be conducting. The white stripes that separate n⁺ regions are the transistor gates, showing the thin insulating oxide layer that switches on and off conduction between the neighboring n⁺ regions. The gray squares are vias, which connect to other layers.

The diffusion layer of the 6502, zoomed in on the overflow circuit. The shaded regions are diffusion regions, and the unshaded regions are undiffused silicon. The white strips show transistor gates. From Visual 6502 (CC BY-NC-SA 3.0).

The next picture shows the polysilicon and metal layers that lie on top of the base silicon. This picture is aligned with the previous one, and you may be able to pick out some of the diffusion layer underneath. The whitish vertical stripes are conductive polysilicon. The greenish metallic-looking horizontal stripes are in fact metal, forming conductors. The gray square are vias, which connect different layers. Note that the chip is crammed full of conductors, making it hard at first glance to tell what is going on.

Closeup of the 6502 microprocessor die, showing the overflow circuit. From Visual 6502 (CC BY-NC-SA 3.0).

The following picture shows approximately how the transistor-level circuit maps onto the silicon. This circuit is the same as the transistor schematic earlier, just drawn to match the actual layout on the chip. The A, B, and CARRY inputs come from other parts of the chip, and the inverted #OVERFLOW output exits on the right to other destinations.

The final picture explains exactly what is happening at the silicon level. It labels the different layers that take part in the overflow circuit with different colors. The lowest layer is the diffusion layer in yellow. On top of this is the polysilicon layer in purple. The topmost layer of metal is in green. Power (Vcc) and ground are supplied through the metal layer. The crosshatches show transistor gates, formed by polysilicon over insulating oxide. The skinny crosshatched areas are the enhancement transistors used as switches. The blocky crosshatched areas connected to Vcc (positive voltage) are the depletion transistors used as pullups.

The circuit can be understood starting in the upper left. A and B are bit 7 of the A and B values going into the ALU. (A and B come from elsewhere in the processor.) If A and B are positive, the two upper transistors (vertical crosshatches) will pull the NAND output low. If A or B are positive, one of the two transistors below will pull the NOR output low. The NAND and NOR outputs travel to multiple parts of the ALU through metal, polysilicon, and diffusion "wires", but only the relevant connections are shown.

In the lower left is the first gate of the overflow circuit, computing the NOR of the NAND output and carry (which comes from elsewhere in the chip). The polysilicon line (purple) on the bottom is the output from this gate. In the lower right is the second gate of the overflow circuit, combining the NOR, carry, and output of the first gate. The result is #overflow (i.e. inverted overflow).

You can see this circuit in action in the Visual 6502 simulator. The color scheme in the simulator is different - diffusion is green, yellow, orange, and red. The metal layer is shown in ghosted white, but Vcc and ground are omitted. Polysilicon is in purple, and the transistors are not explicitly shown.

Conclusions

By focusing on a simple circuit, the 6502 microprocessor chip can actually be understood at the silicon level. It's interesting to see how the complex patterns etched on the chip can be mapped onto gates, and their function understood.

More comments on this article are at Hacker News. Thanks for visiting!