Nelson Mandela tribute
The Bitcoin blockchain contains this image of Nelson Mandela and the tribute text. Someone encoded this data into fake addresses in Bitcoin transactions, causing it to be stored in the Bitcoin system.
"I am fundamentally an optimist. Whether that comes from nature or nurture, I cannot say. Part of being optimistic is keeping one’s head pointed toward the sun, one’s feet moving forward. There were many dark moments when my faith in humanity was sorely tested, but I would not and could not give myself up to despair. That way lays defeat and death."
"I learned that courage was not the absence of fear, but the triumph over it. The brave man is not he who does not feel afraid, but he who conquers that fear."
"Difficulties break some men but make others. No axe is sharp enough to cut the soul of a sinner who keeps on trying, one armed with the hope that he will rise even in the end."
"It always seems impossible until it’s done."
"When a man has done what he considers to be his duty to his people and his country, he can rest in peace."
"Real leaders must be ready to sacrifice all for the freedom of their
"Everyone can rise above their circumstances and achieve success if they are dedicated to and passionate about what they do."
"Education is the most powerful weapon which you can use to change the world."
"For to be free is not merely to cast off one’s chains, but to live in a way that respects and enhances the freedom of others."
"There is no passion to be found playing small – in settling for a life that is less than the one you are capable of living."
“There is nothing like returning to a place that remains unchanged to find the ways in which you yourself have altered.” -Nelson Mandela
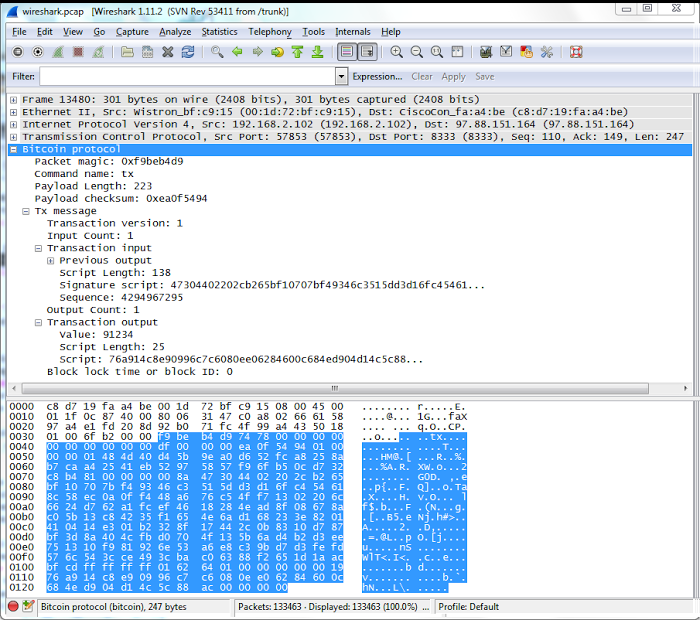
The data is stored in the blockchain by encoding hex values into the addresses. Below is an excerpt of one of the transactions storing the Mandela information. In this transaction, tiny amounts of bitcoins are being sent to fake addresses such as 15gHNr4TCKmhHDEG31L2XFNvpnEcnPSQvd. This address is stored in the blockchain as hex 334E656C736F6E2D4D616E64656C612E6A70673F. If you convert those hex bytes to Unicode, you get the string 3Nelson-Mandela.jpg?, representing the image filename. Similarly, the following addresses encode the data for the image. Thus, text, images, and other content can be stored in Bitcoin by using the right fake addresses.
Secret message in the first Bitcoin block
It is well known that the Genesis block, the very first block of data in Bitcoin contained a "secret" message. This message was stored in the coinbase[2], a part of a Bitcoin block that is filled in by the miner who mines a Bitcoin block. Along with the standard data, the original transaction also contains the message: 'The Times 03/Jan/2009 Chancellor on brink of second bailout for banks'[3]. Presumably this is a political commentary on Bitcoin compared to the insolvency of "real" banks.Bitcoin logo
People rapidly figured out how to encode arbitrary content into the Bitcoin blockchain by using hex data in place of Bitcoin addresses.[4] One of the first uses of this technique was to store the Bitcoin logo in the blockchain. I extracted the following image from the blockchain, where it was hidden among normal transactions.[5]
Prayers from miners
Early on, the miner Eligius started putting Catholic prayers in English and Latin in the coinbase field of blocks they mined. Here are some samples:Benedictus Sanguis eius pretiosissimus. Benedictus Iesus in sanctissimo altaris Sacramento. Ave Maria, gratia plena, Dominus tecum. Benedicta tu in mulieribus, ... ...and life everlasting, through the merits of Jesus Christ, my Lord and Redeemer. O Heart of Jesus, burning with love for us, inflame our hearts with love for Thee. Jesus, meek and humble of heart, make my heart like unto thine!These prayers turned out to be surprisingly controversial, leading to insults being exchanged through the blockchain: "
Oh, and god isn't real, sucka. Stop polluting the blockchain with your nonsense.",
"FFS Luke-Jr leave the blockchain alone!",
and a rickroll in response:
"Militant atheists, http://bit.ly/naNhG2 -- happy now?".[6]
The codebase technique has since been used by many other miners as advertising. Typical messages are:
Hi from 50BTC.com,
For Pierce and Paul,
Mined at GIVE-ME-COINS.com,
EclipseMC: Aluminum Falcon?,
Happy NY! Yours GHash.IO,
Mined By ASICMiner,
BTC Guild,
Made in China,
BitMinter,
/bitparking,
hi from poolserverj,
/ozcoin/stratum/,
/slush/.[7]
XSS demo
I've found JavaScript code in the blockchain that demonstrates a potential XSS attack. A common security hole on websites is cross-site scripting (XSS)[8], where an attacker can inject hostile JavaScript into a web page viewed by the victim. Surprisingly, such an attack was possible with Bitcoin. The transaction's output script was set to the hex corresponding to:
<script>window.alert("If this were an actual exploit, your mywallet would be empty.")</script>
Apparently some Bitcoin websites would fail to escape the tags, causing the script to run if you viewed the page.
The above script just created a harmless dialog box, but a more malicious transaction could potentially steal the user's bitcoins stored on the website.
Len Sassaman Tribute
A tribute to cryptographer Len Sassaman was put in the Bitcoin blockchain a couple weeks after his death by Dan Kaminsky.[9]
---BEGIN TRIBUTE---
#./BitLen
:::::::::::::::::::
:::::::.::.::.:.:::
:.: :.' ' ' ' ' : :
:.:'' ,,xiW,"4x, ''
: ,dWWWXXXXi,4WX,
' dWWWXXX7" `X,
lWWWXX7 __ _ X
:WWWXX7 ,xXX7' "^^X
lWWWX7, _.+,, _.+.,
:WWW7,. `^"-" ,^-'
WW",X: X,
"7^^Xl. _(_x7'
l ( :X: __ _
`. " XX ,xxWWWWX7
)X- "" 4X" .___.
,W X :Xi _,,_
WW X 4XiyXWWXd
"" ,, 4XWWWWXX
, R7X, "^447^
R, "4RXk, _, ,
TWk "4RXXi, X',x
lTWk, "4RRR7' 4 XH
:lWWWk, ^" `4
::TTXWWi,_ Xll :..
=-=-=-=-=-=-=-=-=-=
LEN "rabbi" SASSAMA
1980-2011
Len was our friend.
A brilliant mind,
a kind soul, and
a devious schemer;
husband to Meredith
brother to Calvin,
son to Jim and
Dana Hartshorn,
coauthor and
cofounder and
Shmoo and so much
more. We dedicate
this silly hack to
Len, who would have
found it absolutely
hilarious.
--Dan Kaminsky,
Travis Goodspeed
P.S. My apologies,
BitCoin people. He
also would have
LOL'd at BitCoin's
new dependency upon
ASCII BERNANKE
:'::.:::::.:::.::.:
: :.: ' ' ' ' : :':
:.: _.__ '.:
: _,^" "^x, :
' x7' `4,
XX7 4XX
XX XX
Xl ,xxx, ,xxx,XX
( ' _,+o, | ,o+,"
4 "-^' X "^-'" 7
l, ( )) ,X
:Xx,_ ,xXXXxx,_,XX
4XXiX'-___-`XXXX'
4XXi,_ _iXX7'
, `4XXXXXXXXX^ _,
Xx, ""^^^XX7,xX
W,"4WWx,_ _,XxWWX7'
Xwi, "4WW7""4WW7',W
TXXWw, ^7 Xk 47 ,WH
:TXXXWw,_ "), ,wWT:
::TTXXWWW lXl WWT:
----END TRIBUTE----
A creature simulator in Basic
I found a simple character-based simulator in Basic. The idea is 5 creatures wander around the screen eating food blocks and breeding or dying. Unfortunately the code has a bunch of bugs and doesn't work.[10]The original Bitcoin paper
In this transaction the Bitcoin blockchain contains the PDF for the original Bitcoin paper.
Rickrolls
Rickrolling is a popular internet prank, and Bitcoin is not immune. One rickroll was described above as part of the prayer dispute.[6] The lyrics to Never Gonna Give You Up! are found in a second rickroll.[11]A third rickroll has the song metadata and lyrics encoded in Base-64.[12]
Catagory: Poetry Title: Never Gonna Give You Up Performer: Rick Astley Writer: Mike Stock, Matt Aitken, Pete Waterman Label: RCA Records Released: 27, July, 1987 We're no strangers to love You know the rules and so do I A full commitment's what I'm thinking of You wouldn't get this from any other guy I just wanna tell you how I'm feeling Gotta make you understand Never gonna give you up, Never gonna let you down Never gonna run around and desert you ...
Photographs in a messaging system
Recently someone has built a message/storage system on top of Bitcoin that allows a growing sequence of messages, text, and images to be stored in the blockchain.[13]Among other things, this system contains text from the Bhagavad Gita, 1000 digits of pi, multiple JPG and PNG images, a Shel Silverstein poem, a Rumi poem, and quotes from a random party. Here are some of the images stored in the blockchain using this system:
Wikileaks cablegate data
A 2.5 megabyte Wikileak files ('cablegate-201012041811.7z') was embedded in the Bitcoin blockchain.[14] The data is followed by a message explaining how to access it.[15]Wikileaks Cablegate Backup cablegate-201012041811.7z Download the following transactions with Satoshi Nakamoto's download tool which can be found in transaction 6c53cd987119ef797d5adccd76241247988a0a5ef783572a9972e7371c5fb0cc Free speech and free enterprise! Thank you Satoshi! 5c593b7b71063a01f4128c98e36fb407b00a87454e67b39ad5f8820ebc1b2ad5 221d900b5ac701028f9dfab7dfba326f608308386d45c05432e721b7c122cba7 ... 128 lines of transaction ids deleted ...Downloading the data from the blockchain is inconvenient since the download tool needs to be used on the 130 chunks of 20 KB separately. (It's much easier to download the file from the internet.)
The blockchain contains the source code for Python tools to insert data into the blockchain and to download it.[16] In a weird self-referential twist, the downloader can be used to download itself. The uploader/downloader puts data into the destination address, but extends the previous technique by using Bitcoin escrow / multi-sig to put three addresses in each destination. It also uses a checksum to make storage more reliable.
Here's the code in the blockchain to insert data into the blockchain. While it says it was written by Satoshi Nakamoto (the pseudonymous author of Bitcoin), that's probably not true.
Leaked firmware key and illegal primes
This transaction has a link about a leaked private key, followed by 1K of hex bytes as text, which supposedly is the private key for some AMI firmware.The change from that transaction was used for this transaction, which references the Wikipedia page on illegal primes, followed by two supposedly-illegal primes from that page.
The change from that transaction was then used for the Wikileaks Cablegate messages, implying the same person was behind all these messages. It looks like someone was trying to store a variety of dodgy stuff in the Bitcoin blockchain, either to cause trouble or to make some sort of political point.
Email from Satoshi Nakamoto
The following email message allegedly from Bitcoin inventor Satoshi Nakamoto appears in the blockchain.[17] (It's almost certainly not really from him.) It seems to be referring to the removal of some Script opcodes from the Bitcoin server earlier and making the corresponding change to the Electrum server. My guess is this message is someone pointing out a bug fix for Electrum in a joking way.From a3a61fef43309b9fb23225df7910b03afc5465b9 Mon Sep 17 00:00:00 2001 From: Satoshi Nakamoto <[email protected]> Date: Mon, 12 Aug 2013 02:28:02 -0200 Subject:[PATCH] Remove (SINGLE|DOUBLE)BYTE I removed this from Bitcoin in f1e1fb4bdef878c8fc1564fa418d44e7541a7e83 in Sept 7 2010, almost three years ago. Be warned that I have not actually tested this patch. --- backends/bitcoind/deserialize.py | 8 +------- 1 file changed, 1 insertion(+), 7 deletions(-) diff --git a/backends/bitcoind/deserialize.py b/backends/bitcoind/deserialize.py index 6620583..89b9b1b 100644 --- a/backends/bitcoind/deserialize.py +++ b/backends/bitcoind/deserialize.py @@ -280,10 +280,8 @@ opcodes = Enumeration("Opcodes", [ "OP_WITHIN", "OP_RIPEMD160", "OP_SHA1", "OP_SHA256", "OP_HASH160", "OP_HASH256", "OP_CODESEPARATOR", "OP_CHECKSIG", "OP_CHECKSIGVERIFY", "OP_CHECKMULTISIG", "OP_CHECKMULTISIGVERIFY", - ("OP_SINGLEBYTE_END", 0xF0), - ("OP_DOUBLEBYTE_BEGIN", 0xF000), "OP_PUBKEY", "OP_PUBKEYHASH", - ("OP_INVALIDOPCODE", 0xFFFF), + ("OP_INVALIDOPCODE", 0xFF), ]) @@ -293,10 +291,6 @@ def script_GetOp(bytes): vch = None opcode = ord(bytes[i]) i += 1 - if opcode >= opcodes.OP_SINGLEBYTE_END and i < len(bytes): - opcode <<= 8 - opcode |= ord(bytes[i]) - i += 1 if opcode <= opcodes.OP_PUSHDATA4: nSize = opcode -- 1.7.9.4
Text in Bitcoin addresses
Bitcoin addresses are 34 characters long, so it is possible to put something interesting in the text address, although there are limitations.
The first option for putting text into an address is to test millions or billions of private keys by brute force in the hope of randomly getting a few characters you want in the public address. This generates a "vanity" address which is a valid working Bitcoin address.
An example is Bitcoin Armory, which uses the donation address 1ArmoryXcfq7TnCSuZa9fQjRYwJ4bkRKfv. Note that only six desirable characters were found, and the rest are random.
You can use the vanitygen command-line tool
or a website like bitcoinvanity to generate these addresses.
Many people have recently received tiny spam payments from vanity addresses with the prefixes 1Enjoy... and 1Sochi... addresses. These payments don't get confirmed by miners and the purpose of them is puzzling.
The second option is to use whatever ASCII address you want (starting with a 1 and ending with a six-character checksum). Since there is no known private key for this address, any bitcoins sent to this address are lost forever. Despite this, some addresses have received significant amounts: 1BitcoinEaterAddressDontSendf59kuE. has received over 1.6 bitcoins (over $1000). 1111111111111111111114oLvT2 (hex 0) has received almost 3 bitcoins.
A very strange activity is the large-scale deliberate "burning" of bitcoins by sending them to 1CounterpartyXXXXXXXXXXXXXXXUWLpVr, where nobody can ever use them. Amazingly, this address has received over 2,130 bitcoins (about $1.5 million dollars worth) that are now lost forever. The motivation is that Counterparty is issuing their own crypto-currency (XCP) in exchange for destroyed bitcoins. The idea is that "proof-of-burn" is a more fair way of distributing currency than mining.
Mysterious encrypted data in the blockchain
There are many mysterious things in the blockchain that I couldn't figure out, that appear to be encrypted data.Between June and September 2011, there were thousands of tiny mystery transactions from a few addresses to hundreds of thousands of random addresses sorted in decreasing order. These transactions are for 1 to 45 Satoshis, and have never been redeemed. As far as I can tell, the data is totally random. But maybe there is a secret message in the addresses or in the amounts. In any case, someone went to a lot of work to do this, so there must be some meaning. [20]
One interesting thing is that the change address from the cablegate description was then used for three 86 kilobyte GPG-encoded files.[18] From the "magic numbers" at the beginning of these files I know that these are GPG files encrypted using CAST5, but what is in these files is a mystery. Without the passphrase, they can't be decrypted.
By following the change addresses, we can see that after submitting the "Satoshi" uploader and downloader, the same person submitted the Bitcoin PDF. The same person then submitted five mysterious files.[19] These files appear entirely random, so they may contain encrypted data.
Valentine's day messages
There are a bunch of Valentine's day messages in the blockchain from a couple days ago. I assume someone set up a service to do this.How to put your own message in the blockchain
It's pretty easy to put your own 20-character message into the blockchain. The following steps explain how.- Take your 20-character string and convert it to hex. E.g. in Python:
'//righto.com/bc'.encode('hex') - Convert the resulting hex string to an address. An easy way is online:
https://blockchain.info/q/hashtoaddress/your hex value
yields
1AXJnNiDijKUnY9UJZkV5Ggdgh36aWDBYj. - Send bitcoins to that address and your message will show up in the blockchain when your transaction gets mined. Important: those bitcoins will be lost forever, so send a very small amount, like 10 cents. My test message can be seen at the end of blk00113 here.
Summary
People have found a variety of ways to store strange things in the Bitcoin blockchain. I have touched on some of them here, but undoubtedly there are many other hidden treasures.The notes to this article provides hashes for the interesting transactions, in case anyone wants to investigate further.
Notes and references
[1]
Clients store the 16-gigabyte blockchain in the data directory. On Windows, this is C:\Users\userid\AppData\Roaming\Bitcoin. The blocks are stored in a sequence of 128 megabyte files blknnnnnn.dat. Syncing these files is why a full Bitcoin client takes hours to start up.
An easy way to see the ASCII contents of the blockchain is to visit bitcoinstrings.com.
[2] In the Bitcoin protocol, every mined block has a transaction that creates new bitcoins. Part of that transaction is an arbitrary coinbase field of up to 100 bytes in the Script language. Normally the coinbase field has data such as the block number, timestamp, difficulty, and an arbitrary nonce number.
The full coinbase in the genesis block is:
PUSHDATA: 04 bits value (mining difficulty): FFFF001D PUSHDATA: 01 nonce value: 04 PUSHDATA: 45 'The Times 03/Jan/2009 Chancellor on brink of second bailout for banks': 5468652054696D65732030332F4A616E2F32303039204368616E63656C6C6F72206F6E206272696E6B206F66207365636F6E64206261696C6F757420666F722062616E6B73
[3] The message in the Genesis block is slightly different from the actual newspaper article: Chancellor Alistair Darling on brink of second bailout for banks.
[4]
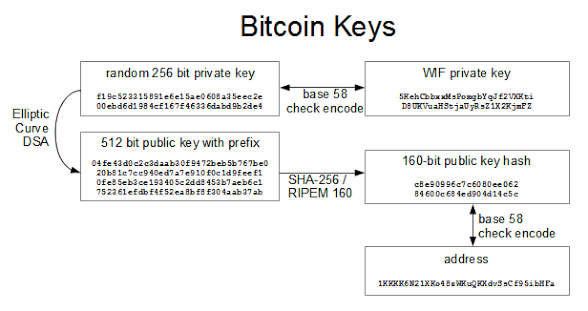
A brief overview of Bitcoin addresses will make this technique easier to understand. Normally, you start with a random 256-bit private key, which is necessary to redeem Bitcoins. From this, you generate a public key, which is hashed to a 160-bit address. This address is displayed in ASCII using a technique called Base58Check encoding. This ASCII address, such as 1LLLfmFp8yQ3fsDn7zKVBHMmnMVvbYaAE6, is the address used for transferring Bitcoins. But inside the transaction, the address is stored as the 160-bit (20 byte) hex value.
In normal use, you have no control over the 20-byte hex value used as an address. The trick for storing data in the transaction is to replace the address with 20 bytes of data that you want to store. For instance, the string This is my test data turns into the hex data '54686973206973206d7920746573742064617461'. If you send some bitcoins to that address, the bitcoins are lost forever (since you don't have the private key matching that address), but your message is now recorded in the Bitcoin blockchain.
See my earlier article for details on how Bitcoin addresses are generated.
[5] The Bitcoin logo was hidden in two transactions: ceb1a7fb57ef8b75ac59b56dd859d5cb3ab5c31168aa55eb3819cd5ddbd3d806 and 9173744691ac25f3cd94f35d4fc0e0a2b9d1ab17b4fe562acc07660552f95518.
If you look at the first ScriptPubKey of the first transaction, the address is 3d79626567696e206c696e653d3132382073697a, which turns into the ASCII text =ybegin line=128 siz. If you do this for all the addresses, you get an ecoded file. This file turns out to be encoded in the obscure yEnc encoding, designed in 2001 for transmitting binaries on Usenet.
I hacked together some code to extract and decode the file, resulting in the
bitcoin.jpg file shown above.
There was some discussion of this logo in 2011, but I don't know if anyone has actually extracted the image until now.
[6] The prayers can be found in blk00003 and blk00004. Eligius is appropriately named after Saint Eligius the patron saint of goldsmiths and coin collectors. The Rickroll is here.
[7]
For a while, the mysterious message /P2SH/ appeared in the coinbase field over and over. This string is an indication that the miner supports the pay-to-script-hash Bitcoin feature. The purpose of this was to ensure that more than 50% of the miners supported the feature before it was rolled out.
[8]
The XSS attack demo is in transaction
59bd7b2cff5da929581fc9fef31a2fba14508f1477e366befb1eb42a8810a000.
The JavaScript for the attack was put in the transaction's output script. The blockchain.info website displays the contents of the output script, but apparently didn't escape it as HTML. Thus, the contents <script> would not be displayed as text, but would be executed as part of the page. The demo only popped up an alert box, rather than running malicious JavaScript.
The creator of the attack describes it on Reddit.
[9] A talk presents some details on the tribute (here). The data is in transaction 930a2114cdaa86e1fac46d15c74e81c09eee1d4150ff9d48e76cb0697d8e1d72. This tribute cost 1 BTC, 0.01 BTC per line.
[10] The Basic code is in block 3a1c1cc760bffad4041cbfde56fbb5e29ea58fda416e9f4c4615becd65576fe7, and it is stored in "uploader" format, with a donation to Satoshi's genesis block address 1A1zP1eP5QGefi2DMPTfTL5SLmv7DivfNa.
Unfortunately the code is a mess with GOSUBs without RETURNs, broken loops, half-implemented ideas, and unused variables, so the code doesn't work, which is disappointing. It's a mystery why someone would put this BASIC code into the blockchain.
[11] The Rick Astley lyrics are in transaction d29c9c0e8e4d2a9790922af73f0b8d51f0bd4bb19940d9cf910ead8fbe85bc9b. This data is included using the OP_RETURN technique, which was later supported as a non-hacky way to put data into the blockchain.
[12]
The third rickroll has the data encoded in a structured format, maybe from some music database.
The data format is
[13]
The messaging system references "AtomSea & EMBII", who I assume are the creators.
The chain started with address 12KPNWdQ3sesPzMGHLMHrWbSkZvaeKZgHt with 0.269 BTC on 2013-12-01 23:54:35
Each output is 0.000055 bitcoins, just over the current network minimum of .0000546 bitcoin.
The next transaction in the chain can be found by looking at each change address, which pays for the next block.
The chain ended when it ran out of bitcoins, at address 1DQwj8BDLWy9BMzX8uUcDYze3hx8q7uBy4.
In total, the data chain has 85KB of data including images, random quotes, and HTML. The system embeds filenames, lengths, and the data. There are also a lot of transaction ids stored in the data, presumably serving as an index.
[14]
The 2.5 megabyte Cablegate file was stored in 130 separate transactions each holding 20,000 bytes of data, transactions
5c593b7b71063a01f4128c98e36fb407b00a87454e67b39ad5f8820ebc1b2ad5 to
2663cfa9cf4c03c609c593c3e91fede7029123dd42d25639d38a6cf50ab4cd44#o6".
Each transaction includes a trivial 0.00000001 bitcoin donation to the Wikileaks donation address 1HB5XMLmzFVj8ALj6mfBsbifRoD4miY36v.
This data is stored in checksummed download tool format.
[15] The cablegate description is in 691dd277dc0e90a462a3d652a1171686de49cf19067cd33c7df0392833fb986a, and is stored in "uploader" format. It's a bit circular that this message describes where to find the download tool, but the message itself needs the download tool to be read. Fortunately it's not too hard to read the message without the tool.
[16] The uploader is in transaction 4b72a223007eab8a951d43edc171befeabc7b5dca4213770c88e09ba5b936e17". The downloader is in transaction 6c53cd987119ef797d5adccd76241247988a0a5ef783572a9972e7371c5fb0cc.
In a cute touch, these transactions both donate 0.00000001 bitcoins to address 1A1zP1eP5QGefi2DMPTfTL5SLmv7DivfNa, which is Satoshi Nakamoto's address from the Genesis Block.
[17]
This transaction,
77822fd6663c665104119cb7635352756dfc50da76a92d417ec1a12c518fad69
has an unusual scriptPubKey:
OP_IF OP_INVALIDOPCODE 4effffffff 1443 bytes of data OP_ENDIF.
[18] The encrypted GPG files are in transactions 7379ab5047b143c0b6cfe5d8d79ad240b4b4f8cced55aa26f86d1d3d370c0d4c#o448, d3c1cb2cdbf07c25e3c5f513de5ee36081a7c590e621f1f1eab62e8d4b50b635#o448, and cce82f3bde0537f82a55f3b8458cb50d632977f85c81dad3e1983a3348638f5c.
[19]
To "follow the money", the PDF transaction put change into address
1HT8vpTV1wj2ck6jgW7my6vCtJQv14Cdp. This address funded the embedding of a 10KB mystery file in this transaction. The change from that was used for another file
here, followed by this,
this,
and this.
These uploaded file transactions all included 0.001 BTC donations to 1JVQw1siukrxGFTZykXFDtcf6SExJVuTVE, the 50BTC.com address.
[20] Some addresses associated with the mystery transactions are: 18qr2srETSvQq4kP7yBYRqQ4LzmjhtRmcD, 1MaZAHzEFfinRJ2dwK6YtNDfvWMBkiAxDr, 1AgwESN7RKNZtaqzbqu6kPg3RS6C2qCgHi, 1AZUPm5PC5QguquNsBg7HhWUYz5dfm2nU9, and 1J1aR7ayNp9sma8QVyyWGF87PzDU1vp5BD.
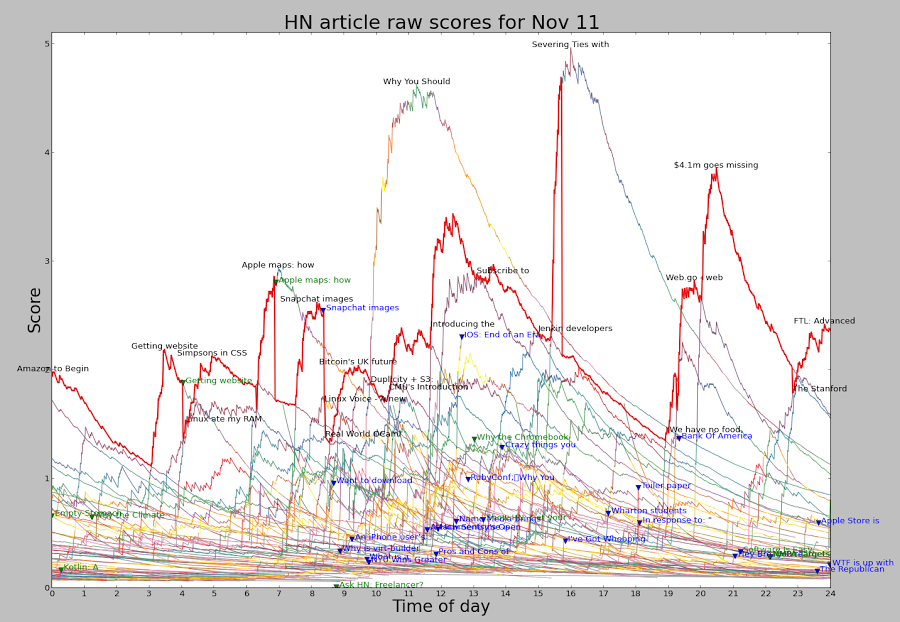
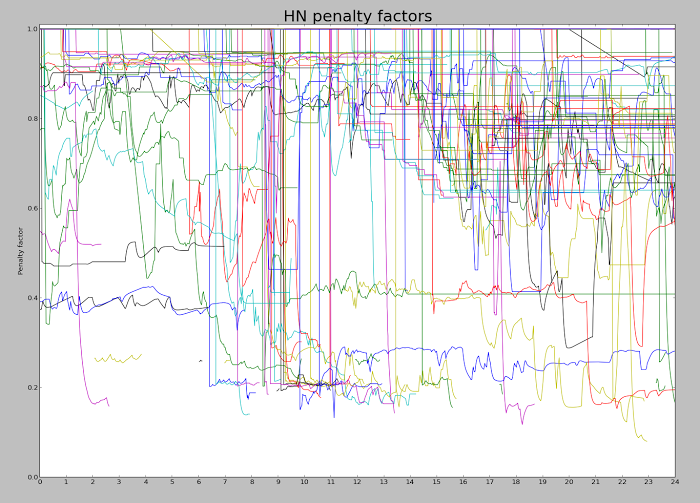
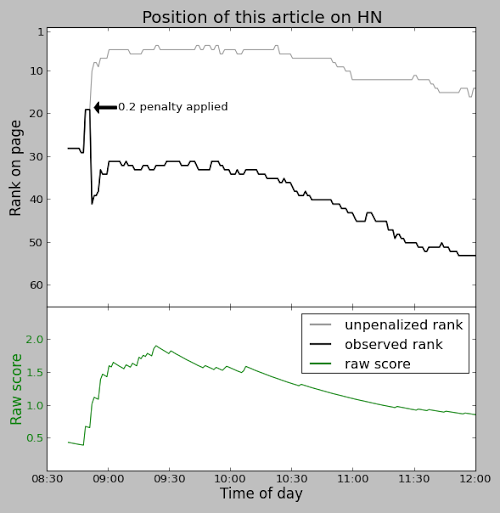
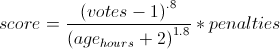Because the time has a larger exponent than the votes, an article's score will eventually drop to zero, so nothing stays on the front page too long. This exponent is known as gravity.
You might expect that every time you visit Hacker News, the stories are scored by the above formula and sorted to determine their rankings. But for efficiency, stories are individually reranked only occasionally. When a story is upvoted, it is reranked and moved up or down the list to its appropriate spot, leaving the other stories unchanged. Thus, the amount of reranking is significantly reduced. There is, however, the possibility that a story stops getting votes and ends up stuck in a high position. To avoid this, every 30 seconds one of the top 50 stories is randomly selected and reranked. The consequence is that a story may be "wrongly" ranked for many minutes if it isn't getting votes.
In addition, pages can be cached for 90 seconds.
