Bitcoin mining on an Apollo Guidance Computer: 10.3 seconds per hash

We've been restoring an Apollo Guidance Computer1. Now that we have the world's only working AGC, I decided to write some code for it. Trying to mine Bitcoin on this 1960s computer seemed both pointless and anachronistic, so I had to give it a shot. Implementing the Bitcoin hash algorithm in assembly code on this 15-bit computer was challenging, but I got it to work. Unfortunately, the computer is so slow that it would take about a million times the age of the universe to successfully mine a Bitcoin block.

The Apollo Guidance Computer powered up. The cover is off, showing the computer's purple wire-wrap wiring of the backplane. We built the interfaces that are plugged into the front of the computer. At the back, vintage core rope simulator boxes are visible in the core rope slots.

The Apollo Guidance Computer was developed in the 1960s for the Apollo missions to the Moon. Onboard the Apollo spacecraft, these computers provided guidance, navigation, and controlled the engines. In an era when most computers ranged from refrigerator-sized to room-sized, the Apollo Guidance Computer was small enough to fly in space. One of the very first computers to use integrated circuits, the AGC was 70 pounds and under a cubic foot in size.

The output from the Bitcoin mining program, displayed on the Display/Keyboard (DSKY). The display shows part of the Bitcoin hash in octal. The DSKY is a modern replica, hooked up to the genuine AGC.

The Apollo Guidance Computer also pushed the boundaries of software engineering under the leadership of Margaret Hamilton. It had a cutting-edge real-time operating system that supported multiple prioritized jobs2 along with fault detection and handling. Much of the software was in assembly language but the AGC also had an interpreter designed for navigation algorithms. The interpreter implemented a virtual machine that provided vector and matrix arithmetic along with trigonometry and double- and triple-precision numbers.

How Bitcoin mining works

As the leading digital currency, Bitcoin has received a lot of attention in the past few years. The Bitcoin system can be thought of as a ledger that keeps track of who owns which Bitcoins, and allows them to be transferred from one person to another. The revolutionary feature of Bitcoin is there's no central machine or authority keeping track of things. Instead, the records are spread across thousands of machines on the Internet, and the system works with nobody in charge.

To ensure everyone agrees on which transactions are valid, Bitcoin uses a process called mining—about every 10 minutes a block of outstanding transactions is mined, which makes the block "official". Bitcoin mining is designed so it takes an insanely huge amount of computational effort to mine a block, so nobody can take over the mining process. Miners compete against each other, generating trillions and trillions of random "hashes" until someone finds a lucky one that starts with 18 zeros.3 This hash forms a successfully mined block, and then everyone moves on to the next block. The idea is that getting 18 zeros in a row randomly is extremely unlikely, so it takes a huge number of tries before someone succeeds. It's kind of like a lottery, where miners keep trying until someone "wins", but finding a valid hash is less likely than finding a single grain of sand out of all the sand on Earth.

Each time a block is successfully mined, new Bitcoins are created; currently, a successful miner gets 12.5 new Bitcoins (worth $140,000) as well as transaction fees. The possibility of receiving $140,000 every 10 minutes motivates miners to build datacenters full of specialized hardware using huge amounts of electricity.4

Structure of a Bitcoin block. The data in yellow is hashed to yield the block hash, which becomes the identifier for the block. The block is linked to the previous block by including the previous block's hash, forming the blockchain. The Merkle root is a hash of all the transactions in the block.

The diagram above shows what actually goes into a block that is mined. The yellow part is the block header (which gets hashed), and it is followed by the transactions that go into the block. Each block contains the hash of the previous block, causing all the blocks to be linked together forming the blockchain. On the right, you can see that the hash above was successful because it starts with lots of zeros.

To summarize the mining process: you collect new Bitcoin transactions and create a header as in the diagram above. You generate the cryptographic hash of the block. If by some incredible chance the result starts with 18 zeros you send the block into the Bitcoin network and "win" $140,000 in Bitcoin. Otherwise, you change the header slightly and try again as fast as possible. When someone else succeeds in mining the block, you start over from the new block and new transactions.5

The SHA-256 hash algorithm used by Bitcoin

Where do these hashes come from? Bitcoin mining is based on cryptography, with a "hash function" that converts a block of data into an essentially random hash value. The hash algorithm is designed to be simple to implement, but cryptographically secure: there's no known short cut to finding a successful hash other than trying zillions of hashes through brute force. In particular, Bitcoin uses a standard cryptographic hash function called SHA-256.6 This algorithm is so simple you can literally do it by hand, but it manages to scramble the data entirely unpredictably.

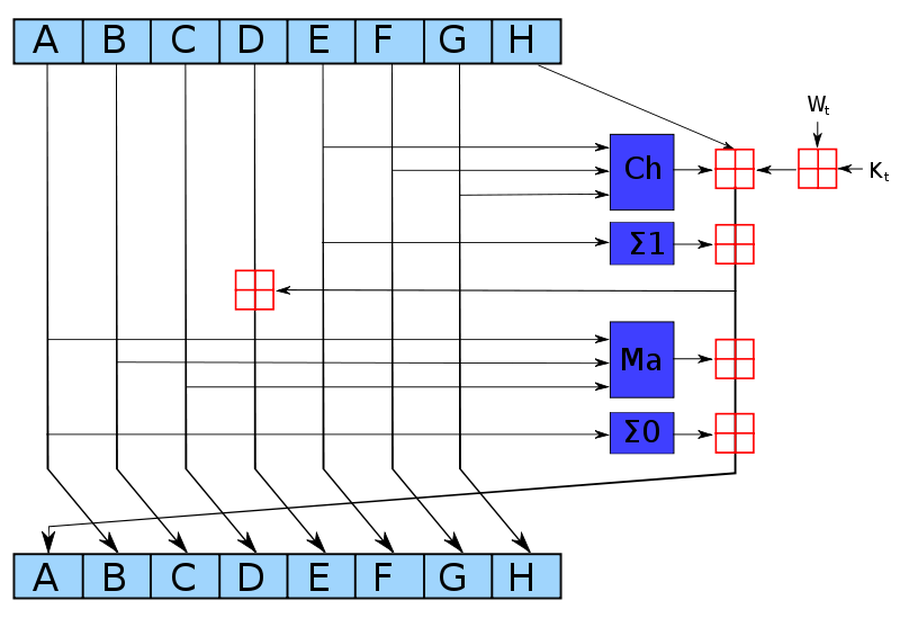
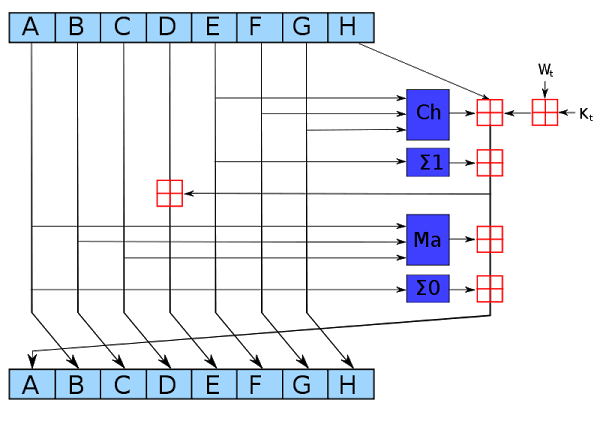
The SHA-256 algorithm can be described in about a page of pseudocode. It consists of a scrambling step called a "round", repeated 64 times. The diagram below shows one round, which takes eight 4-byte hash values, A through H, performs a few operations, and generates new values for A through H. As can be seen from the diagram, only A and E are changed in a round, while the others are just shifted over. Even so, after 64 rounds the input data will be completely scrambled, generating the unpredictable hash output.

This diagram shows the computations during one round of SHA-256. This process is repeated 64 times. Source: Wikipedia created by kockmeyer, CC BY-SA 3.0.

The operations in SHA-256 are simple bit operations. The red boxes above indicate 32-bit addition, generating new values for A and E. The Ch "choose" box chooses bits from F or G, based on the value of input E. The Σ "sum" boxes rotate and sum bits. The Ma "majority" box looks at the bits in each position of A, B, and C, and selects whichever value is in the majority. The K_t values are constants. The input data enters the algorithm through the W_t values. These operations can be easily implemented on a computer using simple arithmetic and logic operations.7 (The operations can also be easily implemented in a custom logic circuit, which is why Bitcoin mining chips are popular.)

The Apollo Guidance Computer's processor

The AGC doesn't have a microprocessor, as it was built years before microprocessors were developed. Instead, the processor is built from about 5600 NOR gates. These gates were combined to make circuits such as flip flops for registers, binary adders, control logic, and so forth. The AGC was one of the first computers to use integrated circuits; each integrated circuit held two NOR gates. The computer had 24 logic modules similar to the one below. Each logic module had 120 integrated circuits (240 NOR gates). For example, the registers and ALU were implemented with four modules, each implementing 4 bits of the processor.

A logic module from the Apollo Guidance Computer. The module consists of 120 integrated circuits, each one implementing two NOR gates. Photo courtesy of Mike Stewart.

The computer's architecture was unusual by modern standards: it used a 15-bit word, along with parity. (Back then, computers often had a word size that fit the application, not necessarily a power of 2.) The AGC had just 2K words of RAM, along with 36K words of ROM. Its ROM was constructed from core rope memory. (I wrote about the AGC's RAM core memory here and core rope here).

The Apollo Guidance Computer was slow even by 1960s standards; it could perform about 40,000 additions per second. (In the AGC's defense, this was an era when most computers ranged from refrigerator-sized to room-filling, so the AGC did well for its size.) The AGC's main strength was I/O: it had hundreds of I/O connections to provide real-time control of the spacecraft.

Implementing SHA-256 on the Apollo Guidance Computer

My implementation of the SHA-256 hash algorithm implementation follows the pseudocode pretty closely. I ran into some difficulties, though, since the AGC's instruction set lacks many features of modern computers. For instance, the AGC (like many 1960s computers) didn't have a stack, so you had to keep track of the return address for each subroutine call.

Another complication was that the SHA-256 algorithm uses 32-bit unsigned numbers, while the AGC used 15-bit signed numbers in obsolete 1's complement form, so even addition required some tricky code. To fit a 32-bit number into the AGC, I split each word into a 4-bit chunk and two 14-bit chunks. (I used 14-bit chunks and not 15-bit chunks because I needed to use unsigned arithmetic.)

The next issue was that the AGC has very limited memory. The AGC, like most computers of the 1960s, used magnetic core memory, storing each bit in a tiny magnetized ferrite ring. Since core memory was fairly bulky, the AGC had just 2K words (approximately 4K bytes) of RAM. The AGC's addressing scheme made things more complicated since you could only access 256 words unless you used an inconvenient bank switching mechanism. The problem is that the SHA-256 algorithm uses eight (32-bit) hash values, a 64-word message table, and 8 words of intermediate values. These three arrays alone used up 240 AGC words, leaving about 16 words for everything else (temporary values, subroutine return addresses, loop counters, pointers, etc.) I managed to get everything to fit in one bank by reusing these 16 words for multiple purposes, but I spent a lot of time debugging problems when a variable clobbered a location still in use.

For RAM, the Apollo Guidance Computer used this 2 kiloword core memory module.

Most modern computers have shift and rotate instructions to manipulate words, but the AGC instead used three special registers. Writing to a special register would cycle the value right one bit, shift the value right, or cycle the value left. The SHA-256 algorithm uses many 32-bit shifts and rotates, which I had to convert into loops using the 15-bit cycle register. The point is that a shift operation like x>>10 is trivial in C, but I needed to implement a whole subroutine to do it on the AGC.

Our Apollo Guidance Computer and replica DSKY. The computer's I/O connectors are visible at the front of the computer. six core rope slots at the back are empty. The photo is an homage to this classic AGC photo.

To keep the instruction set and code size small, the AGC had some instructions with side effects you wouldn't expect. For example, the TS (Transfer to Storage) instruction wrote a value to memory, which seems straightforward. But if the previous addition had an overflow (i.e. a carry), TS also skipped the next instruction and loaded the accumulator with a +1 or -1. In other words, simply writing a value to memory could result in a jump in control flow and register modification. The purpose of this was to handle carries for multiple-precision arithmetic, but most computers simply implement this with an "Add with carry" instruction.

Running the program

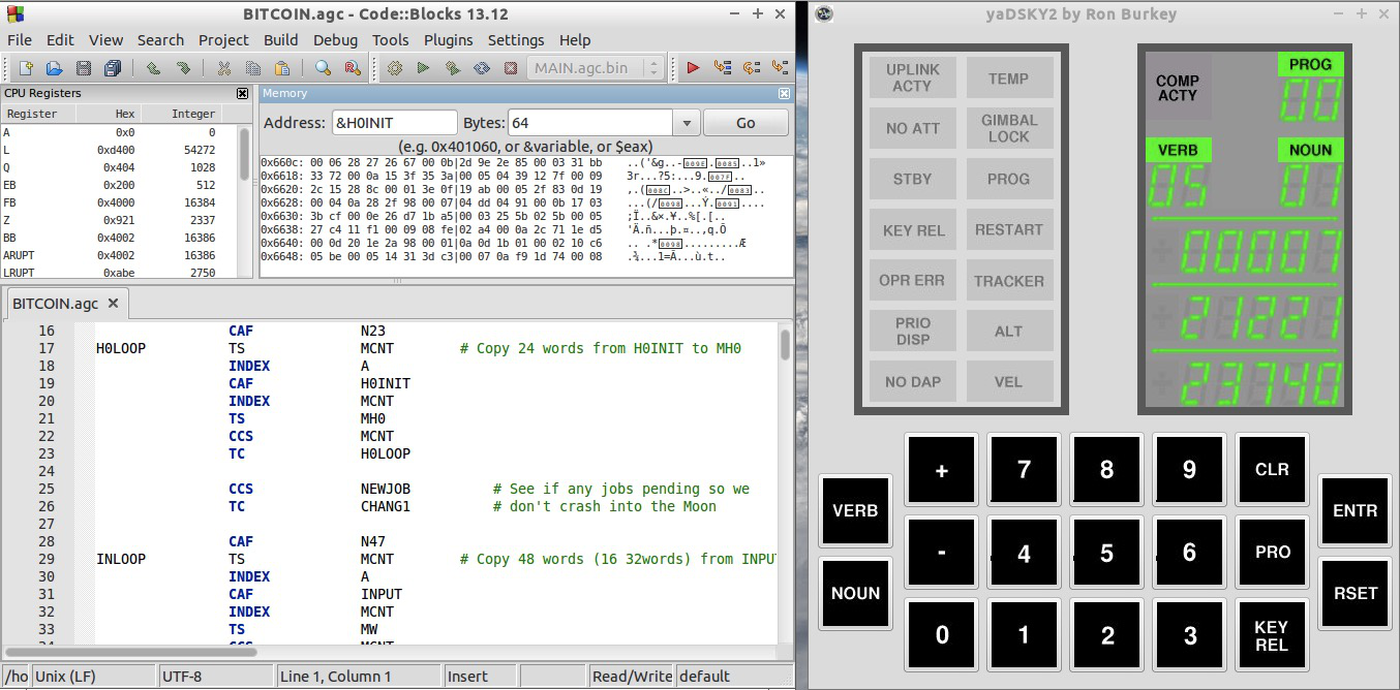
The video below shows my Bitcoin program running on an actual Apollo Guidance Computer with the results displayed on our DSKY (Display/Keyboard). The DSKY had a simple numeric keypad with buttons large enough for astronauts to use with gloves on. The computer displayed output numerically; astronauts had to know if the output was feet, seconds, degrees, or something else. We used a replica DSKY created by Carl since nobody would let us use a real DSKY.8

The Apollo Guidance Computer had a very simple user interface through the DSKY. An astronaut selected an action pressing the "Verb" key, entering a verb number, and pressing "Enter". The astronaut selected a target for the action by entering a "Noun". (Astronauts had a reference card listing all the verbs and nouns.) I added Bitcoin mining as Verb 65 in a program called Borealis9; you can see Mike enter Verb 65 at the beginning of the video.

The Apollo Guidance Computer took 5.15 seconds for one SHA-256 hash. Since Bitcoin uses a double-hash, this results in a hash rate of 10.3 seconds per Bitcoin hash. Currently, the Bitcoin network is performing about 65 EH/s (65 quintillion hashes per second). At this difficulty, it would take the AGC 4×10^23 seconds on average to find a block. Since the universe is only 4.3×10^17 seconds old, it would take the AGC about a million times the age of the universe to successfully mine a block.

Given the astronomical difficulty of mining, you might wonder how I successfully mined a block. For this demonstration, I simply used as input a block that had been successfully mined in the past, specifically block #286819. Thus, the algorithm succeeded quickly, but since it was an old block, I didn't make any money off it.

To put the AGC's mining performance in perspective, a USB stick miner performs 130 billion hashes per second. The stick miner costs under $70, compared to $150,000 for the Apollo Guidance Computer. For its time, the Apollo Guidance Computer was an extremely compact, low-power system, using 55 watts and taking up under a cubic foot of space. The USB miner, though, uses 12 watts and fits in your hand. The enormous difference in performance is due to the exponential increase in computer speed described by Moore's law as well as the advantage of custom Bitcoin mining hardware.

Programming the AGC—then and now

In the 1960s, code for the AGC was written on punch cards, and assembled onto tape using a software system called YUL. This system was more advanced than you'd expect for the 1960s, including a source control system to track and incorporate changes. For flight, the software was woven into core ropes, with wires physically going around cores for a 0 or through cores for a 1. In other words, each core rope was custom-manufactured, with the data stored in the weaving pattern of the wires. This provided high-density, reliable ROM storage, but required weeks of manufacturing.

Detail of core rope memory wiring from an early (Block I) Apollo Guidance Computer. Photo from Raytheon.

Since it wasn't practical to manufacture a new core rope for every change, a different approach was used during development. A core rope simulator allowed a program to be fed into the AGC from external storage. This simulator was part of the refrigerator-sized monitor (below), which provided a debugging interface to the AGC through a test connector on the AGC. The monitor allowed programmers to set breakpoints, single-step, examine registers, and so forth, using lights and switches.

The AGC monitor provided a debugging interface to the AGC as well as a core rope simulator. See User's guide to the AGC monitor.

In my case, I wrote the software on my laptop and assembled it with yaYUL, a modern version of YUL written by the Virtual AGC team. I tested the software on a simulated AGC using the Code::Blocks IDE11, which provides debugging features somewhat similar to what the monitor provided in the 1960s. To run the code on the real AGC, we obviously didn't manufacture core ropes. We have vintage core rope simulator boxes, but they turned out to be extremely unreliable. Fortunately, Mike Stewart built a board to load code into the AGC using the same AGC test connector originally used by the monitor.

AGC code can be developed in an IDE. The debugger makes it much easier to develop code. The IDE communicates with the virtual DSKY.

Conclusion

I implemented the SHA-256 hash algorithm and ran it on the Apollo Guidance Computer that we're restoring, taking 10.3 seconds per hash. This isn't my first experiment with absurd Bitcoin mining. I tried mining by hand with pencil and paper; this had a hash rate of 0.67 hashes per day. Using an IBM punch card mainframe computer from the early 1960s got the hash rate up to 80 seconds per hash. My fastest implementation was on a Xerox Alto (the famous 1973 computer that inspired the Macintosh), which performed 1.5 hashes per second. Thus, the Apollo Guidance Computer outperformed the older transistor-based IBM computer but not the Alto.

My Bitcoin mining experiments by hand, on a punch-card mainframe, and on a Xerox Alto.

The Apollo program cost 25.4 billion dollars as of 1973, equivalent to about 150 billion dollars today. The current market cap of Bitcoin is 200 billion dollars, so if NASA had been mining Bitcoins, they could have paid for the whole Apollo program and still had money left over. One flaw in this plan is the Apollo Guidance Computer's low performance, since mining a block would take much more than the lifetime of the universe.

My code is available on Github; the mining code is in BITCOIN.agc. CuriousMarc has a series of AGC videos which you should watch for more information on the restoration project. I announce my latest blog posts on Twitter, so follow me @kenshirriff for future articles. I also have an RSS feed. Thanks to Mike Stewart for supplying images and extensive information.

Notes and references

1. The AGC restoration team consists of Mike Stewart (creator of FPGA AGC), Carl Claunch, Marc Verdiell (CuriousMarc on YouTube) and myself. The AGC that we're restoring belongs to a private owner who picked it up at a scrap yard in the 1970s after NASA scrapped it. For simplicity, I refer to the AGC we're restoring as "our AGC".

   The Apollo flights had one AGC in the command module (the capsule that returned to Earth) and one AGC in the lunar module. In 1968, before the Moon missions, NASA tested a lunar module with astronauts aboard in a giant vacuum chamber in Houston to ensure that everything worked in space-like conditions. We believe our AGC was installed in that lunar module (LTA-8). Since this AGC was never flown, most of the modules were not potted with epoxy. ↩

2. Because the AGC supported multiple programs at once, my code needed to periodically call NEWJOB to see if there were any other waiting jobs to run. To ensure reliability, the AGC constantly checked to make sure a faulty program doesn't take over the system. Thus, I needed to give other jobs the chance to run or else my job would get killed. ↩

3. At the current Bitcoin difficulty level, about 1 in 10^22 hashes will be successful at mining a block; a valid hash must start with approximately 18 zeros. The mining difficulty changes periodically to keep the time between blocks at approximately 10 minutes. As mining hardware gets faster, the difficulty factor is automatically updated to make mining more difficult so miners can never really catch up. ↩

4. A while back I estimated that Bitcoin mining uses about as much electricity as the entire country of Cambodia. One paper puts mining's energy consumption comparable to Ireland's electricity usage. A recent estimate is that Bitcoin mining uses more electricity than Switzerland. ↩

5. I've simplified a lot of details in my discussion of Bitcoin algorithms. For in-depth information on Bitcoin and mining, see my articles Bitcoins the hard way and Bitcoin mining the hard way. ↩

6. Bitcoin uses "double SHA-256" which simply consists of applying the SHA-256 function twice. I could have implemented the double-hash in the AGC code, but I ran out of time; I got the basic hash working at 4 am the night before we sent the AGC back to Houston. How to upload transactions into the AGC is also left as an exercise for the reader. ↩

7. While SHA-256 is easy to implement, that's not the case for all the cryptography used by Bitcoin. To create a Bitcoin transaction, the transaction must be signed with elliptic curve cryptography. This requires 256-bit modular arithmetic, which is about as hard as it sounds. Even a simple implementation is 1000 lines of C. Needless to say, I decided not to implement signing in assembly language on the AGC. ↩

8. Many people have asked if we talked to Fran Blanche about the DSKY. Yes, we have. ↩

9. The Aurora program was used to extensively test the operation of the Apollo Guidance Computer in the Lunar Module. I wrote the Bitcoin code as part of Borealis, a modern version of Aurora slightly cleaned up. The code for Aurora and Borealis includes a table of verb definitions so it was straightforward for me to add Verb 65 for my Bitcoin code. In the video, you can see Mike enter Verb 65 to start the Bitcoin program. I also took advantage of the Executive's octal display routine to show the output. This routine is accessed through Verb 05 Noun 01, which is why you'll see that on the display at the end of the video. ↩

10. At the end of the video clip, the display shows 8 octal triples indicating the hash: 00000/00000/00000, 00000/00000/00000, 00007/21221/23740, 00017/35565/05002, 00002/20333/04715, 0o00002, 0o33226, 0o05227, 00004/05367/35221, 00005/00252/14222. (The 11111/11111/11111 value is just a signal that all values have been displayed.) Converting these to hex and reversing the bytes yields the 8-byte Bitcoin hash: 00000000 00000000 e067a478 024addfe cdc93628 978aa52d 91fabd42 92982a50. Note the multiple zeros at the beginning of the hash; this is what makes the hash valid. ↩

11. The Virtual AGC project has developed simulations of the AGC, DSKY, and YUL assembler, so you can experiment with the AGC system. While you can do this from the command line, debugging is much, much easier if you use the Code::Blocks IDE. You can download a VirtualBox environment with everything set up here. In the folder "AGC Visual Debugging", double-click on Borealis to start Code::Blocks. You can edit code in the IDE (or with an editor). Then "Build → Build" compiles the code and "Debug → Start" runs code in the debugger. "Tools → DSKY" starts up a DSKY window to interact with the AGC. "Debug → Debugging windows → Memory dump" lets you look at memory contents. The IDE lets you set breakpoints, single-step through code, examine memory, and so forth. For more information on AGC code development, see this page. ↩

12. The Bitcoin protocol is a mish-mash of big-endian and little-endian values. It inconveniently reverses the byte order of the SHA-256 hash, so while the hash from the algorithm ends with zeros, the Bitcoin hash starts with zeros. I displayed the hash to match the Bitcoin order. ↩

Bitcoin mining on a vintage Xerox Alto: very slow at 1.5 hashes/second

I've been restoring a Xerox Alto minicomputer from the 1970s and figured it would be interesting to see if it could mine bitcoins. I coded up the necessary hash algorithm in BCPL (the old programming language used by the Alto) and found that although the mining algorithm ran, the Alto was so slow that it would take many times the lifetime of the universe to successfully mine bitcoins.

Bitcoin mining on a vintage Xerox Alto computer.

The Alto was a revolutionary computer designed at Xerox PARC in 1973 to investigate personal computing. It introduced high-resolution bitmapped displays, the GUI, Ethernet and laser printers to the world, among other things. In the photo above, the Alto computer is in the lower cabinet. The black box is the 2.5 megabyte disk drive. The Alto's unusual portrait display and an early optical mouse are on top.

How Bitcoin mining works

Bitcoin, a digital currency that can be transmitted across the Internet, has attracted a lot of attention lately. The Bitcoin system can be thought of as a ledger that keeps track of who owns which bitcoins, and allows them to be transferred from one person to another. The revolutionary feature of Bitcoin is there's no central machine or authority keeping track of things. Instead, the "blockchain" is stored across thousands of machines on the Internet, and the system works with nobody in charge.

To ensure everyone agrees on which transactions are valid, Bitcoin uses a process called mining—about every 10 minutes a block of outstanding transactions is mined, which makes the block "official". Bitcoin mining is designed to take an insanely huge amount of computational effort to mine a block, so nobody can take over the mining process. Miners compete against each other, generating trillions and trillions of "hashes" until someone finds a lucky one that succeeds in mining a block. It's hard to visualize just how difficult the hashing process is: finding a valid hash is less likely than finding a single grain of sand out of all the sand on Earth.

Bitcoin mining is based on cryptography, with a "hash function" that converts a block into an essentially random hash value. If the hash starts with 17 zeros,1 the block is successfully mined and is sent into the Bitcoin network. Most of the time the hash isn't successful, so the miner will modify the block slightly and try again, over and over billions of times. About every 10 minutes someone will successfully mine a block, and the process starts over. It's kind of like a lottery, where miners keep trying until someone "wins".

As a side-effect, mining adds new bitcoins to the system. For each block mined, miners currently get 12.5 new bitcoins (currently worth about $30,000) as well as fees, which encourages miners to do the hard work of mining blocks. With the possibility of receiving $30,000 every 10 minutes, miners invest in datacenters full of specialized mining hardware using huge amounts of electricity2.

Structure of a Bitcoin block. The data in yellow is hashed to yield the block hash, which becomes the identifier for the block. The block is linked to the previous block by including the previous block's hash, forming the blockchain. The Merkle root is a hash of all the transactions in the block.

The diagram above shows what actually goes into a block that is mined. The yellow part is the block header (which gets hashed), and it is followed by the transactions that go into the block. Each block contains the hash of the previous block, causing all the blocks to be linked together forming the blockchain. You can see that for the block above, the hash is successful because it starts with lots of zeros: 0000000000000000e067a478024addfecdc93628978aa52d91fabd4292982a50. The "Merkle root" is a hash of all the transactions that go into the block; this ensures that none of the mined transactions can be changed. The nonce is an arbitrary number; each attempt at mining the block changes the nonce.

To summarize the mining process: you collect new Bitcoin transactions and create a header (as in the diagram above). You do the cryptographic hash of the block. If by some incredible chance the result starts with 17 zeros you send the block into the Bitcoin network and "win" $30,000 in bitcoin. Otherwise, you change the nonce and try again. Probably none of the nonce values will work, so you change something else in the header and start over. If someone else succeeds in mining the block, you start over with the new previous block hash and new transactions.

I've simplified a lot of details above. For in-depth information on Bitcoin and mining, see my articles Bitcoins the hard way and Bitcoin mining the hard way.

The SHA-256 hash algorithm used by Bitcoin

Next, I'll discuss the hash function used in Bitcoin, which is based on a standard cryptographic hash function called SHA-256.3 The SHA-256 algorithm is so simple you can literally do it by hand, but it manages to scramble the data entirely unpredictably. The SHA-256 hash algorithm takes input blocks of 512 bits (i.e. 64 bytes), combines the data cryptographically, and generates a 256-bit (32 byte) output.

The SHA-256 algorithm consists of a simple round repeated 64 times. The diagram below shows one round, which takes eight 4-byte inputs, A through H, performs a few operations, and generates new values for A through H. As can be seen from the diagram above, only A and E are changed in a round, while the others are just shifted over. Even so, after 64 rounds the input data will be completely scrambled, generating the unpredictable hash output.

The SHA-256 algorithm is pretty simple, about a page of pseudocode and can be easily implemented on a computer, even one as old as the Alto, using simple arithmetic and logic operations.5

SHA-256 round, from Wikipedia created by kockmeyer, CC BY-SA 3.0.

The dark blue boxes mix up the values in non-linear ways that are hard to analyze cryptographically. (If you could figure out a mathematical shortcut to generate successful hashes, you could take over Bitcoin mining.) The Ch "choose" box chooses bits from F or G, based on the value of input E. The Σ "sum" boxes rotate the bits of A (or E) to form three rotated versions, and then sum them together. The Ma "majority" box looks at the bits in each position of A, B, and C, and selects 0 or 1, whichever value is in the majority. The red boxes perform 32-bit addition, generating new values for A and E. The input data enters the algorithm through the W_t values. The K_t values are constants defined for each round.4

Implementing SHA-256 in BCPL

I implemented SHA-256 in BCPL, a programming language that was a precursor to C. It's a lot like C with syntax changes, except the only type is 16-bit words. My SHA-256 code is in sha256.bcpl. The snippet below (the choose function) will give you an idea of what BCPL looks like. Each value is two words; BCPL does array access with !1 instead of [1]. Like C++, comments are indicated with a double slash. Unlike C, BCPL uses words for xor and not.

   // ch := (e and f) xor ((not e) and g)
   ch!0 = (e!0 & f!0) xor ((not e!0) & g!0)
   ch!1 = (e!1 & f!1) xor ((not e!1) & g!1)

The mining is done in bitcoin.bcpl: it creates a Bitcoin header (from hardcoded values), substitutes the nonce, and calls the SHA-256 code to hash the header twice. One interesting feature of the code is the structure definition for the Bitcoin header in BCPL (below), similar to a C struct. It defines a two word field for version, 16 words for prevHash, and so forth; compare with the Bitcoin structure diagram earlier. Interestingly, ^1,16 indicates an array with indices from 1 to 16 inclusive. BCPL is not 0-indexed or 1-indexed, but lets you start array indices at arbitrary values.7

structure HEADER:
[
version^1,2 word
prevHash^1,16 word
merkleRoot^1,16 word
timestamp^1,2 word
bits^1,2 word
nonce^1,2 word
]

The line shows how structures are accessed in BCPL; it initializes one word of the header, using the slightly strange BCPL syntax. >>HEADER sort of casts the header variable to the HEADER structure described earlier. Then .prevhash^1 accesses the first word of the prevhash field. Also note that #13627 is an octal value; BCPL inconveniently doesn't include hex constants.6

header>>HEADER.prevHash^1 = #13627

The screenshot below shows the output as the program runs. The number on the left is each nonce in sequence as it is tested. The long hex number on the right is the resulting hash value. Each nonce results in a totally different hash value, due to the cryptographic hash algorithm.

On the Alto screen, each line shows a nonce value and the resulting hash.

Performance

The Alto can hash about 1.5 blocks per second, which is exceedingly slow by Bitcoin standards. At this speed, mining a single block on the Alto would take about 5000 times the age of the universe The electricity would cost about 2x10^16 dollars. And you'd get 12.5 bitcoins (₿12.5) worth about $30,000. Obviously, mining Bitcoin on a Xerox Alto isn't a profitable venture.

In comparison, a USB stick miner performs 3.6 billion hashes per second. The Alto cost about $12,000 to manufacture in 1973 (about $60,000 in current dollars), while the stick miner costs $200. The Alto used hundreds of watts, while the stick minter uses about 4 watts. The enormous difference in performance is due to huge increase in computer speed since the 1970s described by Moore's law as well as the giant speed gain from custom Bitcoin mining hardware.

The Alto wasn't a particularly fast machine, performing about 400,000 instructions per second. The Alto's instruction set lacks many of the operations you'd find on a modern processor. For instance, the SHA-256 algorithm makes heavy use of Boolean operations including exclusive-OR and OR. These are pretty basic instructions that you'd find on even something as primitive as the 6502, but the Alto doesn't have them. Instead, these operations are implemented with an inefficient subroutine call that does a sequence of operations with the same effect.

In addition, SHA-256 heavily uses bit shift and rotate operations. Modern processors typically have a "barrel shifter" that lets you shift by as many bits as you want in one step. The Alto's shift instructions, on the other hand, only shift a single bit. Thus, to shift by, say 10 bits, the Alto code calls a subroutine that performs 10 separate shift instructions. The result is a shift operation is much slower than you might expect.

You can see the Alto's arithmetic-logic board below. The Alto didn't use a microprocessor but instead built a CPU from simple TTL chips. You can see that even providing single-bit shifts required 8 separate chips—it's not surprising that the Alto doesn't do more complex shift operations.

The Alto doesn't have a microprocessor, but a CPU built from individual TTL chips. The ALU board has chips for arithmetic, chips for shifting, and chips for registers.

I should point out that I'm not trying to write the best possible mining code for the Alto, and there are plenty of optimizations that one could do.8 For instance, writing the code in microcode would speed it up considerably, but Alto microcode is very hard to understand, let along write. My blog post on generating the Mandelbrot set on the Alto discussed Alto performance optimizations in detail, so I won't say more about optimization here.

Conclusion

The screenshot below shows a successful hash, ending in a bunch of zeros9. (I also display an image to show off the Alto's high-resolution bitmapped display.) Since the Alto would take well beyond the lifetime of the universe to find a successful hash, you might wonder how I found this. For this demonstration I simply used as input a block that had been successfully mined in the past, specifically block #286819. Thus, the algorithm succeeded quickly, but since it was an old block, I didn't make any money off it.

The algorithm found a successful hash, indicated by all the zeros at the end. Bitcoin graphic source probably MoneyWeek.

My code is on github if you want to look at BCPL code or try it out.

Notes and references

1. At current difficulty, about 1 in 3x10^21 hashes will be successful at mining a block; a valid hash must start with approximately 17 zeros. The mining difficulty changes periodically to keep the time between blocks at approximately 10 minutes. As mining hardware gets faster, the difficulty factor is automatically updated to make mining more difficult so miners can never really catch up. ↩

2. A while back I estimated that Bitcoin mining uses about as much electricity as the entire country of Cambodia. One paper puts mining's energy consumption comparable to Ireland's electricity usage. ↩

3. Bitcoin uses "double SHA-256" which simply consists of applying the SHA-256 function twice.  ↩

4. The K constants used in the SHA-256 algorithm are provided by the NSA. You might worry that the NSA cleverly designed these constants to provide a backdoor. However, to prove that these are just arbitrary random constants, the NSA simply used the cube roots of the first 64 primes. ↩

5. While SHA-256 is easy to implement, that's not the case for all the cryptography used by Bitcoin. To create a Bitcoin transaction, the transaction must be signed with elliptic curve cryptography. This requires 256-bit modular arithmetic, which is about as hard as it sounds. Even a simple implementation is 1000 lines of C. I decided that porting this to BCPL was too much effort for me. ↩

6. I wrote a simple Python script to convert the many 32-bit hexadecimal constants used by SHA-256 to 16-bit octal constants. It's a good thing that hex has almost entirely replaced octal, as it is much better. ↩

7. Some people claim that BCPL arrays are 0-based. However, arrays in BCPL structures can start at an arbitrary value. I start with 1 because that's what the Alto code typically does. (This caused me no end of confusion until I realized the indices weren't zero-based.) ↩

8. The code could be made 33% faster by taking advantage of an interaction between SHA-256 and the Bitcoin header structure. Bitcoin performs a SHA-256 hash twice on the 80-byte header. Since SHA-256 only handles 64 bytes at a time, the first hash requires two SHA-256 cycles. The second hash takes a third SHA-256 cycle. However, when mining, the only thing that changes from one attempt to the next is the nonce value in the header. It happens to be in the second half of the header, which means the SHA-256 cycle performed on the first half of the header can be done once and then reused. Thus, the double SHA-256 hash can be done with two SHA-256 cycles instead of three. Bitcoin mining usually performs this optimization, but I left it out of the code to make the code less confusing. ↩

9. You might wonder why Bitcoin successful hashes start with a bunch of zeros, while the displayed hash ends with a bunch of zeros. The reason is that Bitcoin reverses the byte order of the SHA-256 output. If you look closely, you'll see that the displayed hash matches the hash in the Bitcoin block diagram if you reverse bytes (i.e. pairs of hex digits). ↩

How I added 6 characters to Unicode (and you can too)

Edit (June 2018): Unicode 11 is released, containing the half stars. Now the wait for font support...

Star characters (☆★) have long been part of the Unicode standard, which means they can appear as characters in web pages, text, and email. But half-stars were missing, so they required special images or custom fonts. I recently co-wrote a proposal to add half-star characters to Unicode, and it was just accepted. In an upcoming Unicode release, half-stars will be usable like any other text character. In this article, I discuss how I got the half-star characters and two others added to Unicode.

Usage of the four different half-stars to express 3.5 of 5.

Unicode is the computer standard that defines the characters that are used by almost every computer—this standard allows different computers to easily display text in almost every language, and with almost every symbol you might need. (Before Unicode, dealing with non-English text on computers was a mess.) But Unicode doesn't include everything. Last June, a comment on Hacker News complained that Unicode lacked the half-star character used in ratings and movie reviews:

Until Unicode has a half-star character, it won't even be able to encode the average newspaper.

I suggested that someone should propose the half-star to Unicode, but quickly realized that "someone" would be me. Since I had successfully proposed two symbols to Unicode earlier, I knew the process necessary to get the half-star added.

A few years ago, a detailed article described how a couple people got power symbols added to Unicode. Adding a new character to Unicode is easier than most people think. You don't need to pay money, be part of a major company or join a committee. All you need to do is write a proposal explaining why the character is needed. If the Unicode Committee agrees, they'll approve your character for addition to Unicode.

In 2015, I started programming the 1960s-era IBM 1401 mainframe at the Computer History Museum. But when I wrote about the IBM 1401 system, I ran into a problem. This computer uses a 6-bit character set (the precursor to EBCDIC) with some strange characters. All these characters appeared in Unicode, with the exception of one: the Group Mark. I was a bit shocked that Unicode, with its 128,172 characters, lacked a character I needed. Having read about the power symbol team's success in adding characters, I figured it would be interesting to see if I could get the group mark character added to Unicode. I wrote a proposal, submitted it to Unicode, and at the next meeting it was approved.

The group mark character, from an IBM 705 computer manual (1959). Since Unicode lacked this character, you couldn't write this text on a modern computer.

A few months later, I learned that the Bitcoin symbol was missing from Unicode. This was a surprising omission, since the Bitcoin symbol is widely used in the real world. The symbol had been rejected before, so I made a more thorough proposal in October 2015 with the enthusiastic support of /r/bitcoin and other Bitcoin groups. The Bitcoin symbol proposal was accepted by the Unicode Committee in November 2015.

The Bitcoin symbol on an IBM punched card. Mining Bitcoins on a punched card mainframe isn't practical, but was an interesting experiment.

So when I saw the comment about half-stars on Hacker News, I figured it would be straightforward to get it accepted to Unicode. I wrote a proposal after discussion on HN and on the Unicode mailing list. The Unicode committee considered the proposal in August 2016, but to my surprise they had also received another half star proposal, so they decided to wait on a single proposal. It turned out that Andrew West had also written a proposal for half-stars, and we had both submitted proposals, unaware of the other. So Andrew and I joined forces and made a combined proposal, which was accepted by the committee Sept 30, 2016.

Why did we propose four different half-stars? We included both the outline half-star and solid half-star because both forms are commonly used. (I wasn't sure if the committee would consider these characters distinct enough to include both, but they did.) Right-to-left languages such as Hebrew do their star ratings right-to-left too (which was a bit of a surprise to me), so we included mirrored versions for RTL languages. Thus, the four different half-stars cover the range of uses.

Half-stars in Hebrew are written right-to-left. From Haaretz 2 November 2012, provided by Simon Montagu.

If there's a character that you want to add to Unicode and it meets the requirements, you should submit a proposal, since its a very interesting process and not too difficult. Make sure your character meets the criteria. In particular, you'll need to find a bunch of examples of the character used in text. The Unicode Committee isn't going to add a character just because you think it's cool, so you need examples to prove the character is in use. Creating a font to demonstrate your new character is probably the most challenging part; I used FontForge. The power symbol team has lots of helpful advice on making a successful proposal. I'm also happy to offer advice if you're writing a proposal.

I should mention that emojis have a totally different process, so don't argue that "since the poop emoji exists, my character should too". (The poop emoji 💩 was added for backwards compatibility with Japanese mobile phones.) For emoji, expected popularity of the symbol is a major factor in acceptance. Regular Unicode, on the other hand, isn't concerned with popularity—historical scripts such as Tangut won't get a millionth the usage of a new emoji—but with existing usage in text. (Reading between the lines, I think a lot of the Unicode committee wishes they weren't in the emoji business at all.)

Once a character is accepted, there's still a long road for it to appear in fonts and be usable. A new version of Unicode is released typically every June, so the half stars will probably appear in Unicode 11.0 mid-2018. The Bitcoin community in particular has had to wait patiently since the Bitcoin symbol just missed the cutoff for Unicode 9.0, so it will probably appear in Unicode 10.0, mid-2017. So if you're patient, eventually you'll be able to use the group mark, Bitcoin symbol and half stars in web pages and text just like any other symbol.

Bitcoin mining on a 55 year old IBM 1401 mainframe: 80 seconds per hash

Could an IBM mainframe from the 1960s mine Bitcoin? The idea seemed crazy, so I decided to find out. I implemented the Bitcoin hash algorithm in assembly code for the IBM 1401 and tested it on a working vintage mainframe. It turns out that this computer could mine, but so slowly it would take more than the lifetime of the universe to successfully mine a block. While modern hardware can compute billions of hashes per second, the 1401 takes 80 seconds to compute a single hash. This illustrates the improvement of computer performance in the past decades, most famously described by Moore's Law.

The photo below shows the card deck I used, along with the output of my SHA-256 hash program as printed by the line printer. (The card on the front of the deck is just for decoration; it was a huge pain to punch.) Note that the second line of output ends with a bunch of zeros; this indicates a successful hash.

Card deck used to compute SHA-256 hashes on IBM 1401 mainframe. Behind the card deck is the line printer output showing the input to the algorithm and the resulting hash.

How Bitcoin mining works

Bitcoin, a digital currency that can be transmitted across the Internet, has attracted a lot of attention lately. If you're not familiar with how it works, the Bitcoin system can be thought of as a ledger that keeps track of who owns which bitcoins, and allows them to be transferred from one person to another. The interesting thing about Bitcoin is there's no central machine or authority keeping track of things. Instead, the records are spread across thousands of machines on the Internet.

The difficult problem with a distributed system like this is how to ensure everyone agrees on the records, so everyone agrees if a transaction is valid, even in the presence of malicious users and slow networks. The solution in Bitcoin is a process called mining—about every 10 minutes a block of outstanding transactions is mined, which makes the block official.

To prevent anyone from controlling which transactions are mined, the mining process is very difficult and competitive. In particular a key idea of Bitcoin is that mining is made very, very difficult, a technique called proof-of-work. It takes an insanely huge amount of computational effort to mine a block, but once a block has been mined, it is easy for peers on the network to verify that a block has been successfully mined. The difficulty of mining keeps anyone from maliciously taking over Bitcoin, and the ease of checking that a block has been mined lets users know which transactions are official.

As a side-effect, mining adds new bitcoins to the system. For each block mined, miners currently get 25 new bitcoins (currently worth about $6,000), which encourages miners to do the hard work of mining blocks. With the possibility of receiving $6,000 every 10 minutes, there is a lot of money in mining and people invest huge sums in mining hardware.

Line printer and IBM 1401 mainframe at the Computer History Museum. This is the computer I used to run my program. The console is in the upper left. Each of the dark rectangular panels on the computer is a "gate" that can be folded out for maintenance.

Mining requires a task that is very difficult to perform, but easy to verify. Bitcoin mining uses cryptography, with a hash function called double SHA-256. A hash takes a chunk of data as input and shrinks it down into a smaller hash value (in this case 256 bits). With a cryptographic hash, there's no way to get a hash value you want without trying a whole lot of inputs. But once you find an input that gives the value you want, it's easy for anyone to verify the hash. Thus, cryptographic hashing becomes a good way to implement the Bitcoin "proof-of-work".

In more detail, to mine a block, you first collect the new transactions into a block. Then you hash the block to form an (effectively random) block hash value. If the hash starts with 16 zeros, the block is successfully mined and is sent into the Bitcoin network. Most of the time the hash isn't successful, so you modify the block slightly and try again, over and over billions of times. About every 10 minutes someone will successfully mine a block, and the process starts over. It's kind of like a lottery, where miners keep trying until someone "wins". It's hard to visualize just how difficult the hashing process is: finding a valid hash is less likely than finding a single grain of sand out of all the sand on Earth. To find these hashes, miners have datacenters full of specialized hardware to do this mining.

I've simplified a lot of details. For in-depth information on Bitcoin and mining, see my articles Bitcoins the hard way and Bitcoin mining the hard way.

The SHA-256 hash algorithm used by Bitcoin

Next, I'll discuss the hash function used in Bitcoin, which is based on a standard cryptographic hash function called SHA-256. Bitcoin uses "double SHA-256" which simply applies the SHA-256 function twice. The SHA-256 algorithm is so simple you can literally do it by hand, but it manages to scramble the data entirely unpredictably. The algorithm takes input blocks of 64 bytes, combines the data cryptographically, and generates a 256-bit (32 byte) output. The algorithm uses a simple round and repeats it 64 times. The diagram below shows one round, which takes eight 4-byte inputs, A through H, performs a few operations, and generates new values for A through H.

SHA-256 round, from Wikipedia created by kockmeyer, CC BY-SA 3.0.

The dark blue boxes mix up the values in non-linear ways that are hard to analyze cryptographically. (If you could figure out a mathematical shortcut to generate successful hashes, you could take over Bitcoin mining.) The Ch "choose" box chooses bits from F or G, based on the value of input E. The Σ "sum" boxes rotate the bits of A (or E) to form three rotated versions, and then sums them together modulo 2. The Ma "majority" box looks at the bits in each position of A, B, and C, and selects 0 or 1, whichever value is in the majority. The red boxes perform 32-bit addition, generating new values for A and E. The input W_t is based on the input data, slightly processed. (This is where the input block gets fed into the algorithm.) The input K_t is a constant defined for each round.

As can be seen from the diagram above, only A and E are changed in a round. The other values pass through unchanged, with the old A value becoming the new B value, the old B value becoming the new C value and so forth. Although each round of SHA-256 doesn't change the data much, after 64 rounds the input data will be completely scrambled, generating the unpredictable hash output.

The IBM 1401

I decided to implement this algorithm on the IBM 1401 mainframe. This computer was announced in 1959, and went on to become the best-selling computer of the mid-1960s, with more than 10,000 systems in use. The 1401 wasn't a very powerful computer even for 1960, but since it leased for the low price of $2500 a month, it made computing possible for mid-sized businesses that previously couldn't have afforded a computer.

The IBM 1401 didn't use silicon chips. In fact it didn't even use silicon. Its transistors were built out of a semiconductor called germanium, which was used before silicon took over. The transistors and other components were mounted on boards the size of playing cards called SMS cards. The computer used thousands of these cards, which were installed in racks called "gates". The IBM 1401 had a couple dozen of these gates, which folded out of the computer for maintenance. Below, one of the gates is opened up showing the circuit boards and cabling.

This shows a rack (called a "gate") folded out of the IBM 1401 mainframe. The photo shows the SMS cards used to implement the circuits. This specific rack controls the tape drives.

Internally, the computer was very different from modern computers. It didn't use 8-bit bytes, but 6-bit characters based on binary coded decimal (BCD). Since it was a business machine, the computer used decimal arithmetic instead of binary arithmetic and each character of storage held a digit, 0 through 9. The computer came with 4000 characters of storage in magnetic core memory; a dishwasher-sized memory expansion box provided 12,000 more characters of storage. The computer was designed to use punched cards as input, with a card reader that read the program and data. Output was printed on a fast line printer or could be punched on more cards.

The Computer History Museum in Mountain View has two working IBM 1401 mainframes. I used one of them to run the SHA-256 hash code. For more information on the IBM 1401, see my article Fractals on the IBM 1401.

Implementing SHA-256 on the IBM 1401

The IBM 1401 is almost the worst machine you could pick to implement the SHA-256 hash algorithm. The algorithm is designed to be implemented efficiently on machines that can do bit operations on 32-bit words. Unfortunately, the IBM 1401 doesn't have 32-bit words or even bytes. It uses 6-bit characters and doesn't provide bit operations. It doesn't even handle binary arithmetic, using decimal arithmetic instead. Thus, implementing the algorithm on the 1401 is slow and inconvenient.

I ended up using one character per bit. A 32-bit value is stored as 32 characters, either "0" or "1". My code has to perform the bit operations and additions character-by-character, basically checking each character and deciding what to do with it. As you might expect, the resulting code is very slow.

The assembly code I wrote is below. The comments should give you a rough idea of how the code works. Near the end of the code, you can see the table of constants required by the SHA-256 algorithm, specified in hex. Since the 1401 doesn't support hex, I had to write my own routines to convert between hex and binary. I won't try to explain IBM 1401 assembly code here, except to point out that it is very different from modern computers. It doesn't even have subroutine calls and returns. Operations happen on memory, as there aren't any general-purpose registers.

               job  bitcoin
     * SHA-256 hash
     * Ken Shirriff  //righto.com
               ctl  6641

               org  087
     X1        dcw  @000@
               org  092
     X2        dcw  @000@
               org  097
     X3        dcw  @000@
     
               org  333
     start     cs   299
               r
               sw   001
               lca  064, input0
               mcw  064, 264
               w
     * Initialize word marks on storage
               mcw  +s0, x3

     wmloop    sw   0&x3  
               ma   @032@, x3
               c    +h7+32, x3
               bu   wmloop
     
               mcw  +input-127, x3      * Put input into warr[0] to warr[15]
               mcw  +warr, x1
               mcw  @128@, tobinc
               b    tobin
     
     * Compute message schedule array w[0..63]
  
               mcw  @16@, i
     * i is word index 16-63   
     * x1 is start of warr[i-16], i.e. bit 0 (bit 0 on left, bit 31 on right)   
               mcw  +warr, x1
     wloop     c    @64@, i
               be   wloopd
     
     * Compute s0
               mcw  +s0, x2
               za   +0, 31&x2               * Zero s0
     * Add w[i-15] rightrotate 7
               sw   7&x2               * Wordmark at bit 7 (from left) of s0
               a    56&x1, 31&x2       * Right shifted: 32+31-7 = bit 24 of w[i-15], 31 = end of s0
               a    63&x1, 6&x2        * Wrapped: 32+31 = end of w[i-15], 7-1 = bit 6 of s0   
               cw   7&x2               * Clear wordmark
     * Add w[i-15] rightrotate 18
               sw   18&x2              * Wordmark at bit 18 (from left) of s0
               a    45&x1, 31&x2       * Right shifted: 32+31-18 = bit 13 of w[i-15], 31 = end of s0
               a    63&x1, 17&x2       * Wrapped: 32+31 = end of w[i-15], 18-1 = bit 17 of s0   
               cw   18&x2              * Clear wordmark
     * Add w[i-15] rightshift 3
               sw   3&x2               * Wordmark at bit 3 (from left) of s0
               a    60&x1, 31&x2       * Right shifted: 32+31-3 = bit 28 of w[i-15], 31 = end of s0
               cw   3&x2               * Clear wordmark
     * Convert sum to xor
               mcw  x1, x1tmp
               mcw  +s0+31, x1         * x1 = right end of s0
               mcw  @032@, x2          * Process 32 bits
               b    xor
               sw   s0                 * Restore wordmark cleared by xor
     
               mcw  x1tmp, x1
     
     * Compute s1         
               mcw  +s1, x2
               za   +0, 31&x2               * Zero s1
     * Add w[i-2] rightrotate 17
               sw   17&x2              * Wordmark at bit 17 (from left) of s1
               a    462&x1, 31&x2      * Right shifted: 14*32+31-17 = bit 14 of w[i-2], 31 = end of s1
               a    479&x1, 16&x2      * Wrapped: 14*32+31 = end of w[i-2], 17-1 = bit 16 of s1   
               cw   17&x2              * Clear wordmark
     * Add w[i-2] rightrotate 19
               sw   19&x2              * Wordmark at bit 19 (from left) of s1
               a    460&x1, 31&x2      * Right shifted: 14*32+31-19 = bit 12 of w[i-2], 31 = end of s1
               a    479&x1, 18&x2      * Wrapped: 14*32+31 = end of w[i-2], 19-1 = bit 18 of s1  
               cw   19&x2              * Clear wordmark
     * Add w[i-2] rightshift 10
               sw   10&x2              * Wordmark at bit 10 (from left) of s1
               a    469&x1, 31&x2      * Right shifted: 14*32+31-10 = bit 21 of w[i-2], 31 = end of s1
               cw   10&x2              * Clear wordmark
     * Convert sum to xor
               mcw  +s1+31, x1         * x1 = right end of s1
               mcw  @032@, x2          * Process 32 bits
               b    xor
               sw   s1                 * Restore wordmark cleared by xor
     
     * Compute w[i] := w[i-16] + s0 + w[i-7] + s1
               mcw  x1tmp, x1
               a    s1+31, s0+31       * Add s1 to s0
               a    31&x1, s0+31       * Add w[i-16] to s0
               a    319&x1, s0+31      * Add 9*32+31 = w[i-7] to s0
     * Convert bit sum to 32-bit sum
               mcw  +s0+31, x1         * x1 = right end of s0
               mcw  @032@, x2          * Process 32 bits
               b    sum
               sw   s0                 * Restore wordmark cleared by sum
     

     
               mcw  x1tmp, x1
               mcw  s0+31, 543&x1      * Move s0 to w[i]
       
              
               ma   @032@, x1
               a    +1, i
               mz   @0@, i
               b    wloop
     
     x1tmp     dcw  #5
     

     * Initialize: Copy hex h0init-h7init into binary h0-h7
     wloopd    mcw  +h0init-7, x3
               mcw  +h0, x1
               mcw  @064@, tobinc       * 8*8 hex digits
               b    tobin
     
     
     * Initialize a-h from h0-h7
               mcw  @000@, x1
     ilp       mcw  h0+31&x1, a+31&x1
               ma   @032@, x1
               c    x1, @256@
               bu   ilp
     
               mcw  @000@, bitidx      * bitidx = i*32 = bit index
               mcw  @000@, kidx        * kidx = i*8 = key index
                

     * Compute s1 from e        
     mainlp    mcw  +e, x1
               mcw  +s1, x2
               za   +0, 31&x2               * Zero s1
     * Add e rightrotate 6
               sw   6&x2               * Wordmark at bit 6 (from left) of s1
               a    25&x1, 31&x2       * Right shifted: 31-6 = bit 25 of e, 31 = end of s1
               a    31&x1, 5&x2        * Wrapped: 31 = end of e, 6-1 = bit 5 of s1   
               cw   6&x2               * Clear wordmark
     * Add e rightrotate 11
               sw   11&x2              * Wordmark at bit 11 (from left) of s1
               a    20&x1, 31&x2       * Right shifted: 31-11 = bit 20 of e, 31 = end of s1
               a    31&x1, 10&x2       * Wrapped: 31 = end of e, 11-1 = bit 10 of s1   
               cw   11&x2              * Clear wordmark
     * Add e rightrotate 25
               sw   25&x2              * Wordmark at bit 25 (from left) of s1
               a    6&x1, 31&x2        * Right shifted: 31-25 = bit 6 of e, 31 = end of s1
               a    31&x1, 24&x2       * Wrapped: 31 = end of e, 25-1 = bit 24 of s1   
               cw   25&x2              * Clear wordmark
     * Convert sum to xor
               mcw  +s1+31, x1         * x1 = right end of s1
               mcw  @032@, x2          * Process 32 bits
               b    xor
               sw   s1                 * Restore wordmark cleared by xor

     * Compute ch: choose function
               mcw  @000@, x1          * x1 is index from 0 to 31
     chl       c    e&x1, @0@
               be   chzero
               mn   f&x1, ch&x1        * for 1, select f bit
               b    chincr
     chzero    mn   g&x1, ch&x1        * for 0, select g bit
     chincr    a    +1, x1
               mz   @0@, x1
               c    @032@, x1
               bu   chl

     * Compute temp1: k[i] + h + S1 + ch + w[i]
               cs   299
               mcw  +k-7, x3            * Convert k[i] to binary in temp1
               ma   kidx, x3
               mcw  +temp1, x1
               mcw  @008@, tobinc       * 8 hex digits
               b    tobin
               mcw  @237@, x3
               mcw  +temp1, x1
               mcw  @008@, tobinc
               b    tohex
               a    h+31, temp1+31     * +h
               a    s1+31, temp1+31    * +s1
               a    ch+31, temp1+31    * +ch
               mcw  bitidx, x1
               a    warr+31&x1, temp1+31         * + w[i]
     * Convert bit sum to 32-bit sum
               mcw  +temp1+31, x1      * x1 = right end of temp1
               b    sum
  

     * Compute s0 from a
               mcw  +a, x1
               mcw  +s0, x2
               za   +0, 31&x2               * Zero s0
     * Add a rightrotate 2
               sw   2&x2               * Wordmark at bit 2 (from left) of s0
               a    29&x1, 31&x2       * Right shifted: 31-2 = bit 29 of a, 31 = end of s0
               a    31&x1, 1&x2        * Wrapped: 31 = end of a, 2-1 = bit 1 of s0   
               cw   2&x2               * Clear wordmark
     * Add a rightrotate 13
               sw   13&x2              * Wordmark at bit 13 (from left) of s0
               a    18&x1, 31&x2       * Right shifted: 31-13 = bit 18 of a, 31 = end of s0
               a    31&x1, 12&x2       * Wrapped: 31 = end of a, 13-1 = bit 12 of s0   
               cw   13&x2              * Clear wordmark
     * Add a rightrotate 22
               sw   22&x2              * Wordmark at bit 22 (from left) of s0
               a    9&x1, 31&x2        * Right shifted: 31-22 = bit 9 of a, 31 = end of s0
               a    31&x1, 21&x2       * Wrapped: 31 = end of a, 22-1 = bit 21 of s0   
               cw   22&x2              * Clear wordmark
     * Convert sum to xor
               mcw  +s0+31, x1         * x1 = right end of s0
               mcw  @032@, x2          * Process 32 bits
               b    xor
               sw   s0                 * Restore wordmark cleared by xor

     * Compute maj(a, b, c): majority function
               za   +0, maj+31
               a    a+31, maj+31
               a    b+31, maj+31
               a    c+31, maj+31
               mz   @0@, maj+31
               mcw  @000@, x1          * x1 is index from 0 to 31
     mjl       c    maj&x1, @2@
               bh   mjzero
               mn   @1@, maj&x1       * majority of the 3 bits is 1
               b    mjincr
     mjzero    mn   @0@, maj&x1       * majority of the 3 bits is 0
     mjincr    a    +1, x1
               mz   @0@, x1
               c    @032@, x1
               bu   mjl

     * Compute temp2: S0 + maj
               za   +0, temp2+31
               a    s0+31, temp2+31
               a    maj+31, temp2+31
     * Convert bit sum to 32-bit sum
               mcw  +temp2+31, x1      * x1 = right end of temp1
               b    sum
     
               mcw  g+31, h+31         * h := g
               mcw  f+31, g+31         * g := f
               mcw  e+31, f+31         * f := e
               za   +0, e+31           * e := d + temp1
               a    d+31, e+31
               a    temp1+31, e+31
               mcw  +e+31, x1          * Convert sum to 32-bit sum
               b    sum
               mcw  c+31, d+31         * d := c
               mcw  b+31, c+31         * c := b
               mcw  a+31, b+31         * b := a
               za   +0, a+31           * a := temp1 + temp2
               a    temp1+31, a+31
               a    temp2+31, a+31
               mcw  +a+31, x1          * Convert sum to 32-bit sum
               b    sum

               a    @8@, kidx          * Increment kidx by 8 chars
               mz   @0@, kidx
               ma   @032@, bitidx      * Increment bitidx by 32 bits
               c    @!48@, bitidx      * Compare to 2048
               bu   mainlp

     * Add a-h to h0-h7
               cs   299
               mcw  @00000@, x1tmp  
     add1      mcw  x1tmp, x1
               a    a+31&x1, h0+31&x1
               ma   +h0+31, x1          * Convert sum to 32-bit sum
               b    sum     
               ma   @032@, x1tmp
               c    @00256@, x1tmp
               bu   add1
               mcw  @201@, x3
               mcw  +h0, x1
               mcw  @064@, tobinc
               b    tohex
               w
               mcw  280, 180
               p
               p

     finis     h
               b    finis

      
     * Converts sum of bits to xor
     * X1 is right end of word
     * X2 is bit count    
     * Note: clears word marks
     xor       sbr  xorx&3
     xorl      c    @000@, x2
               be   xorx
     xorfix    mz   @0@, 0&x1          * Clear zone
               c    0&x1, @2@
               bh   xorok
               sw   0&x1               * Subtract 2 and loop
               s    +2, 0&x1
               cw   0&x1
               b    xorfix
     xorok     ma   @I9I@, x1         * x1 -= 1
               s    +1, x2             * x2 -= 1
               mz   @0@, x2
               b    xorl               * loop
     
     xorx      b    @000@
     
     * Converts sum of bits to sum (i.e. propagate carries if digit > 1)
     * X1 is right end of word
     * Ends at word mark
     sum       sbr  sumx&3
     suml      mz   @0@, 0&x1          * Clear zone
               c    0&x1, @2@          * If digit is <2, then ok
               bh   sumok
               s    +2, 0&x1           * Subtract 2 from digit
               bwz  suml, 0&x1, 1      * Skip carry if at wordmark
               a    @1@, 15999&x1      * Add 1 to previous position
               b    suml               * Loop
     sumok     bwz  sumx,0&x1,1        * Quit if at wordmark
               ma   @I9I@, x1          * x1 -= 1
               b    suml               * loop
     sumx      b    @000@              * return
     
     * Converts binary to string of hex digits
     * X1 points to start (left) of binary
     * X3 points to start (left) of hex buffer
     * X1, X2, X3 destroyed
     * tobinc holds count (# of hex digits)
     tohex     sbr  tohexx&3
     tohexl    c    @000@, tobinc      * check counter
               be   tohexx
               s    @1@, tobinc        * decrement counter
               mz   @0@, tobinc
               b    tohex4
               mcw  hexchr, 0&x3
               ma   @004@, X1
               ma   @001@, X3
               b    tohexl             * loop
     tohexx    b    @000@ 
     

     
     * X1 points to 4 bits
     * Convert to hex char and write into hexchr
     * X2 destroyed

     tohex4    sbr  tohx4x&3
               mcw  @000@, x2
               c    3&X1, @1@
               bu   tohx1
               a    +1, x2
     tohx1     c    2&X1, @1@
               bu   tohx2
               a    +2, x2
     tohx2     c    1&x1, @1@
               bu   tohx4
               a    +4, x2
     tohx4     c    0&x1, @1@
               bu   tohx8
               a    +8, x2
     tohx8     mz   @0@, x2
               mcw  hextab-15&x2, hexchr
     tohx4x    b    @000@
     
     * Converts string of hex digits to binary
     * X3 points to start (left) of hex digits
     * X1 points to start (left) of binary digits
     * tobinc holds count (# of hex digits)
     * X1, X3 destroyed
     tobin     sbr  tobinx&3
     tobinl    c    @000@, tobinc      * check counter
               be   tobinx
               s    @1@, tobinc        * decrement counter
               mz   @0@, tobinc
               mcw  0&X3, hexchr
               b    tobin4             * convert 1 char
               ma   @004@, X1
               ma   @001@, X3
               b    tobinl             * loop
     tobinx    b    @000@
               
     
     tobinc    dcw  @000@
     * Convert hex digit to binary
     * Digit in hexchr (destroyed)
     * Bits written to x1, ..., x1+3
     tobin4    sbr  tobn4x&3
               mcw  @0000@, 3+x1   * Start with zero bits
               bwz  norm,hexchr,2  * Branch if no zone
              
               mcw  @1@, 0&X1
               a    @1@, hexchr    * Convert letter to value: A (1) -> 2, F (6) -> 7
               mz   @0@, hexchr
               b    tob4
     norm      c    @8@, hexchr
               bl   tob4
               mcw  @1@, 0&X1
               s    @8@, hexchr
               mz   @0@, hexchr
     tob4      c    @4@, hexchr
               bl   tob2
               mcw  @1@, 1&X1
               s    @4@, hexchr
               mz   @0@, hexchr
     tob2      c    @2@, hexchr
               bl   tob1
               mcw  @1@, 2&X1
               s    @2@, hexchr
               mz   @0@, hexchr
     tob1      c    @1@, hexchr
               bl   tobn4x
               mcw  @1@, 3&X1
     tobn4x    b    @000@          


     
     * Message schedule array is 64 entries of 32 bits = 2048 bits.
               org  3000
     warr      equ  3000
     
     s0        equ  warr+2047                *32 bits
     s1        equ  s0+32 
     ch        equ  s1+32              *32 bits

     temp1     equ  ch+32               *32 bits
     
     temp2     equ  temp1+32                *32 bits
     
     maj       equ  temp2+32                *32 bits
     
     a         equ  maj+32
     b         equ  a+32
     c         equ  b+32
     d         equ  c+32
     e         equ  d+32
     f         equ  e+32
     g         equ  f+32
     h         equ  g+32
     h0        equ  h+32
     h1        equ  h0+32
     h2        equ  h1+32
     h3        equ  h2+32
     h4        equ  h3+32
     h5        equ  h4+32
     h6        equ  h5+32
     h7        equ  h6+32
               org  h7+32
 
     hexchr    dcw  @0@
     hextab    dcw  @0123456789abcdef@    
     i         dcw  @00@               * Loop counter for w computation
     bitidx    dcw  #3
     kidx      dcw  #3         
     
     * 64 round constants for SHA-256
     k         dcw  @428a2f98@
               dcw  @71374491@
               dcw  @b5c0fbcf@
               dcw  @e9b5dba5@
               dcw  @3956c25b@
               dcw  @59f111f1@
               dcw  @923f82a4@
               dcw  @ab1c5ed5@
               dcw  @d807aa98@
               dcw  @12835b01@
               dcw  @243185be@
               dcw  @550c7dc3@
               dcw  @72be5d74@
               dcw  @80deb1fe@
               dcw  @9bdc06a7@
               dcw  @c19bf174@
               dcw  @e49b69c1@
               dcw  @efbe4786@
               dcw  @0fc19dc6@
               dcw  @240ca1cc@
               dcw  @2de92c6f@
               dcw  @4a7484aa@
               dcw  @5cb0a9dc@
               dcw  @76f988da@
               dcw  @983e5152@
               dcw  @a831c66d@
               dcw  @b00327c8@
               dcw  @bf597fc7@
               dcw  @c6e00bf3@
               dcw  @d5a79147@
               dcw  @06ca6351@
               dcw  @14292967@
               dcw  @27b70a85@
               dcw  @2e1b2138@
               dcw  @4d2c6dfc@
               dcw  @53380d13@
               dcw  @650a7354@
               dcw  @766a0abb@
               dcw  @81c2c92e@
               dcw  @92722c85@
               dcw  @a2bfe8a1@
               dcw  @a81a664b@
               dcw  @c24b8b70@
               dcw  @c76c51a3@
               dcw  @d192e819@
               dcw  @d6990624@
               dcw  @f40e3585@
               dcw  @106aa070@
               dcw  @19a4c116@
               dcw  @1e376c08@
               dcw  @2748774c@
               dcw  @34b0bcb5@
               dcw  @391c0cb3@
               dcw  @4ed8aa4a@
               dcw  @5b9cca4f@
               dcw  @682e6ff3@
               dcw  @748f82ee@
               dcw  @78a5636f@
               dcw  @84c87814@
               dcw  @8cc70208@
               dcw  @90befffa@
               dcw  @a4506ceb@
               dcw  @bef9a3f7@
               dcw  @c67178f2@
     * 8 initial hash values for SHA-256
     h0init    dcw  @6a09e667@
     h1init    dcw  @bb67ae85@
     h2init    dcw  @3c6ef372@
     h3init    dcw  @a54ff53a@
     h4init    dcw  @510e527f@
     h5init    dcw  @9b05688c@
     h6init    dcw  @1f83d9ab@
     h7init    dcw  @5be0cd19@


     input0    equ  h7init+64
               org  h7init+65

               dc   @80000000000000000000000000000000@
     input     dc   @00000000000000000000000000000100@      * 512 bits with the mostly-zero padding

               end  start

I punched the executable onto a deck of about 85 cards, which you can see at the beginning of the article. I also punched a card with the input to the hash algorithm. To run the program, I loaded the card deck into the card reader and hit the "Load" button. The cards flew through the reader at 800 cards per minute, so it took just a few seconds to load the program. The computer's console (below) flashed frantically for 40 seconds while the program ran. Finally, the printer printed out the resulting hash (as you can see at the top of the article) and the results were punched onto a new card. Since Bitcoin mining used double SHA-256 hashing, hashing for mining would take twice as long (80 seconds).

The console of the IBM 1401 shows a lot of activity while computing a SHA-256 hash.

Performance comparison

The IBM 1401 can compute a double SHA-256 hash in 80 seconds. It requires about 3000 Watts of power, roughly the same as an oven or clothes dryer. A basic IBM 1401 system sold for $125,600, which is about a million dollars in 2015 dollars. On the other hand, today you can spend $50 and get a USB stick miner with a custom ASIC integrated circuit. This USB miner performs 3.6 billion hashes per second and uses about 4 watts. The enormous difference in performance is due to several factors: the huge increase in computer speed in the last 50 years demonstrated by Moore's law, the performance lost by using a decimal business computer for a binary-based hash, and the giant speed gain from custom Bitcoin mining hardware.

To summarize, to mine a block at current difficulty, the IBM 1401 would take about 5x10^14 years (about 40,000 times the current age of the universe). The electricity would cost about 10^18 dollars. And you'd get 25 bitcoins worth about $6000. Obviously, mining Bitcoin on an IBM 1401 mainframe is not a profitable venture. The photos below compare the computer circuits of the 1960s with the circuits of today, making it clear how much technology has advanced.

On the left, SMS cards inside the IBM 1401. Each card has a handful of components and implements a circuit such as a gate. The computer contains more than a thousand of these cards. On the right, the Bitfury ASIC chip for mining Bitcoins does 2-3 Ghash/second. Image from zeptobars (CC BY 3.0 license)

Networking

You might think that Bitcoin would be impossible with 1960s technology due to the lack of networking. Would one need to mail punch cards with the blockchain to the other computers? While you might think of networked computers as a modern thing, IBM supported what they call teleprocessing as early as 1941. In the 1960s, the IBM 1401 could be hooked up to the IBM 1009 Data Transmission Unit, a modem the size of a dishwasher that could transfer up to 300 characters per second over a phone line to another computer. So it would be possible to build a Bitcoin network with 1960s-era technology. Unfortunately I didn't have teleprocessing hardware available to test this out.

IBM 1009 Data Transmission Unit. This dishwasher-sized modem was introduced in 1960 and can transmit up to 300 characters per second over phone lines. Photo from Introduction to IBM Data Processing Systems.

Conclusion

Implementing SHA-256 in assembly language for an obsolete mainframe was a challenging but interesting project. Performance was worse than I expected (even compared to my 12 minute Mandelbrot). The decimal arithmetic of a business computer is a very poor match for a binary-optimized algorithm like SHA-256. But even a computer that predates integrated circuits can implement the Bitcoin mining algorithm. And, if I ever find myself back in 1960 due to some strange time warp, now I know how to set up a Bitcoin network.

The Computer History Museum in Mountain View runs demonstrations of the IBM 1401 on Wednesdays and Saturdays so if you're in the area you should definitely check it out (schedule). Tell the guys running the demo that you heard about it from me and maybe they'll run my Pi program for you. Thanks to the Computer History Museum and the members of the 1401 restoration team, Robert Garner, Ed Thelen, Van Snyder, and especially Stan Paddock. The 1401 team's website (ibm-1401.info) has a ton of interesting information about the 1401 and its restoration.

Disclaimers

I would like to be clear that I am not actually mining real Bitcoin on the IBM 1401—the Computer History Museum would probably disapprove of that. As I showed above, there's no way you could make money off mining on the IBM 1401. I did, however, really implement and run the SHA-256 algorithm on the IBM 1401, showing that mining is possible in theory. And if you're wondering how I found a successful hash, I simply used a block that had already been mined: block #286819.