While programmers today take multiplication for granted, most microprocessors in the 1970s could only add and subtract — multiplication required a slow and tedious loop implemented in assembly code.1 One of the nice features of the Intel 8086 processor (1978) was that it provided machine instructions for multiplication,2 able to multiply 8-bit or 16-bit numbers with a single instruction. Internally, the 8086 still performed a loop, but the loop was implemented in microcode: faster and transparent to the programmer. Even so, multiplication was a slow operation, about 24 to 30 times slower than addition.
In this blog post, I explain the multiplication process inside the 8086, analyze the microcode that it used, and discuss the hardware circuitry that helped it out.3 My analysis is based on reverse-engineering the 8086 from die photos. The die photo below shows the chip under a microscope. I've labeled the key functional blocks; the ones that are important to this post are darker. At the left, the ALU (Arithmetic/Logic Unit) performs the arithmetic operations at the heart of multiplication: addition and shifts. Multiplication also uses a few other hardware features: the X register, the F1 flag, and a loop counter. The microcode ROM at the lower right controls the process.
Microcode
The multiplication routines in the 8086 are implemented in microcode. Most people think of machine instructions as the basic steps that a computer performs. However, many processors (including the 8086) have another layer of software underneath: microcode. With microcode, instead of building the control circuitry from complex logic gates, the control logic is largely replaced with code. To execute a machine instruction, the computer internally executes several simpler micro-instructions, specified by the microcode. This is especially useful for a machine instruction such as multiplication, which requires many steps in a loop.
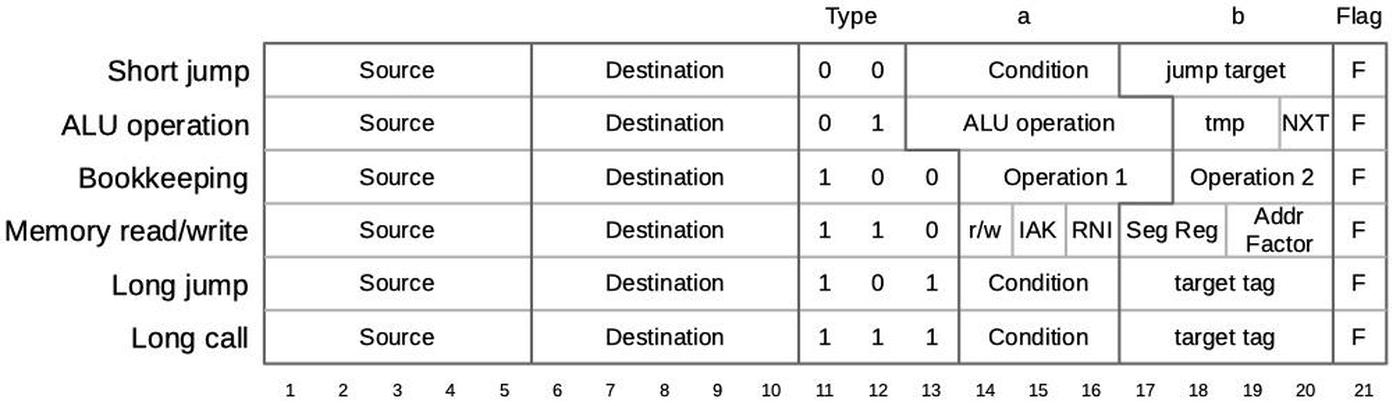
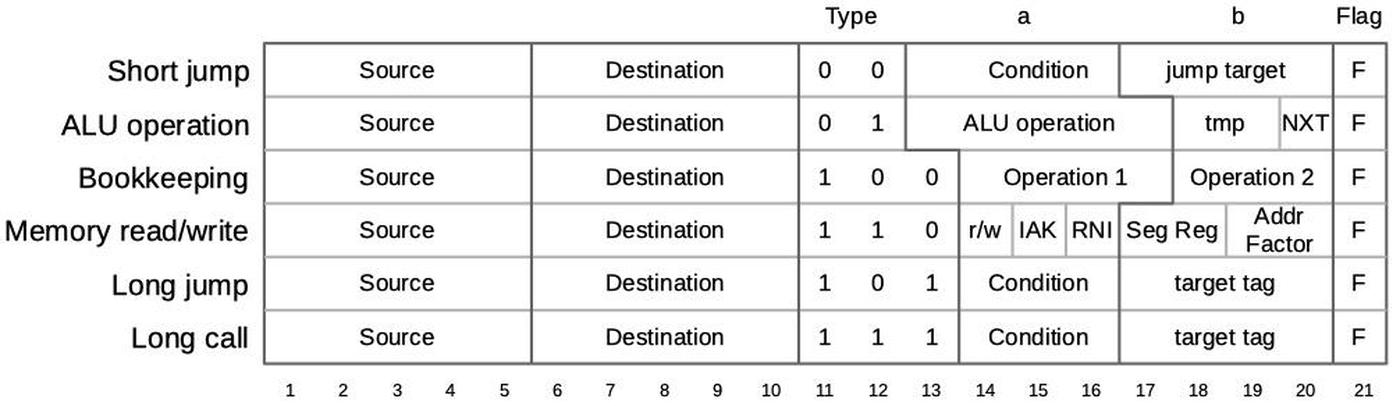
A micro-instruction in the 8086 is encoded into 21 bits as shown below. Every micro-instruction has a move from a source register to a destination register, each specified with 5 bits. The meaning of the remaining bits depends on the type field and can be anything from an ALU operation to a memory read or write to a change of microcode control flow. Thus, an 8086 micro-instruction typically does two things in parallel: the move and the action. For more about 8086 microcode, see my microcode blog post.
The behavior of an ALU micro-operation is important for multiplication.
The ALU has three temporary registers that are invisible to the programmer: tmpA, tmpB, and tmpC.
An ALU operation takes its first argument from any temporary register, while the second argument always comes from tmpB.
An ALU operation requires two micro-instructions.
The first micro-instruction specifies the ALU operation and source register, configuring the ALU. For instance, ADD tmpA to add tmpA to the default tmpB.
In the next micro-instruction (or a later one), the ALU result can be accessed through the Σ register and moved to another register.
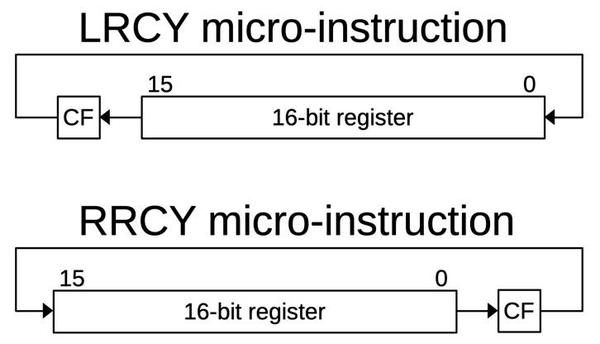
Before I get into the microcode routines, I should explain two ALU operations that play a central role in multiplication: LRCY and RRCY, Left Rotate through Carry and Right Rotate through Carry.
(These correspond to the RCL and RCR machine instructions, which rotate through carry left or right.)
These operations shift the bits in a 16-bit word, similar to the << and >> bit-shift operations in high-level languages, but with an additional feature.
Instead of discarding the bit on the end, that bit is moved into the carry flag (CF). Meanwhile, the bit formerly in the carry flag moves into the word.
You can think of this as rotating the bits while treating the carry flag as a 17th bit of the word.
These shifts perform an important part of the multiplication process since shifting can be viewed as multiplying by two.
LRCY also provides a convenient way to move the most-significant bit to the carry flag, where it can be tested for a conditional jump.
(This is important because the top bit is used as the sign bit.)
Similarly, RRCY provides access to the least significant bit, very important for the multiplication process.
Another important property is that performing RRCY on an upper word and then RRCY on a lower word will perform a 32-bit shift, since
the low bit of the upper word will be moved into the high bit of the lower word via the carry bit.
Binary multiplication
The shift-and-add method of multiplication (below) is similar to grade-school long multiplication, except it uses binary instead of decimal. In each row, the multiplicand is multiplied by one digit of the multiplier. (The multiplicand is the value that gets repeatedly added, and the multiplier controls how many times it gets added.) Successive rows are shifted left one digit. At the bottom, the rows are added together to yield the product. The example below shows how 6×5 is calculated in binary using long multiplication.
×0101
0110
0000
0110
0000
00011110
Binary long multiplication is much simpler than decimal multiplication: at each step, you're multiplying by 0 or 1. Thus, each row is either zero or the multiplicand appropriately shifted (0110 in this case). (Unlike decimal long multiplication, you don't need to know the multiplication table.) This simplifies the hardware implementation, since each step either adds the multiplicand or doesn't. In other words, each step tests a bit of the multiplier, starting with the low bit, to determine if an add should take place or not. This bit can be obtained by shifting the multiplier one bit to the right each step.
Although the diagram above shows the sum at the end, a real implementation performs the addition at each step of the loop, keeping a running total. Moreover, in the 8086, instead of shifting the multiplicand to the left during each step, the sum shifts to the right. (The result is the same but it makes the implementation easier.) Thus, multiplying 6×5 goes through the steps below.
×0110
00000
001010
0011110
00011110
Why would you shift the result to the right?
There's a clever reason for this.
Suppose you're multiplying two 16-bit numbers, which yields a 32-bit result. That requires four 16-bit words of storage if you use the
straightforward approach.
But if you look more closely, the first sum fits into 16 bits, and then you need one more bit at each step. Meanwhile, you're "using up"
one bit of the multiplier at each step.
So if you squeeze the sum and the multiplier together, you can fit them into two words.
Shifting right accomplishes this, as the diagram below illustrates for 0xffff×0xf00f. The sum (blue) starts in a 16-bit register called tmpA
while the multiplier (green) is stored in the 16-bit tmpB register.
In each step, they are both shifted right, so the sum gains one bit and the multiplier loses one bit. By the end, the sum takes up all 32 bits,
split across both registers.
| sum (tmpA) | multiplier (tmpC) | ||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 |
The multiplication microcode
The 8086 has four multiply instructions to handle signed and unsigned multiplication of byte and word operands.
These machine instructions are implemented in microcode.
I'll start by describing the unsigned word multiplication, which multiplies two 16-bit values and produces a 32-bit result.
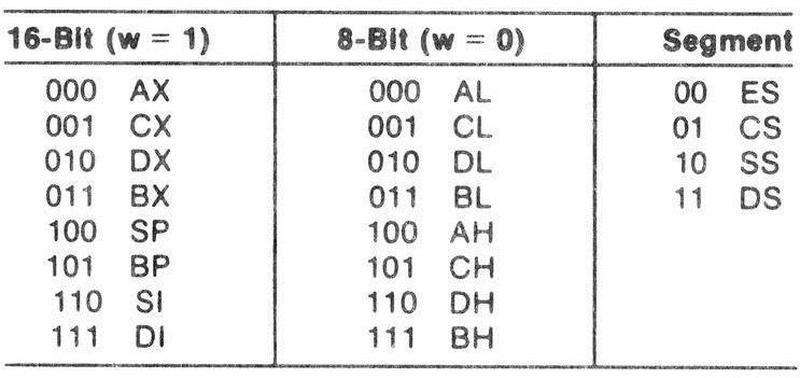
The source word is provided by either a register or memory. It is multiplied by AX, the accumulator register.
The 32-bit result is returned in the DX and AX registers.
The microcode below is the main routine for word multiplication, both signed and unsigned. Each micro-instruction specifies a register move on the left, and an action on the right. The moves transfer words between the visible registers and the ALU's temporary registers, while the actions are mostly subroutine calls to other micro-routines.
move action AX → tmpC LRCY tmpC iMUL rmw: M → tmpB CALL X0 PREIMUL called for signed multiplication CALL CORX the core routine CALL F1 NEGATE called for negative result CALL X0 IMULCOF called for signed multiplication tmpC → AX JMPS X0 7 CALL MULCOF called for unsigned multiplication tmpA → DX RNI
The microcode starts by moving one argument AX into the ALU's temporary C register and setting up the ALU to perform a Left Rotate through Carry on this register, in order to access the sign bit.
Next, it moves the second argument M into the temporary B register; M references the register or memory specified in the second byte
of the instruction, the "ModR/M" byte.
For a signed multiply instruction, the PREIMUL micro-subroutine is called, but I'll skip that for now.
(The X0 condition tests bit 3 of the instruction, which in this case distinguishes MUL from IMUL.)
Next, the CORX subroutine is called, which is the heart of the multiplication.4
If the result needs to be negated (indicated by the F1 condition), the NEGATE micro-subroutine is called.
For signed multiplication, IMULCOF is then called to set the carry and overflow flags, while MULCOF is called for unsigned multiplication.
Meanwhile, the result bytes are moved from the temporary C and temporary registers to the AX and DX registers.
Finally, RNI runs the next machine instruction, ending the microcode routine.
CORX
The heart of the multiplication code is the CORX routine, which performs the multiplication loop, computing the product through shifts and adds.
The first two lines set up the loop, initializing the sum (tmpA) to 0.
The number of loops is controlled by a special-purpose loop counter.
The MAXC micro-instruction initializes the counter to 7 or 15, for a byte or word multiply respectively.
The first shift of tmpC is performed, putting the low bit into the carry flag.
The loop body performs the shift-and-add step.
It tests the carry flag, the low bit of the multiplicand. It skips over the ADD if there is no carry (NCY).
Otherwise, tmpB is added to tmpA. (As tmpA gets shifted to the right, tmpB gets added to higher and higher positions in the result.)
The tmpA and tmpC registers are rotated right. This also puts the next bit of the multiplicand into the carry flag for the next cycle.
The microcode jumps to the top of the loop if the counter is not zero (NCZ). Otherwise, the subroutine returns with the result in tmpA and tmpC.
ZERO → tmpA RRCY tmpC CORX: initialize right rotate Σ → tmpC MAXC get rotate result, initialize counter to max value JMPS NCY 8 5: top of loop ADD tmpA conditionally add Σ → tmpA F sum to tmpA, update flags to get carry RRCY tmpA 8: 32-bit shift of tmpA/tmpC Σ → tmpA RRCY tmpC Σ → tmpC JMPS NCZ 5 loop to 5 if counter is not 0 RTN
MULCOF
The last subroutine is MULCOF, which configures the carry and overflow flags.
The 8086 uses the rule that if the upper half of the result is nonzero, the carry and overflow flags are set, otherwise they are cleared.
The first two lines pass tmpA (the upper half of the result) through the ALU to set the
zero flag for the conditional jump. As a side-effect, the other status flags will get set but these values are "undefined" in the documentation.6
If the test is nonzero, the carry and overflow flags are set (SCOF), otherwise they are cleared (CCOF).5
The SCOF and CCOF micro-operations were implemented solely for used by multiplication, illustrating how microcode can be designed around
specific needs.
PASS tmpA MULCOF: pass tmpA through to test if zero
Σ → no dest JMPS 12 F update flags
JMPS Z 8 12: jump if zero
SCOF RTN otherwise set carry and overflow
CCOF RTN 8: clear carry and overflow
8-bit multiplication
The 8086 has separate instructions for 8-bit multiplication. The process for 8-bit multiplication is similar to 16-bit multiplication, except the values are half as long and the shift-and-add loop executes 8 times instead of 16. As shown below, the 8-bit sum starts in the low half of the temporary A register and is shifted left into tmpC. Meanwhile, the 8-bit multiplier starts in the low half of tmpC and is shifted out to the right. At the end, the result is split between tmpA and tmpC.
| sum (tmpA) | multiplier (tmpC) | ||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
The 8086 supports many instructions with byte and word versions, using 8-bit or 16-bit arguments.
In most cases, the byte and word instructions use the same microcode, with the ALU and register hardware using bytes or words based on the instruction.
However, the byte- and word-multiply instructions use different registers, requiring microcode changes.
In particular, the multiplier is in AL, the low half of the accumulator.
At the end, the 16-bit result is returned in AX, the full 16-bit accumulator; two micro-instructions assemble the result from tmpC and tmpA into
the two bytes of the accumulator, 'AL' and 'AH' respectively.
Apart from those changes, the microcode is the same as the word multiply microcode discussed earlier.
AL → tmpC LRCY tmpC iMUL rmb:
M → tmpB CALL X0 PREIMUL
CALL CORX
CALL F1 NEGATE
CALL X0 IMULCOF
tmpC → AL JMPS X0 7
CALL MULCOF
tmpA → AH RNI
Signed multiplication
The 8086 (like most computers) represents signed numbers using a format called two's complement.
While a regular byte holds a number from 0 to 255, a signed byte holds a number from -128 to 127.
A negative number is formed by flipping all the bits (known as the one's complement) and then adding 1, yielding the two's complement value.7
For instance, +5 is 0x05 while -5 is 0xfb.
(Note that the top bit of a number is set for a negative number; this is the sign bit.)
The nice thing about two's complement numbers is that the same addition and subtraction operations work on both signed and unsigned values.
Unfortunately, this is not the case for signed multiplication, since signed and unsigned values yield different results due to sign extension.
The 8086 has separate multiplication instructions IMUL (Integer Multiply) to perform signed multiplication.
The 8086 performs signed multiplication by converting the arguments to positive values, performing unsigned multiplication, and then
negating the result if necessary.
As shown above, signed and unsigned multiplication both use the same microcode, but the microcode conditionally calls some subroutines for
signed multiplication.
I will discuss those micro-subroutines below.
PREIMUL
The first subroutine for signed multiplication is PREIMUL, performing preliminary operations for integer multiplication.
It converts the two arguments, stored in tmpC and tmpB, to positive values.
It keeps track of the signs using an internal flag called F1, toggling this flag for a negative argument.
This conveniently handles the rule that two negatives make a positive since complementing the F1 flag twice will clear it.
This microcode, below, illustrates the complexity of microcode and how micro-operations are carefully arranged to get the right values at the right time.
The first micro-instruction performs one ALU operation and sets up a second operation.
The calling code had set up the ALU to perform LRCY tmpC, so that's the result returned by Σ (and discarded).
Performing a left rotate and discarding the result may seem pointless, but the important side-effect is that the top bit
(i.e. the sign bit) ends up in the carry flag.
The microcode does not have a conditional jump based on the sign, but has a conditional jump based on carry, so the point is
to test if tmpC is negative.
The first micro-instruction also sets up negation (NEG tmpC) for the next ALU operation.
Σ → no dest NEG tmpC PREIMUL: set up negation of tmpC JMPS NCY 7 jump if tmpC positive Σ → tmpC CF1 if negative, negate tmpC, flip F1 JMPS 7 jump to shared code LRCY tmpB 7: Σ → no dest NEG tmpB set up negation of tmpB JMPS NCY 11 jump if tmpB positive Σ → tmpB CF1 RTN if negative, negate tmpB, flip F1 RTN 11: return
For the remaining lines,
if the carry is clear (NCY), the next two lines are skipped. Otherwise, the ALU result (Σ) is written to tmpC, making it positive,
and the F1 flag is complemented with CF1. (The second short jump (JMPS) may look unnecessary, but I reordered the code for clarity.)
The second half of the microcode performs a similar test on tmpB. If tmpB is negative, it is negated and F1 is toggled.
NEGATE
The microcode below is called after computing the result, if the result needs to be made negative.
Negation is harder than you might expect because the result is split between the tmpA and tmpC registers.
The two's complement operation (NEG) is applied to the low word, while either 2's complement or one's complement (COM1) is applied to
the upper word, depending on the carry for mathematical reasons.8
The code also toggles F1 and makes tmpB positive; I think this code is only useful for division, which also uses the NEGATE subroutine.
NEG tmpC NEGATE: negate tmpC
Σ → tmpC COM1 tmpA F maybe complement tmpA
JMPS CY 6
NEG tmpA negate tmpA if there's no carry
Σ → tmpA CF1 6: toggle F1 for some reason
LRCY tmpB 7: test sign of tmpB
Σ → no dest NEG tmpB maybe negate tmpB
JMPS NCY 11 skip if tmpB positive
Σ → tmpB CF1 RTN else negate tmpB, toggle F1
RTN 11: return
IMULCOF
The IMULCOF routine is similar to MULCOF, but the calculation is a bit trickier for a signed result.
This routine sets the carry and overflow flags if the upper half of the result is significant, that is, it is not
just the sign extension of the lower half.9
In other words, the top byte is not significant if it duplicates the top bit (the sign bit) of the lower byte.
The trick in the microcode is to add the top bit of the lower byte to the upper byte by putting it in the carry flag
and performing an add with carry (ADC) of 0.
If the result is 0, the upper byte is not significant, handling the positive and negative cases.
(This also holds for words instead of bytes.)
ZERO → tmpB LRCY tmpC IMULCOF: get top bit of tmpC Σ → no dest ADC tmpA add to tmpA and 0 (tmpB) Σ → no dest F update flags JMPS Z 8 12: jump if zero result SCOF RTN otherwise set carry and overflow CCOF RTN 8: clear carry and overflow
The hardware for multiplication
For the most part, the 8086 uses the regular ALU addition and shifts for the multiplication algorithm. Some special hardware features provide assistance.
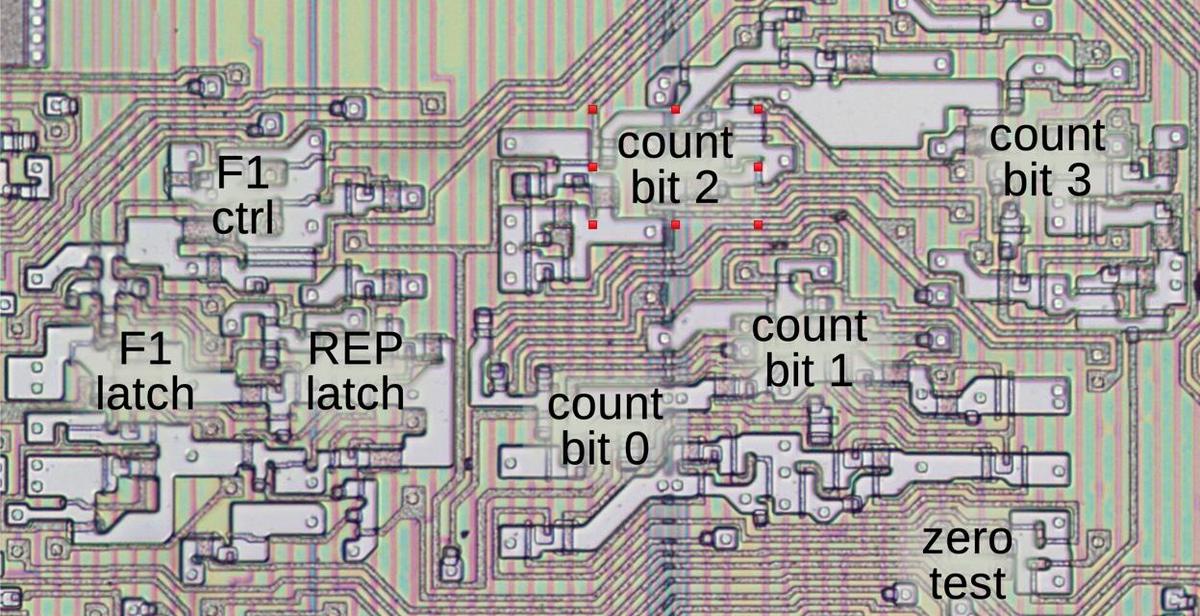
Loop counter
The 8086 has a special 4-bit loop counter for multiplication. This counter starts at 7 for byte multiplication and 15 for word multiplication,
based on the instruction.
This loop counter allows the microcode to decrement the counter, test for the end, and perform a conditional branch in one micro-operation.
The counter is implemented with four flip-flops, along with logic to compute the value after decrementing by one.
The MAXC (Maximum Count) micro-instruction sets the counter to 7 or 15 for byte or word operations respectively.
The NCZ (Not Counter Zero) micro-instruction has two actions. First, it performs a conditional jump if the counter is nonzero.
Second, it decrements the counter.
X register
The multiplication microcode uses an internal register called the X register to distinguish between the MUL and IMUL instructions.
The X register is a 3-bit register that holds the ALU opcode, indicated by bits 5–3 of the instruction.10
Since the instruction is held in the Instruction Register, you might wonder why a separate register is required.
The motivation is that some opcodes specify the type of ALU operation in the second byte of the instruction, the ModR/M byte, bits 5–3.11
Since the ALU operation is sometimes specified in the first byte and sometimes in the second byte, the X register was added to handle
both these cases.
For the most part, the X register indicates which of the eight standard ALU operations is selected (ADD, OR, ADC, SBB, AND, SUB, XOR, CMP).
However, a few instructions use bit 0 of the X register to distinguish between other pairs of instructions.
For instance, it distinguishes between MUL and IMUL, DIV and IDIV, CMPS and SCAS, MOVS and LODS, or AAA and AAS.
While these instruction pairs may appear to have arbitrary opcodes, they have been carefully assigned.
The microcode can test this bit using the X0 condition and perform conditional jumps.
The implementation of the X register is straightforward, consisting of three flip-flops to hold the three bits of the instruction.
The flip-flops are loaded from the prefetch queue bus during First Clock and during Second Clock for appropriate instructions, as the
instruction bytes travel over the bus.
Testing bit 0 of the X register with the X0 condition is supported by the microcode condition evaluation circuitry, so it can be used for conditional jumps in the microcode.
The F1 flag
The multiplication microcode uses an internal flag called F1,12 which has two distinct uses.
The flag keeps track of a REP prefix for use with a string operation.
But the F1 flag is also used by signed multiplication and division to keep track of the sign.
The F1 flag can be toggled by microcode through the CF1 (Complement F1) micro-instruction.
The F1 flag is implemented with a flip-flop, along with a multiplexer to select the value. It is cleared when a new instruction starts,
set by a REP prefix, and toggled by the CF1 micro-instruction.
The diagram below shows how the F1 latch and the loop counter appear on the die. In this image, the metal layer has been removed, showing the silicon and the polysilicon wiring underneath.
Later advances in multiplication
The 8086 was pretty slow at multiplying compared to later Intel processors.13 The 8086 took up to 133 clock cycles to multiply unsigned 16-bit values due to the complicated microcode loops. By 1982, the Intel 286 processor cut this time down to 21 clock cycles. The Intel 486 (1989) used an improved algorithm that could end early, so multiplying by a small number could take just 9 cycles.
Although these optimizations improved performance, they still depended on looping over the bits. With the shift to 32-bit processors, the loop time became unwieldy. The solution was to replace the loop with hardware: instead of performing 32 shift-and-add loops, an array of adders could compute the multiplication in one step. This quantity of hardware was unreasonable in the 8086 era, but as Moore's law made transistors smaller and cheaper, hardware multiplication became practical. For instance, the Cyrix Cx486SLC (1992) had a 16-bit hardware multiplier that cut word multiply down to 3 cycles. The Intel Core 2 (2006) was even faster, able to complete a 32-bit multiplication every clock cycle.
Hardware multiplication is a fairly complicated subject, with many optimizations to maximize performance while minimizing hardware.14 Simply replacing the loop with a sequence of 32 adders is too slow because the result would be delayed while propagating through all the adders. The solution is to arrange the adders as a tree to provide parallelism. The first layer has 16 adders to add pairs of terms. The next layer adds pairs of these partial sums, and so forth. The resulting tree of adders is 5 layers deep rather than 32, reducing the time to compute the sum. Real multipliers achieve further performance improvements by splitting up the adders and creating a more complex tree: the venerable Wallace tree (1964) and Dadda multiplier (1965) are two popular approaches. Another optimization is the Booth algorithm (1951), which performs signed multiplication directly, without converting the arguments to positive values first. The Pentium 4 (2000) used a Booth encoder and a Wallace tree (ref), but research in the early 2000s found the Dadda tree is faster and it is now more popular.
Conclusions
Multiplication is much harder to compute than addition or subtraction. The 8086 processor hid this complexity from the programmer by providing four multiplication instructions for byte and word multiplication of signed or unsigned values. These instructions implemented multiplication in microcode, performing shifts and adds in a loop. By using microcode subroutines and conditional execution, these four machine instructions share most of the microcode. As the microcode capacity of the 8086 was very small, this was a critical feature of the implementation.
If you made it through all the discussion of microcode, congratulations! Microcode is even harder to understand than assembly code. Part of the problem is that microcode is very fine-grain, with even ALU operations split into multiple steps. Another complication is that 8086 microcode performs a register move and another operation in parallel, so it's hard to keep track of what's going on. Microcode can seem a bit like a jigsaw puzzle, with pieces carefully fit together as compactly as possible. I hope the explanations here made sense, or at least gave you a feel for how microcode operates.
I've written multiple posts on the 8086 so far and plan to continue reverse-engineering the 8086 die so follow me on Twitter @kenshirriff or RSS for updates. I've also started experimenting with Mastodon recently as @[email protected].
Notes and references
-
Mainframes going back to ENIAC had multiply and divide instructions. However, early microprocessors took a step back and didn't supports these more complex operations. (My theory is that the decline in memory prices made it more cost-effective to implement multiply and divide in software than hardware.) The National Semiconductor IMP-16, a 16-bit bit-slice microprocessor from 1973, may be the first with multiply and divide instructions. The 8-bit Motorola 6809 processor (1978) included 8-bit multiplication but not division. I think the 8086 was the first Intel processor to support multiplication. ↩
-
The 8086 also supported division. Although the division instructions are similar to multiplication in many ways, I'm focusing on multiplication and ignoring division for this blog post. ↩
-
My microcode analysis is based on Andrew Jenner's 8086 microcode disassembly. ↩
-
I think
CORXstands forCore MultiplyandCORDstands forCore Divide. ↩ -
The definitions of carry and overflow are different for multiplication compared to addition and subtraction. Note that the result of a multiplication operation will always fit in the available result space, which is twice as large as the arguments. For instance, the biggest value you can get by multiplying 16-bit values is
0xffff×0xffff=0xfffe0001which fits into 32 bits. (Signed and 8-bit multiplications fit similarly.) This is in contrast to addition and subtraction, which can exceed their available space. A carry indicates that an addition exceeded its space when treated as unsigned, while an overflow indicates that an addition exceeded its space when treated as unsigned. ↩ -
The Intel documentation states that the sign, carry, overflow, and parity flags are undefined after the
MULoperation, even though the microcode causes them to be computed. The meaning of "undefined" is that programmers shouldn't count on the flag values because Intel might change the behavior in later chips. This thread discusses the effects ofMULon the flags, and how the behavior is different on the NEC V20 chip. ↩ -
It may be worth explaining why the two's complement of a number is defined by adding 1 to the one's complement. The one's complement of a number simply flips all the bits. If you take a byte value
n,0xff-nis the one's complement, since a 1 bit innproduces a 0 bit in the result.Now, suppose we want to represent -5 as a signed byte. Adding
0x100will keep the same byte value with a carry out of the byte. But0x100- 5 = (1 + 0xff) - 5 = 1 + (0xff- 5) = 1 + (one's complement of 5). Thus, it makes sense mathematically to represent -5 by adding 1 to the one's complement of 5, and this holds for any value. ↩ -
The negation code is a bit tricky because the result is split across two words. In most cases, the upper word is bitwise complemented. However, if the lower word is zero, then the upper word is negated (two's complement). I'll demonstrate with 16-bit values to keep the examples small. The number 257 (0x0101) is negated to form -257 (0xfeff). Note that the upper byte is the one's complement (0x01 vs 0xfe) while the lower byte is two's complement (0x01 vs 0xff). On the other hand, the number 256 (0x0100) is negated to form -256 (0xff00). In this case, the upper byte is the two's complement (0x01 vs 0xff) and the lower byte is also the two's complement (0x00 vs 0x00).
(Mathematical explanation: the two's complement is formed by taking the one's complement and adding 1. In most cases, there won't be a carry from the low byte to the upper byte, so the upper byte will remain the one's complement. However, if the low byte is 0, the complement is 0xff and adding 1 will form a carry. Adding this carry to the upper byte yields the two's complement of that byte.)
To support multi-word negation, the 8086's
NEGinstruction clears the carry flag if the operand is 0, and otherwise sets the carry flag. (This is the opposite from the above because subtractions (includingNEG) treat the carry flag as a borrow flag, with the opposite meaning.) The microcodeNEGoperation has identical behavior to the machine instruction, since it is used to implement the machine instruction.Thus to perform a two-word negation, the microcode negates the low word (tmpC) and updates the flags (
F). If the carry is set, the one's complement is applied to the upper word (tmpA). But if the carry is cleared, the two's complement is applied to tmpA. ↩ -
The
IMULCOFroutine considers the upper half of the result significant if it is not the sign extension of the lower half. For instance, dropping the top byte of0x0005(+5) yields 0x05 (+5). Dropping the top byte of0xfffb(-5) yields 0xfb (-5). Thus, the upper byte is not significant in these cases. Conversely, dropping the top byte of0x00fb(+251) yields0xfb(-5), so the upper byte is significant. ↩ -
Curiously, the 8086 patent states that the
Xregister is a 4-bit register holding bits 3–6 of the byte (col. 9, line 20). But looking at the die, it is a 3-bit register holding bits 3–5 of the byte. ↩ -
Some instructions are specified by bits 5–3 in the ModR/M byte rather than in the first opcode byte. The motivation is to avoid wasting bits for instructions that use a ModR/M byte but don't need a register specification. For instance, consider the instruction
ADD [BX],0x1234. This instruction uses a ModR/M byte to specify the memory address. However, because it uses an immediate operand, it does not need the register specification normally provided by bits 5–3 of the ModR/M byte. This frees up the bits to specify the instruction. From one perspective, this is an ugly hack, while from another perspective it is a clever optimization. ↩ -
Andrew Jenner discusses the F1 flag and the interaction between
REPand multiplication here. ↩ -
Here are some detailed performance numbers. The 8086 processor takes 70–77 clock cycles to multiply 8-bit values and 118–133 clock cycles to multiply 16-bit values. Signed multiplies are a bit slower because of the sign calculations: 80–98 and 128–154 clock cycles respectively. The time is variable because of the conditional jumps in the multiplication process.
The Intel 186 (1982) optimized multiplication slightly, bringing the register word multiply down to 35–37 cycles. The Intel 286 (also 1982) reduced this to 21 clocks. The 486 (1989) used a shift-add multiply function but it had an "early out" algorithm that stopped when the remaining bits were zero, so a 16-bit multiply could take from 9 to 22 clocks. The 8087 floating point coprocessor (1980) used radix-4 multiplication, multiplying by pairs of bits at a time and either adding or subtracting. This yields half the addition cycles. The Pentium's P5 micro-architecture (1993) took the unusual approach of reusing the floating-point unit's hardware multiplier for integer multiplication, taking 10 cycles for a 32-bit multiplication. ↩
-
This presentation gives a good overview of implementations of multiplication in hardware. ↩