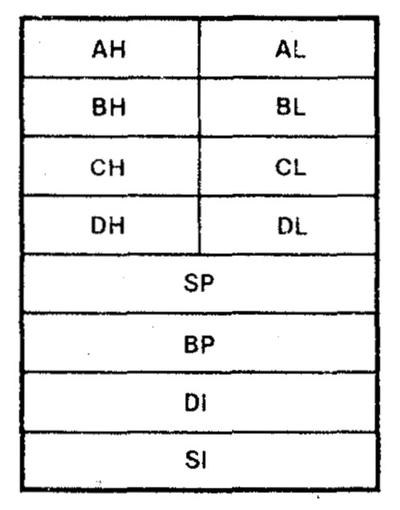
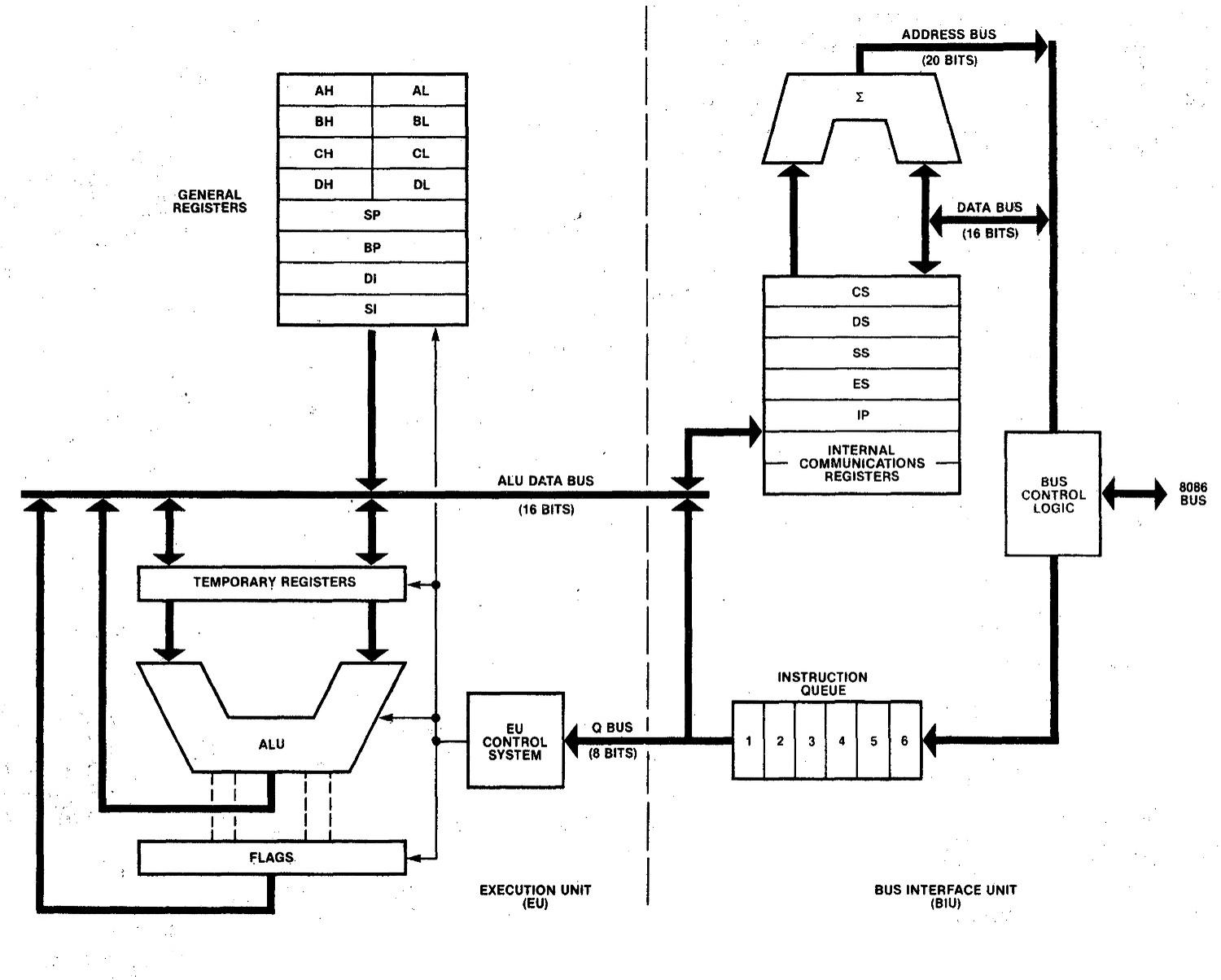
The Intel 8086 processor contains many interesting components that can be understood through reverse engineering. In this article, I'll discuss the adder that is used for address calculations. The photo below shows the tiny silicon die of the 8086 processor under a microscope. The left part of the chip has the 16-bit datapath including the registers and the Arithmetic-Logic Unit (ALU); you can see the pattern of circuitry repeated 16 times. The rectangle in the lower-right is the microcode ROM, defining the execution of each instruction.
The 16-bit adder, the topic of this post, is in the upper left. The magnified view shows how the adder is constructed from 16 stages, one for each bit. The upper row handles the top bits (15-8) and the lower row handles the low bits (7-0).1 Studying the die reveals how this 16-bit adder was optimized through clever circuit design, specialized logic gates, and careful layout techniques.
How the adder is used in the 8086
You might wonder why the 8086 contains both an adder and an ALU (arithmetic-logic unit). The reason is that the adder is used for address calculations, while the ALU is used for data calculations. The 8086 prefetches instructions using a "Bus Interface Unit", which runs semi-independently from the "Execution Unit" that executed instructions. It would have been difficult for the Bus Interface Unit and the Execution Unit to share the ALU without conflicts. By providing both an adder2 and the ALU, the two calculations can take place in parallel.
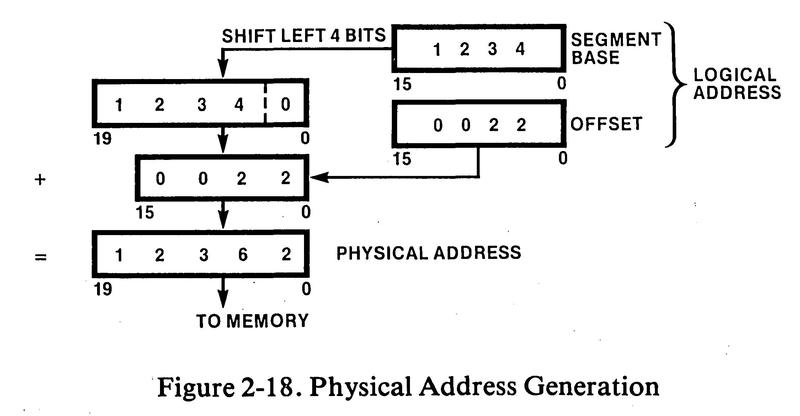
Microprocessors of the early 1970s typically had 16-bit addresses, capable of accessing 64 kilobytes of memory. At first, 64 kilobytes seemed like more memory than anyone would need (or afford), but as the price of memory chips plunged, the demand for memory grew.4 To support a larger address space, Intel added segment registers to the 8086, a hack that allowed the processor to access a megabyte of memory but led to years of gnashed teeth. The concept is to break memory into 64-kilobyte segments. A segment register specifies the start of the memory segment, and a 16-bit address indicates an address within that segment. These are combined in the adder, as shown below, to obtain the memory address. One downside is that accessing regions of memory larger than 64 kilobytes is difficult; the segment register must be modified to get outside the current segment.3
How does the 16-bit adder compute a 20-bit address? The trick is that since the segment register is shifted 4 bits, the adder sums the 16 bits of the segment register and the top 12 bits of the offset. The four low bits of the offset bypass the adder since they are unchanged. For other purposes (such as incrementing the instruction counter), the adder operates on unshifted 16-bit addresses. Thus, the register circuitry has logic to feed either shifted or non-shifted values to the adder.
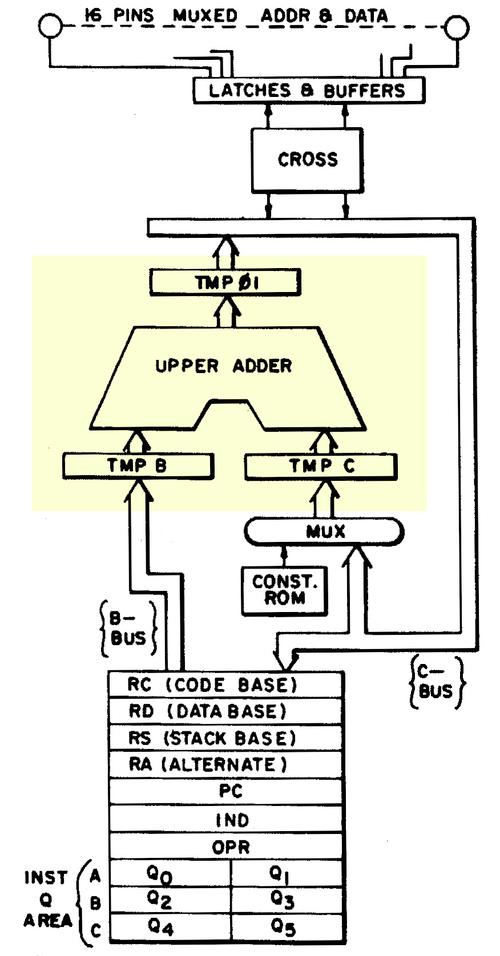
The diagram below, from the 8086 patent, shows how the adder sits between the segment registers and the address pins, computing the address. In the patent, the segment registers were named RC, RD, RS, and RA, not their current names: CS, DS, SS, and ES.
The adder implementation
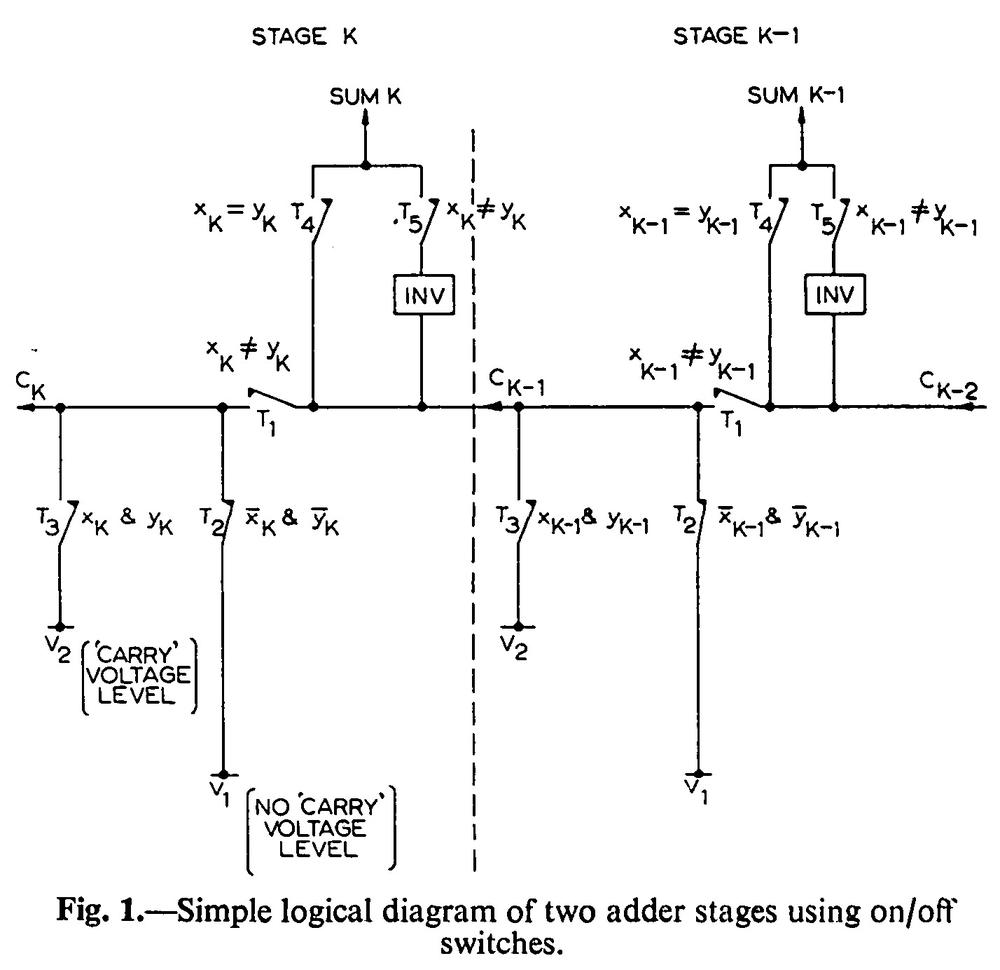
If you've studied digital logic, you may be familiar with the full adder, a building-block for adding binary numbers. Specifically, a full adder takes two bits and a carry-in bit. It adds these three bits and outputs the 1-bit sum, as well as a carry-out bit. (For instance 1+0+1 = 10 in binary, so the carry-out is 1 and the sum bit is 0.) A 16-bit adder can be created by joining 16 full-adders, with the carry-out from one feeding into the carry-in of the next. Just as you add two decimal numbers, moving carries to the next column on the left, each full adder adds one column in the binary numbers, and the carry is passed on to the left.
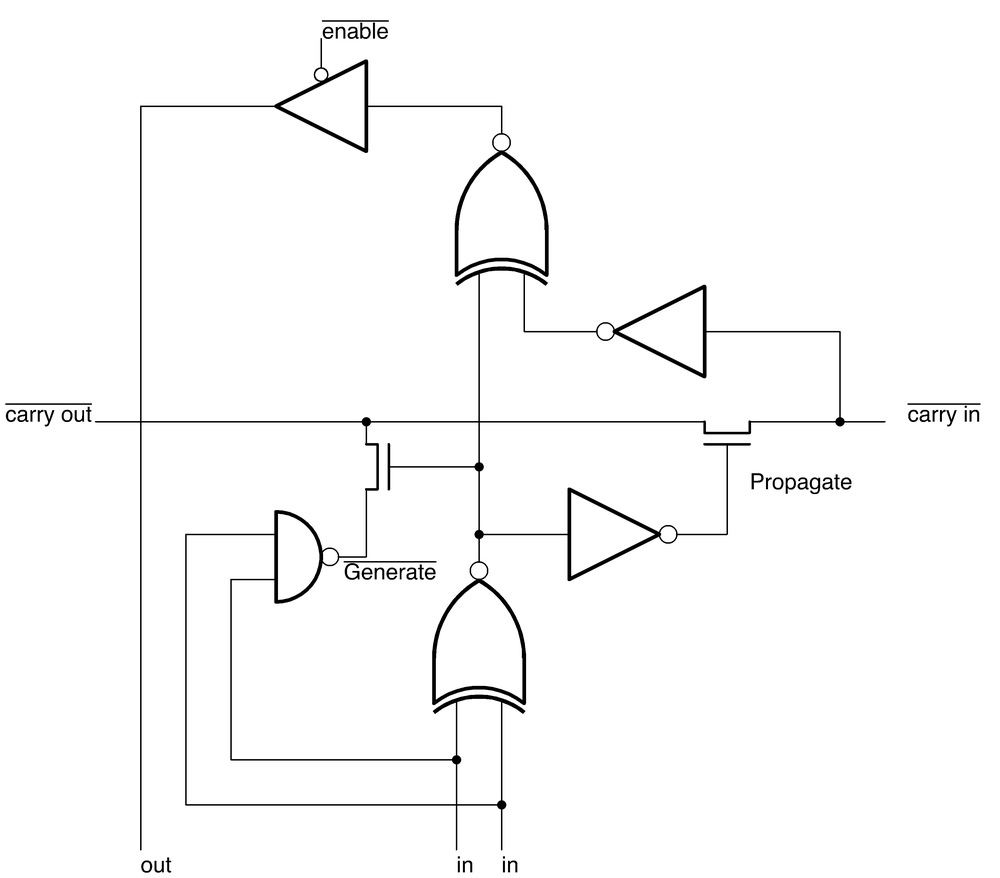
A full adder can be implemented in different ways; the 8086's circuit is shown below. (This circuit is repeated 16 times in the 16-bit adder.) Each adder stage takes two inputs (at the bottom) and the carry-in (inverted, at the right). These are summed to form a 1-bit sum output (bottom) and a carry-out (at the left). The sum bit is formed by the two exclusive-NOR gates that combine the two inputs and the carry-in.5 The output passes through a tri-state buffer (at the top), allowing it to be connected to an internal data bus.6
The carry computation uses an optimization called the Manchester carry chain7, dating back to 1959. The problem with addition is carries are slow; in the straightforward approach, each bit sum can't be computed until the carry to the right has been computed. (Similar to computing 99999999+1 with long addition; each digit requires you to carry the one.) If each bit must wait for the previous carry, addition becomes a slow, serial process.
The idea behind the Manchester carry chain is to decide, in parallel, if each stage will generate a carry, propagate an existing carry, or block any carry. Then, the carry can rapidly flow through the "carry chain" without sequential evaluation. To understand this, consider the cases when adding two bits and a carry-in. For 0+0, there will be no carry, regardless of any carry-in. On the other hand, adding 1+1 will always produce a carry, regardless of any carry-in; this case is called "carry generate". The interesting cases are 0+1 and 1+0; there will be a carry-out if there was a carry-in. This case is called "carry propagate" since the carry-in propagates through the stage unchanged.
The "carry generate" and "carry propagate" signals are used to open or close switches (i.e. transistors) in the carry line. For "carry propagate", carry-in is connected to carry-out, so the carry can flow through. Otherwise, the incoming carry is disconnected. For "carry generate", a carry signal is sent to carry-out. Since these switches can all be set in parallel, carry computation is quick. There is still some propagation delay as the carry-in flows through the switches, potentially from bit 0 all the way to bit 15, but this is much faster than computing the carry through a sequence of logic gates.
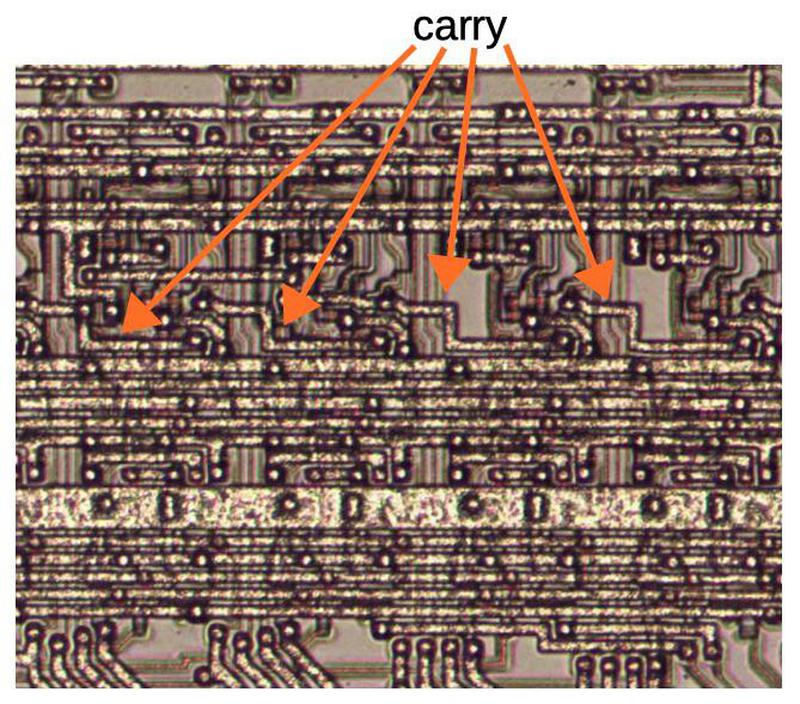
The carry chain is visible on the die; the photo above shows four stages of the adder. The horizontal lines are the metal wiring: control signals, ground, and power (the thick line near the bottom). The silicon circuitry is barely visible underneath the metal. The carry chain wires are interrupted at each stage, to connect to the transistors underneath, and the new carry continues on to the next stage.
Carry-skip
Careful examination of the adder shows that while the 16 single-bit stages are very similar, they are not all identical. The extra circuitry indicated below turns out to be a performance optimization called the carry-skip adder.
The idea of carry-skip is to skip over some of the stages in the carry chain if possible, reducing the worst-case delay through the chain. For example, if there is a carry-in to bit 8, and the carry propagate is set for bits 8, 9, 10, and 11, then it can be immediately determined that there is a carry-in to bit 12. Thus, by ANDing together the carry-in and the four carry-propagate values, the carry-in to bit 12 can be calculated immediately for this case. In other words, the carry skips from bit 8 to bit 12. Likewise, similar carry-skip circuits allow the carry to skip from bit 2 to bit 4, and bit 4 to bit 8. These carry-skip circuits reduced the adder's worst-case computation time.8
Regular logic vs dynamic logic
The performance of the adder is critical to the overall speed of the 8086, so it uses some interesting techniques to implement fast logic gates. Some of the adder's gates are built with dynamic logic. A standard logic gate is straightforward: you put signals in and you get the result out. In contrast, a dynamic logic gate uses a periodic clock signal to compute the logic function.9 Since dynamic logic can be faster and more compact, it is used in modern processors, in the form of domino logic.
Dynamic logic depends on a two-phase clock, commonly used for timing in microprocessors of that era. The two-phase clock consists of two clock signals that are active in alternation. First, phase 1 (ɸ1) is high and phase 2 (ɸ2) is low. Then phase 1 is low and phase 2 is high. This cycle repeats at the clock frequency, such as 5 MHz.
The schematic below shows a dynamic NAND gate from the adder. In phase 1, the clock ɸ1 turns on the lower transistor, pulling the input to the inverter low. Phase 2 is the evaluation phase, where the logic function is computed. If both inputs are high, the two input transistors will turn on, allowing clock ɸ2 to pass through to the inverter input, pulling it high and causing the output to be low. On the other hand, if either input is low, the clock ɸ2 cannot pass through the transistors. Instead, the inverter input remains low from the previous phase, due to the stray capacitance of the wire, so the output is high. Thus, in either case, the circuit implements the NAND functionality, with a low output only if the inputs are both high. Note that unlike a standard logic gate, the dynamic logic gate's output is only valid during clock phase 2.
The diagram below shows how the dynamic NAND gate is physically implemented on the die; the layout of the schematic corresponds to the physical layout. In the photo, the metal layer has been removed, showing the silicon underneath. The yellowish regions are doped, conductive silicon. The brownish, metallic lines are polysilicon, a special type of silicon used as wiring. A transistor is formed when polysilicon crosses doped silicon; the polysilicon is the gate, controlling conduction between the silicon on either side. The transistors have complex, twisted shapes to fit the circuitry in as little space as possible. Each transistor was given a particular size for the best balance between speed and power consumption. For example, the input transistors are small, while the inverter transistor is much larger.
The diagram below shows the location of a NAND gate in the 8086 chip. The first box zooms in on one of the 16 single-bit adder circuits. The second box shows the position of the NAND gate within the adder. The NAND gate is almost visible in the overall die photo showing how large the features are, compared to a modern chip.
Another interesting dynamic logic gate in the adder is exclusive-NOR (XNOR, the complement of XOR), which outputs 1 if both inputs are the same, and 0 otherwise. The schematic below shows the implementation of XNOR.10 As before, during phase 1, the inverter input is pulled to ground. In the evaluation phase, clock ɸ2 can pull the inverter input high through either the upper pair of transistors or the lower pair of transistors. This will happen if the inputs are different (input 2 is high and input 1 is low, or if input 1 is high and input 2 is low), causing the inverter output to be low. Otherwise, the inverter input will remain low from phase 1, and the inverter output will be high. Thus, the output is high if the two inputs are equal, and low otherwise, the desired XNOR behavior.
Conclusions
The adder in the 8086 has a critical role, computing addresses for every memory access. A 16-bit adder may seem like a straightforward circuit, but the adder in the 8086 was highly optimized so it wouldn't be a performance bottleneck. To speed up carry processing, the adder uses a Manchester carry chain, with carry-skip circuitry on top of that. The adder uses three different designs for logic gates: standard NMOS gates, pass-transistor logic, and dynamic logic. Even at the transistor level, the circuit is highly optimized, with transistors of all shapes and sizes carefully packed together.
The Intel 8086 is an interesting processor with complex circuits but still simple enough that its circuits can be studied under a microscope. The 8086 has 29,000 transistors and features that are a few micrometers large. In comparison, modern processors have billions of transistors and transistors that are measured in nanometers. While the progress of Moore's law has yielded great improvements in modern processors, the processors of the 1970s are much better for reverse engineering.
If you're interested in the 8086, I wrote about the 8086 die, its die shrink process and the 8086 registers earlier. I plan to write more about the 8086 so follow me on Twitter @kenshirriff or RSS for updates.
Notes and references
-
The adder's layout has bits 15-8 in the top and bits 7-0 below. This layout is a consequence of the bit ordering in the data path: the bits are interleaved 15-7-14-6-...-8-0, instead of linearly 15-14-...-0. The reason behind this interleaving is that it makes it easy to swap the two bytes in the 16-bit word, by swapping pairs of bits. The adder is split into two rows so it fits into the horizontal space available. Even with the tall, narrow layout of an adder stage, a bit of the adder is wider than a bit of the register file. Splitting the adder into two rows keeps the bit spacing approximately the same, avoiding long wires between the register file and the adder. ↩
-
Many early microprocessors (such as the 6502 and Z-80) had an incrementer for the program counter, separate from the ALU. (One motivation was the ALU was 8 bits while the program counter was 16 bits.) The 68000 had address adders, separate from the ALU. ↩
-
The 8086's segmented architecture led to programming with near pointers and far pointers. A near pointer was a 16-bit pointer that could be held in a register and manipulated easily, but couldn't access more than 64 kilobytes. A far pointer was the combination of an offset and a segment value, resulting in a pointer that could access the full memory but required twice the storage for each pointer. Comparing far pointers was problematic, since they were not unique; multiple offset/segment combinations could address the same physical memory address. ↩
-
In contrast to the 8086, the Motorola 68000 microprocessor (1979) had 32-bit registers. Its address bus was 24 bits wide, allowing it to access 16 megabytes of memory directly, without segment registers. The 68020 (1984) extended the address bus to 32 bits, allowing 4 gigabytes of memory to be accessed.
The 68000 was provided in a 64-pin package, providing plenty of pins for the 24 address lines and 16 data lines. In comparison, Intel didn't like large IC packages and used a 40-pin package for the 8086. As a result, the 8086 used 20 pins for the address lines, and reused (i.e. multiplexed) 16 of these pins for data lines. The 8086 also multiplexed many of the control pins, complicating system design. ↩
-
The desired sum output is input1⊕input2⊕carry-in. In the 8086 adder, the carry-in is inverted, there are two exclusive-NOR gates, and an inverter in the path. Thus, the circuit has four inversions in total; since this number is even, they cancel out and the circuit produces the desired exclusive-OR of the three values. ↩
-
A tri-state buffer has three different outputs: high (1), low (0), or high-impedance (hi-Z). In the hi-Z state, the buffer is not outputting anything and is electrically disconnected. The motivation for this is that multiple signals can be connected to a bus through tri-state buffers. By enabling one buffer and disabling the rest, the desired signal can be output to the bus. (Regular buffers wouldn't work because electrical problems would arise if one buffer outputs a 1 and another outputs a 0.) Open-collector outputs are an alternative for connecting multiple signals to a bus. ↩
-
The Manchester carry chain was developed by the University of Manchester and described in the article Parallel addition in digital computers: a new fast 'carry' circuit, 1959. It was used in the Atlas supercomputer (1962).
The original diagram showing how the Manchester carry chain is implemented, from 1959.The diagram above, from the original article, shows the structure of the Manchester carry chain. Although the switches look like relay contacts, the carry chain was implemented with transistors (2N501 micro-alloy diffused-base transistors). The structure of the carry chain in the 8086 is similar to the diagram above, but the top switches are replaced by XNOR gates. ↩
-
A few notes on the carry-skip implementation. Conceptually the signals are ANDed together, but the implementation uses a NOR gate since the carry and propagate signal inputs are inverted. For carry-skip to be useful, computing the carry with a gate must be faster than the carry chain, which was achieved by skipping four stages at a time. (I don't know why the first stage was implemented with a smaller skip.) Note that carry-skip helps in specific cases (which include the worst-case), so the regular carry circuitry is still required. ↩
-
Processors always have a maximum clock speed, the fastest they can run. (The original 8086 ran at up to 5 MHz, while the later 8086-1 supported 10 MHz.) However, due to the use of dynamic logic, the 8086 also had a minimum clock speed of 2 MHz. If the clock ran slower than that, there was a risk of the charge on a wire leaking away before it was used, causing errors. ↩
-
Surprisingly, the adder uses a completely different implementation for the upper XNOR gate; it is implemented with pass-transistor logic rather than dynamic logic. I think the motivation is that the carry-in signal to these XNOR gates is not quite synchronous, due to propagation delay through the carry chain. Dynamic logic has the disadvantage that if an input signal switches low after the clock, the gate can't recover; the circuit has been charged and won't be discharged until the next clock phase. In particular, if a carry comes in after clock phase 2 has started, it can't switch the output high. By using non-dynamic logic, the output will switch correctly when the carry arrives, even if it is not aligned with the clock.
Pass-transistor logic is different from "regular" NMOS logic gates, but provides a more efficient way of implementing XNOR. The circuit is similar to the XNOR in the Z-80 microprocessor, which I've described earlier, so I won't go into more detail here.
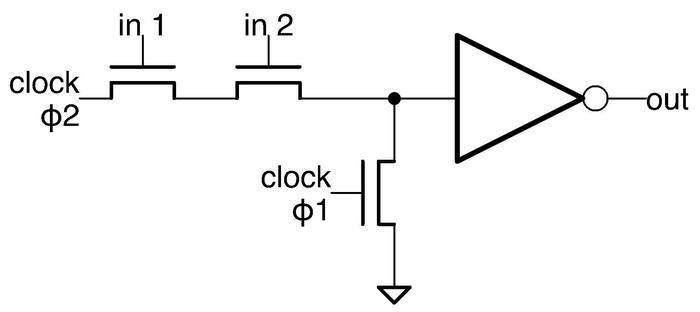
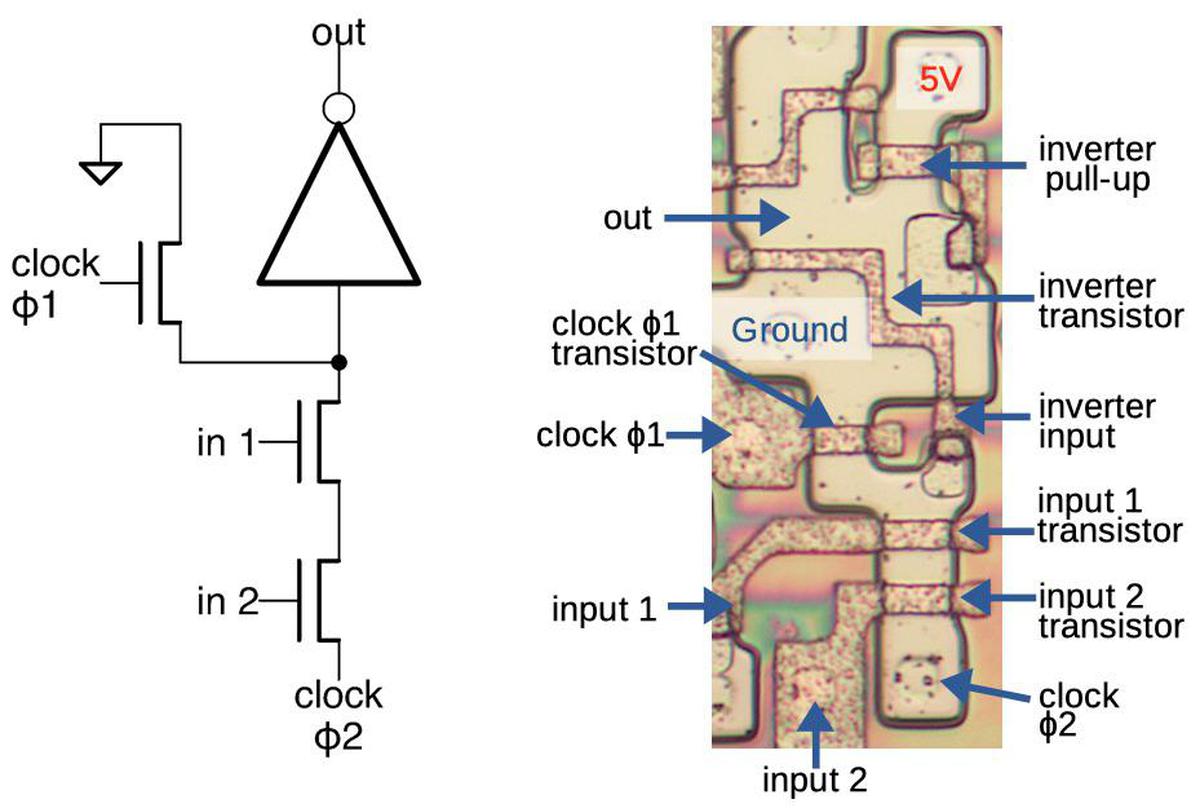
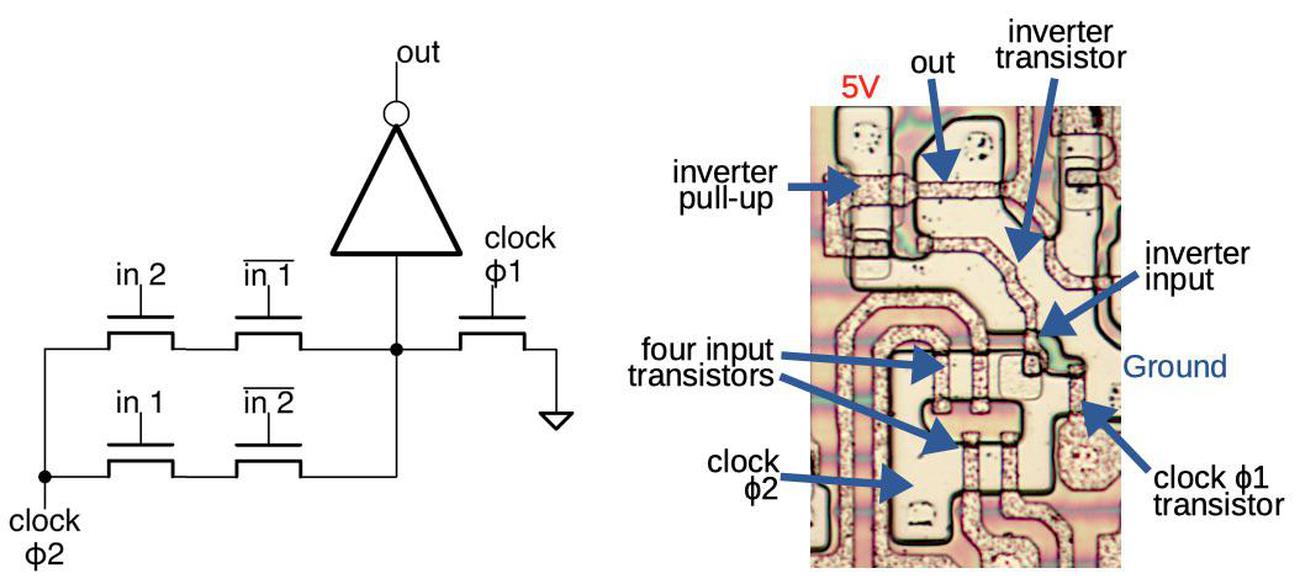
Pass-transistor logic is also used to implement the input and output latches on the adder. On the patent diagram shown earlier, these latches appear as "TMP B" and "TMP C" on the input side of the adder and "TMP ɸ1" on the output side. These latches are necessary because otherwise the adder's output would be connected directly to the input, causing the adder to repeatedly add. The implementation of these latches is simply clocked pass transistors in the path, holding the value by capacitance. ↩