I recently received an interesting math problem: how many 12-digit numbers can you make from the digits 1 through 5 if each digit must appear at least once. The problem seemed trivial at first, but it turned out to be more interesting than I expected, so I'm writing it up here. I was told the problem is in a book of Schrodinger's, but I don't know any more details of its origin.
(The problem came to me via Aardvark (vark.com), which is a service where you can send questions to random people, and random people send you questions. Aardvark tries to match up questions with people who may know the answer. I find it interesting to see the questions I receive.)
The brute force solution
I didn't see any obvious solution to the problem, so I figured I'd first use brute force. I didn't use the totally brute force solution - enumerating all 12 digit sequences and counting the valid ones - since it would be pretty slow, so I took a slightly less brute force approach.
If 1 appears a times, 2 appears b times, and 3, 4, and 5 appear c, d, and e times, then the total number of possibilities is 12!/(a!b!c!d!e!) - i.e. the multinomial coeffient.
Then we just need to sum across all the different combinations of a through e. a has to be at least 1, and can be at most 8 (in order to leave room for the other 4 digits). Then b has to be at least 1 and at most 9-a, and so on. Finally, e is whatever is left over.
The Python code is straightforward, noting that range(1, 9) counts from 1 to 8:
from math import factorial
total = 0
for a in range(1, 8+1):
for b in range(1, 9-a+1):
for c in range(1, 10-a-b+1):
for d in range(1, 11-a-b-c+1):
e = 12-a-b-c-d
total += (factorial(12) / factorial(a) / factorial(b)
/ factorial(c) / factorial(d) / factorial(e))
print total
Or, in Arc:
(def factorial (n)
(if (<= n 1) 1
(* n (factorial (- n 1)))))
(let total 0
(for a 1 8
(for b 1 (- 9 a)
(for c 1 (- 10 a b)
(for d 1 (- 11 a b c)
(let e (- 12 a b c d)
(++ total (/ (factorial 12) (factorial a) (factorial b)
(factorial c) (factorial d) (factorial e))))))))
total)
Either way, we quickly get the answer 165528000.
The generalized brute force solution
The above solution is somewhat unsatisfying, since if we want to know how many 11 digits numbers can be made from at least one of 1 through 6, for instance, there's no easy way to generalize the code.
We can improve the solution by writing code to generate the vectors of arbitrary digits and length. In Python, we can use yield, which magically gives us the vectors one at a time. The vecs function recursively generates the vectors that sum to <= t. The solve routine adds the last entry in the vector to make the sum exactly equal the length. My multinomial function is perhaps overly fancy, using reduce to compute the factorials of all the denominator terms and multiply them together in one go.
from math import factorial
# Generate vectors of digits of length n with sum <= t, and minimum digit 1.
def vecs(n, t):
if n <= 0:
yield []
else:
for vec in vecs(n-1, t-1):
for last in range(1, t - sum(vec) + 1):
yield vec + [last]
def multinomial(n, ks):
return factorial(n) / reduce(lambda prod, k: prod * factorial(k), ks, 1)
# Find number of sequences of digits 1 to n, of length len,
# with each digit appearing at least once
def solve(n, len):
total = 0
for vec0 in vecs(n-1, len-1):
# Make the vector of length n summing exactly to len
vec = vec0 + [len - sum(vec0)]
total += multinomial(len, vec)
return total
Now,
solve(5, 12) solves the original problem, and we can easily solve related problems.
In Arc, doing yield would need some crazy continuation code, so I just accumulate the list of vectors with accum and then process it. The code is otherwise similar to the Python code:
(def vecs (n t)
(if (<= n 0) '(())
(accum accfn
(each vec (vecs (- n 1) (- t 1))
(for last 1 (- t (reduce + vec))
(accfn (cons last vec)))))))
(def multinomial (n ks)
(/ (factorial n) (reduce * (map factorial ks))))
(def solve (n len)
(let total 0
(each vec0 (vecs (- n 1) (- len 1))
(++ total (multinomial len
(cons (- len (reduce + vec0)) vec0))))
total))
This solution will solve our original problem quickly, but in general it's exponential, so solving something like n = 10 and length = 30 gets pretty slow.
The dynamic programming solution
By thinking about the problem a bit more, we can come up with a simpler solution. Let's take all the sequences of 1 through 5 of length 12 with each number appearing at least once, and call this value
S(5, 12). How can we recursively find this value? Well, take a sequence and look at the last digit, say 5. Either 5 appears in the first 11 digits, or it doesn't. In the first case, the first 11 digits form a sequence of 1 through 5 of length
11 with each number appearing at least once. In the second case, the first 11 digits form a sequence of 1 through
4 of length
11 with each number appearing at least once. So we have S(5, 11) sequences of the first case, and S(4, 11) of the second case. We assumed the last digit was a 5, but everything works the same if it was a 1, 2, 3, or 4; there are 5 possibilities for the last digit.
The above shows that S(5, 12) = 5 * (S(5, 11) + S(4, 11)). In general, we have the nice recurrence S(n, len) = n * (S(n, len-1) + S(n-1, len-1)). Also, if you only have a single digit, there's only one solution, so S(1, len) = 1. And if you have more digits than length to put them in, there are clearly no solutions, so S(n, len) = 0 if n > len. We can code this up in a nice recursive solution with memoization:
memo = {}
def solve1(digits, length):
if memo.has_key((digits, length)):
return memo[(digits, length)]
if digits > length:
result = 0
elif digits == 1:
result = 1
else:
result = digits * (solve1(digits-1, length-1) + solve1(digits, length-1))
memo[(digits, length)] = result
return result
An interesting thing about this solution is it breaks down each function call into two simpler function calls. Each of these turns into two simpler function calls, and so forth, until it reaches the base case. This results in an exponential number of function calls. This isn't too bad for solving the original problem of length 12, but the run time rapidly gets way too slow.
Note that the actual number of different function evaluations is pretty small, but the same ones keep getting evaluated over and over exponentially often. The traditional way of fixing this is to use dynamic programming. In this approach, the structure of the algorithm is examined and each value is calculated just one, using previously-calculated values. In our case, we can evaluate S(1, 0), S(2, 0), S(3, 0), and so on. Then evaluate S(2, 1), S(2, 2), S(2, 3) using those values. Then evaluate S(3, 2), S(3, 3), and so on. Note that each evaluation only uses values that have already been calculated. For an introduction to dynamic programming, see Dynamic Programming Zoo Tour.
Rather than carefully looping over the sub-problems in the right order to implement a dynamic programming solution, it is much easier to just use memoization. The trick here is once a subproblem is solved, store the answer. If we need the answer again, just use the stored answer rather than recomputing it. Memoization is a huge performance win. Without memoization solve1(10, 30) takes about 15 seconds, and with it, the solution is almost immediate. (solve1 10 35) takes about 80 seconds.
The Arc implementation is nice, because defmemo creates a function that is automatically memoized.
(defmemo solve1 (digits length)
(if (> digits length) 0
(is digits 1) 1
(* digits (+ (solve1 (- digits 1) (- length 1))
(solve1 digits (- length 1))))))
A faster dynamic programming solution
When trying to count the number of things satisfying a condition, it's often easier to figure out how many
don't satisfy the condition. We can apply that strategy to this problem. The total number of 12-digit sequences made from 1 through 5 is obviously 5^12. We can just subtract the number of sequences that are missing one or more digits, and we get the answer we want.
How many sequences are missing 1 digit? S(4, 12) is the number of sequences containing at least one of 1 through 4, and by definition missing the digit 5. Of course, we need to consider sequences missing 4, 3, 2, or 1 as well. Likewise, there are S(4, 12) of each of these, so 5 * S(4, 12) sequences missing exactly one digit.
Next, sequences missing exactly 2 of the digits 1 through 5. S(3, 12) is the number of sequences containing at least one of 1 through 3, so they are missing 4 and 5. But we must also consider sequences missing 1 and 2, 1 and 3, and so on. There are 5 choose 2 pairs of digits that can be missing. Thus in total, (5 choose 2) * S(3, 12) sequences are missing exactly 2 of the digits.
Likewise, the number of sequences missing exactly 3 digits is (5 choose 3) * S(2, 12). The number of sequences missing exactly 4 digits is (5 choose 4) * S(1, 12). And obviously there are no sequences missing 5 digits.
Thus, we get the recurrence S(5, 12) = 5^12 - 5*S(4, 12) - 10*S(3, 12) - 10*S(2, 12) - 5*S(1, 12)
In general, we get the recurrence:
 = d^l - \sum_{i=1}^{d-1} \binom{n}{i} S(i,l) "S(d, l) = d^l - \sum_{i=1}^{d-1} \binom{n}{i} S(i,l)")
The same dynamic programming techniques and memoization can be applied to this. Note that the subproblems all have the same length, so there are many fewer subproblems than in the previous case. That is, instead of a 2-dimensional grid of subproblems, the subproblems are all in a single row.
In Python, the solution is:
memo = {}
def solve2(digits, length):
if memo.has_key((digits, length)):
return memo[(digits, length)]
if digits > length:
result = 0
elif digits == 1:
result = 1
else:
result = digits**length
for i in range(1, digits):
result -= sol2(i, length)*choose(digits, i)
memo[(digits, length)] = result
return result
And in Arc, the solution is similar. Instead of looping, I'm using
a map and reduce just for variety. That is, the square brackets define
a function to compute the choose and solve term. This is mapped over the range 1 to digits-1. Then the results are summed with
reduce. As before,
defmemo is used to memoize the results.
(def choose (m n)
(/ (factorial m) (factorial n) (factorial (- m n))))
(defmemo solve2 (digits length)
(if (> digits length) 0
(is digits 1) 1
(- (expt digits length)
(reduce +
(map [* (choose digits _) (solve2 _ length)]
(range 1 (- digits 1)))))))
The mathematical exponential generating function solution
At this point, I dug out my old combinatorics textbook to figure out how to solve this problem. By using exponential
generating functions and a bunch of algebra, we obtain a fairly tidy answer to the original problem:
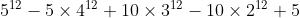
Since the mathematics required to obtain this answer is somewhat complicated, I've written it up separately in
Part II.
Discussion
This problem turned out to be a lot more involved than I thought. It gave me the opportunity to try out some new things in Python and Arc, and make use of my fading knowledge of combinatorics and generating functions.
The Python and Arc code was pretty similar. Python's yield construct was convenient. Arc's automatic memoization was also handy. On the whole, both languages were about equally powerful in solving these problems.
Acknowledgement: equations created through CodeCogs' equation editor
As he described in the talk, he
gives a 
I've been experimenting with IPv6 on my home network. In 
You may have heard that the Internet is