The Yamaha DX7 digital synthesizer (1983) was the classic synthesizer in 1980s pop music.
It uses two custom digital chips to generate sounds with a technique called FM synthesis,
producing complex, harmonically-rich sounds.
Each note was implemented with one of 32 different patterns of modulation and summing, called algorithms.
In this blog post, I look inside the sound chip and explain how the algorithms were implemented.

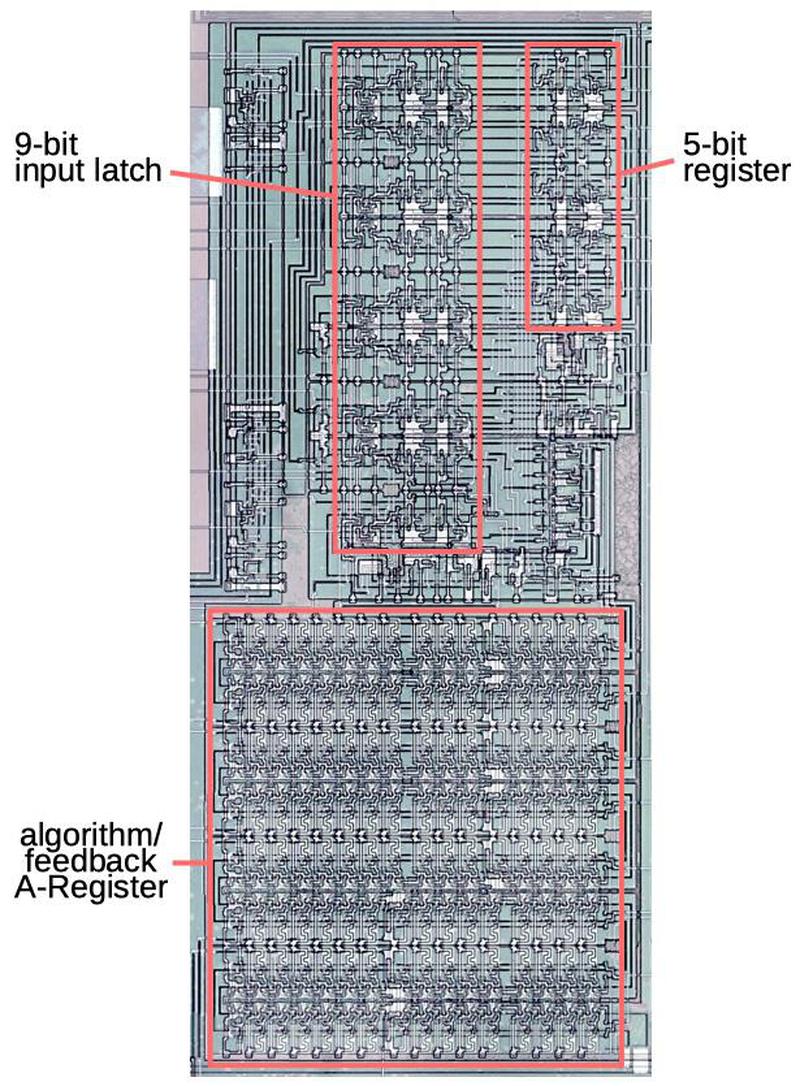
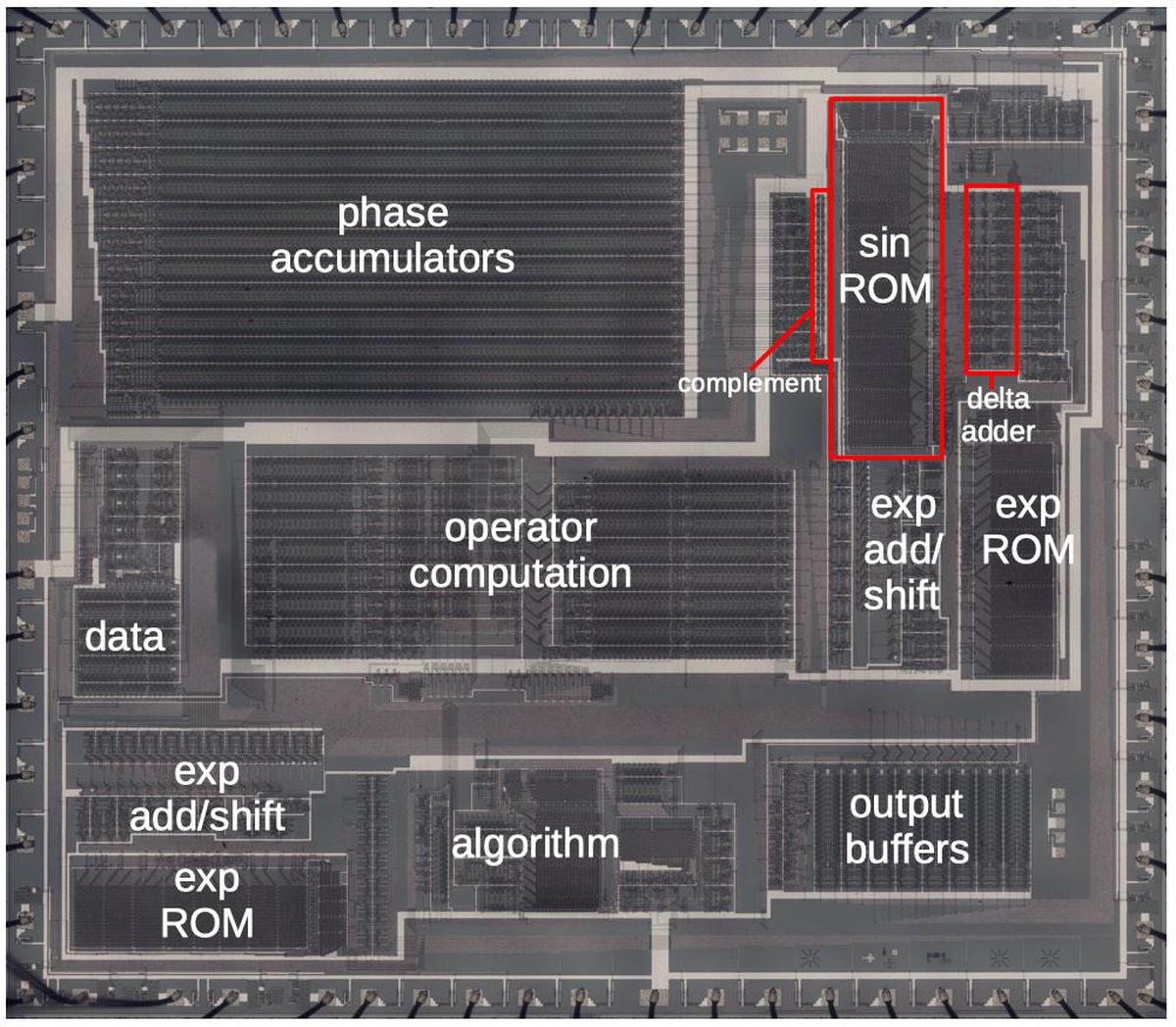
Die photo of the YM21280 chip with the main functional blocks labeled. Click this photo (or any other) for a larger version.
The die photo above shows the DX7's OPS sound synthesis chip under the microscope, showing its complex silicon circuitry.
Unlike modern chips, this chip has just one layer of metal, visible as the whitish lines on top.
Around the edges, you can see the 64 bond wires attached to pads; these connect the silicon die to the chip's 64 pins.
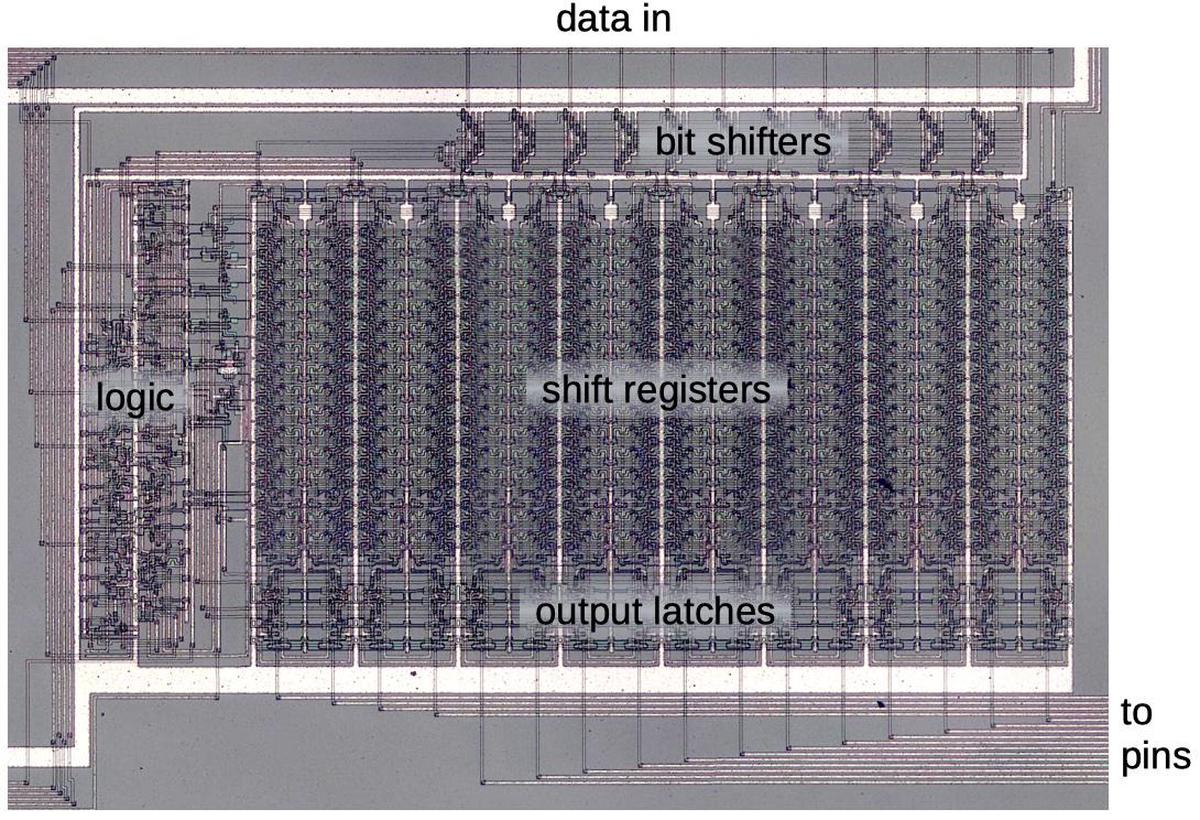
In this blog post, I'm focusing on the highlighted functional blocks: the operator computation circuitry that combines the oscillators, and the algorithm ROM that defines
the different algorithms.
I'll outline the other functional blocks briefly.
Each of the 96 oscillators has a phase accumulator used to generate the frequency.
The sine and exponential functions are implemented with lookup tables in ROMs.
Other functional blocks apply the envelope, hold configuration data, and buffer the output values.
The DX7 was the first commercially successful digital synthesizer, using a radically new way of generating sounds.
Instead of the analog oscillators and filters of an analog synthesizer, the DX7 generates sounds digitally, using a technique called FM synthesis.
The idea is that you start with a sine wave (the carrier signal) and perturb it with another signal (the modulating signal). The modulating signal changes the phase (and thus the frequency) of the carrier, creating complex harmonic structures.
The custom chips inside the DX7 made this possible at an affordable price.

FM synthesis
I'll briefly explain how FM synthesis is implemented.1
The DX7 supports 16 simultaneous notes, with 6 operators (oscillators) for each note, 96 oscillators in total.
However, to minimize the hardware requirements, the DX7 only has a single digital oscillator circuit.
This circuit calculates each operator individually, in sequence. Thus, it takes 96 clock cycles to update all the sounds.
To keep track of each oscillator, the DX7 stores 96 phase values, an index into the sine wave table.
By incrementing the index at a particular rate, a sine wave is produced at the desired frequency.
The idea of FM synthesis is to modulate the index into the sine wave table; by perturbing the index, the output sine wave is modified.
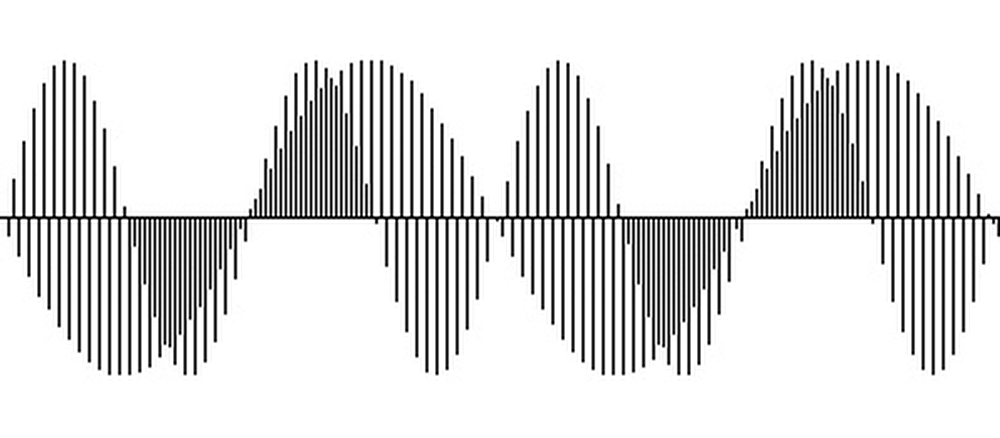
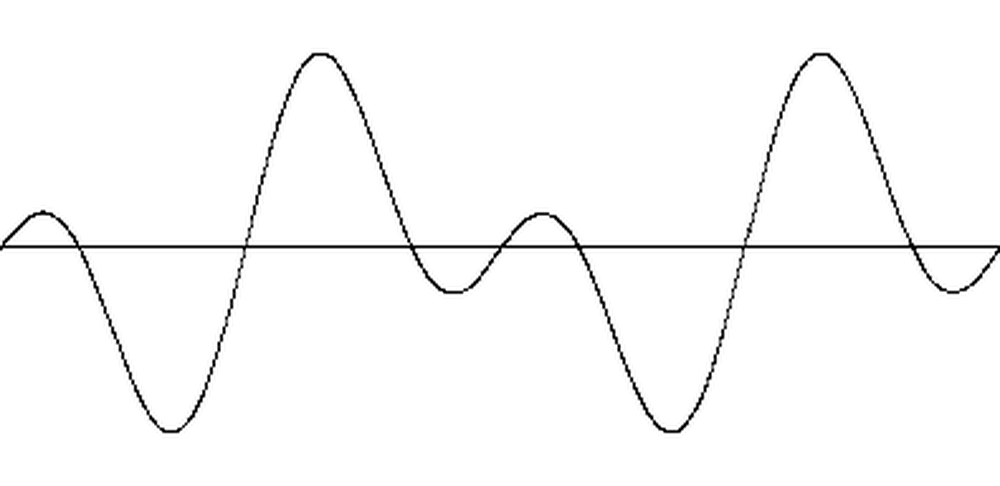
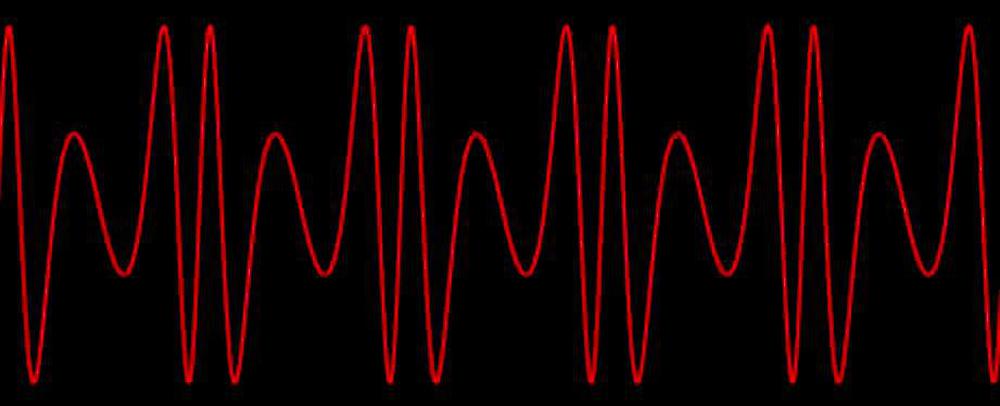
The diagram below shows the effects of modulation.
The top curve shows a sine wave, generated by stepping through the sine wave table at a fixed rate.
The second curve shows the effects of a small amount of modulation, perturbing the index into the table. This distorts the sine wave, compressing and stretching it.
The third curve shows the effects of a large amount of modulation. The index now sweeps back and forth across the entire table, distorting the sine wave unrecognizably.
As you can see, modulation can produce very complex waveforms.
These waveforms have a rich harmonic structure, yielding the characteristic sound of the DX7.
(I made a webpage here where you can experiment with the effects of modulation.)
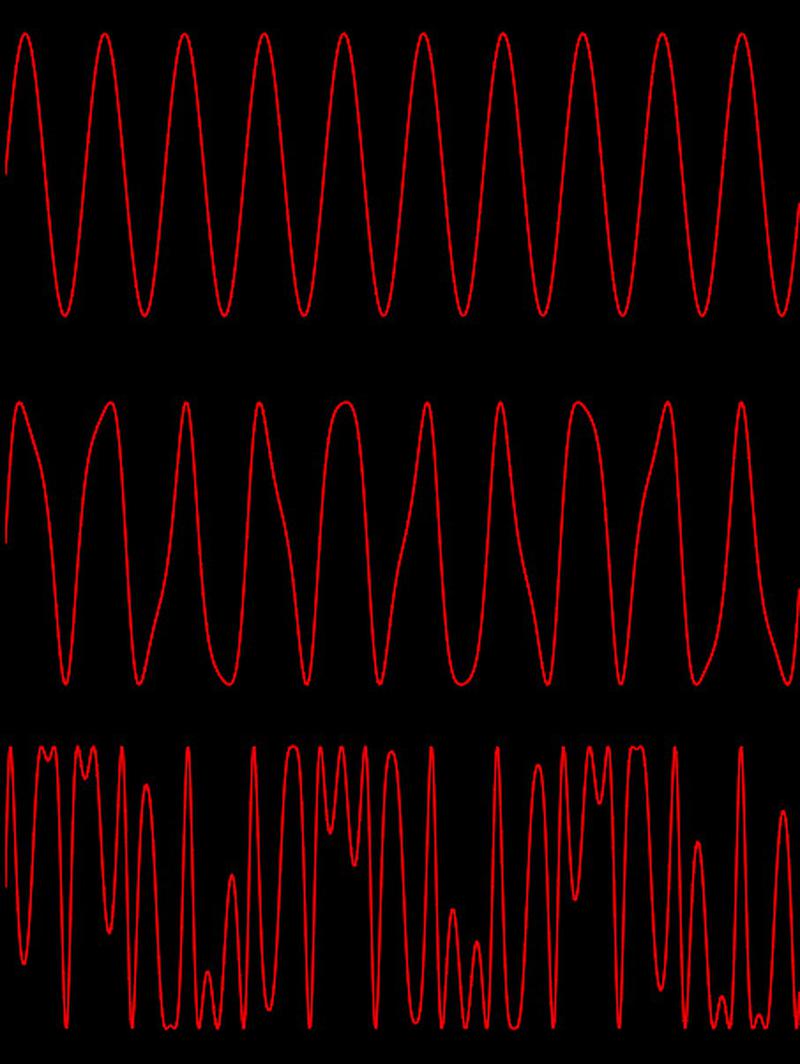
Modulation examples. The top sine wave is unmodulated. The middle wave has a small amount of modulation. The bottom wave is highly modulated.
Algorithms
The above section illustrated how two oscillators can be combined with modulation.
The DX7 extends this principle,
generating a note by combining six oscillators through modulation and summing.
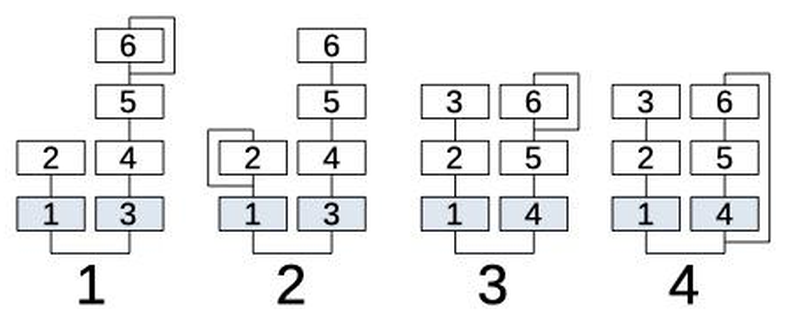
It implements 32 different ways of combining these oscillators, illustrated below, and calls each one an algorithm.
The different algorithms provide flexibility and variety in sound creation.
Multiple levels of modulation create harmonically-rich sounds. On the other hand, multiple output operators allow different sounds to be combined.
An electric piano sound, for example, could have one sound for the hammer thud, a second sound for the body of the tone, and a third sound for the ringing tine,
all varying over time.
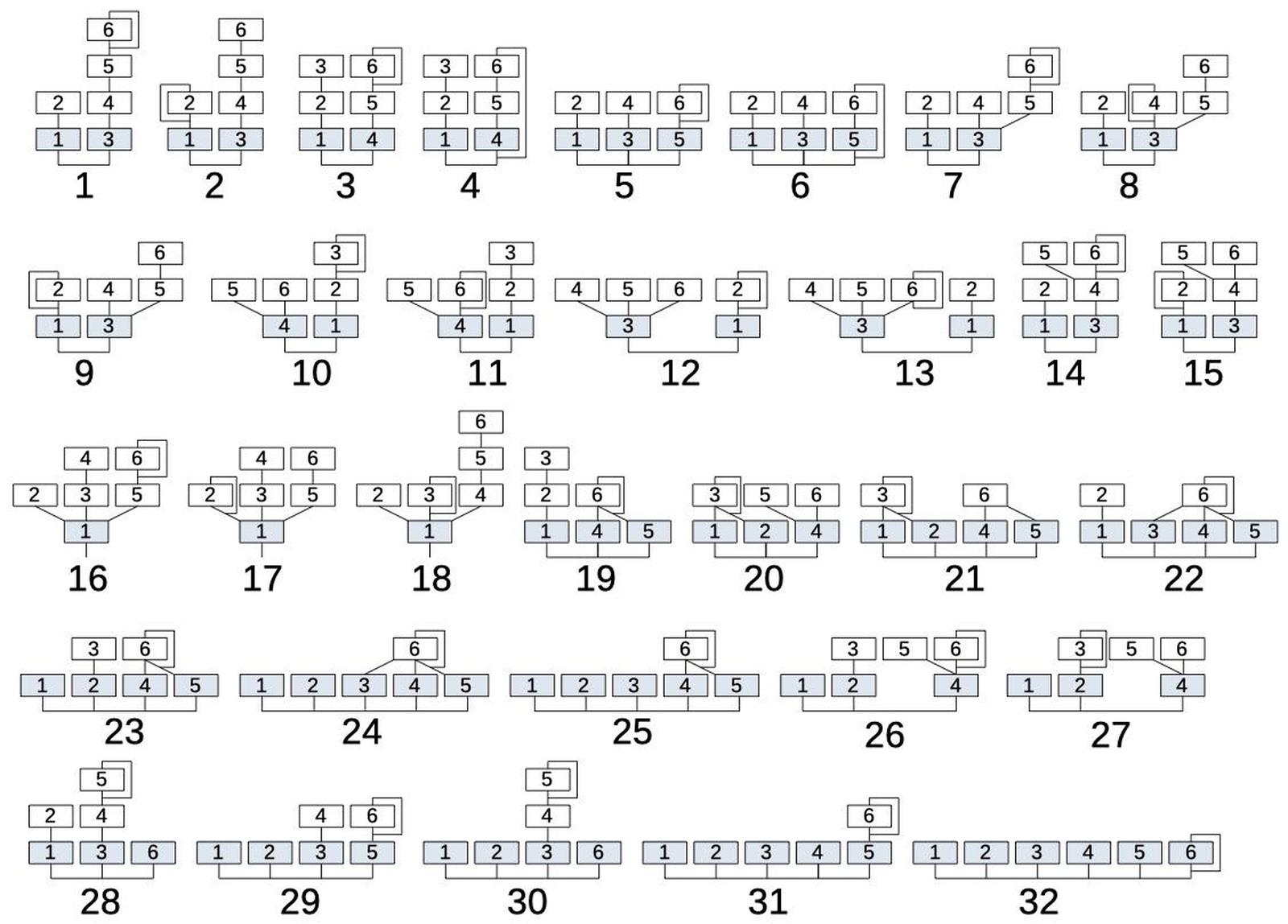
The 32 algorithms of the DX7 synthesizer.
Looking at algorithm #8, for example, shows the structure of an algorithm.
Each box represents an operator (oscillator).
Operators 1 and 3 (in blue), are combined to form the output.
The remaining operators provide modulation, as indicated by the lines.
Operator 2 modulates operator 1.
Operators 4 and 5 are combined to modulate operator 3, providing a complex modulation.
Operator 6, in turn, modulates operator 5.
Finally, the line looping around operator 4 indicates that operator 4 modulates itself.
Since each modulation level can vary over time, the resulting sound can be very complex.
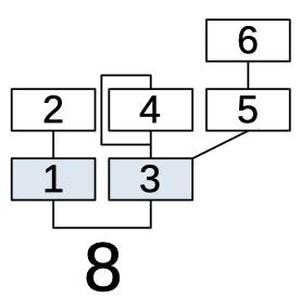
Algorithm 8 combines the six operators; two produce outputs.
Shift-register storage
To understand the DX7's architecture, it's important to know that
the chip uses shift registers, rather than RAM, for its storage.
The idea is that bits are shifted from stage to stage each clock cycle. When a bit reaches the end of the shift register, it can be fed back into the register or
a new bit can be inserted.
For the phase accumulators, the shift registers are 96 bits long since there are 96 oscillators.
Other circuits use 16 bit-shift registers to hold values for the 16 voices.
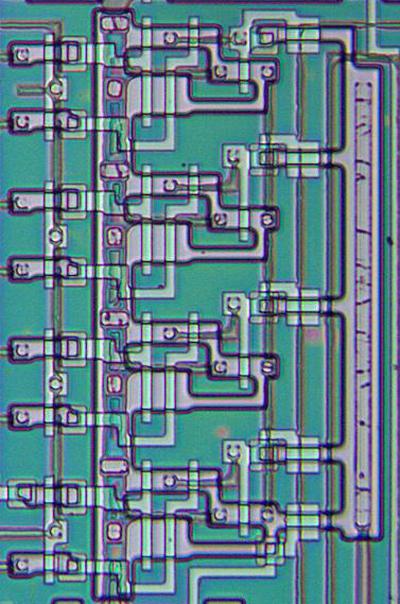
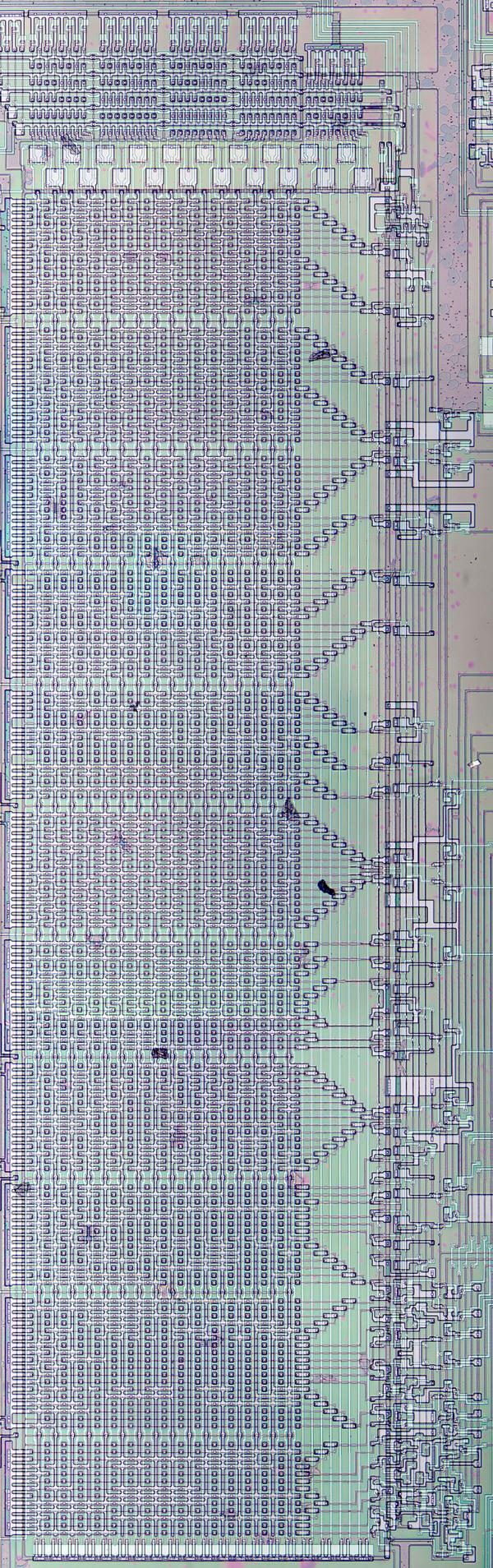
The shift register circuitry (below) is dense, but even so, it takes up a large fraction of the chip.

A small part of the shift register storage.
The use of shift registers greatly affects the design of the DX7 chip.
In particular, values cannot be accessed arbitrarily, as in RAM.
Instead, values can only be used when they exit the shift register, which makes the circuit design much more constrained.
Moreover, circuits must be carefully designed so that each path of a computation takes the same number of cycles (e.g. 16 cycles).
Shorter paths must be delayed as necessary.2
I want to emphasize how unusual this chip is, compared to a microprocessor.
You might expect that an algorithm is implemented with code, for example reading operator 2, applying modulation to operator 1, and then storing the result in operator 1.
Instead, computation happens continuously in the chip, with data moving into the circuitry every clock cycle as it comes from the shift registers.
The chip is more like an assembly line with bits constantly moving on many conveyor belts, and circuits steadily operating on bits as they move by.
An advantage of this approach is that every clock cycle, calculations happen in parallel in multiple parts of the chip, providing much higher performance than a microprocessor could in the 1980s.
Implementation of the algorithms
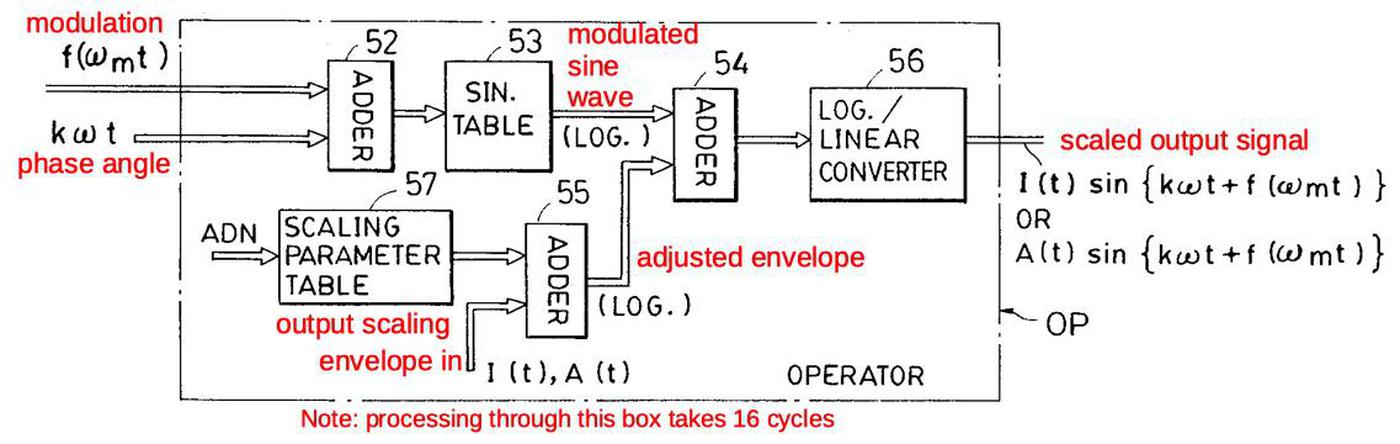
The block diagram below shows the overall structure of the OPS sound chip.
The idea is that the envelope chip (EGS) constantly provides frequency (F) and envelope control (EC) values at the top.
The DX7's control CPU updates the algorithm (A) if the user selects a new one.
The sound chip generates digital data (DA) for the 16 voices, which is fed out at the right. (The DX7's digital-to-analog converter circuitry (DAC) converts these digital
values to the analog sound from the synthesizer.)
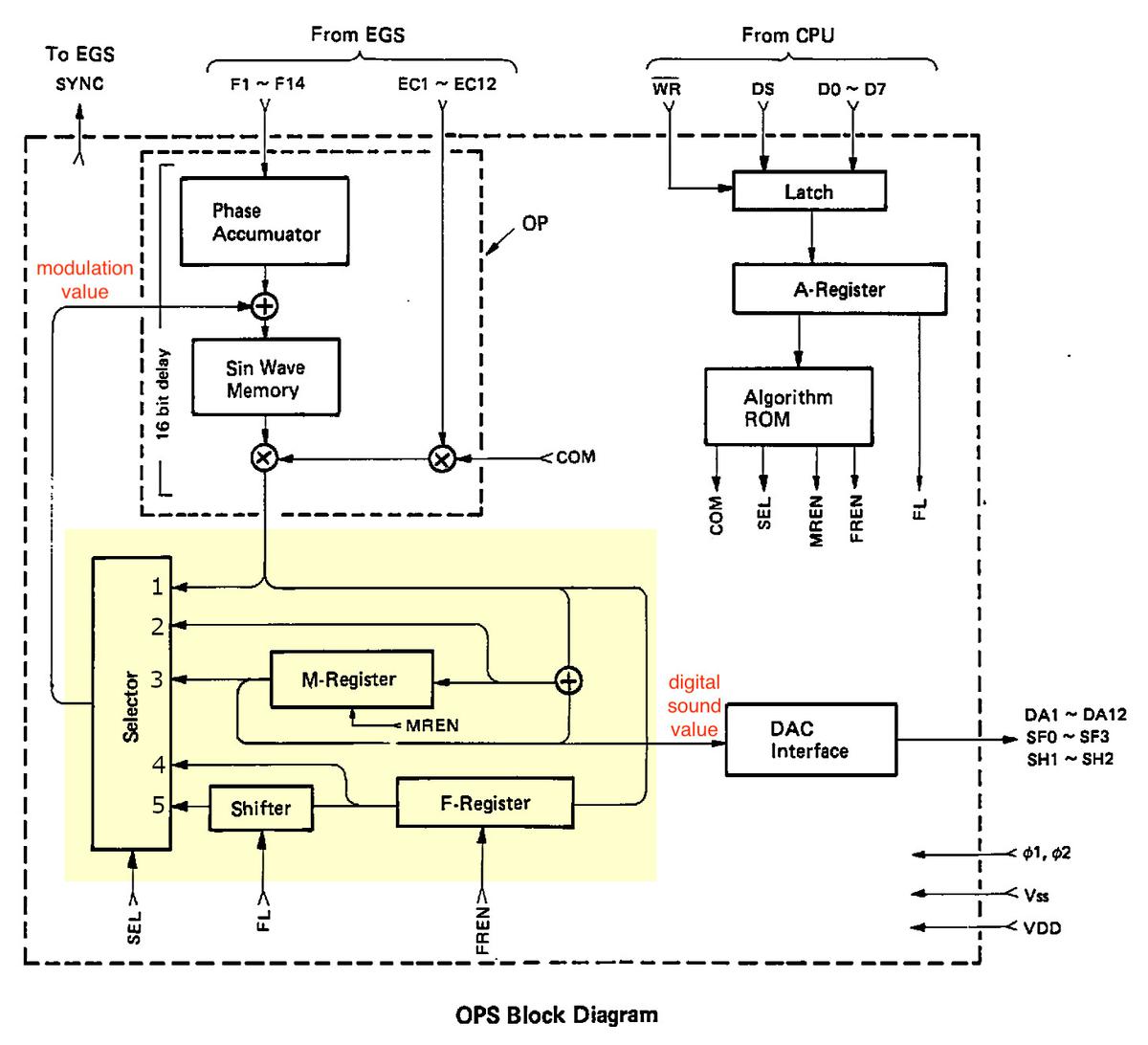
In more detail, the circuitry in the upper left generates the phase values for the 96 oscillators and looks up the values in the sine wave table.
In the lower-left, the highlighted block implements the algorithm, producing two outputs.
This block contains its own storage: the memory (M) register and feedback (F) register.
It generates a modulation value that modulates the index into the sine wave table.
It also produces the digital sound value that is the output from the chip.
(This highlighted block is the focus of this article.)
At the right, the CPU specifies the algorithm number; the algorithm ROM specifies the algorithm by generating control signals COM, SEL, and so forth.
The DX7 has 96 oscillators, which are updated in sequence.
The cycle of 96 updates takes place as shown below.
In the first clock cycle, computation starts for operator 6 of voice (channel) 1.
In the next clock cycles, operator 6 processing starts for voices 2 through 16.
Next, operator 5 is processed for the 16 voices, and likewise for operators 4 to 1.
At the end of this cycle, all the notes have been updated.
Two factors are important here.
First, operators are processed "backward", starting at 6 and ending at 1.
Second, for a particular voice, there are 16 clock cycles between successive operators.
This means that 16 cycles are available to compute each operator.
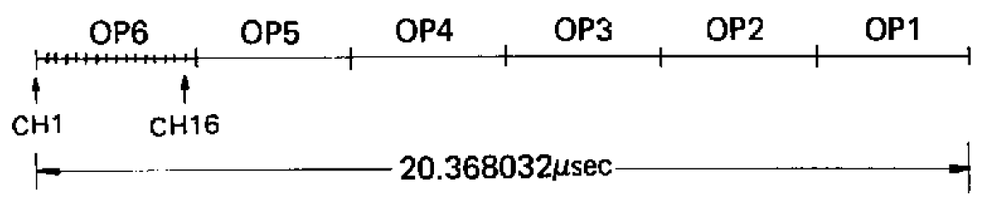
A complete processing cycle, as shown in the service manual. The overall update rate is 49.096 kHz providing reasonable coverage of the audio spectrum.
The diagram below provides more detail of highlighted block above, the circuitry that modulates the waveform according to a particular algorithm.
The effect of modulation is to perturb the phase angle before lookup in the sine wave table.3
At the bottom right, the signal from operator N+1 enters, and is used to compute the modulation for operator N, exiting at the bottom left.
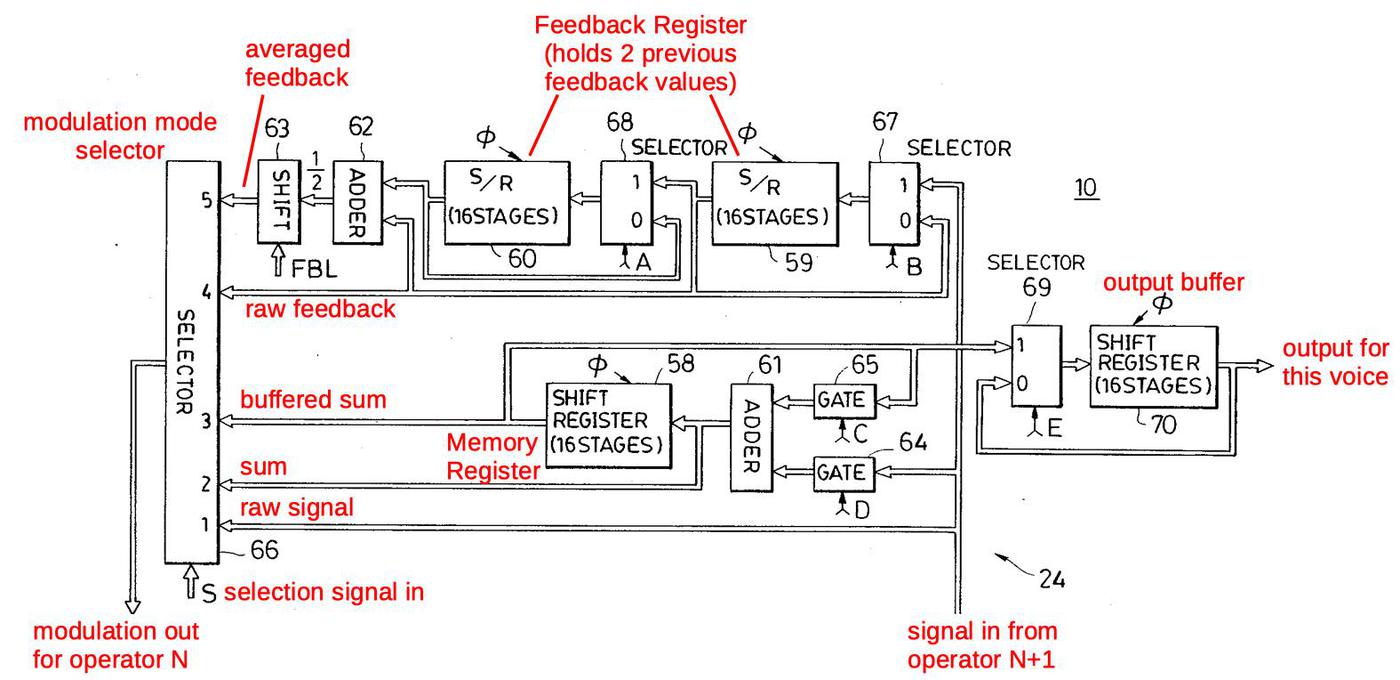
Diagram showing modulation computation, from
the patent. Inconveniently, the signal names are inconsistent with the service manual.
The key component is the selector at the left, which selects one of the five modulation choices, based on the control signal S or SEL.
Starting at the bottom of the selector, SEL=1 selects the unmodified signal from the input operator; this implements the straightforward modulation of an operator by another.
Next, SEL=2 uses the value from the adder (61) for modulation. This allows an operator to be modulated by the sum of operators, for instance in algorithm 7.
SEL=3 uses the delayed value from the buffer; this is used solely for algorithm 21, where operator 6 modulates operator 4.
SEL=4 and SEL=5 use the self-feedback operator for modulation. Because the feedback value is buffered in the circuitry, it is available at any time, unlike other operators.
SEL=4 is used to obtain delayed feedback, for instance when operator 6 modulates operator 4 in algorithm 19.
(In most cases, feedback is applied immediately, for instance when operator 6 modulates operator 5, and this uses SEL=1.)
SEL=5 handles the self-feedback case; the previous two feedback values are averaged to provide stability.4
The SEL=0 case is not shown; it causes no modulation to be selected so the operator is unmodulated.
Several control signals (A, B, C, D, E) also control the circuit.
(Confusingly, the patent diagram below uses the names A and B for the feedback register enable (FREN) line.
The memory register enable (MREN) lines are called C and D.)
Signals A and B have the same value: they select if the feedback buffer continues to hold the previous value or loads a new value.
Signals C and D control the buffer/sum shift register.
If C is 1 and D is 0, the register holds its previous value. If C is 0 and D is 1, the input signal is loaded into the register.
If both C and D are 1, the input signal is added to the previous value.
This register can be used to sum two modulation signals, as in algorithm 7. But it is also used to hold and sum the output signals.
(As a consequence, an algorithm can't sum modulation signals and outputs at the same time.)
Signal E loads the algorithm's final output value into the output buffer (70). Signal E and buffer 70 are implemented separately, so I won't discuss them further.
The algorithm ROM
The algorithms are defined by a ROM with 9-bit entries that hold the selector value (SEL), the control signals MREN and FREN (A,C,D), and the compensation scaling value COM (which I explain later).
Each algorithm needs 6 entries in the ROM to select the action for the 6 operators.
Thus, the ROM holds 96 9-bit values.
The photo below shows the algorithm ROM. It has 32 columns, one for each algorithm and 9 groups of 6 rows: one group for each output bit.
From bottom to top, the outputs are three bits for the selector value SEL, two MREN lines and the FREN line, and three bits for the COM value.
The groups of 6 diagonal transistors at the left of the ROM select the entry for the current operator.

The algorithm ROM. The metal layer has been removed to show the silicon structure underneath that defines the bits.
The bits are visible in the pattern of the ROM. By examining the ROM closely, I extracted the ROM data. Each entry is formatted as "SEL / A,C,D / COM". (I only show three entries below; the full ROM is in the footnotes.5)
| | Operator |
|---|
| Algorithm | 6 | 5 | 4 | 3 | 2 | 1 |
|---|
| 1 | 1/100/0 | 1/000/0 | 1/000/1 | 0/001/0 | 1/010/1 | 5/011/0 |
| 2 | 1/000/0 | 1/000/0 | 1/000/1 | 5/001/0 | 1/110/1 | 0/011/0 |
| ... |
| 8 | 1/000/0 | 5/001/0 | 2/111/1 | 0/001/0 | 1/010/1 | 0/011/0 |
To see how an algorithm is implemented, consider operator 8, for instance.6
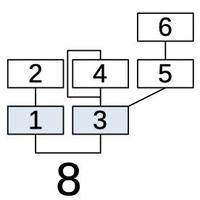
Algorithm 8 has four modulators and two carriers.
Processing of an algorithm starts with
operator 6's signal value at the output of the operator block and operator 5's modulation is being computed.
Table column 6 above shows SEL=1, A,C,D=000.
In the modulation circuit (below), SEL=1 selects the raw signal in (i.e. operator 6's value) for modulation.
Thus, operator 6 modulates operator 5, the desired behavior for algorithm 8.
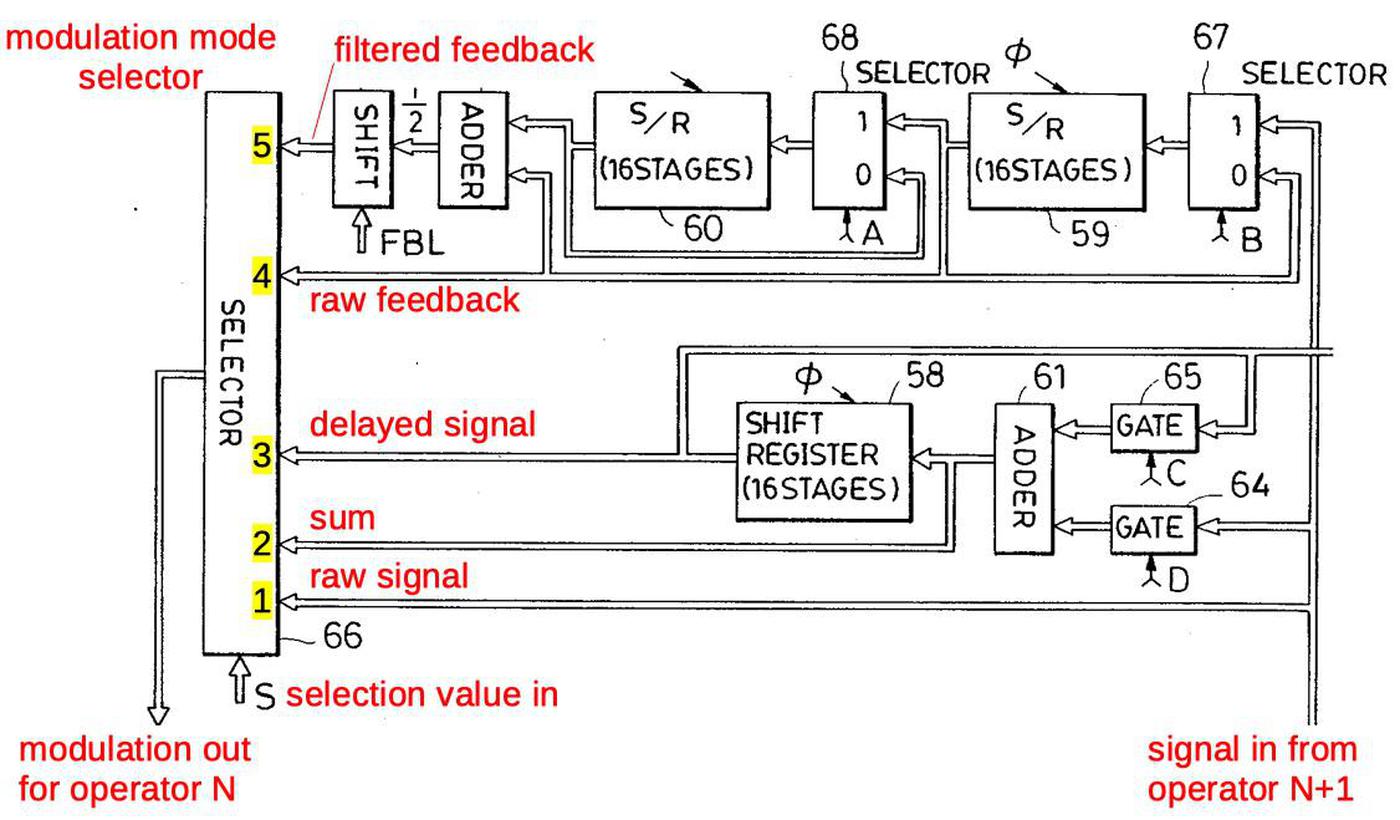
Diagram showing modulation computation.
Next, (16 cycles later), operator 5's signal is at the output and operator 4's modulation is being computed.
Column 5 of the table shows SEL=5, A,C,D=001.
SEL=5 selects the filtered feedback register for self-modulation of operator 4.
D=1 causes operator 5's value to be loaded into the shift register, in preparation for modulating operator 3.
Next, operator 4's signal is at the output and operator 3's modulation is being computed.
Column 4 shows SEL=2 and A,C,D=111.
Bits A (and B) are 1 to load the feedback register with operator 4's value, updating the self-feedback for operator 4.
Bits C and D cause operator 4 to be added to the previously-stored operator 5 value.
SEL=2 selects this sum for operator 3's modulation, so operator 3 is modulated by both operators 4 and 5.
COM=1 indicates this operator is one of 2 outputs, so operator 3's value will be divided by 2 as it is computed.
Next, operator 3's signal is at the output and operator 2's modulation is being computed.
Looking at the ROM, SEL=0 results in no modulation of operator 2.
D=1 loads operator 3's signal into the summing shift register, in preparation for the output.
Next, operator 2's signal is at the output and operator 1's modulation is being computed.
SEL=1 causes operator 1 to be modulated by operator 2.
C=1 so the summing shift register continues to hold the operator 3 value, to produce the output.
As with operator 3, COM=1 so operator 1's value will be divided by 2 when it is computed.
Finally, operator 1's signal is at the output and operator 6's modulation is being computed.
SEL=0 indicates no modulation of operator 6.
Control signals C and D are 1 so operator 1 is added to the register (which holds operator 3's value), forming the final output.
This process repeats cyclically, interleaved with processing for the 15 other voices.
This section illustrates how a complex algorithm is implemented through the modulator circuitry, directed by a few control signals from the ROM.
The other algorithms are implemented in similar ways.7
The modulation circuitry
The diagram below shows the circuitry that computes the modulation and output; this functional block is in the center of the chip.
The memory register (red) holds 16 values, one for each voice. To its right, the adder (blue) adds to the value in the memory register.
The selector (purple), is the heart of the circuit, selecting which value is used for modulation.
It is controlled by the selector decoder (orange) at the bottom, which activates a control line based on the 3-bit SEL value.
At the far right, the two feedback registers (red) hold the last two feedback values for each of the 16 voices.
The feedback adder sums two feedback values to obtain the average.
The feedback shifter (yellow) scales the feedback value by a power of 2.
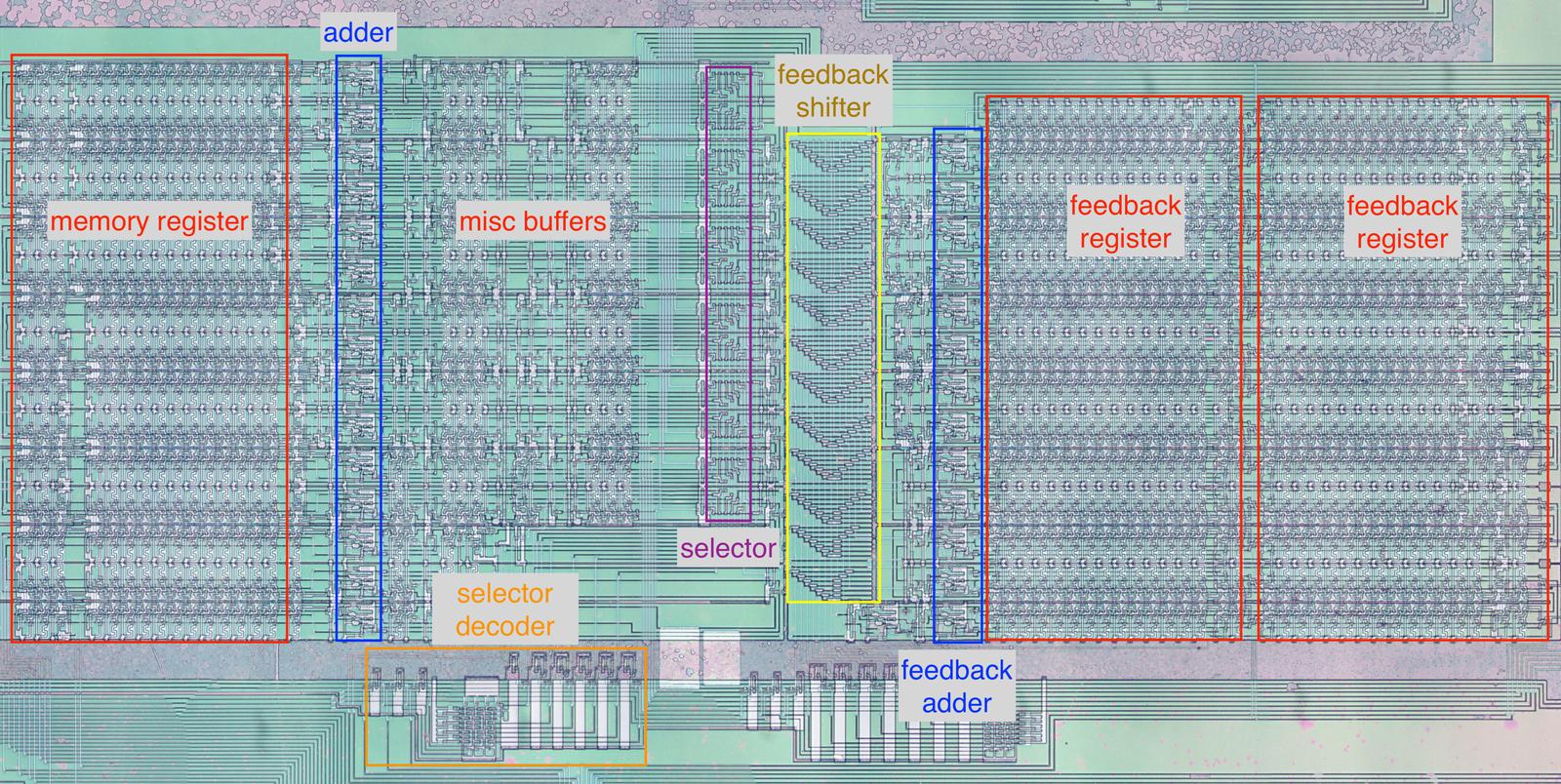
The circuitry that calculates the modulation for the algorithm.
Shift registers
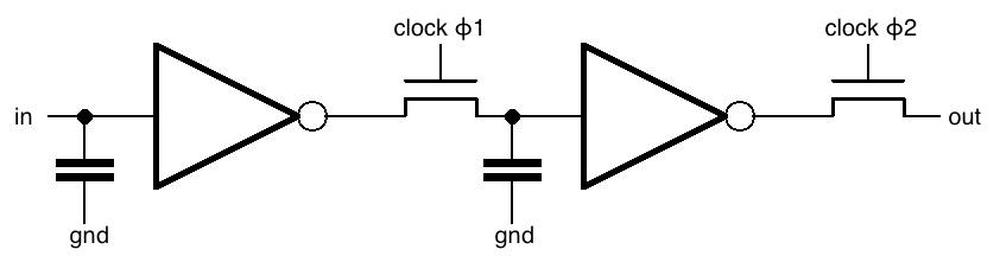
The schematic below shows how one stage of the shift register is implemented.
The chip uses a two-phase clock.
In the first phase, clock ϕ1 goes high, turning on the first transistor.
The input signal goes through the inverter, through the transistor, and the voltage is stored in the capacitor.
In the second phase, clock ϕ2 goes high, turning on the second transistor.
The value stored in the capacitor goes through the second inverter, through the second transistor, and to the output, where it enters the next shift register stage.
Thus, in one clock cycle (ϕ1 and then ϕ2), the input bit is transferred to the output.
(The circuit is similar to dynamic RAM in the sense that bits are stored in capacitors.
The clock needs to cycle before the charge on the capacitor drains away and data is lost.
The inverters amplify and regenerate the bit at each stage.)
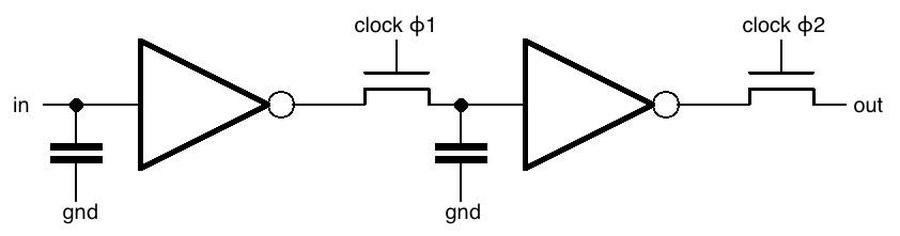
Schematic of one stage of the shift register.
The diagram below shows part of the shift register circuitry as it appears on the die.
The blue rectangle indicates one shift register stage.
The power, ground, and clock wiring is in the metal layer, which was mostly removed in this image.
Shift register stages are linked horizontally.
Shift registers for separate bits are stacked vertically, with alternating rows mirrored.
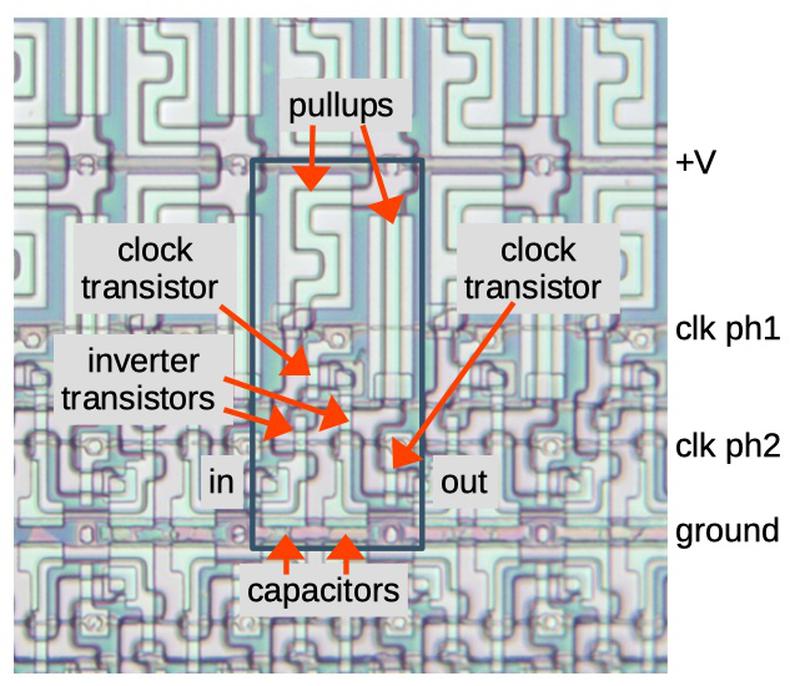
Die photo showing a stage of the shift register.
The selector
The selector circuit selects one of the five potential multiplexer values, based on the SEL input.
The circuit uses five pass transistors (indicated in yellow) that pass one of the 5 inputs to the driver circuit and then the output.
(A sixth transistor pulls the output high if none of the inputs is selected; I've labeled this "x".)
The diagram below shows one selector in the top half, and a mirror-image selector below; there are 12 selector circuits in total.
The circuit is built around the six vertical select lines.
One select line is activated to select a particular value. This turns on the corresponding transistors, allowing that input to flow through the transistors.
The result goes through another transistor to synchronize it to the clock, and then an inverter/buffer to drive the output line.
The outputs go to the sine-wave circuit, where they modulate the input to the lookup table.
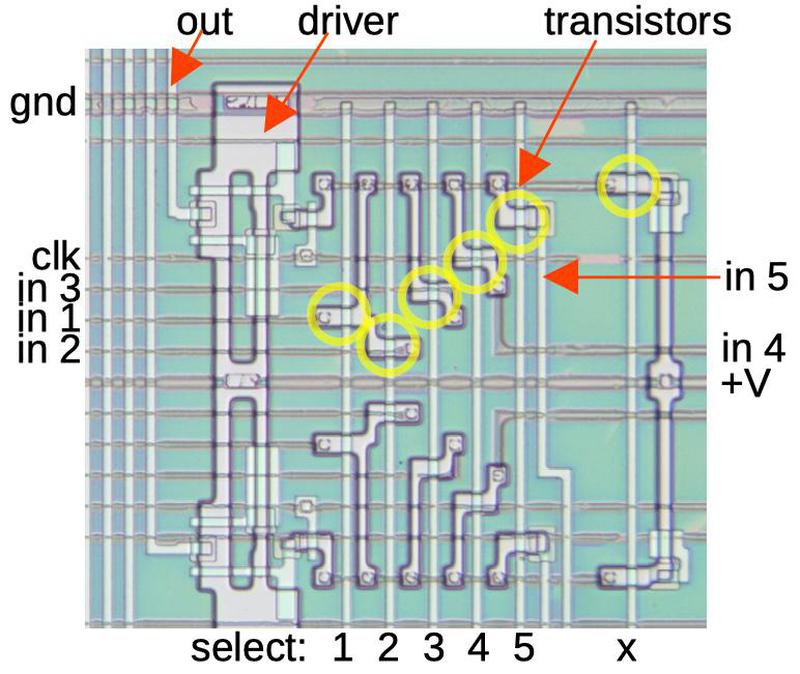
Two stages of the selector.
The adder
The chip contains multiple adders. Two adders are used in the modulation computation: one to sum operators and one to average the two previous feedback values.
The adders are implemented with a standard binary circuit called a full adder.
A full adder takes two input bits and a carry-in bit. It adds these bits to generate a sum bit and a carry-out bit.
By combining full adders, larger binary numbers can be added.
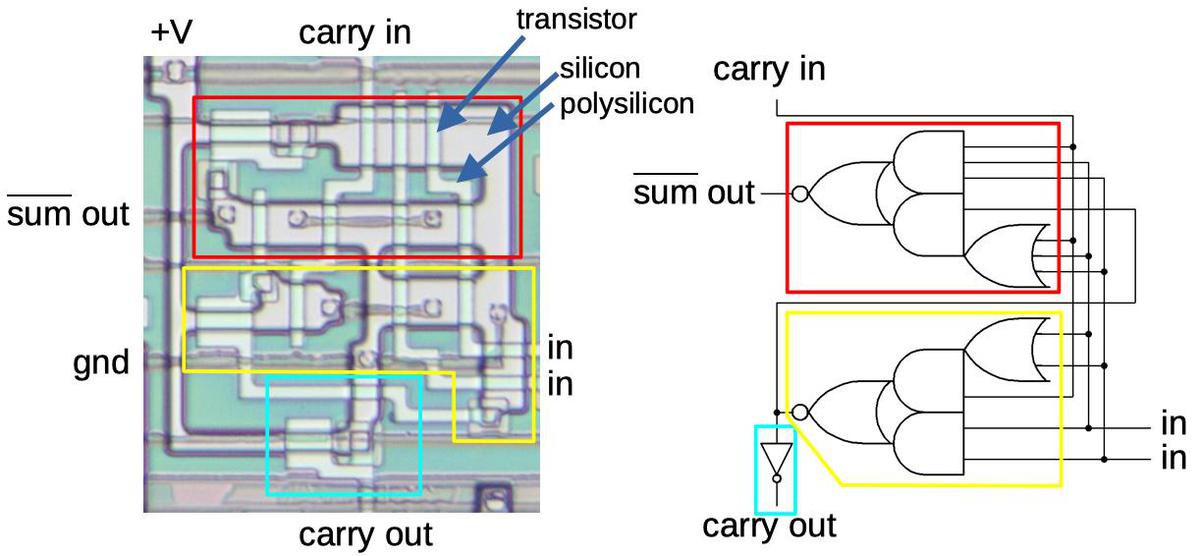
Diagram showing a full adder.
The diagram above shows a full adder stage in the chip. The circuit is built from three relatively complex gates, but if you try the various input combinations, you
can see that produces the sum and carry.
(Due to the properties of NMOS circuits, it's more efficient to use a small number of complex gates rather than a larger number of simple gates such as NAND gates.)
One problem with binary addition is that it can be relatively slow for carries to propagate through all the stages. (This is the binary equivalent of 99999 + 1.)
The solution used in the DX7 is pipelining: an addition operation is split across multiple clock cycles, rather than being completed in a single clock cycle.
This reduces the number of carries in one clock cycle.
Although a particular addition takes several clock cycles, the adders are kept busy with other additions, so one addition is completed every cycle.
The compensation (COM) computation
In the DX7, different algorithms have different numbers of oscillators in the output, which poses a problem
An algorithm with 6 output oscillators (e.g. #32) would be six times as loud as an algorithm with 1 oscillator (e.g. #16), which would be annoying as the user changes the algorithm.
To avoid this problem, the chip scales the level of output oscillators accordingly. For instance, the levels of output oscillators in algorithm #32
are scaled by 1/6 to even out the volumes.
This factor is called COM (compensation) in the service manual and ADN (addition channel number) in the patent.8
To implement this scaling, the algorithm ROM holds the output count for each operator, minus 1.
For example, algorithm #32 has six output oscillators, each one having a COM value of 5 (i.e. 6-1).
For algorithm #1, the two output oscillators are 1 and 3: these have a COM value of 1 (i.e. 2-1).
Operators that are used for modulation are not scaled, and have a COM value of 0.
Recall that the envelope scaling is accomplished by adding base-2 logarithms. The COM scaling also uses logarithms, which are subtracted to scale down the output level.
A small ROM generates 6-bit logarithms for the COM values 1 through 5, corresponding to scale factors 2 through 6.
The diagram below shows the COM circuitry, which is in the upper-right corner of the chip.
At the left, the decoder and tiny ROM determine the logarithmic scaling factor from the number of inputs.
This is added to the logarithmic envelope level that the chip receives from the envelope chip.
The result goes through a few shift register stages for timing reasons.
The COM circuitry adds a compensation level to the envelope to compensate for algorithms with multiple outputs.
Conclusion
The DX7's algorithm implementation circuitry is at the heart of the chip's sound generation.
This circuitry is cleverly designed to implement 32 different algorithms at high speed with the limited hardware of the 1980s.
The circuitry runs fast enough to process 16 voices sequentially, each with 6 separate oscillators, while producing outputs fast enough to produce audio signals.
By taking advantage of the pipelined architecture built around shift registers, the chip processes a different oscillator during each clock cycle, a remarkable throughput.
Overall, I'm impressed with the design of this chip.
Its cutting-edge design was the key to the DX7's ability to provide dramatic new sounds at a low price.
As a result, the DX7 defined the canonical sound of the 1980s and changed the direction of pop music.
I plan to continue investigating the DX7's circuitry,
so follow me on Twitter @kenshirriff for updates. I also have an RSS feed.
Also see my previous posts on the DX7:
DX7 reverse-engineering,
the exponential ROM,
The log-sine ROM.
Thanks to Jacques Mattheij and Anthony Richardson for providing the chip and discussion.9
Notes and references