What happens if you give the Intel 8086 processor an instruction that doesn't exist? A modern microprocessor (80186 and later) will generate an exception, indicating that an illegal instruction was executed. However, early microprocessors didn't include the circuitry to detect illegal instructions, since the chips didn't have transistors to spare. Instead these processors would do something, but the results weren't specified.1
The 8086 has a number of undocumented instructions. Most of them are simply duplicates of regular instructions, but a few have unexpected behavior, such as revealing the values of internal, hidden registers. In the 8086, most instructions are implemented in microcode, so examining the 8086's microcode can explain why these instructions behave the way they do.
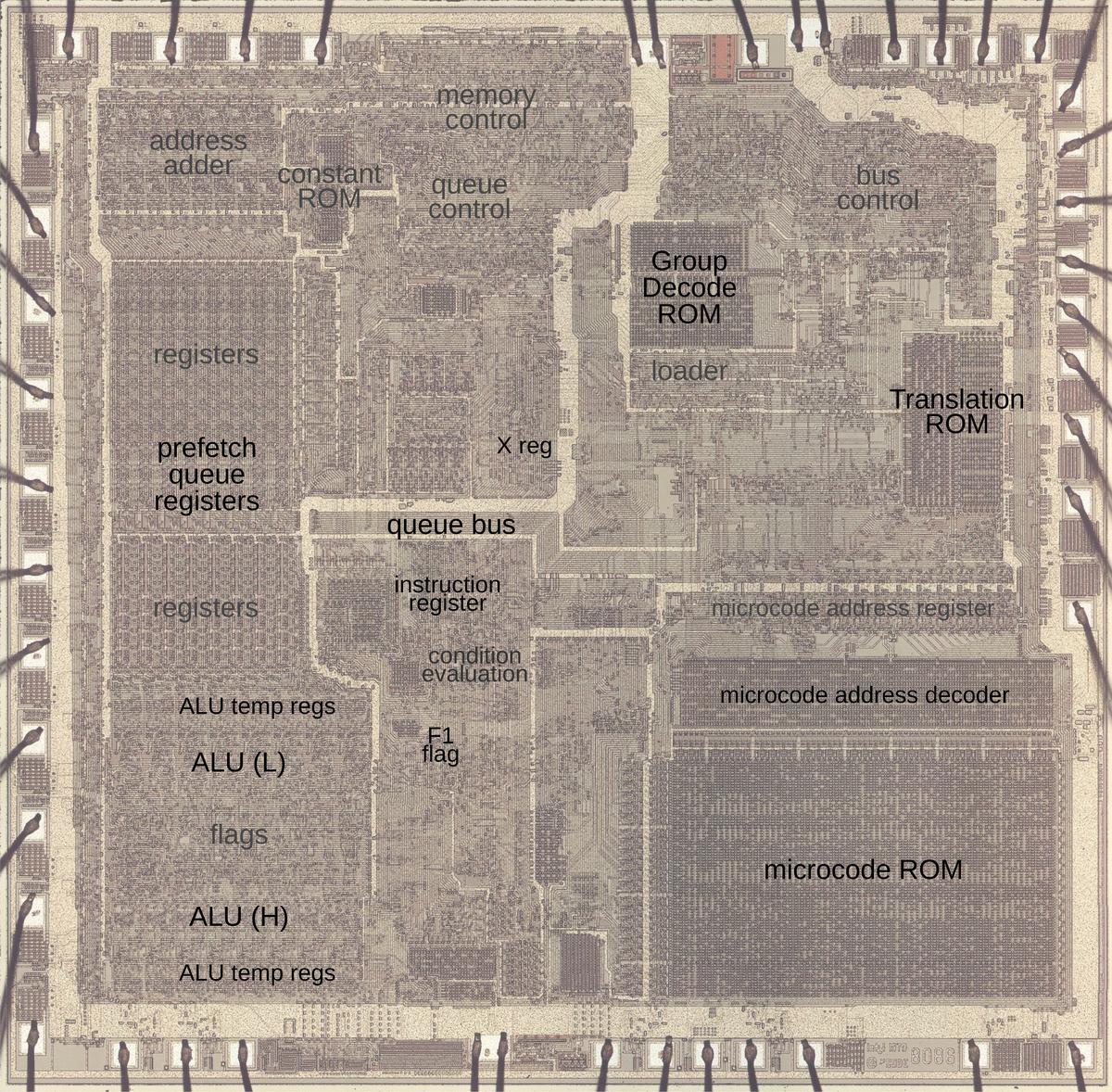
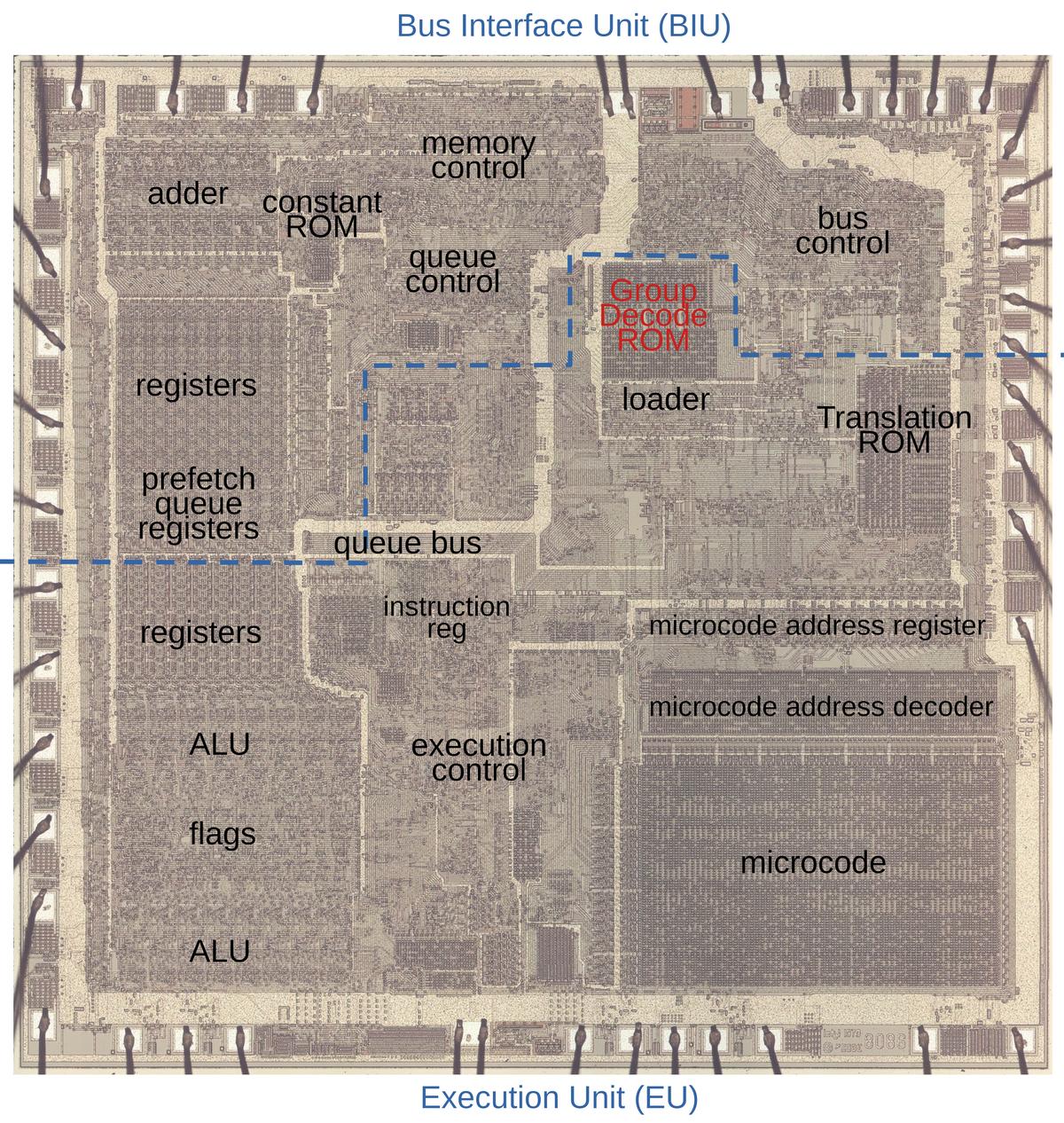
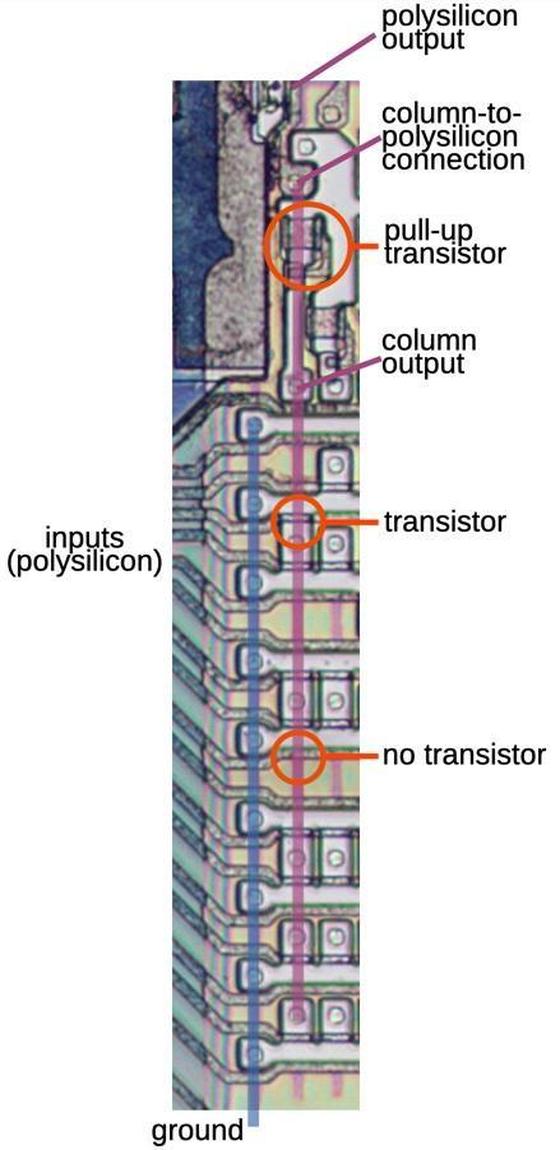
The photo below shows the 8086 die under a microscope, with the important functional blocks labeled. The metal layer is visible, while the underlying silicon and polysilicon wiring is mostly hidden. The microcode ROM and the microcode address decoder are in the lower right. The Group Decode ROM (upper center) is also important, as it performs the first step of instruction decoding.
Microcode and 8086 instruction decoding
You might think that machine instructions are the basic steps that a computer performs. However, instructions usually require multiple steps inside the processor. One way of expressing these multiple steps is through microcode, a technique dating back to 1951. To execute a machine instruction, the computer internally executes several simpler micro-instructions, specified by the microcode. In other words, microcode forms another layer between the machine instructions and the hardware. The main advantage of microcode is that it turns the processor's control logic into a programming task instead of a difficult logic design task.
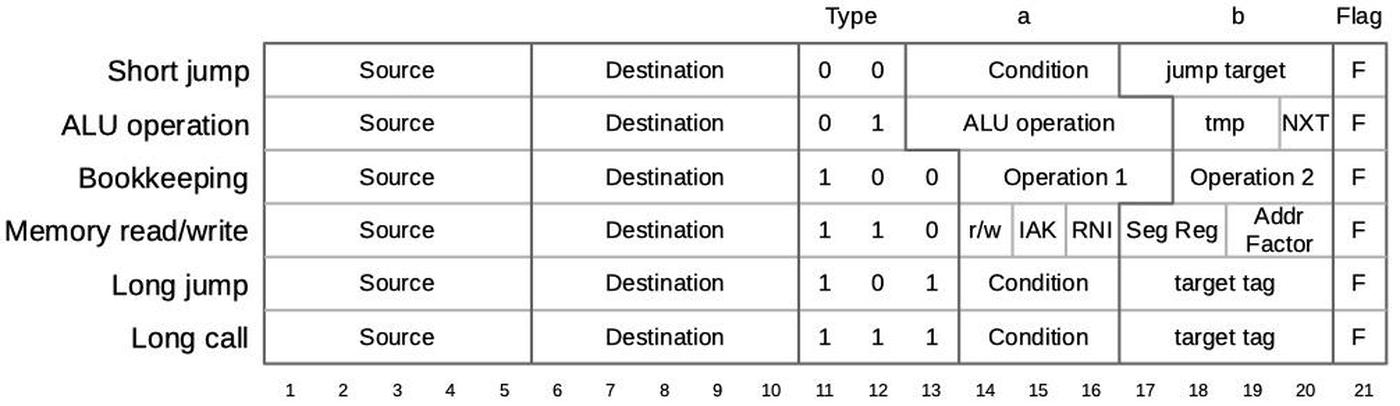
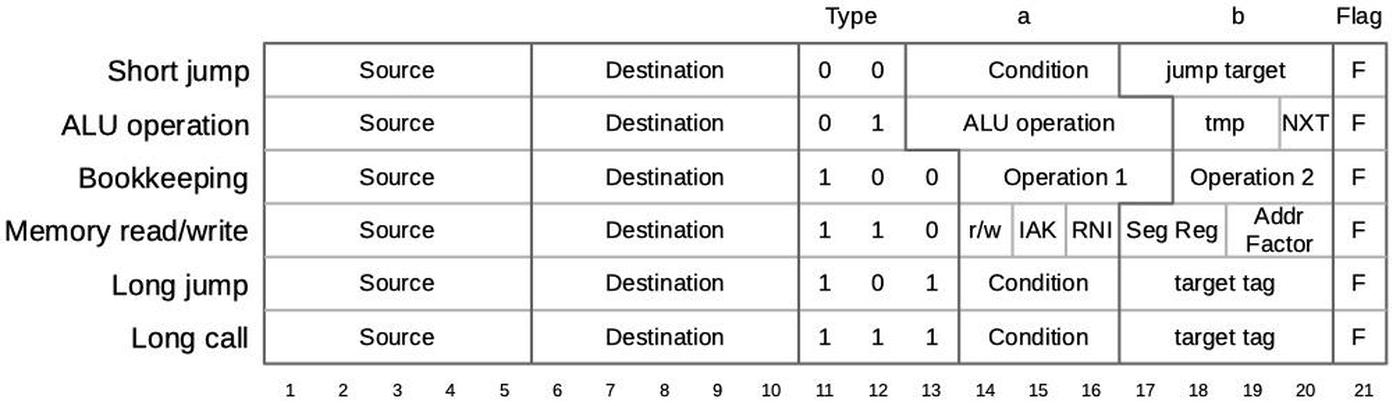
The 8086's microcode ROM holds 512 micro-instructions, each 21 bits wide. Each micro-instruction performs two actions in parallel. First is a move between a source and a destination, typically registers. Second is an operation that can range from an arithmetic (ALU) operation to a memory access. The diagram below shows the structure of a 21-bit micro-instruction, divided into six types.
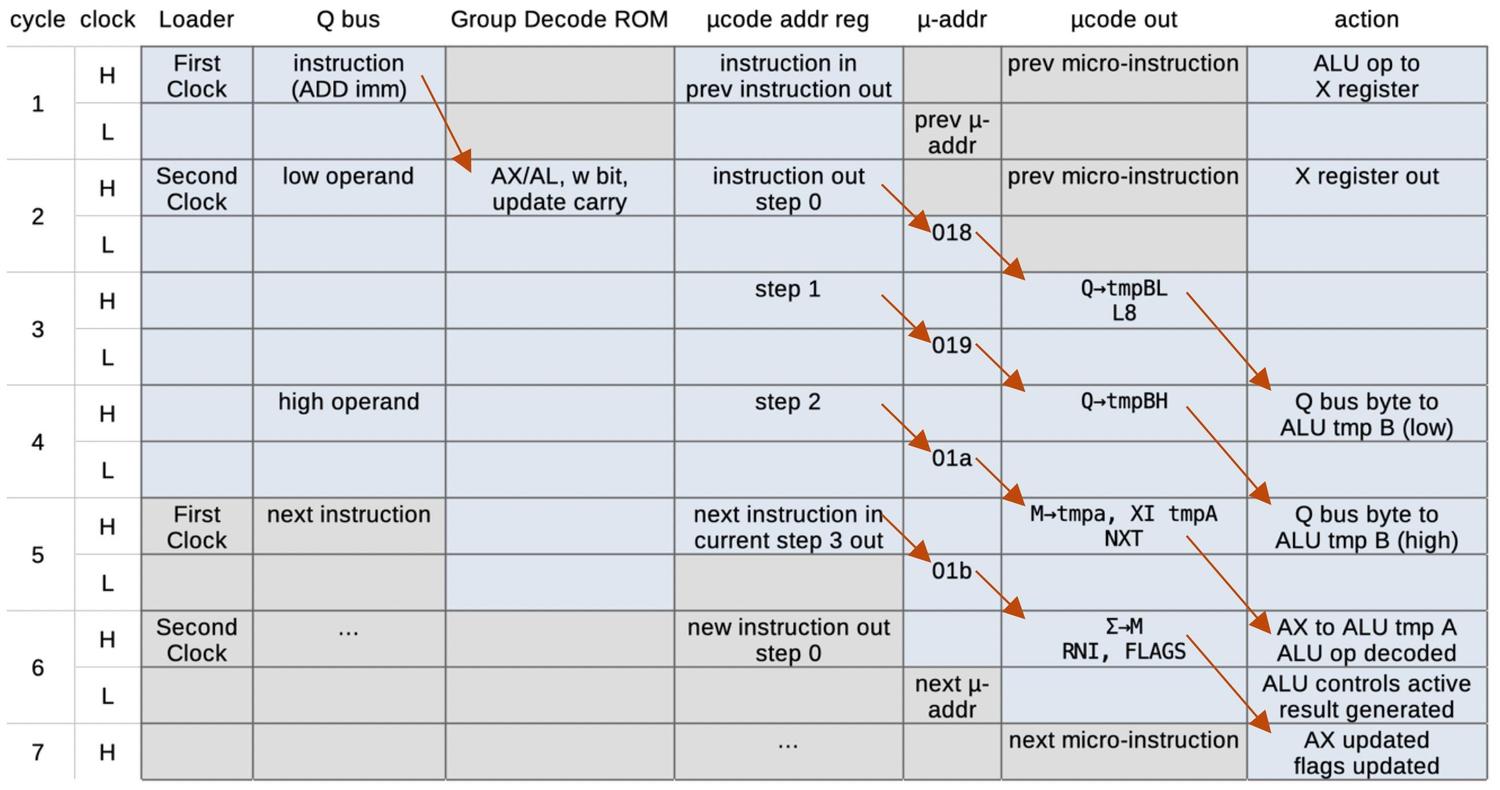
When executing a machine instruction, the 8086 performs a decoding step.
Although the 8086 is a 16-bit processor, its instructions are based on bytes. In most cases, the first byte specifies the
opcode, which may be followed by additional instruction bytes.
In other cases, the byte is a "prefix" byte, which changes the behavior of the following instruction.
The first byte is analyzed
by something called the Group Decode ROM.
This circuit categorizes the first byte of the instruction into about 35 categories that control how the instruction is
decoded and executed.
One category is "1-byte logic"; this indicates a one-byte instruction or prefix that is simple and implemented by logic circuitry in the 8086.
For instructions in this category, microcode is not involved while
the remaining instructions are implemented in microcode.
Many of these instructions are in the "two-byte ROM" category indicating that the instruction has a second byte
that also needs to be decoded by microcode.
This second byte, called the ModR/M byte, specifies that memory addressing mode or registers that the instruction uses.
The next step is the microcode's address decoder circuit, which determines where to start executing microcode based on the opcode. Conceptually, you can think of the microcode as stored in a ROM, indexed by the instruction opcode and a few sequence bits. However, since many instructions can use the same microcode, it would be inefficient to store duplicate copies of these routines. Instead, the microcode address decoder permits multiple instructions to reference the same entries in the ROM. This decoding circuitry is similar to a PLA (Programmable Logic Array) so it matches bit patterns to determine a particular starting point. This turns out to be important for undocumented instructions since undocumented instructions often match the pattern for a "real" instruction, making the undocumented instruction an alias.
The 8086 has several internal registers that are invisible to the programmer but are used by the microcode.
Memory accesses use the Indirect (IND) and Operand (OPR) registers; the IND register holds the address in the segment,
while the OPR register holds the data value that is read or written.
Although these registers are normally not accessible by the programmer, some undocumented instructions provide access to these registers, as will be described later.
The Arithmetic/Logic Unit (ALU) performs arithmetic, logical, and shift operations in the 8086.
The ALU uses three internal registers: tmpA, tmpB, and tmpC. An ALU operation requires two micro-instructions.
The first micro-instruction specifies the operation (such as ADD) and the temporary register that holds one argument (e.g. tmpA);
the second argument is always in tmpB.
A following micro-instruction can access the ALU result through the pseudo-register Σ (sigma).
The ModR/M byte
A fundamental part of the 8086 instruction format is the ModR/M byte, a byte that specifies addressing for many instructions. The 8086 has a variety of addressing modes, so the ModR/M byte is somewhat complicated. Normally it specifies one memory address and one register. The memory address is specified through one of eight addressing modes (below) along with an optional 8- or 16-bit displacement in the instruction. Instead of a memory address, the ModR/M byte can also specify a second register. For a few opcodes, the ModR/M byte selects what instruction to execute rather than a register.
The implementation of the ModR/M byte plays an important role in the behavior of undocumented instructions.
Support for this byte is implemented in both microcode and hardware.
The various memory address modes above are implemented by microcode subroutines, which compute the appropriate memory address and
perform a read if necessary.
The subroutine leaves the memory address in the IND register, and if a read is performed, the value is in the OPR register.
The hardware hides the ModR/M byte's selection of memory versus register, by making the value available through the pseudo-register M, while the second register is available through N.
Thus, the microcode for an instruction doesn't need to know if the value was in memory or a register, or which register was selected.
The Group Decode ROM examines the first byte of the instruction to determine if a ModR/M byte is present, and if a read
is required.
If the ModR/M byte specifies memory, the Translation ROM determines which micro-subroutines to call before handling the
instruction itself.
For more on the ModR/M byte, see my post on Reverse-engineering the ModR/M addressing microcode.
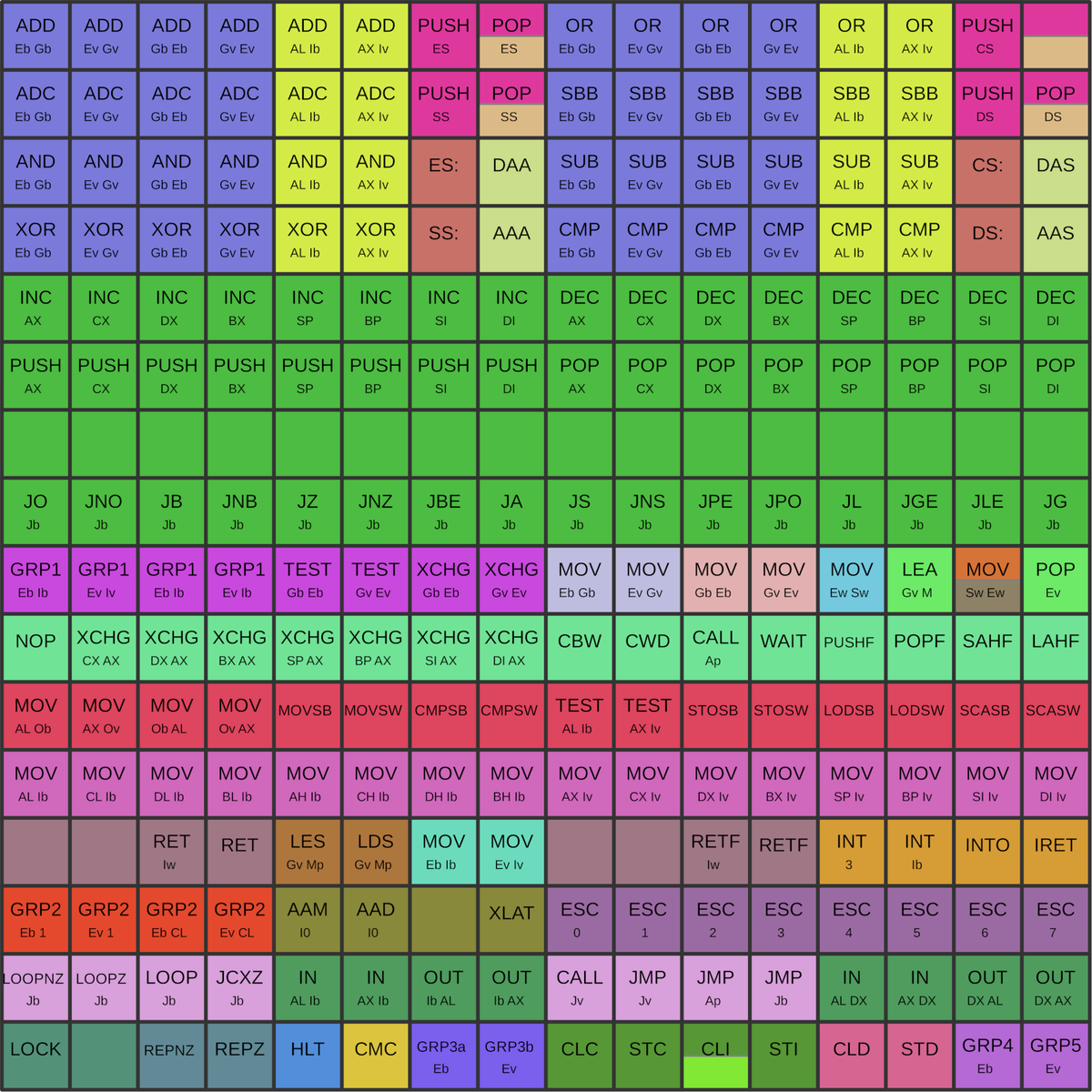
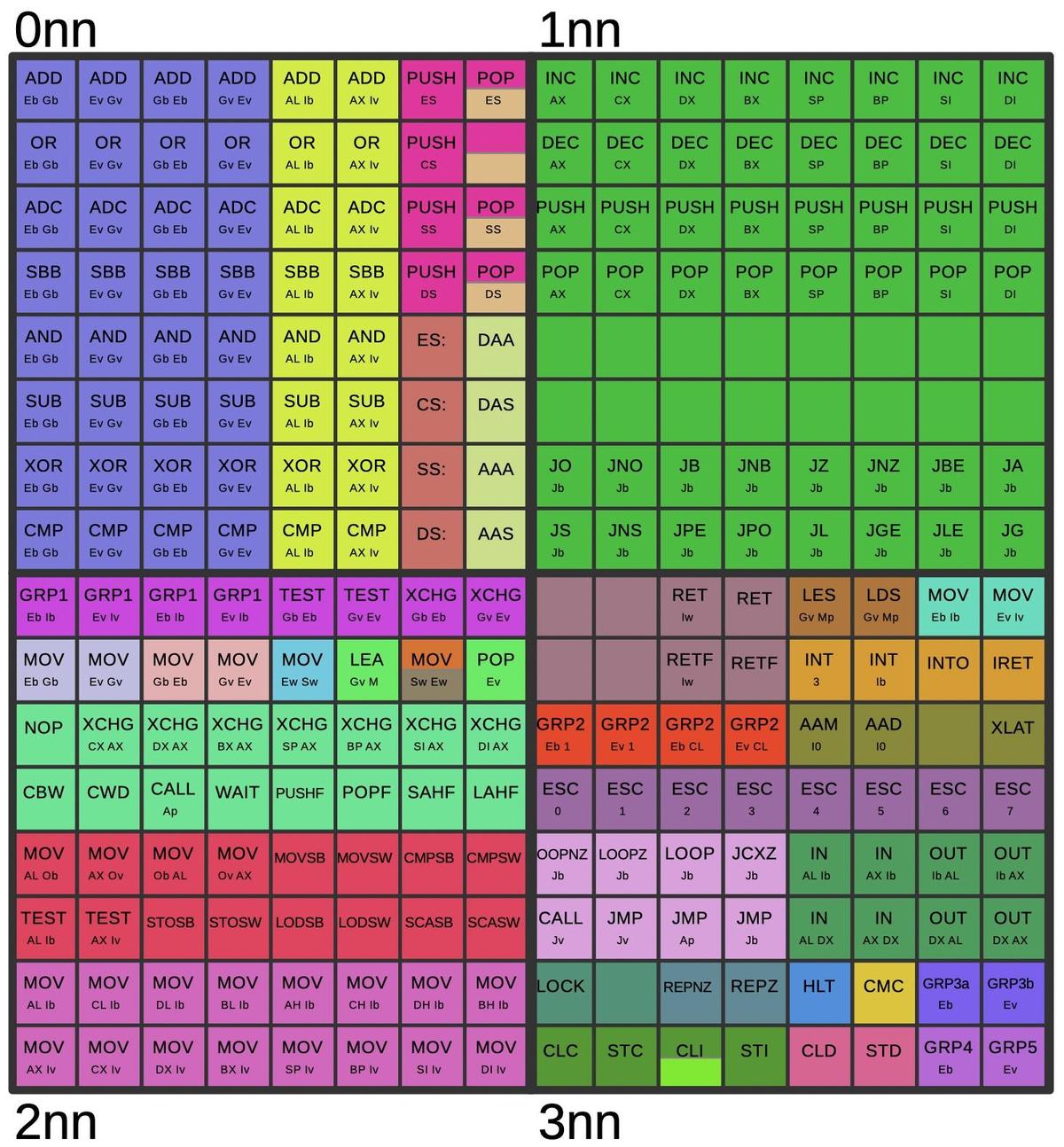
Holes in the opcode table
The first byte of the instruction is a value from 00 to FF in hex.
Almost all of these opcode values correspond to documented 8086 instructions, but there are a few exceptions, "holes" in the opcode table.
The table below shows the 256 first-byte opcodes for the 8086, from hex 00 to FF. Valid opcodes for the 8086 are in white;
the colored opcodes are undefined and interesting to examine.
Orange, yellow, and green opcodes were given meaning in the 80186, 80286, and 80386 respectively.
The purple opcode is unusual: it was implemented in the 8086 and later processors but not documented.2
In this section, I'll examine the microcode for these opcode holes.
D6: SALC
The opcode D6 (purple above) performs a well-known but undocumented operation that is typically called SALC, for Set AL to Carry.
This instruction sets the AL register to 0 if the carry flag is 0, and sets the AL register to FF if the carry flag is 1.
The curious thing about this undocumented instruction is that it exists in all x86 CPUs, but Intel didn't mention it until 2017.
Intel probably put this instruction into the processor deliberately as a copyright trap.
The idea is that if a company created a copy of the 8086 processor and the processor included the SALC instruction, this
would prove that the company had copied Intel's microcode and thus had potentially violated Intel's copyright on the microcode.
This came to light when NEC created improved versions of the 8086, the NEC V20 and V30 microprocessors, and was sued by Intel.
Intel analyzed NEC's microcode but was disappointed to find that NEC's chip did not include the hidden instruction, showing
that NEC hadn't copied the microcode.3
Although a Federal judge ruled in 1989 that NEC hadn't infringed
Intel's copyright, the 5-year trial ruined NEC's market momentum.
The SALC instruction is implemented with three micro-instructions, shown below.4
The first micro-instruction jumps if the carry (CY) is set.
If not, the next instruction moves 0 to the AL register. RNI (Run Next Instruction) ends the microcode execution
causing the next machine instruction to run.
If the carry was set, all-ones (i.e. FF hex) is moved to the AL register and RNI ends the microcode sequence.
JMPS CY 2 SALC: jump on carry
ZERO → AL RNI Move 0 to AL, run next instruction
ONES → AL RNI 2:Move FF to AL, run next instruction
0F: POP CS
The 0F opcode is the first hole in the opcode table.
The 8086 has instructions to push and pop the four segment registers, except opcode 0F is undefined where POP CS should be.
This opcode performs POP CS successfully, so the question is why is it undefined?
The reason is that POP CS is essentially useless and doesn't do what you'd expect, so Intel figured it was best not
to document it.
To understand why POP CS is useless, I need to step back and explain the 8086's segment registers.
The 8086 has a 20-bit address space, but 16-bit registers.
To make this work, the 8086 has the concept of segments: memory is accessed in 64K chunks called segments, which are positioned
in the 1-megabyte address space.
Specifically, there are four segments: Code Segment, Stack Segment, Data Segment, and Extra Segment,
with four segment registers that define the start of the segment: CS, SS, DS, and ES.
An inconvenient part of segment addressing is that if you want to access more than 64K, you need to change the segment register.
So you might push the data segment register, change it temporarily so you can access a new part of memory, and then pop the old data segment
register value off the stack.
This would use the PUSH DS and POP DS instructions.
But why not POP CS?
The 8086 executes code from the code segment, with the instruction pointer (IP) tracking the location in the code segment.
The main problem with POP CS is that it changes the code segment, but not the instruction pointer, so now you are executing
code at the old offset in a new segment.
Unless you line up your code extremely carefully, the result is that you're jumping to an unexpected place in memory.
(Normally, you want to change CS and the instruction pointer at the same time, using a CALL or JMP instruction.)
The second problem with POP CS is prefetching.
For efficiency, the 8086 prefetches instructions before they are needed, storing them in an 6-byte prefetch queue.
When you perform a jump, for instance, the microcode flushes the prefetch queue so execution will continue with the
new instructions, rather than the old instructions.
However, the instructions that pop a segment register don't flush the prefetch buffer.
Thus, POP CS not only jumps to an unexpected location in memory, but it will execute an unpredictable number of instructions
from the old code path.
The POP segment register microcode below packs a lot into three micro-instructions.
The first micro-instruction pops a value from the stack.
Specifically, it moves the stack pointer (SP) to the Indirect (IND) register.
The Indirect register is an internal register, invisible to the programmer, that holds the address offset for memory
accesses.
The first micro-instruction also performs a memory read (R) from the stack segment (SS) and then increments IND
by 2 (P2, plus 2).
The second micro-instruction moves IND to the stack pointer, updating the stack pointer with the new value.
It also tells the microcode engine that this micro-instruction is the next-to-last (NXT) and the next machine instruction
can be started.
The final micro-instruction moves the value read from memory to the appropriate segment register and runs the next instruction.
Specifically, reads and writes put data in the internal OPR (Operand) register.
The hardware uses the register N to indicate the register specified by the instruction.
That is, the value will be stored in the CS, DS, ES, or SS register, depending on the bit pattern in the instruction.
Thus, the same microcode works for all four segment registers.
This is why POP CS works even though POP CS wasn't explicitly implemented in the microcode; it uses the common code.
SP → IND R SS,P2 POP sr: read from stack, compute IND plus 2 IND → SP NXT Put updated value in SP, start next instruction. OPR → N RNI Put stack value in specified segment register
But why does POP CS run this microcode in the first place?
The microcode to execute is selected based on the instruction, but multiple instructions can execute the same microcode.
You can think of the address decoder as pattern-matching on the instruction's bit patterns, where some of the bits can be ignored.
In this case, the POP sr microcode above is run by any instruction with the bit pattern 000??111, where a question mark
can be either a 0 or a 1.
You can verify that this pattern matches POP ES (07), POP SS (17), and POP DS (1F).
However, it also matches 0F, which is why the 0F opcode runs the above microcode and performs POP CS.
In other words, to make 0F do something other than POP CS would require additional circuitry, so it was easier to
leave the action implemented but undocumented.
60-6F: conditional jumps
One whole row of the opcode table is unused: values 60 to 6F.
These opcodes simply act the same as 70 to 7F, the conditional jump instructions.
The conditional jumps use the following microcode.
It fetches the jump offset from the instruction prefetch queue (Q) and puts the value into the ALU's tmpBL register,
the low byte of the tmpB register.
It tests the condition in the instruction (XC) and jumps to the RELJMP micro-subroutine if satisfied.
The RELJMP code (not shown) updates the program counter to perform the jump.
Q → tmpBL Jcond cb: Get offset from prefetch queue JMP XC RELJMP Test condition, if true jump to RELJMP routine RNI No jump: run next instruction
This code is executed for any instruction matching the bit pattern 011?????, i.e. anything from 60 to 7F.
The condition is specified by the four low bits of the instruction.
The result is that any instruction 60-6F is an alias for the corresponding conditional jump 70-7F.
C0, C8: RET/RETF imm
These undocumented opcodes act like a return instruction, specifically RET imm16 (source).
Specifically, the instruction C0 is the same as C2, near return, while C8 is the same as CA, far return.
The microcode below is executed for the instruction bits 1100?0?0, so it is executed for C0, C2, C8, and CA.
It gets two bytes from the instruction prefetch queue (Q) and puts them in the tmpA register.
Next, it calls FARRET, which performs either a near return (popping PC from the stack) or a far return (popping PC and CS
from the stack). Finally, it adds the original argument to the SP, equivalent to popping that many bytes.
Q → tmpAL ADD tmpA RET/RETF iw: Get word from prefetch, set up ADD Q → tmpAH CALL FARRET Call Far Return micro-subroutine IND → tmpB Move SP (in IND) to tmpB for ADD Σ → SP RNI Put sum in Stack Pointer, end
One tricky part is that the FARRET micro-subroutine examines bit 3 of the instruction to determine whether it does a near
return or a far return.
This is why documented instruction C2 is a near return and CA is a far return.
Since C0 and C8 run the same microcode, they will perform the same actions, a near return and a far return respectively.
C1: RET
The undocumented C1 opcode is identical to the documented C3, near return instruction.
The microcode below is executed for instruction bits 110000?1, i.e. C1 and C3.
The first micro-instruction reads from the Stack Pointer, incrementing IND by 2.
Prefetching is suspended and the prefetch queue is flushed, since execution will continue at a new location.
The Program Counter is updated with the value from the stack, read into the OPR register.
Finally, the updated address is put in the Stack Pointer and execution ends.
SP → IND R SS,P2 RET: Read from stack, increment by 2 SUSP Suspend prefetching OPR → PC FLUSH Update PC from stack, flush prefetch queue IND → SP RNI Update SP, run next instruction
C9: RET
The undocumented C9 opcode is identical to the documented CB, far return instruction.
This microcode is executed for instruction bits 110010?1, i.e. C9 and CB, so C9 is identical to CB.
The microcode below simply calls the FARRET micro-subroutine to pop the Program Counter and CS register.
Then the new value is stored into the Stack Pointer.
One subtlety is that FARRET looks at bit 3 of the instruction to switch between a near return and a far return, as
described earlier.
Since C9 and CB both have bit 3 set, they both perform a far return.
CALL FARRET RETF: call FARRET routine
IND → SP RNI Update stack pointer, run next instruction
F1: LOCK prefix
The final hole in the opcode table is F1.
This opcode is different because it is implemented in logic rather than microcode.
The Group Decode ROM indicates that F1 is a prefix, one-byte logic, and LOCK.
The Group Decode outputs are the same as F0, so F1 also acts as a LOCK prefix.
Holes in two-byte opcodes
For most of the 8086 instructions, the first byte specifies the instruction.
However, the 8086 has a few instructions where the second byte specifies the instruction: the reg field of the ModR/M byte provides an opcode extension that selects the instruction.5
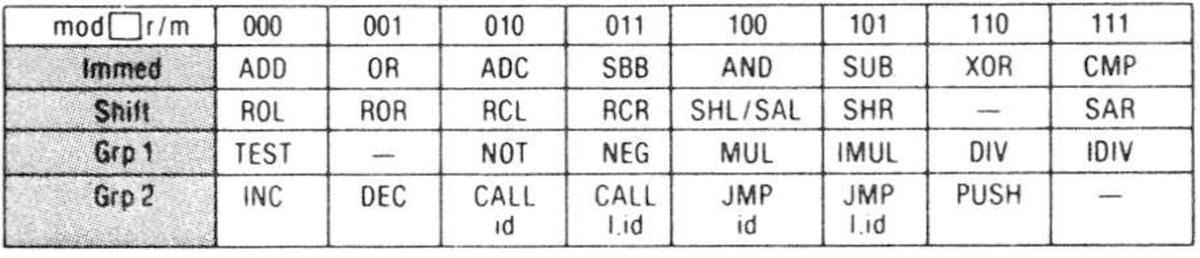
These fall into four categories which Intel labeled "Immed", "Shift", "Group 1", and "Group 2", corresponding to opcodes 80-83, D0-D3,
F6-F7, and FE-FF.
The table below shows how the second byte selects the instruction.
Note that "Shift", "Group 1", and "Group 2" all have gaps, resulting in undocumented values.
These sets of instructions are implemented in two completely different ways.
The "Immed" and "Shift" instructions run microcode in the standard way, selected by the first byte.
For a typical arithmetic/logic instruction such as ADD, bits 5-3 of the first instruction byte are latched into the X register to indicate
which ALU operation to perform.
The microcode specifies a generic ALU operation, while the X register controls whether the operation is an ADD, SUB, XOR, or
so forth.
However, the Group Decode ROM indicates that for the special "Immed" and "Shift" instructions, the X register latches the bits
from the second byte.
Thus, when the microcode executes a generic ALU operation, it ends up with the one specified in the second byte.6
The "Group 1" and "Group 2" instructions (F0-F1, FE-FF), however, run different microcode for each instruction.
Bits 5-3 of the second byte replace bits 2-0 of the instruction before executing the microcode.
Thus, F0 and F1 act as if they are opcodes in the range F0-F7, while FE and FF act as if they are opcodes in the range F8-FF.
Thus, each instruction specified by the second byte can have its own microcode, unlike the "Immed" and "Shift" instructions.
The trick that makes this work is that all the "real" opcodes in the range F0-FF are implemented in logic, not microcode,
so there are no collisions.
The hole in "Shift": SETMO, D0..D3/6
There is a "hole" in the list of shift operations when the second byte has the bits 110 (6).
(This is typically expressed as D0/6 and so forth; the value after the slash is the opcode-selection bits in the ModR/M byte.)
Internally, this value selects the ALU's SETMO (Set Minus One) operation, which simply returns FF or FFFF, for a byte or word operation respectively.7
The microcode below is executed for 1101000? bit patterns patterns (D0 and D1).
The first instruction gets the value from the M register and sets up the ALU to do whatever operation was
specified in the instruction (indicated by XI).
Thus, the same microcode is used for all the "Shift" instructions, including SETMO.
The result is written back to M. If no writeback to memory is required (NWB), then RNI runs the next instruction, ending
the microcode sequence.
However, if the result is going to memory, then the last line writes the value to memory.
M → tmpB XI tmpB, NXT rot rm, 1: get argument, set up ALU Σ → M NWB,RNI F Store result, maybe run next instruction W DS,P0 RNI Write result to memory
The D2 and D3 instructions (1101001?) perform a variable number of shifts, specified by the CL register, so they use different microcode (below).
This microcode loops the number of times specified by CL, but the control flow is a bit tricky to avoid shifting if
the intial counter value is 0.
The code sets up the ALU to pass the counter (in tmpA) unmodified the first time (PASS) and jumps to 4, which
updates the counter and sets up the ALU for the shift operation (XI).
If the counter is not zero, it jumps back to 3, which performs the previously-specified shift and sets up
the ALU to decrement the counter (DEC).
This time, the code at 4 decrements the counter.
The loop continues until the counter reaches zero. The microcode stores the result as in the previous microcode.
ZERO → tmpA rot rm,CL: 0 to tmpA CX → tmpAL PASS tmpA Get count to tmpAL, set up ALU to pass through M → tmpB JMPS 4 Get value, jump to loop (4) Σ → tmpB DEC tmpA F 3: Update result, set up decrement of count Σ → tmpA XI tmpB 4: update count in tmpA, set up ALU JMPS NZ 3 Loop if count not zero tmpB → M NWB,RNI Store result, maybe run next instruction W DS,P0 RNI Write result to memory
The hole in "group 1": TEST, F6/1 and F7/1
The F6 and F7 opcodes are in "group 1", with the specific instruction specified by bits 5-3 of the second byte.
The second-byte table showed a hole for the 001 bit sequence.
As explained earlier, these bits replace the low-order bits of the instruction, so F6 with 001 is processed as if it were
the opcode F1.
The microcode below matches against instruction bits 1111000?, so F6/1 and F7/1 have the same effect as F6/0 and F7/1 respectively,
that is, the byte and word TEST instructions.
The microcode below gets one or two bytes from the prefetch queue (Q); the L8 condition tests if the operation is
an 8-bit (i.e. byte) operation and skips the second micro-instruction.
The third micro-instruction ANDs the argument and the fetched value.
The condition flags (F) are set based on the result, but the result itself is discarded.
Thus, the TEST instruction tests a value against a mask, seeing if any bits are set.
Q → tmpBL JMPS L8 2 TEST rm,i: Get byte, jump if operation length = 8 Q → tmpBH Get second byte from the prefetch queue M → tmpA AND tmpA, NXT 2: Get argument, AND with fetched value Σ → no dest RNI F Discard result but set flags.
I explained the processing of these "Group 3" instructions in more detail in my microcode article.
The hole in "group 2": PUSH, FE/7 and FF/7
The FE and FF opcodes are in "group 2", which has a hole for the 111 bit sequence in the second byte.
After replacement, this will be processed as the FF opcode, which matches the pattern 1111111?.
In other words, the instruction will be processed the same as the 110 bit pattern, which is PUSH.
The microcode gets the Stack Pointer, sets up the ALU to decrement it by 2.
The new value is written to SP and IND. Finally, the register value is written to stack memory.
SP → tmpA DEC2 tmpA PUSH rm: set up decrement SP by 2 Σ → IND Decremented SP to IND Σ → SP Decremented SP to SP M → OPR W SS,P0 RNI Write the value to memory, done
82 and 83 "Immed" group
Opcodes 80-83 are the "Immed" group, performing one of eight arithmetic operations, specified in the ModR/M byte.
The four opcodes differ in the size of the values: opcode 80 applies an 8-bit immediate value to an 8-bit register, 81 applies a 16-bit
value to a 16-bit register, 82 applies an 8-bit value to an 8-bit register, and 83 applies an 8-bit value to a 16-bit register.
The opcode 82 has the strange situation that some sources say it is undocumented, but it shows up in some Intel documentation as a valid bit combination (e.g. below).
Note that 80 and 82 have the 8-bit to 8-bit action, so the 82 opcode is redundant.
The microcode below is used for all four opcodes.
If the ModR/M byte specifies memory, the appropriate micro-subroutine is called to compute the effective address in IND,
and fetch the byte or word into OPR.
The first two instructions below get the two immediate data bytes from the prefetch queue; for an 8-bit operation, the second byte
is skipped.
Next, the second argument M is loaded into tmpA and the desired ALU operation (XI) is configured.
The result Σ is stored into the specified register M and the operation may terminate with RNI.
But if the ModR/M byte specified memory, the following write micro-operation saves the value to memory.
Q → tmpBL JMPS L8 2 alu rm,i: get byte, test if 8-bit op Q → tmpBH Maybe get second byte M → tmpA XI tmpA, NXT 2: Σ → M NWB,RNI F Save result, update flags, done if no memory writeback W DS,P0 RNI Write result to memory if needed
The tricky part of this is the L8 condition, which tests if the operation is 8-bit.
You might think that bit 0 acts as the byte/word bit in a nice, orthogonal way, but the 8086 has a bunch of special cases.
Bit 0 of the instruction typically selects between a byte and a word operation, but there are a bunch of special cases.
The Group Decode ROM creates a signal indicating if bit 0 should be used as the byte/word bit.
But it generates a second signal indicating that an instruction should be forced to operate on bytes, for instructions
such as DAA and XLAT.
Another Group Decode ROM signal indicates that bit 3 of the instruction should select byte or word; this
is used for the MOV instructions with opcodes Bx.
Yet another Group Decode ROM signal indicates that inverted bit 1 of the instruction should select byte or word;
this is used for a few opcodes, including 80-87.
The important thing here is that for the opcodes under discussion (80-83), the L8 micro-condition uses both bits 0 and 1
to determine if the instruction is 8 bits or not.
The result is that only opcode 81 is considered 16-bit by the L8 test, so it is the only one that uses two immediate bytes
from the instruction.
However, the register operations use only bit 0 to select a byte or word transfer.
The result is that opcode 83 has the unusual behavior of using an 8-bit immediate operand with a 16-bit register.
In this case, the 8-bit value is sign-extended to form a 16-bit value. That is, the top bit of the 8-bit value fills
the entire upper half of the 16-bit value,
converting an 8-bit signed value to a 16-bit signed value (e.g. -1 is FF, which becomes FFFF).
This makes sense for arithmetic operations, but not much sense for logical operations.
Intel documentation is inconsistent about which opcodes are listed for which instructions.
Intel opcode maps generally define opcodes 80-83.
However, lists of specific instructions show opcodes 80, 81, and 83 for arithmetic operations but only 80 and 81 for logical operations.8
That is, Intel omits the redundant 82 opcode as well as omitting logic operations that perform sign-extension (83).
More FE holes
For the "group 2" instructions, the FE opcode performs a byte operation while FF performs a word operation.
Many of these operations don't make sense for bytes: CALL, JMP, and PUSH.
(The only instructions supported for FE are INC and DEC.) But what happens if you use the unsupported instructions?
The remainder of this section examines those cases and shows that the results are not useful.
CALL: FE/2
This instruction performs an indirect subroutine call within a segment, reading the target address from the memory location specified by the ModR/M byte.
The microcode below is a bit convoluted because the code falls through into the shared NEARCALL routine, so there is
some unnecessary register movement.
Before this microcode executes, the appropriate ModR/M micro-subroutine will read the target address from memory.
The code below copies the destination address from M to tmpB and stores it into the PC later in the code
to transfer execution.
The code suspends prefetching, corrects the PC to cancel the offset from prefetching, and flushes the prefetch queue.
Finally, it decrements the SP by two and writes the old PC to the stack.
M → tmpB SUSP CALL rm: read value, suspend prefetch SP → IND CORR Get SP, correct PC PC → OPR DEC2 tmpC Get PC to write, set up decrement tmpB → PC FLUSH NEARCALL: Update PC, flush prefetch IND → tmpC Get SP to decrement Σ → IND Decremented SP to IND Σ → SP W SS,P0 RNI Update SP, write old PC to stack
This code will mess up in two ways when executed as a byte instruction. First, when the destination address is read from memory, only a byte will be read, so the destination address will be corrupted. (I think that the behavior here depends on the bus hardware. The 8086 will ask for a byte from memory but will read the word that is placed on the bus. Thus, if memory returns a word, this part may operate correctly. The 8088's behavior will be different because of its 8-bit bus.) The second issue is writing the old PC to the stack because only a byte of the PC will be written. Thus, when the code returns from the subroutine call, the return address will be corrupt.
CALL: FE/3
This instruction performs an indirect subroutine call between segments, reading the target address from the memory location specified by the ModR/M byte.
IND → tmpC INC2 tmpC CALL FAR rm: set up IND+2 Σ → IND R DS,P0 Read new CS, update IND OPR → tmpA DEC2 tmpC New CS to tmpA, set up SP-2 SP → tmpC SUSP FARCALL: Suspend prefetch Σ → IND CORR FARCALL2: Update IND, correct PC CS → OPR W SS,M2 Push old CS, decrement IND by 2 tmpA → CS PASS tmpC Update CS, set up for NEARCALL PC → OPR JMP NEARCALL Continue with NEARCALL
As in the previous CALL, this microcode will fail in multiple ways when executed in byte mode.
The new CS and PC addresses will be read from memory as bytes, which may or may not work.
Only a byte of the old CS and PC will be pushed to the stack.
JMP: FE/4
This instruction performs an indirect jump within a segment, reading the target address from the memory location specified by the ModR/M byte.
The microcode is short, since the ModR/M micro-subroutine does most of the work.
I believe this will have the same problem as the previous CALL instructions, that it will attempt to read a byte from
memory instead of a word.
SUSP JMP rm: Suspend prefetch
M → PC FLUSH RNI Update PC with new address, flush prefetch, done
JMP: FE/5
This instruction performs an indirect jump between segments, reading the new PC and CS values from the memory location specified by the ModR/M byte.
The ModR/M micro-subroutine reads the new PC address. This microcode increments IND and suspends prefetching.
It updates the PC, reads the new CS value from memory, and updates the CS.
As before, the reads from memory will read bytes instead of words, so this code will not meaningfully work in byte mode.
IND → tmpC INC2 tmpC JMP FAR rm: set up IND+2 Σ → IND SUSP Update IND, suspend prefetch tmpB → PC R DS,P0 Update PC, read new CS from memory OPR → CS FLUSH RNI Update CS, flush prefetch, done
PUSH: FE/6
This instruction pushes the register or memory value specified by the ModR/M byte. It decrements the SP by 2 and then writes the value to the stack. It will write one byte to the stack but decrements the SP by 2, so one byte of old stack data will be on the stack along with the data byte.
SP → tmpA DEC2 tmpA PUSH rm: Set up SP decrement Σ → IND Decremented value to IND Σ → SP Decremented value to SP M → OPR W SS,P0 RNI Write the data to the stack
Undocumented instruction values
The next category of undocumented instructions is where the first byte indicates a valid instruction, but there is something wrong with the second byte.
AAM: ASCII Adjust after Multiply
The AAM instruction is a fairly obscure one, designed to support binary-coded decimal
arithmetic (BCD).
After multiplying two BCD digits, you end up with a binary value between 0 and 81 (0×0 to 9×9).
If you want a BCD result, the AAM instruction converts this binary value to BCD, for instance splitting 81 into the
decimal digits 8 and 1, where the upper digit is 81 divided by 10, and the lower digit is 81 modulo 10.
The interesting thing about AAM is that the 2-byte instruction is D4 0A. You might notice that hex 0A is 10, and this
is not a coincidence.
There wasn't an easy way to get the value 10 in the microcode, so instead they made the instruction
provide that value in the second byte.
The undocumented (but well-known) part is that if you provide a value other than 10, the instruction will convert the binary input into
digits in that base. For example, if you provide 8 as the second byte, the instruction returns the value divided by 8
and the value modulo 8.
The microcode for AAM, below, sets up the registers. calls
the CORD (Core Division) micro-subroutine to perform the division,
and then puts the results into AH and AL.
In more detail, the CORD routine divides tmpA/tmpC by tmpB, putting the complement of the quotient in tmpC and leaving the remainder in tmpA.
(If you want to know how CORD works internally, see my division post.)
The important step is that the AAM microcode gets the divisor from the prefetch queue (Q).
After calling CORD, it sets up the ALU to perform a 1's complement of tmpC and puts the result (Σ) into AH.
It sets up the ALU to pass tmpA through unchanged, puts the result (Σ) into AL, and updates the flags accordingly (F).
Q → tmpB AAM: Move byte from prefetch to tmpB ZERO → tmpA Move 0 to tmpA AL → tmpC CALL CORD Move AL to tmpC, call CORD. COM1 tmpC Set ALU to complement Σ → AH PASS tmpA, NXT Complement AL to AH Σ → AL RNI F Pass tmpA through ALU to set flags
The interesting thing is why this code has undocumented behavior.
The 8086's microcode only has support for the constants 0 and all-1's (FF or FFFF), but the microcode needs to divide by 10.
One solution would be to implement an additional micro-instruction and more circuitry to provide the constant 10, but every
transistor was precious back then.
Instead, the designers took the approach of simply putting the number 10 as the second byte of the instruction and loading the
constant from there.
Since the AAM instruction is not used very much, making the instruction two bytes long wasn't much of a drawback.
But if you put a different number in the second byte, that's the divisor the microcode will use.
(Of course you could add circuitry to verify that the number is 10, but then the implementation is no longer simple.)
Intel could have documented the full behavior, but that creates several problems. First, Intel would be stuck supporting the full behavior into the future. Second, there are corner cases to deal with, such as divide-by-zero. Third, testing the chip would become harder because all these cases would need to be tested. Fourth, the documentation would become long and confusing. It's not surprising that Intel left the full behavior undocumented.
AAD: ASCII Adjust before Division
The AAD instruction is analogous to AAM but used for BCD division.
In this case, you want to divide a two-digit BCD number by something, where the BCD digits are in AH and AL.
The AAD instruction converts the two-digit BCD number to binary by computing AH×10+AL, before you perform
the division.
The microcode for AAD is shown below. The microcode sets up the registers, calls the multiplication micro-subroutine
CORX (Core Times), and
then puts the results in AH and AL.
In more detail, the multiplier comes from the instruction prefetch queue Q.
The CORX routine multiples tmpC by tmpB, putting the result in tmpA/tmpC.
Then the microcode adds the low BCD digit (AL) to the product (tmpB + tmpC), putting the sum (Σ) into AL,
clearing AH and setting the status flags F appropriately.
One interesting thing is that the second-last micro-instruction jumps to AAEND, which is the last
micro-instruction of the AAM microcode above.
By reusing the micro-instruction from AAM, the microcode is one micro-instruction shorter, but
the jump adds one cycle to the execution time.
(The CORX routine is used for integer multiplication; I discuss the internals in this post.)
Q → tmpC AAD: Get byte from prefetch queue. AH → tmpB CALL CORX Call CORX AL → tmpB ADD tmpC Set ALU for ADD ZERO → AH JMP AAEND Zero AH, jump to AAEND i ... Σ → AL RNI F AAEND: Sum to AL, done.
As with AAM, the constant 10 is provided in the second byte of the instruction.
The microcode accepts any value here, but values other than 10 are undocumented.
8C, 8E: MOV sr
The opcodes 8C and 8E perform a MOV register to or from the specified segment register, using the register specification
field in the ModR/M byte.
There are four segment registers and three selection bits, so an invalid segment register can be specified.
However, the hardware that decodes the register number ignores instruction bit 5 for a segment register. Thus,
specifying a segment register 4 to 7 is the same as specifying a segment register 0 to 3.
For more details, see my article on 8086 register codes.
Unexpected REP prefix
REP IMUL / IDIV
The REP prefix is used with string operations to cause the operation to be repeated across a block of memory.
However, if you use this prefix with an IMUL or IDIV instruction, it has the unexpected behavior
of negating the product or the quotient (source).
The reason for this behavior is that the string operations use an internal flag called F1 to indicate that a REP
prefix has been applied.
The multiply and divide code reuses this flag to track the sign of the input values, toggling F1 for each negative value.
If F1 is set, the value at the end is negated. (This handles "two negatives make a positive.")
The consequence is that the REP prefix puts the flag in the 1 state when the multiply/divide starts, so the computed sign
will be wrong at the end and the result is the negative of the expected result.
The microcode is fairly complex, so I won't show it here; I explain it in detail in this blog post.
REP RET
Wikipedia lists
REP RET (i.e. RET with a REP prefix) as a way to implement a two-byte return instruction.
This is kind of trivial; the RET microcode (like almost every instruction) doesn't use the F1 internal flag,
so the REP prefix has no effect.
REPNZ MOVS/STOS
Wikipedia mentions that
the use of the REPNZ prefix (as opposed to REPZ) is undefined with string operations other than CMPS/SCAS.
An internal flag called F1Z distinguishes between the REPZ and REPNZ prefixes.
This flag is only used by CMPS/SCAS. Since the other string instructions ignore this flag, they will ignore the
difference between REPZ and REPNZ.
I wrote about string operations in more detail in this post.
Using a register instead of memory.
Some instructions are documented as requiring a memory operand. However, the ModR/M byte can specify a register. The behavior in these cases can be highly unusual, providing access to hidden registers. Examining the microcode shows how this happens.
LEA reg
Many instructions have a ModR/M byte that indicates the memory address that the instruction should use, perhaps through
a complicated addressing mode.
The LEA (Load Effective Address) instruction is different: it doesn't access the memory location but returns the address itself.
The undocumented part is that the ModR/M byte can specify a register instead of a memory location. In that case,
what does the LEA instruction do? Obviously it can't return the address of a register, but it needs to return something.
The behavior of LEA is explained by how the 8086 handles the ModR/M byte.
Before running the microcode corresponding to the instruction, the microcode engine calls a short micro-subroutine
for the particular addressing mode.
This micro-subroutine puts the desired memory address (the effective address) into the tmpA register.
The effective address is copied to the IND (Indirect) register and the value is loaded from memory if needed.
On the other hand, if the ModR/M byte specified a register instead of memory, no micro-subroutine is called.
(I explain ModR/M handling in more detail in this article.)
The microcode for LEA itself is just one line. It stores the effective address in the IND register into the specified destination register, indicated by N.
This assumes that the appropriate ModR/M micro-subroutine was called before this code, putting the effective address into IND.
IND → N RNI LEA: store IND register in destination, done
But if a register was specified instead of a memory location, no ModR/M micro-subroutine gets called.
Instead, the LEA instruction will return whatever value was left
in IND from before, typically the previous memory location that was accessed.
Thus, LEA can be used to read the value of the IND register, which is normally hidden from the programmer.
LDS reg, LES reg
The LDS and LES instructions load a far pointer from memory into the specified segment register and general-purpose register.
The microcode below assumes that the appropriate ModR/M micro-subroutine has set up IND and read the first value into OPR.
The microcode updates the destination register, increments IND by 2, reads the next value, and updates DS.
(The microcode for LES is a copy of this, but updates ES.)
OPR → N LDS: Copy OPR to dest register IND → tmpC INC2 tmpC Set up incrementing IND by 2 Σ → IND R DS,P0 Update IND, read next location OPR → DS RNI Update DS
If the LDS instruction specifies a register instead of memory, a micro-subroutine will not be called, so IND and OPR
will have values from a previous instruction.
OPR will be stored in the destination register, while the DS value will be read from the address IND+2.
Thus, these instructions provide a mechanism to access the hidden OPR register.
JMP FAR rm
The JMP FAR rm instruction normally jumps to the far address stored in memory at the location indicated by the ModR/M byte.
(That is, the ModR/M byte indicates where the new PC and CS values are stored.)
But, as with LEA, the behavior is undocumented if the ModR/M byte specifies a register, since a register doesn't hold
a four-byte value.
The microcode explains what happens.
As with LEA, the code expects a micro-subroutine to put the address into the IND register.
In this case, the micro-subroutine also loads the value at that address (i.e. the destination PC) into tmpB.
The microcode increments IND by 2 to point to the CS word in memory and reads that into CS.
Meanwhile, it updates the PC with tmpB.
It suspends prefetching and flushes the queue, so instruction fetching will restart at the new address.
IND → tmpC INC2 tmpC JMP FAR rm: set up to add 2 to IND Σ → IND SUSP Update IND, suspend prefetching tmpB → PC R DS,P0 Update PC with tmpB. Read new CS from specified address OPR → CS FLUSH RNI Update CS, flush queue, done
If you specify a register instead of memory, the micro-subroutine won't get called.
Instead, the program counter will be loaded with whatever value was in tmpB and the CS segment register will
be loaded from the memory location two bytes after the location that IND was referencing.
Thus, this undocumented use of the instruction gives access to the otherwise-hidden tmpB register.
The end of undocumented instructions
Microprocessor manufacturers soon realized that undocumented instructions were a problem, since programmers find them and often use them. This creates an issue for future processors, or even revisions of the current processor: if you eliminate an undocumented instruction, previously-working code that used the instruction will break, and it will seem like the new processor is faulty.
The solution was for processors to detect undocumented instructions and prevent them from executing. By the early 1980s, processors had enough transistors (thanks to Moore's law) that they could include the circuitry to block unsupported instructions. In particular, the 80186/80188 and the 80286 generated a trap of type 6 when an unused opcode was executed, blocking use of the instruction.9 This trap is also known as #UD (Undefined instruction trap).10
Conclusions
The 8086, like many early microprocessors, has undocumented instructions but no traps to stop them from executing.11
For the 8086, these fall into several categories.
Many undocumented instructions simply mirror existing instructions.
Some instructions are implemented but not documented for one reason or another, such as SALC and POP CS.
Other instructions can be used outside their normal range, such as AAM and AAD.
Some instructions are intended to work only with a memory address, so specifying a register can have
strange effects such as revealing the values of the hidden IND and OPR registers.
Keep in mind that my analysis is based on transistor-level simulation and examining the microcode; I haven't verified the behavior on a physical 8086 processor. Please let me know if you see any errors in my analysis or undocumented instructions that I have overlooked. Also note that the behavior could change between different versions of the 8086; in particular, some versions by different manufacturers (such as the NEC V20 and V30) are known to be different.
I plan to write more about the 8086, so follow me on Twitter @kenshirriff or RSS for updates. I've also started experimenting with Mastodon recently as @[email protected] and Bluesky as @righto.com so you can follow me there too.
Notes and references
-
The 6502 processor, for instance, has illegal instructions with various effects, including causing the processor to hang. The article How MOS 6502 illegal opcodes really work describes in detail how the instruction decoding results in various illegal opcodes. Some of these opcodes put the internal bus into a floating state, so the behavior is electrically unpredictable. ↩
-
The 8086 used up almost all the single-byte opcodes, which made it difficult to extend the instruction set. Most of the new instructions for the 386 or later are multi-byte opcodes, either using
0Fas a prefix or reusing the earlier REP prefix (F3). Thus, the x86 instruction set is less efficient than it could be, since many single-byte opcodes were "wasted" on hardly-used instructions such as BCD arithmetic, forcing newer instructions to be multi-byte. ↩ -
For details on the "magic instruction" hidden in the 8086 microcode, see NEC v. Intel: Will Hardware Be Drawn into the Black Hole of Copyright Editors page 49. I haven't found anything stating that
SALCwas the hidden instruction, but this is the only undocumented instruction that makes sense as something deliberately put into the microcode. The court case is complicated since NEC had a licensing agreement with Intel, so I'm skipping lots of details. See NEC v. Intel: Breaking new ground in the law of copyright for more. ↩ -
The microcode listings are based on Andrew Jenner's disassembly. I have made some modifications to (hopefully) make it easier to understand. ↩
-
Specifying the instruction through the ModR/M reg field may seem a bit random, but there's a reason for this. A typical instruction such as
ADDhas two arguments specified by the ModR/M byte. But other instructions such as shift instructions orNOTonly take one argument. For these instructions, the ModR/Mregfield would be wasted if it specified a register. Thus, using theregfield to specify instructions that only use one argument makes the instruction set more efficient. ↩ -
Note that "normal" ALU operations are specified by bits 5-3 of the instruction; in order these are
ADD,OR,ADC,SBB,AND,SUB,XOR, andCMP. These are exactly the same ALU operations that the "Immed" group performs, specified by bits 5-3 of the second byte. This illustrates how the same operation selection mechanism (theXregister) is used in both cases. Bit 6 of the instruction switches between the set of arithmetic/logic instructions and the set of shift/rotate instructions. ↩ -
As far as I can tell, SETMO isn't used by the microcode. Thus, I think that SETMO wasn't deliberately implemented in the ALU, but is a consequence of how the ALU's control logic is implemented. That is, all the even entries are left shifts and the odd entries are right shifts, so operation 6 activates the left-shift circuitry. But it doesn't match a specific left shift operation, so the ALU doesn't get configured for a "real" left shift. In other words, the behavior of this instruction is due to how the ALU handles a case that it wasn't specifically designed to handle.
This function is implemented in the ALU somewhat similar to a shift left. However, instead of passing each input bit to the left, the bit from the right is passed to the left. That is, the input to bit 0 is shifted left to all of the bits of the result. By setting this bit to 1, all bits of the result are set, yielding the minus 1 result. ↩
-
This footnote provides some references for the "Immed" opcodes. The 8086 datasheet has an opcode map showing opcodes
80through83as valid. However, in the listings of individual instructions it only shows80and81for logical instructions (i.e. bit 1 must be 0), while it shows80-83for arithmetic instructions. The modern Intel 64 and IA-32 Architectures Software Developer's Manual is also contradictory. Looking at the instruction reference forAND(Vol2A3-78), for instance, shows opcodes80,81, and83, explicitly labeling83as sign-extended. But the opcode map (Table A-2 Vol2DA-7) shows80-83as defined except for82in64-bit mode. The instruction bit diagram (Table B-13Vol2DB-7) shows80-83valid for the arithmetic and logical instructions. ↩ -
The 80286 was more thorough about detecting undefined opcodes than the 80186, even taking into account the differences in instruction set. The 80186 generates a trap when
0F,63-67,F1, orFFFFis executed. The 80286 generates invalid opcode exception number 6 (#UD) on any undefined opcode, handling the following cases:- The first byte of an instruction is completely invalid (e.g., 64H).
- The first byte indicates a 2-byte opcode and the second byte is invalid (e.g., 0F followed by 0FFH).
- An invalid register is used with an otherwise valid opcode (e.g., MOV CS,AX).
- An invalid opcode extension is given in the REG field of the ModR/M byte (e.g., 0F6H /1).
- A register operand is given in an instruction that requires a memory operand (e.g., LGDT AX).
-
In modern x86 processors, most undocumented instructions cause faults. However, there are still a few undocumented instructions that don't fault. These may be for internal use or corner cases of documented instructions. For details, see Breaking the x86 Instruction Set, a video from Black Hat 2017. ↩
-
Several sources have discussed undocumented 8086 opcodes before. The article Undocumented 8086 Opcodes describes undocumented opcodes in detail. Wikipedia has a list of undocumented x86 instructions. The book Undocumented PC discusses undocumented instructions in the 8086 and later processors. This StackExchange Retrocomputing post describes undocumented instructions. These Hacker News comments discuss some undocumented instructions. There are other sources with more myth than fact, claiming that the 8086 treats undocumented instructions as NOPs, for instance. ↩