Inside the mechanical Bendix Air Data Computer, part 5: motor/tachometers

The Bendix Central Air Data Computer (CADC) is an electromechanical analog computer that uses gears and cams for its mathematics. It was a key part of military planes such as the F-101 and the F-111 fighters, computing airspeed, Mach number, and other "air data". The rotating gears are powered by six small servomotors, so these motors are in a sense the fundamental component of the CADC. In the photo below, you can see one of the cylindrical motors near the center, about 1/3 of the way down.

The servomotors in the CADC are unlike standard motors. Their name—"Motor-Tachometer Generator" or "Motor and Rate Generator"1—indicates that each unit contains both a motor and a speed sensor. Because the motor and generator use two-phase signals, there are a total of eight colorful wires coming out, many more than a typical motor. Moreover, the direction of the motor can be controlled, unlike typical AC motors. I couldn't find a satisfactory explanation of how these units worked, so I bought one and disassembled it. This article (part 5 of my series on the CADC2) provides a complete teardown of the motor/generator and explain how it works.

The Bendix MG-1A Central Air Data Computer with the case removed, showing the compact gear mechanisms inside. Click this image (or any other) for a larger version.

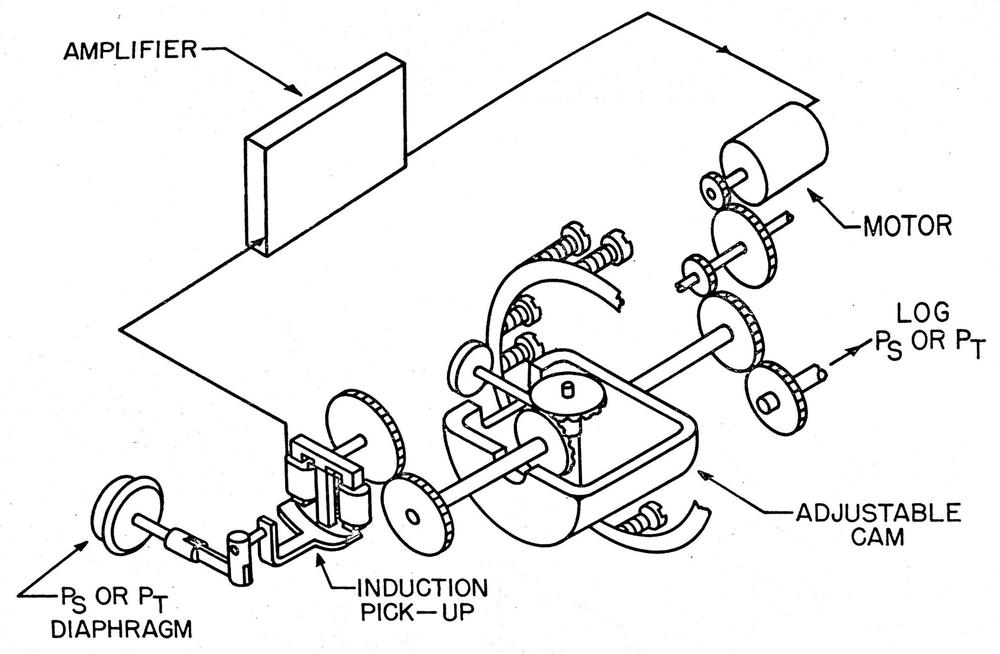
The image below shows a closeup of two motors powering one of the pressure signal outputs. Note the bundles of colorful wires to each motor, entering in two locations. At the top, the motors drive complex gear trains. The high-speed motors are geared down by the gear trains to provide much slower rotations with sufficient torque to power the rest of the CADC's mechanisms.

Two motor/generators in the pressure section of the CADC. The one at the back is mostly hidden.

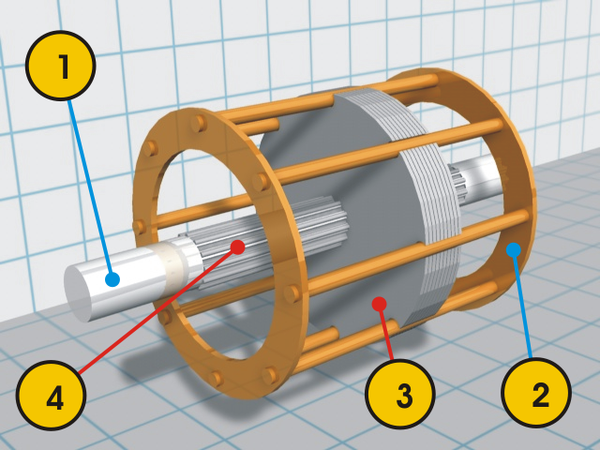
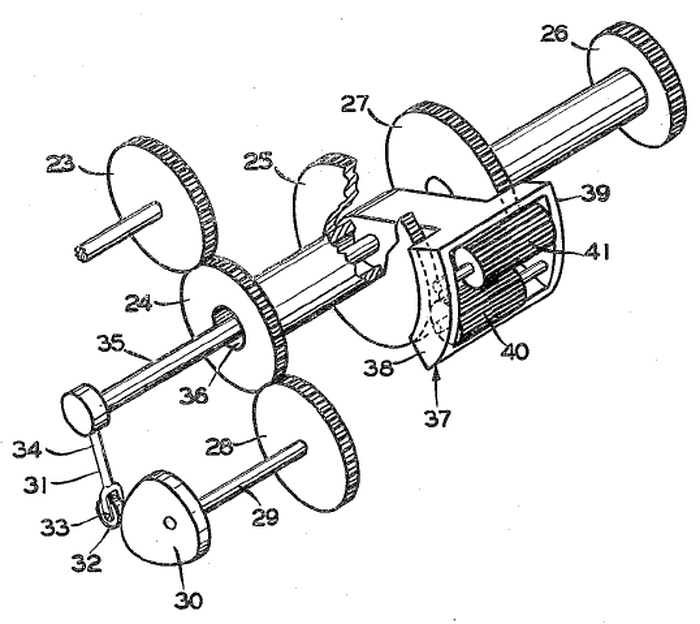
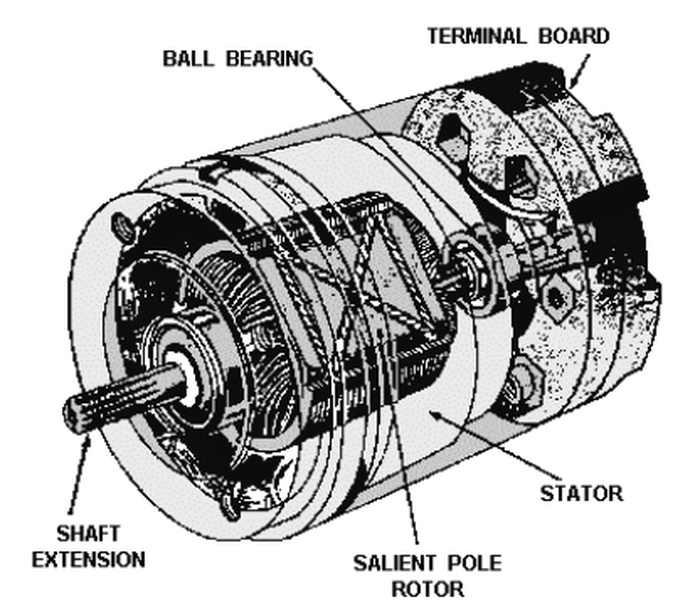
The motor/tachometer that we disassembled is shorter than the ones in the CADC (despite having the same part number), but the principles are the same. We started by removing a small C-clip on the end of the motor and and unscrewing the end plate. The unit is pretty simple mechanically. It has bearings at each end for the rotor shaft. There are four wires for the motor and four wires for the tachometer.3

The motor disassembled to show the internal components.

The rotor (below) has two parts on the shaft. the left part is for the motor and the right drum is for the tachometer. The left part is a squirrel-cage rotor4 for the motor. It consists of conducting bars (light-colored) on an iron core. The conductors are all connected at both ends by the conductive rings at either end. The metal drum on the right is used by the tachometer. Note that there are no electrical connections between the rotor components and the rest of the motor: there are no brushes or slip rings. The interaction between the rotor and the windings in the body of the motor is purely magnetic, as will be explained.

The rotor and shaft.

The motor/tachometer contains two cylindrical stators that create the magnetic fields, one for the motor and one for the tachometer. The photo below shows the motor stator inside the unit after removing the tachometer stator. The stators are encased in hard green plastic and tightly pressed inside the unit. In the center, eight metal poles are visible. They direct the magnetic field onto the rotor.

Inside the motor after removing the tachometer winding.

The photo below shows the stator for the tachometer, similar to the stator for the motor. Note the shallow notches that look like black lines in the body on the lower left. These are probably adjustments to the tachometer during manufacturing to compensate for imperfections. The adjustments ensure that the magnetic fields are nulled out so the tachometer returns zero voltage when stationary. The metal plate on top shields the tachometer from the motor's magnetic fields.

The stator for the tachometer.

The poles and the metal case of the stator look solid, but they are not. Instead, they are formed from a stack of thin laminations. The reason to use laminations instead of solid metal is to reduce eddy currents in the metal. Each lamination is varnished, so it is insulated from its neighbors, preventing the flow of eddy currents.

One lamination from the stack of laminations that make up the winding. The lamination suffered some damage during disassembly; it was originally round.

In the photo below, I removed some of the plastic to show the wire windings underneath. The wires look like bare copper, but they have a very thin layer of varnish to insulate them. There are two sets of windings (orange and blue, or red and black) around alternating metal poles. Note that the wires run along the pole, parallel to the rotor, and then wrap around the pole at the top and bottom, forming oblong coils around each pole.5 This generates a magnetic field through each pole.

Removing the plastic reveals the motor windings.

The motor

The motor part of the unit is a two-phase induction motor with a squirrel-cage rotor.6 There are no brushes or electrical connections to the rotor, and there are no magnets, so it isn't obvious what makes the rotor rotate. The trick is the "squirrel-cage" rotor, shown below. It consists of metal bars that are connected at the top and bottom by rings. Assume (for now) that the fixed part of the motor, the stator, creates a rotating magnetic field. The important principle is that a changing magnetic field will produce a current in a wire loop.7 As a result, each loop in the squirrel-cage rotor will have an induced current: current will flow up9 the bars facing the north magnetic field and down the south-facing bars, with the rings on the end closing the circuits.

A squirrel-cage rotor. The numbered parts are (1) shaft, (2) end cap, (3) laminations, and (4) splines to hold the laminations. Image from Robo Blazek.

But how does the stator produce a rotating magnetic field? And how do you control the direction of rotation? The next important principle is that current flowing through a wire produces a magnetic field.8 As a result, the currents in the squirrel cage rotor produce a magnetic field perpendicular to the cage. This magnetic field causes the rotor to turn in the same direction as the stator's magnetic field, driving the motor. Because the rotor is powered by the induced currents, the motor is called an induction motor.

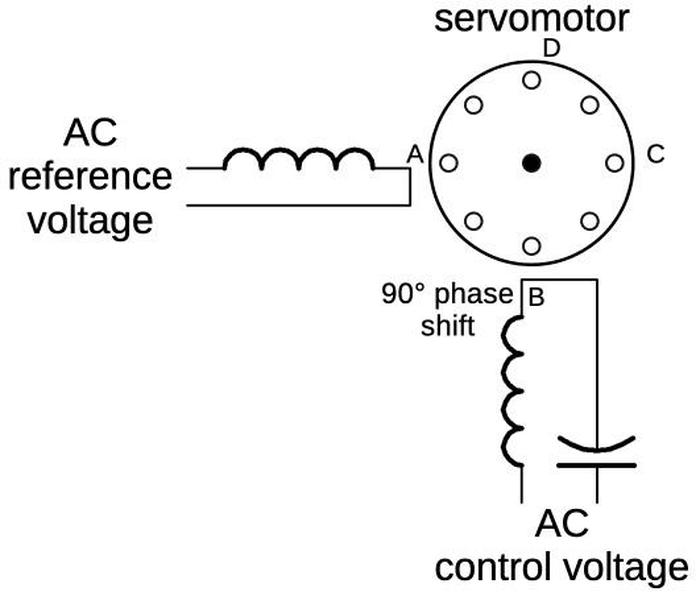
The diagram below shows how the motor is wired, with a control winding and a reference winding. Both windings are powered with AC, but the control voltage either lags the reference winding by 90° or leads the reference winding by 90°, due to the capacitor. Suppose the current through the control winding lags by 90°. First, the reference voltage's sine wave will have a peak, producing the magnetic field's north pole at A. Next (90° later), the control voltage will peak, producing the north pole at B. The reference voltage will go negative, producing a south pole at A and thus a north pole at C. The control voltage will go negative, producing a south pole at B and a north pole at D. This cycle will repeat, with the magnetic field rotating counter-clockwise from A to D. Conversely, if the control voltage leads the reference voltage, the magnetic field will rotate clockwise. This causes the motor to spin in one direction or the other, with the direction controlled by the control voltage. (The motor has four poles for each winding, rather than the one shown below; this increases the torque and reduces the speed.)

Diagram showing the servomotor wiring.

The purpose of the capacitor is to provide the 90° phase shift so the reference voltage and the control voltage can be driven from the same single-phase AC supply (in this case, 26 volts, 400 hertz). Switching the polarity of the control voltage reverses the direction of the motor.

There are a few interesting things about induction motors. You might expect that the motor would spin at the same rate as the rotating magnetic field. However, this is not the case. Remember that a changing magnetic field induces the current in the squirrel-cage rotor. If the rotor is spinning at the same rate as the magnetic field, the rotor will encounter an unchanging magnetic field and there will be no current in the bars of the rotor. As a result, the rotor will not generate a magnetic field and there will be no torque to rotate it. The consequence is that the rotor must spin somewhat slower than the magnetic field. This is called "slippage" and is typically a few percent of the full speed, with more slippage as more torque is required.

Many household appliances use induction motors, but how do they generate a rotating magnetic field from a single-phase AC winding? The problem is that the magnetic field in a single AC winding will just flip back and forth, so the motor will not turn in either direction. One solution is a shaded-pole motor, which puts a copper bar around part of each pole to break the symmetry and produce a weakly rotating magnetic field. More powerful induction motors use a startup winding with a capacitor (analogous to the control winding). This winding can either be switched out of the circuit once the motor starts spinning,10 or used continuously, called a permanent-split capacitor (PSC) motor. The best solution is three-phase power (if available); a three-phase winding automatically produces a rotating magnetic field.

Tachometer/generator

The second part of the unit is the tachometer generator, sometimes called the rate unit.11 The purpose of the generator is to produce a voltage proportional to the speed of the shaft. The unusual thing about this generator is that it produces a 400-hertz output that is either in phase with the input or 180° out of phase. This is important because the phase indicates which direction the shaft is turning. Note that a "normal" generator is different: the output frequency is proportional to the speed.

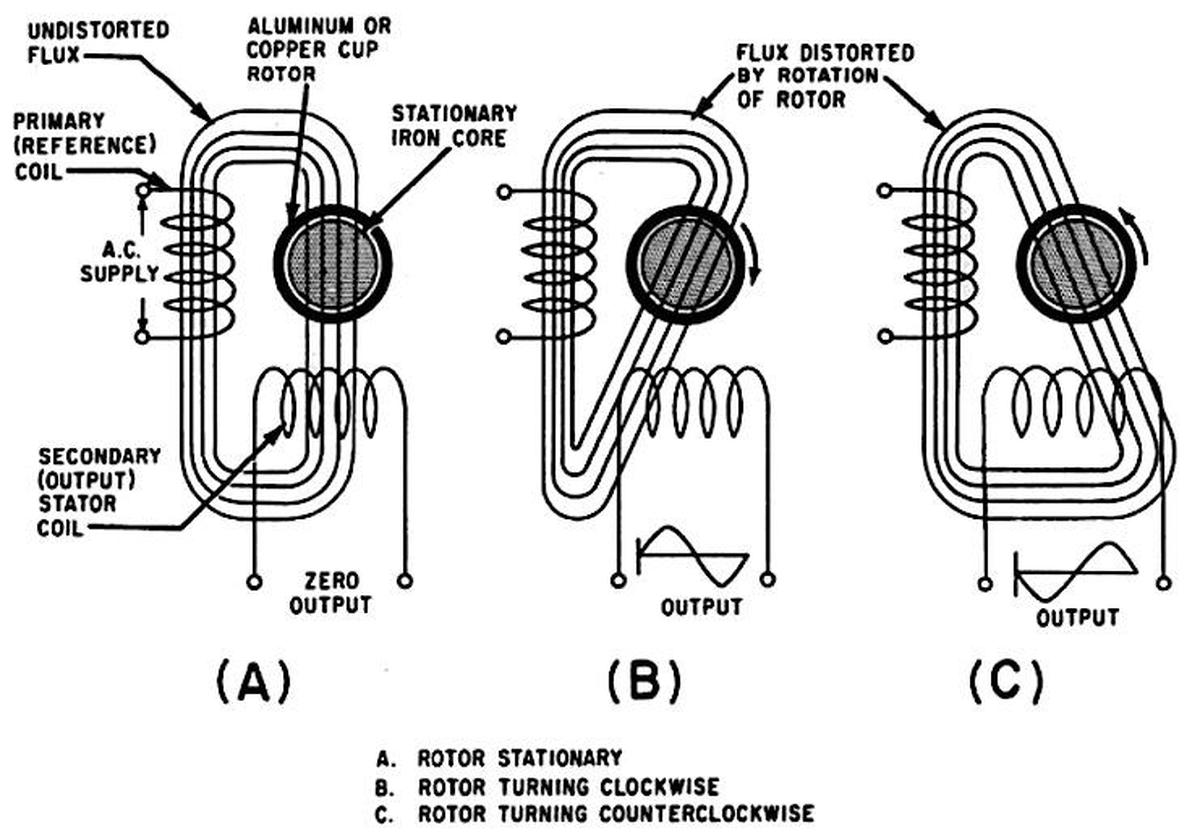
The diagram below shows the principle behind the generator. It has two stator windings: the reference coil that is powered at 400 Hz, and the output coil that produces the output signal. When the rotor is stationary (A), the magnetic flux is perpendicular to the output coil, so no output voltage is produced. But when the rotor turns (B), eddy currents in the rotor distort the magnetic field. It now couples with the output coil, producing a voltage. As the rotor turns faster, the magnetic field is distorted more, increasing the coupling and thus the output voltage. If the rotor turns in the opposite direction (C), the magnetic field couples with the output coil in the opposite direction, inverting the output phase. (This diagram is more conceptual than realistic, with the coils and flux 90° from their real orientation, so don't take it too seriously. As shown earlier, the coils are perpendicular to the rotor so the real flux lines are completely different.)

Principle of the drag-cup rate generator. From Navy electricity and electronics training series: Principles of synchros, servos, and gyros, Fig 2-16

But why does the rotating drum change the magnetic field? It's easier to understand by considering a tachometer that uses a squirrel-cage rotor instead of a drum. When the rotor rotates, currents will be induced in the squirrel cage, as described earlier with the motor. These currents, in turn, generate a perpendicular magnetic field, as before. This magnetic field, perpendicular to the orginal field, will be aligned with the output coil and will be picked up. The strength of the induced field (and thus the output voltage) is proportional to the speed, while the direction of the field depends on the direction of rotation. Because the primary coil is excited at 400 hertz, the currents in the squirrel cage and the resulting magnetic field also oscillate at 400 hertz. Thus, the output is at 400 hertz, regardless of the input speed.

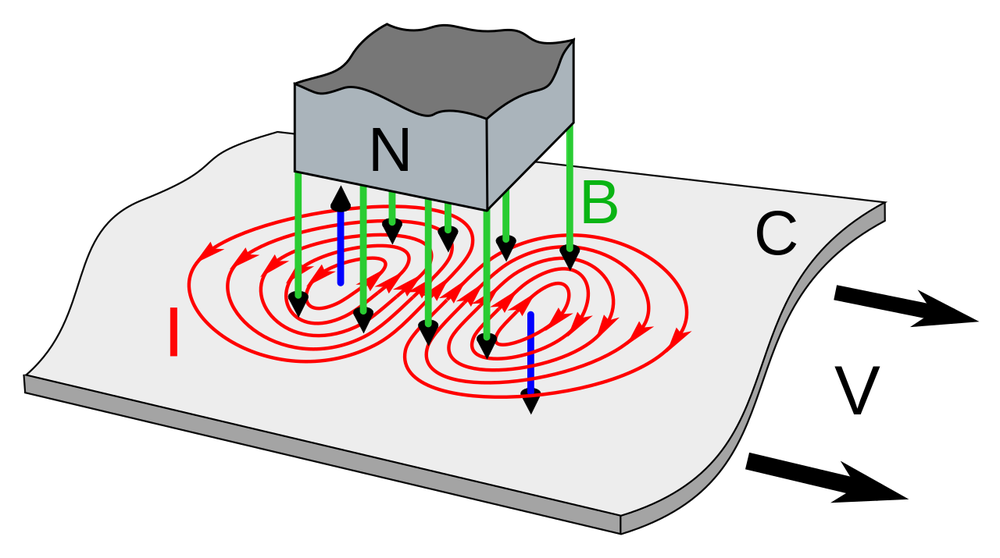
Using a drum instead of a squirrel cage provides higher accuracy because there are no fluctuations due to the discrete bars. The operation is essentially the same, except that the currents pass through the metal of the drum continuously instead of through individual bars. The result is eddy currents in the drum, producing the second magnetic field. The diagram below shows the eddy currents (red lines) from a metal plate moving through a magnetic field (green), producing a second magnetic field (blue arrows). For the rotating drum, the situation is similar except the metal surface is curved, so both field arrows will have a component pointing to the left. This creates the directed magnetic field that produces the output.

A diagram showing eddy currents in a metal plate moving under a magnet, Image from Chetvorno.

The servo loop

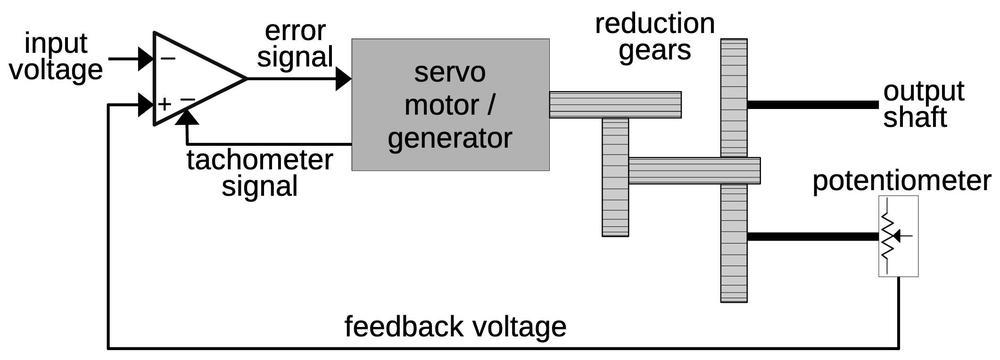
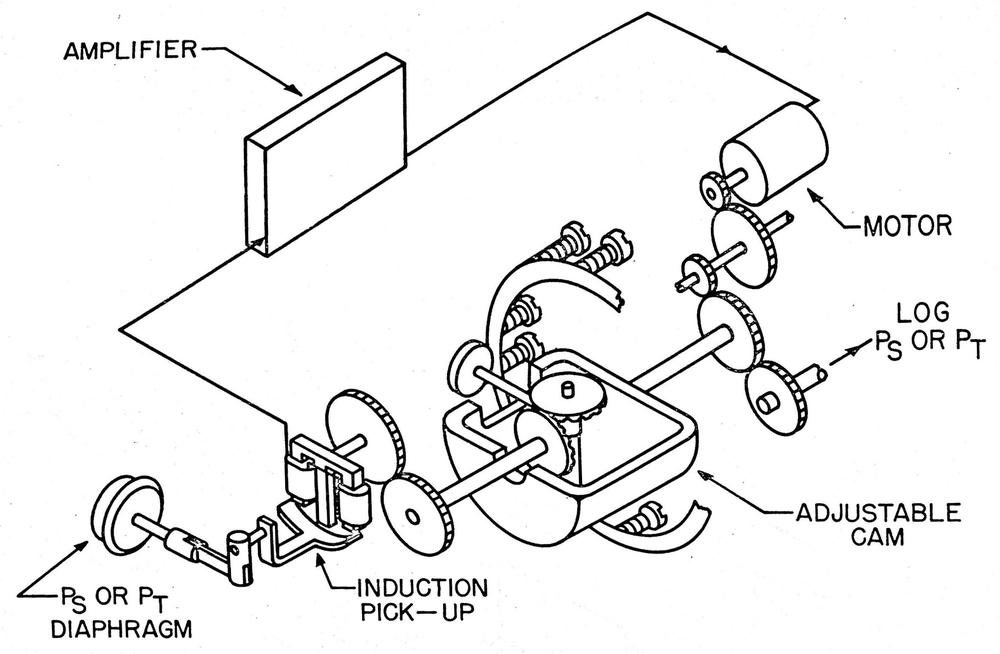
The motor/generator is called a servomotor because it is used in a servo loop, a control system that uses feedback to obtain precise positioning. In particular, the CADC uses the rotational position of shafts to represent various values. The servo loops convert the CADC's inputs (static pressure, dynamic pressure, temperature, and pressure correction) into shaft positions. The rotations of these shafts power the gears, cams, and differentials that perform the computations.

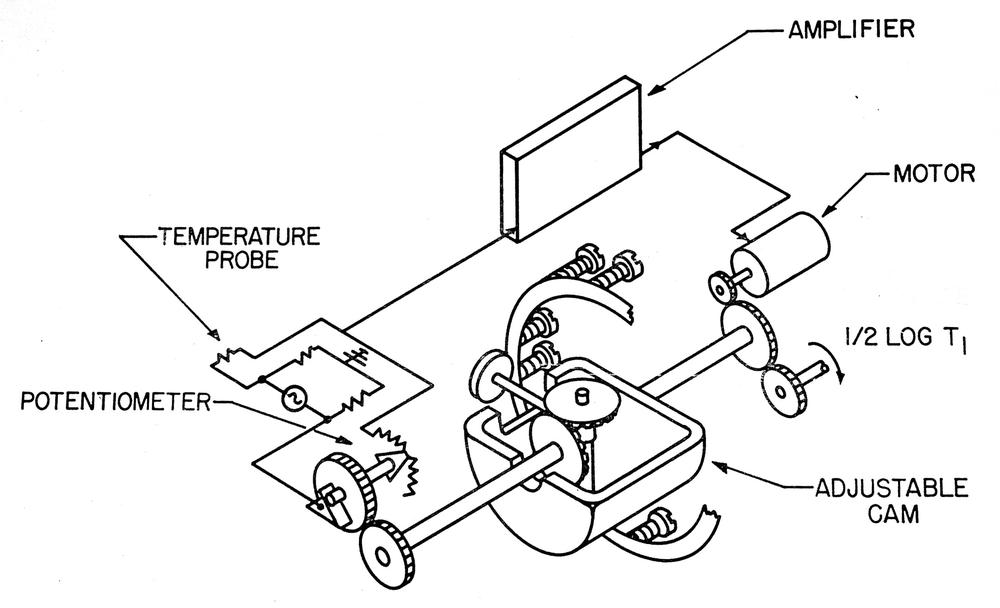
The diagram below shows a typical servo loop in the CADC. The goal is to rotate the output shaft to a position that exactly matches the input voltage. To accomplish this, the output position is converted into a feedback voltage by a potentiometer that rotates as the output shaft rotates.12 The error amplifier compares the input voltage to the feedback voltage and generates an error signal, rotating the servomotor in the appropriate direction. Once the output shaft is in the proper position, the error signal drops to zero and the motor stops. To improve the dynamic response of the servo loop, the tachometer signal is used as a negative feedback voltage. This ensures that the motor slows as the system gets closer to the right position, so the motor doesn't overshoot the position and oscillate. (This is sort of like a PID controller.)

Diagram of a servo loop in the CADC.

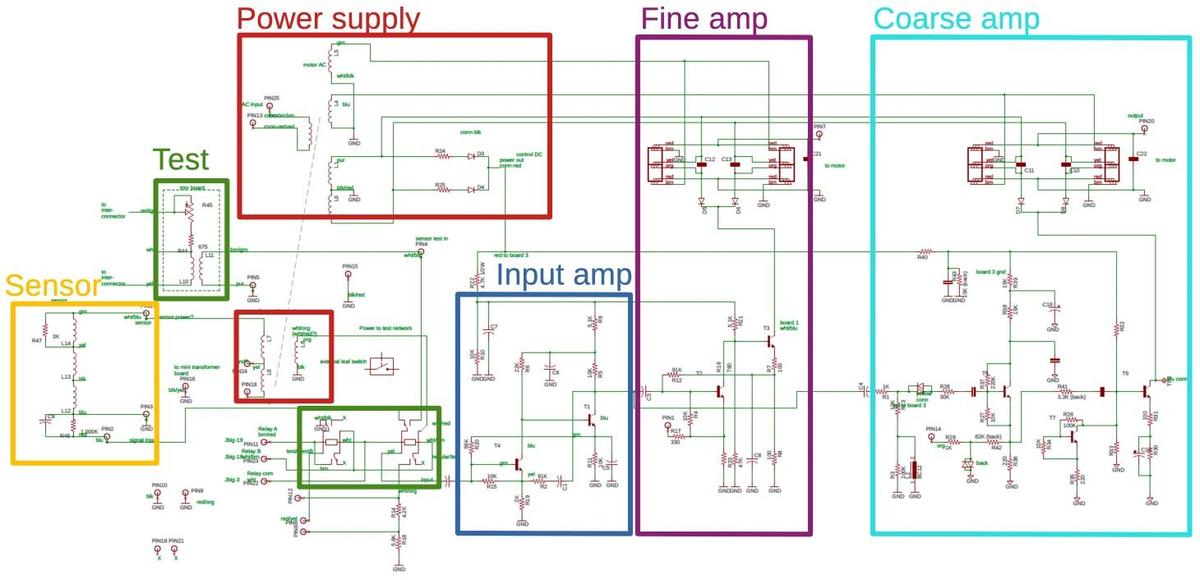
The error amplifier and motor drive circuit for a pressure transducer are shown below. Because of the state of electronics at the time, it took three circuit boards to implement a single servo loop. The amplifier was implemented with germanium transistors (since silicon transistors were later). The transistors weren't powerful enough to drive the motors directly. Instead, magnetic amplifiers (the yellow transformer-like modules at the front) powered the servomotors. The large rectangular capacitors on the right provided the phase shift required for the control voltage.

One of the three-board amplifiers for the pressure transducer.

Conclusions

The Bendix CADC used a variety of electromechanical devices including synchros, control transformers, servo motors, and tachometer generators. These were expensive military-grade components driven by complex electronics. Nowadays, you can get a PWM servo motor for a few dollars with the gearing, feedback, and control circuitry inside the motor housing. These motors are widely used for hobbyist robotics, drones, and other applications. It's amazing that servo motors have gone from specialized avionics hardware to an easy-to-use, inexpensive commodity.

A modern DC servo motor. Photo by Adafruit (CC BY-NC-SA 2.0 DEED).

Follow me on Twitter @kenshirriff or RSS for updates. I'm also on Mastodon as @oldbytes.space@kenshirriff. Thanks to Joe for providing the CADC. Thanks to Marc Verdiell for disassembling the motor.

Notes and references

1. The two types of motors in the CADC are part number "FV-101-19-A1" and part number "FV-101-5-A1" (or FV101-5A1). They are called either a "Tachometer Rate Generator" or "Tachometer Motor Generator", with both names applied to the same part number. The "19" and "5" units look the same, with the "19" used for one pressure servo loop and the "5" used everywhere else.

   The motor that I got is similar to the ones in the CADC, but shorter. The difference in size is mysterious since both have the Bendix part number FV-101-5-A1.

   For reference, the motor I disassembled is labeled:

   Cedar Division Control Data Corp. ST10162 Motor Tachometer F0: 26V C0: 26V TACH: 18V 400 CPS DSA-400-70C-4651 FSN6105-581-5331 US BENDIX FV-101-5-A1

   I wondered why the motor listed both Control Data and Bendix. In 1952, the Cedar Engineering Company was spun off from the Minneapolis Honeywell Regulator Company (better known as Honeywell, the name it took in 1964). Cedar Engineering produced motors, servos, and aircraft actuators. In 1957, Control Data bought Cedar Engineering, which became the Cedar Division of CDC. Then, Control Data acquired Bendix's computer division in 1963. Thus, three companies were involved. ↩

2. My previous articles on the CADC are:

   • Overview
   • Top section
   • Pressure transducers
   • Mach section
    ↩

3. From testing the motor, here is how I believe it is wired:
   Motor reference (power): red and black
   Motor control: blue and orange
   Generator reference (power): green and brown
   Generator out: white and yellow ↩

4. The bars on the squirrel-cage rotor are at a slight angle. Parallel bars would go in and out of alignment with the stator, causing fluctuations in the force, while the angled bars avoid this problem. ↩

5. This cross-section through the stator shows the windings. On the left, each winding is separated into the parts on either side of the pole. On the right, you can see how the wires loop over from one side of the pole to the other. Note the small circles in the 12 o'clock and 9 o'clock positions: cross sections of the input wires. The individual horizontal wires near the circumference connect alternating windings.

   

   A cross-section of the stator, formed by sanding down the plastic on the end.

    ↩

6. It's hard to find explanations of AC servomotors since they are an old technology. One discussion is in Electromechanical components for servomechanisms (1961). This book points out some interesting things about a servomotor. The stall torque is proportional to the control voltage. Servomotors are generally high-speed, but low-torque devices, heavily geared down. Because of their high speed and their need to change direction, rotational inertia is a problem. Thus, servomotors typically have a long, narrow rotor compared with typical motors. (You can see in the teardown photo that the rotor is long and narrow.) Servomotors are typically designed with many poles (to reduce speed) and smaller air gaps to increase inductance. These small airgaps (e.g. 0.001") require careful manufacturing tolerance, making servomotors a precision part. ↩

7. The principle is Faraday's law of induction: "The electromotive force around a closed path is equal to the negative of the time rate of change of the magnetic flux enclosed by the path." ↩

8. Ampère's law states that "the integral of the magnetizing field H around any closed loop is equal to the sum of the current flowing through the loop." ↩

9. The direction of the current flow (up or down) depends on the direction of rotation. I'm not going to worry about the specific direction of current flow, magnetic flux, and so forth in this article. ↩

10. Once an induction motor is spinning, it can be powered from a single AC phase since the stator is rotating with respect to the magnetic field. This works for the servomotor too. I noticed that once the motor is spinning, it can operate without the control voltage. This isn't the normal way of using the motor, though. ↩

11. A long discussion of tachometers is in the book Electromechanical Components for Servomechanisms (1961). The AC induction-generator tachometer is described starting on page 193.

    For a mathematical analysis of the tachometer generator, see Servomechanisms, Section 2, Measurement and Signal Converters, MCP 706-137, U.S. Army. This source also discusses sources of errors in detail. Inexpensive tachometer generators may have an error of 1-2%, while precision devices can have an error of about 0.1%. Accuracy is worse for small airborne generators, though. Since the Bendix CADC uses the tachometer output for damping, not as a signal output, accuracy is less important. ↩

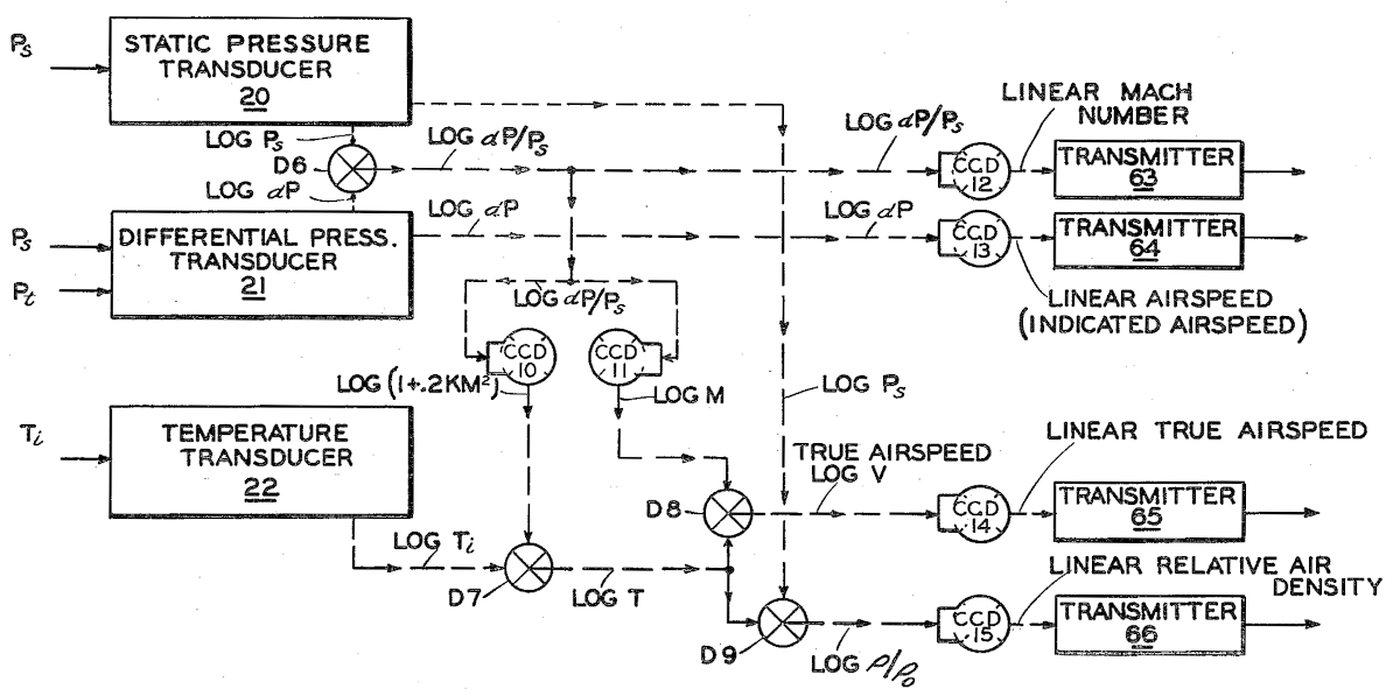
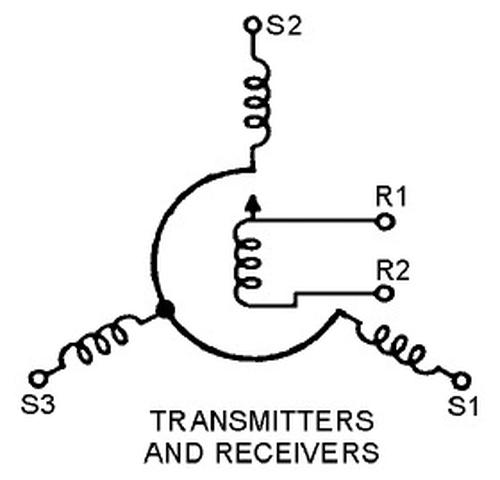
12. Different inputs in the CADC use different feedback mechanisms. The temperature servo uses a potentiometer for feedback. The angle of attack correction uses a synchro control transformer, which generates a voltage based on the angle error. The pressure transducers contain inductive pickups that generate a voltage based on the pressure error. For more details, see my article on the CADC's pressure transducer servo circuits. ↩

Inside the mechanical Bendix Air Data Computer, part 3: pressure transducers

The Bendix Central Air Data Computer (CADC) is an electromechanical analog computer that uses gears and cams for its mathematics. It was a key part of military planes such as the F-101 and the F-111 fighters, computing airspeed, Mach number, and other "air data". This article reverse-engineers the two pressure transducers, on the right in the photo below. It is part 3 of my series on the CADC.1

The Bendix MG-1A Central Air Data Computer with the case removed, showing the compact gear mechanisms inside. Click this image (or any other) for a larger version.

Aircraft have determined airspeed from air pressure for over a century. A port in the side of the plane provides the static air pressure,2 the air pressure outside the aircraft. A pitot tube points forward and receives the "total" air pressure, a higher pressure due to the speed of the airplane forcing air into the tube. The airspeed can be determined from the ratio of these two pressures, while the altitude can be determined from the static pressure.

But as you approach the speed of sound, the fluid dynamics of air change and the calculations become very complicated. With the development of supersonic fighter planes in the 1950s, simple mechanical instruments were no longer sufficient. Instead, an analog computer calculated the "air data" (airspeed, air density, Mach number, and so forth) from the pressure measurements. This computer then transmitted the air data electrically to the systems that needed it: instruments, weapons targeting, engine control, and so forth. Since the computer was centralized, such a system was called a Central Air Data Computer or CADC, manufactured by Bendix and other companies.

A closeup of the numerous gears inside the CADC. Three differential gear mechanisms are visible.

Each value in the Bendix CADC is indicated by the rotational position of a shaft. Compact electric motors rotated the shafts, controlled by magnetic amplifier servo loops. Gears, cams, and differentials performed computations, with the results indicated by more rotations. Devices called synchros converted the rotations to electrical outputs that controlled other aircraft systems. The CADC is said to contain 46 synchros, 511 gears, 820 ball bearings, and a total of 2,781 major parts (but I haven't counted). These components are crammed into a compact cylinder: 15 inches long and weighing 28.7 pounds.

The equations computed by the CADC are impressively complicated. For instance, one equation computes the Mach number $M$ from the total pressure \( P_t \) and the static pressure \( P_s \):3

\[~~~\frac{P_t}{P_s} = \frac{166.9215M^7}{( 7M^2-1)^{2.5}}\]

It seems incredible that these functions could be computed mechanically, but three techniques make this possible. The fundamental mechanism is the differential gear, which adds or subtracts values. Second, logarithms are used extensively, so multiplications and divisions become additions and subtractions performed by a differential, while square roots are calculated by gearing down by a factor of 2. Finally, specially-shaped cams implement functions: logarithm, exponential, and other one-variable functions.4 By combining these mechanisms, complicated functions can be computed mechanically.

The pressure transducers

In this article, I'm focusing on the pressure transducers and how they turn pressures into shaft rotations. The CADC receives two pressure inputs: the total pressure \( P_t \) from the pitot tube, and the static pressure \( P_s \) from the static pressure port.5 The CADC has two independent pressure transducer subsystems, one for total pressure and one for static pressure. The two pressure transducers make up the right half of the CADC. The copper pressure tube for the static pressure is visible on top of the CADC below. This tube feeds into the black-domed pressure sensor at the right. The gears, motors, and other mechanisms to the left of the pressure sensor domes generate shaft rotations that are fed into the remainder of the CADC for calculations.

Side view of the CADC.

The pressure transducer has a tricky job: it must measure tiny pressure changes, but it must also provide a rotational signal that has enough torque to rotate all the gears in the CADC. To accomplish this, the pressure transducer uses a servo loop that amplifies small pressure changes into accurate rotations. The diagram below provides an overview of the process. The pressure input causes a small movement in the bellows diaphragm. This produces a small shaft rotation that is detected by a sensitive inductive pickup. This signal is amplified and drives a motor with enough power to drive the output shaft. The motor is also geared to counteract the movement of the bellows. The result is a feedback loop so the motor's rotation tracks the air pressure, but provides much more torque. An adjustable cam corrects for any error produced by irregularities in the diaphragm response. This complete mechanism is implemented twice, once for each pressure input.

This diagram shows the structure of the transducer. From "Air Data Computer Mechanization."

To summarize, as the pressure moves the diaphragm, the induction pick-up produces an error signal. The motor is driven in the appropriate direction until the error signal becomes zero. At this point, the output shaft rotation exactly matches the input pressure. The advantage of the servo loop is that the diaphragm only needs to move the sensitive inductive pickup, rather than driving the gears of the CADC, so the pressure reading is more accurate.

In more detail, the process starts with connections from the aircraft's pitot tube and static pressure port to the CADC. The front of the CADC (below) has connections for the total pressure and the static pressure. The CADC also has five round military connectors for electrical connections between the CADC and the rest of the aircraft. (The outputs from the CADC are electrical, with synchros converting the shaft rotations into electrical representations.) Finally, a tiny time clock at the upper right keeps track of how many hours the CADC has been in operation, so it can be maintained according to schedule.

The front panel of the CADC, showing the static pressure and total pressure connections at the bottom.

The photo below shows the main components of the pressure transducer system. At the upper left, the pressure line from the CADC's front panel goes to the pressure sensor, airtight under a black dome. The error signal from the sensor goes to the amplifier, which consists of three boards. The amplifier's power transformer and magnetic amplifiers are the most visible components. The amplifier drives the motors to the left. There are two motors controlled by the amplifier: one for coarse adjustments and one for fine adjustments. By using two motors, the CADC can respond rapidly to large pressure changes, while also accurately tracking small pressure changes. Finally, the output from the motor goes through the adjustable cam in the middle before providing the feedback signal to the pressure sensor. The output from the transducer to the rest of the CADC is a shaft on the left, but it is in the middle of the CADC and isn't visible in the photo.

A closeup of the transducer, showing the main parts.

The pressure sensor

Each pressure sensor is packaged in a black airtight dome and is fed from its associated pressure line. Inside the sensor, two sealed metal bellows (below) expand or contract as the pressure changes. The bellows are connected to opposite sides of a metal shaft, which rotates as the bellows expand or contract. This shaft rotates an inductive pickup, providing the error signal. The servo loop rotates a second shaft that counteracts the rotation of the first shaft; this shaft and gears are also visible below.

Inside the pressure transducer. The two disc-shaped bellows are connected to opposite sides of a shaft so the shaft rotates as the bellows expand or contract.

The end view of the sensor below shows the inductive pickup at the bottom, with colorful wires for the input (400 Hz AC) and the output error signal. The coil visible on the inductive pickup is an anti-backlash spring to ensure that the pickup doesn't wobble back and forth. The electrical pickup coil is inside the inductive pickup and isn't visible.

Inside the transducer housing, showing the bellows and inductive pickup.

The amplifier

Each transducer feedback signal is amplified by three circuit boards centered around magnetic amplifiers, transformer-like amplifiers that were popular before high-power transistors came along. The photo below shows how the amplifier boards are packed next to the transducers. The boards are complex, filled with resistors, capacitors, germanium transistors, diodes, relays, and other components.

The pressure transducers are the two black domes at the top. The circuit boards next to each pressure transducer are the amplifiers. The yellowish transformer-like devices with three windings are the magnetic amplifiers.

I reverse-engineered the boards and created the schematic below. I'll discuss the schematic at a high level; click it for a larger version if you want to see the full circuitry. The process starts with the inductive sensor (yellow), which provides the error input signal to the amplifier. The first stage of the amplifier (blue) is a two-transistor amplifier and filter. From there, the signal goes to two separate output amplifiers to drive the two motors: fine (purple) and coarse (cyan).

Schematic of the servo amplifier, probably with a few errors. Click for a larger version.

The inductive sensor provides its error signal as a 400 Hz sine wave, with a larger signal indicating more error. The phase of the signal is 0° or 180°, depending on the direction of the error. In other words, the error signal is proportional to the driving AC signal in one direction and flipped when the error is in the other direction. This is important since it indicates which direction the motors should turn. When the error is eliminated, the signal is zero.

Each output amplifier consists of a transistor circuit driving two magnetic amplifiers. Magnetic amplifiers are an old technology that can amplify AC signals, allowing the relatively weak transistor output to control a larger AC output. The basic idea of a magnetic amplifier is a controllable inductor. Normally, the inductor blocks alternating current. But applying a relatively small DC signal to a control winding causes the inductor to saturate, permitting the flow of AC. Since the magnetic amplifier uses a small signal to control a much larger signal, it provides amplification.

In the early 1900s, magnetic amplifiers were used in applications such as dimming lights. Germany improved the technology in World War II, using magnetic amplifiers in ships, rockets, and trains. The magnetic amplifier had a resurgence in the 1950s; the Univac Solid State computer used magnetic amplifiers (rather than vacuum tubes or transistors) as its logic elements. However, improvements in transistors made the magnetic amplifier obsolete except for specialized applications. (See my IEEE Spectrum article on magnetic amplifiers for more history of magnetic amplifiers.)

In the CADC, magnetic amplifiers control the AC power to the motors. Two magnetic amplifiers are visible on top of the amplifier board stack, while two more are on the underside; they are the yellow devices that look like transformers. (Behind the magnetic amplifiers, the power transformer is labeled "A".)

One of the three-board amplifiers for the pressure transducer.

The transistor circuit generates the control signal to the magnetic amplifiers, and the output of the magnetic amplifiers is the AC signal to the motors. Specifically, the CADC uses two magnetic amplifiers for each motor. One magnetic amplifier powers the motor to spin clockwise, while the other makes the motor spin counterclockwise. The transistor circuit will pull one magnetic amplifier winding low; the phase of the input signal controls which magnetic amplifier, and thus the motor direction. (If the error input signal is zero, neither winding is pulled low, both magnetic amplifiers block AC, and the motor doesn't turn.)6 The result of this is that the motor will spin in the correct direction based on the error input signal, rotating the mechanism until the mechanical output position matches the input pressure. The motors are "Motor / Tachometer Generator" units that also generate a voltage based on their speed. This speed signal is fed into the transistor amplifier to provide negative feedback, limiting the motor speed as the error becomes smaller and ensuring that the feedback loop doesn't overshoot.

The other servo loops in the CADC (temperature and position error correction) have one motor driver constructed from transistors and two magnetic amplifiers. However, each pressure transducer has two motor drivers (and thus four magnetic amplifiers), one for fine adjustment and one for coarse adjustment. This allows the servo loop to track the input pressure very closely, while also adjusting rapidly to larger changes in pressure. The coarse amplifier uses back-to-back diodes to block small changes; only input voltages larger than a diode drop will pass through and energize the coarse amplifier.

The CADC is powered by standard avionics power of 115 volts AC, 400 hertz. Each pressure transducer amplifier has a simple power supply running off this AC, using a multi-winding power transformer. A center-tapped winding and full wave rectifier produces DC for the transistor amplifiers. Other windings supply AC (controlled by the magnetic amplifiers) to power the motors, AC for the magnetic amplifier control signals, and AC for the sensor. The transformer ensures that the transducer circuitry is electrically isolated from other parts of the CADC and the aircraft. The power supply is indicated in red in the schematic above.

The schematic also shows test circuitry (blue). One of the features of the CADC is that it can be set to two test configurations before flight to ensure that the system is operating properly and is correctly calibrated.7 Two relays allow the pressure transducer to switch to one of two test inputs. This allows the CADC to be checked for proper operation and calibration. The test inputs are provided from an external board and a helical feedback potentiometer (Helipot) that provides simulated sensor input.

Getting the amplifiers to work was a challenge. Many of the capacitors in the CADC had deteriorated and failed, as shown below. Marc went through the CADC boards and replaced the bad capacitors. However, one of the pressure transducer boards still failed to work. After much debugging, we discovered that one of the new capacitors had also failed. Finally, after replacing that capacitor a second time, the CADC was operational.

Some bad capacitors in the CADC. This is the servo amplifier for the temperature sensor.

The mechanical feedback loop

The amplifier boards energize two motors that rotate the output shaft,8 the coarse and fine motors. The outputs from the coarse and fine motors are combined through a differential gear assembly that sums its two input rotations.9 While the differential functions like the differential in a car, it is constructed differently, with a spur-gear design. This compact arrangement of gears is about 1 cm thick and 3 cm in diameter. The differential is mounted on a shaft along with three co-axial gears: two gears provide the inputs to the differential and the third provides the output. In the photo, the gears above and below the differential are the input gears. The entire differential body rotates with the sum, connected to the output gear at the top through a concentric shaft. The two thick gears inside the differential body are part of its mechanism.

A closeup of a differential mechanism.

(Differential gear assemblies are also used as the mathematical component of the CADC, as it performs addition or subtraction. Since most values in the CADC are expressed logarithmically, the differential computes multiplication and division when it adds or subtracts its inputs.)

The CADC uses cams to correct for nonlinearities in the pressure sensors. The cam consists of a warped metal plate. As the gear rotates, a spring-loaded vertical follower moves according to the shape of the plate. The differential gear assembly under the plate adds this value to the original input to obtain a corrected value. (This differential implementation is different from the one described above.) The output from the cam is fed into the pressure sensor, closing the feedback loop.

The corrector cam is adjusted to calibrate the output to counteract for variations in the bellows behavior.

At the top, 20 screws can be rotated to adjust the shape of the cam plate and thus the correction factor. These cams allow the CADC to be fine-tuned to maximize accuracy. According to the spec, the required accuracy for pressure was "40 feet or 0.15 percent of attained altitude, whichever is greater."

Conclusions

The Bendix CADC was built at an interesting point in time, when computations could be done digitally or analog, mechanically or electrically. Because the inputs were analog and the desired outputs were analog, the decision was made to use an analog computer for the CADC. Moreover, transistors were available but their performance was limited. Thus, the servo amplifiers are built from a combination of transistors and magnetic amplifiers.

Modern air data computers are digital but they are still larger than you might expect because they need to handle physical pressure inputs. While a drone can use a tiny 5mm MEMS pressure sensor, air data computers for aircraft have higher requirements and typically use larger vibrating cylinder pressure sensors. Even so, at 45 mm long, the modern pressure sensor is dramatically smaller than the CADC's pressure transducer with its metal-domed bellows sensor, three-board amplifier, motors, cam, and gear train. Although the mechanical Bendix CADC seems primitive, this CADC was used by the Air Force until the 1980s. I guess if the system worked, there was no reason to update it.

I plan to continue reverse-engineering the Bendix CADC,10 so follow me on Twitter @kenshirriff or RSS for updates. I'm also on Mastodon as @oldbytes.space@kenshirriff. Thanks to Joe for providing the CADC. Thanks to Nancy Chen for obtaining a hard-to-find document for me. Marc Verdiell and Eric Schlaepfer are working on the CADC with me.

Notes and references

1. My previous posts on the CADC provide an overview and reverse-engineering of the left side. Much of the background of this article is copied from the previous articles, if it looks familiar. ↩

2. The static air pressure can also be provided by holes in the side of the pitot tube. I couldn't find information indicating exactly how the planes with the CADC received static pressure. ↩

3. Although the CADC's equations may seem ad hoc, they can be derived from fluid dynamics principles. These equations were standardized in the 1950s by various government organizations including the National Bureau of Standards and NACA (the precursor of NASA). ↩

4. The CADC also uses cams to implement functions such as logarithms, exponentials, and complicated functions of one variable such as ${M}/{\sqrt{1 + .2 M^2}}$. These cams have a completely different design from the corrector cams. The function cams are fixed shape, unlike the adjustable corrector cams. The function is encoded into the cam's shape during manufacturing, so implementing a hard-to-compute nonlinear function isn't a problem for the CADC. The photo below shows a cam with the follower arm in front. As the cam rotates, the follower moves in and out according to the cam's radius. The pressure transducers do not use fixed cams, so I won't discuss them more in this article.

   

   A cam inside the CADC implements a function.

    ↩

5. The CADC also has an input for the "position error correction". This input provides a correction factor because the measured static pressure may not exactly match the real static pressure. The problem is that the static pressure is measured from a port on the aircraft. Distortions in the airflow may cause errors in this measurement. A separate box, the "compensator", determined the correction factor based on the angle of attack and fed it to the CADC as a synchro signal. The position error correction is applied in a separate section of the CADC, downstream from the transducers, so I will ignore it for this article. ↩

6. A bit more explanation of the transistor circuit driving the magnetic amplifier. The idea is that one magnetic amplifier or the other is selected, depending on the phase of the error signal, causing the motor to turn counterclockwise or clockwise as needed. To implement this, the magnetic amplifier control windings are connected to opposite phases of the 400 Hz power. The transistor is connected to both magnetic amplifiers through diodes, so current will flow only if the transistor pulls the winding low during the half-cycle that the winding is powered high. Thus, depending on the phase of the transistor output, one winding or the other will be powered, allowing that magnetic amplifier to pass AC to the motor. ↩

7. According to the specification, the CADC has simulated "low point" and "high point" test conditions. The low point is 11,806 feet altitude, 1064 ft/sec true airspeed, Mach .994, total temperature 317.1 °K, and density × speed of sound of 1.774 lb sec/ft³. The high point is 50,740 feet altitude, 1917 ft/sec true airspeed, Mach 1.980, total temperature 366.6 °K, and density × speed of sound of .338 lb sec/ft³. ↩

8. The motor part number is Bendix FV101-5A1. ↩

9. Strictly speaking, the output of the differential is the sum of the inputs divided by two. I'm ignoring the factor of 2 because the gear ratios can easily cancel it out. It's also arbitrary whether you think of the differential as adding or subtracting, since it depends on which rotation direction is defined as positive. ↩

10. It was very difficult to find information about the CADC. The official military specification is MIL-C-25653C(USAF). After searching everywhere, I was finally able to get a copy from the Technical Reports & Standards unit of the Library of Congress. The other useful document was in an obscure conference proceedings from 1958: "Air Data Computer Mechanization" (Hazen), Symposium on the USAF Flight Control Data Integration Program, Wright Air Dev Center US Air Force, Feb 3-4, 1958, pp 171-194. ↩

Reverse-engineering an electromechanical Central Air Data Computer

Determining the airspeed and altitude of a fighter plane is harder than you'd expect. At slower speeds, pressure measurements can give the altitude, air speed, and other "air data". But as planes approach the speed of sound, complicated equations are needed to accurately compute these values. The Bendix Central Air Data Computer (CADC) solved this problem for military planes such as the F-101 and the F-111 fighters, and the B-58 bomber.1 This electromechanical marvel was crammed full of 1955 technology: gears, cams, synchros, and magnetic amplifiers. In this blog post I look inside the CADC, describe the calculations it performed, and explain how it performed these calculations mechanically.

The Bendix MG-1A Central Air Data Computer with the case removed, showing the complex mechanisms inside. Click this image (or any other) for a larger version.

This analog computer performs calculations using rotating shafts and gears, where the angle of rotation indicates a numeric value. Differential gears perform addition and subtraction, while cams implement functions. The CADC is electromechanical, with magnetic amplifiers providing feedback signals and three-phase synchros providing electrical outputs. It is said to contain 46 synchros, 511 gears, 820 ball bearings, and a total of 2,781 major parts. The photo below shows a closeup of the gears.

A closeup of the complex gears inside the CADC,

What it does

For over a century, aircraft have determined airspeed from air pressure. A port in the side of the plane provides the static air pressure,2 which is the air pressure outside the aircraft. A pitot tube points forward and receives the "total" air pressure, a higher pressure due to the speed of the airplane forcing air into the tube. (In the photo below, you can see the long pitot tube sticking out from the nose of a F-101.) The airspeed can be determined from the ratio of these two pressures, while the altitude can be determined from the static pressure.

The F-101 "Voodoo", USAF photo.

But as you approach the speed of sound, the fluid dynamics of air change and the calculations become very complicated. With the development of supersonic fighter planes in the 1950s, simple mechanical instruments were no longer sufficient. Instead, an analog computer to calculate the "air data" (airspeed, altitude, and so forth) from the pressure measurements. One option would be for each subsystem (instruments, weapons control, engine control, etc) to compute the air data separately. However, it was more efficient to have one central system perform the computation and provide the data electrically to all the subsystems that need it. This system was called a Central Air Data Computer or CADC.

The Bendix CADC has two pneumatic inputs through tubes: the static pressure3 and the total pressure. It also receives the total temperature from a platinum temperature probe. From these, it computes many outputs: true air speed, Mach number, log static pressure, differential pressure, air density, air density × the speed of sound, total temperature, and log true free air temperature.

The CADC implemented a surprisingly complex set of functions derived from fluid dynamics equations describing the behavior of air at various speeds and conditions. First, the Mach number is computed from the ratio of total pressure to static pressure. Different equations are required for subsonic and supersonic flight. Although this equation looks difficult to solve mathematically, fundamentally M is a function of one variable ($P_t / P_s$), and this function is encoded in the shape of a cam. (You are not expected to understand the equations below. They are just to illustrate the complexity of what the CADC does.)

\[M<1:\] \[~~~\frac{P_t}{P_s} = ( 1+.2M^2)^{3.5}\]

\[M > 1:\]

\[~~~\frac{P_t}{P_s} = \frac{166.9215M^7}{( 7M^2-1)^{2.5}}\]

Next, the temperature is determined from the Mach number and the temperature indicated by a temperature probe.

\[T = \frac{T_{ti}}{1 + .2 M^2} \]

The indicated airspeed and other outputs are computed in turn, but I won't go through all the equations. Although these equations may seem ad hoc, they can be derived from fluid dynamics principles. These equations were standardized in the 1950s by various government organizations including the National Bureau of Standards and NACA (the precursor of NASA). While the equations are complicated, they can be computed with mechanical means.

How it is implemented

The Air Data Computer is an analog computer that determines various functions of the static pressure, total pressure and temperature. An analog computer was selected for this application because the inputs are analog and the outputs are analog, so it seemed simplest to keep the computations analog and avoid conversions. The computer performs its computations mechanically, using the rotation angle of shafts to indicate values. For the most part, values are represented logarithmically, which allows multiplication and division to be implemented by adding and subtracting rotations. A differential gear mechanism provides the underlying implementation of addition and subtraction. Specially-shaped cams provide the logarithmic and exponential conversions as necessary. Other cams implement various arbitrary functions.

The diagram below, from patent 2,969,210, shows some of the operations. At the left, transducers convert the pressure and temperature inputs from physical quantities into shaft rotations, applying a log function in the process. Subtracting the two pressures with a differential gear mechanism (X-in-circle symbol) produces the log of the pressure ratios. Cam "CCD 12" generates the Mach number from this log pressure ratio, still expressed as a shaft rotation. A synchro transmitter converts the shaft rotation into a three-phase electrical output from the CADC. The remainder of the diagram uses more cams and differentials to produce the other outputs. Next, I'll discuss how these steps are implemented.

A diagram showing how values are computed by the CADC. Source: Patent 2969910.

The pressure transducer

The CADC receives the static and total pressure through tubes connected to the front of the CADC. (At the lower right, one of these tubes is visible.) Inside the CADC, two pressure transducers convert the pressures into rotational signals. The pressure transducers are the black domed cylinders at the top of the CADC.

The pressure transducers are the two black domes at the top. The circuit boards next to each pressure transducer are the amplifiers. The yellowish transformer-like devices with three windings are the magnetic amplifiers.

Each pressure transducer contains a pair of bellows that expand and contract as the applied pressure changes. They are connected to opposite sides of a shaft so they cause small rotations of the shaft.

Inside the pressure transducer. The two disc-shaped bellows are connected to opposite sides of a shaft so the shaft rotates as the bellows expand or contract.

The pressure transducer has a tricky job: it must measure tiny pressure changes, but it must also provide a rotational signal that has enough torque to rotate all the gears in the CADC. To accomplish this, the pressure transducer uses a servo loop. The bellows produce a small shaft motion that is detected by an inductive pickup. This signal is amplified and drives a motor with enough power to move all the gears. The motor is also geared to counteract the movement of the bellows. This creates a feedback loop so the motor's rotation tracks the air pressure, but provides much more force. A cam is used so the output corresponds to the log of the input pressure.

This diagram shows the structure of the transducer. From "Air Data Computer Mechanization."

Each transducer signal is amplified by three circuit boards centered around a magnetic amplifier, a transformer-like amplifier circuit that was popular before high-power transistors came along. The photo below shows how the amplifier boards are packed next to the transducers. The boards are complex, filled with resistors, capacitors, germanium transistors, diodes, relays, and other components.

This end-on view of the CADC shows the pressure transducers, the black cylinders. Next to each pressure transducer is a complex amplifier consisting of multiple boards with transistors and other components. The magnetic amplifiers are the yellowish transformer-like components.

Temperature

The external temperature is an important input to the CADC since it affects the air density. A platinum temperature probe provides a resistance4 that varies with temperature. The resistance is converted to rotation by an electromechanical transducer mechanism. Like the pressure transducer, the temperature transducer uses a servo mechanism with an amplifier and feedback loop. For the temperature transducer, though, the feedback signal is generated by a resistance bridge using a potentiometer driven by the motor. By balancing the potentiometer's resistance with the platinum probe's resistance, a shaft rotation is produced that corresponds to the temperature. The cam is configured to produce the log of the temperature as output.

This diagram shows the structure of the temperature transducer. From "Air Data Computer Mechanization."

The temperature transducer section of the CADC is shown below. The feedback potentiometer is the red cylinder at the lower right. Above it is a metal-plate adjustment cam, which will be discussed below. The CADC is designed in a somewhat modular way, with the temperature section implemented as a removable wedge-shaped unit, the lower two-thirds of the photo. The temperature transducer, like the pressure transducer, has three boards of electronics to implement the feedback amplifier and drive the motor.

The temperature transducer section of the CADC.

The differential

The differential gear assembly is a key component of the CADC's calculations, as it performs addition or subtraction of rotations: the rotation of the output shaft is the sum or difference of the input shafts, depending on the direction of rotation.5 When rotations are expressed logarithmically, addition and subtraction correspond to multiplication and division. This differential is constructed as a spur-gear differential. It has inputs at the top and bottom, while the body of the differential rotates to produce the sum. The two visible gears in the body mesh with the internal input gears, which are not visible. The output is driven by the body through a concentric shaft.

A closeup of a differential mechanism.

The cams

The CADC uses cams to implement various functions. Most importantly, cams perform logarithms and exponentials. Cams also implement more complex functions of one variable such as ${M}/{\sqrt{1 + .2 M^2}}$. The photo below shows a cam (I think exponential) with the follower arm in front. As the cam rotates, the follower moves in and out according to the cam's radius, providing the function value.

A cam inside the CADC implements a function.

The cams are combined with a differential in a clever way to make the cam shape more practical, as shown below.6 The input (23) drives the cam (30) and the differential (37-41). The follower (32) tracks the cam and provides a second input (35) to the differential. The sum from the differential produces the output (26).

This diagram, from Patent 2969910, shows how the cam and follower are connected to a differential.

The warped plate cam

Some functions are implemented by warped metal plates acting as cams. This type of cam can be adjusted by turning the 20 setscrews to change the shape of the plate. A follower rides on the surface of the cam and provides an input to a differential underneath the plate. The differential adds the cam position to the input rotation, producing a modified rotation, as with the solid cam. The pressure transducer, for instance, uses a cam to generate the desired output function from the bellows deflection. By using a cam, the bellows can be designed for good performance without worrying about its deflection function.

A closeup of a warped-plate cam.

The synchro outputs

Most of the outputs from the CADC are synchro signals.7 A synchro is an interesting device that can transmit a rotational position electrically over three wires. In appearance, a synchro is similar to an electric motor, but its internal construction is different, as shown below. In use, two synchros have their stator windings connected together, while the rotor windings are driven with AC. Rotating the shaft of one synchro causes the other to rotate to the same position. I have a video showing synchros in action here.

Cross-section diagram of a synchro showing the rotor and stators.

Internally, a synchro has a moving rotor winding and three fixed stator windings. When AC is applied to the rotor, voltages are developed on the stator windings depending on the position of the rotor. These voltages produce a torque that rotates the synchros to the same position. In other words, the rotor receives power (26 V, 400 Hz in this case), while the three stator wires transmit the position. The diagram below shows how a synchro is represented schematically, with rotor and stator coils.

The schematic symbol for a synchro.

Before digital systems, synchros were very popular for transmitting signals electrically through an aircraft. For instance, a synchro could transmit an altitude reading to a cockpit display or a targeting system. For the CADC, most of the outputs are synchro signals, which convert the rotational values of the CADC to electrical signals. The three stator windings from the synchro inside the CADC are wired to an external synchro that receives the rotation. For improved resolution, many of these outputs use two synchros: a coarse synchro and a fine synchro. The two synchros are typically geared in an 11:1 ratio, so the fine synchro rotates 11 times as fast as the coarse synchro. Over the output range, the coarse synchro may turn 180°, providing the approximate output, while the fine synchro spins multiple times to provide more accuracy.

The front of the CADC has multiple output synchros with anti-backlash springs.

The air data system

The CADC is one of several units in the system, as shown in the block diagram below.8 The outputs of the CADC go to another box called the Air Data Converter, which is the interface between the CADC and the aircraft systems that require the air data values: fire control, engine control, navigation system, cockpit display instruments, and so forth. The motivation for this separation is that different aircraft types have different requirements for signals: the CADC remains the same and only the converter needed to be customized. Some aircraft required "up to 43 outputs including potentiometers, synchros, digitizers, and switches."

This block diagram shows how the Air Data Computer integrates with sensors and other systems. The unlabeled box on the right is the converter. From MIL-C-25653C(USAF).

The CADC was also connected to a cylindrical unit called the "Static pressure and angle of attack compensator." This unit compensates for errors in static pressure measurements due to the shape of the aircraft by producing the "position error correction". Since the compensation factor depended on the specific aircraft type, the compensation was computed outside the Central Air Data Computer, again keeping the CADC generic. This correction factor depends on the Mach number and angle of attack, and was implemented as a three-dimensional cam. The cam's shape (and thus the correction function) was determined empirically, rather than from fundamental equations.

The CADC was wired to other components through five electrical connectors as shown in the photo below.9 At the bottom are the pneumatic connections for static pressure and total pressure. At the upper right is a small elapsed time meter.

The front of the CADC has many mil-spec round connectors.

Conclusions

The Bendix MG-1A Central Air Data Computer is an amazingly complex piece of electromechanical hardware. It's hard to believe that this system of tiny gears was able to perform reliable computations in the hostile environment of a jet plane, subjected to jolts, accelerations, and vibrations. But it was the best way to solve the problem at the time,10 showing the ingenuity of the engineers who developed it.

The CADC inside its case. From the outside, its mechanical marvels are hidden.

I plan to continue reverse-engineering the Bendix CADC and hope to get it operational,11 so follow me on Twitter @kenshirriff or RSS for updates. I've also started experimenting with Mastodon recently as @oldbytes.space@kenshirriff. Until then, you can check out CuriousMarc's video below to see more of the CADC. Thanks to Joe for providing the CADC. Thanks to Nancy Chen for obtaining a hard-to-find document for me.

Notes and references

1. I haven't found a definitive list of which planes used this CADC. Based on various sources, I believe it was used in the F-86, F-101, F-104, F-105, F-106, and F-111, and the B-58 bomber. ↩

2. The static air pressure can also be provided by holes in the side of the pitot tube. I couldn't find information indicating exactly how these planes received static pressure. ↩

3. The CADC also has an input for the "position error correction". This provides a correction factor because the measured static pressure may not exactly match the real static pressure. The problem is that the static pressure is measured from a port on the aircraft. Distortions in the airflow may cause errors in this measurement. A separate box, the "compensator", determines the correction factor based on the angle of attack. ↩

4. The platinum temperature probe is type MA-1, defined by specification MIL-P-25726. It apparently has a resistance of 50 Ω at 0 °C. ↩

5. Strictly speaking, the output of the differential is the sum of the inputs divided by two. I'm ignoring the factor of 2 because the gear ratios can easily cancel it out. ↩

6. Cams are extensively used in the CADC to implement functions of one variable, including exponentiation and logarithms. The straightforward way to use a cam is to read the value of the function off the cam directly, with the radius of the cam at each angle representing the value. This approach encounters a problem when the cam wraps around, since the cam's profile will suddenly jump from one value to another. This poses a problem for the cam follower, which may get stuck on this part of the cam unless there is a smooth transition zone. Another problem is that the cam may have a large range between the minimum and maximum outputs. (Consider an exponential output, for instance.) Scaling the cam to a reasonable size will lose accuracy in the small values. The cam will also have a steep slope for the large values, making it harder to track the profile.

   The solution is to record the difference between the input and the output in the cam. A differential then adds the input value to the cam value to produce the desired value. The clever part is that by scaling the input so it matches the output at the start and end of the range, the difference function drops to zero at both ends. Thus, the cam profile matches when the angle wraps around, avoiding the sudden transition. Moreover, the difference between the input and the output is much smaller than the raw output, so the cam values can be more accurate. (This only works because the output functions are increasing functions; this approach wouldn't work for a sine function, for instance.)

   

   This diagram, from Patent 2969910, shows how a cam implements a complex function.

   The diagram above shows how this works in practice. The input is \(log~ dP/P_s\) and the output is \(log~M / \sqrt{1+.2KM^2}\). (This is a function of Mach number used for the temperature computation; K is 1.) The small humped curve at the bottom is the cam correction. Although the input and output functions cover a wide range, the difference that is encoded in the cam is much smaller and drops to zero at both ends. ↩

7. The US Navy made heavy use of synchros for transmitting signals throughout ships. The synchro diagrams are from two US Navy publications: US Navy Synchros (1944) and Principles of Synchros, Servos, and Gyros (2012). These are good documents if you want to learn more about synchros. The diagram below shows how synchros could be used on a ship.

   

   A Navy diagram illustrating synchros controlling a gun on a battleship.

    ↩

8. To summarize the symbols, the outputs are: log T_FAT: true free air temperature (the ambient temperature without friction and compression); log P_s: static pressure; M: Mach number; Q_c: differential pressure; ρ: air density; ρa: air density times the speed of sound; V_t: true airspeed. T_t: total temperature (higher due to compression of the air). Inputs are: T_T: total temperature (higher due to compression of the air). P_ti: indicated total pressure (higher due to velocity); P_si: indicated static pressure; log P_si/P_s: the position error correction from the compensator. The compensator uses input α_i: angle of attack; and produces α_T: true angle of attack; a_T: speed of sound. ↩

9. The electrical connectors on the CADC have the following functions: J614: outputs to the converter, J601: outputs to the converter, J603: AC power (115 V, 400 Hz), J602: to/from the compensator, and J604: input from the temperature probe. ↩

10. An interesting manual way to calculate air data was with a circular slide rule, designed for navigation and air data calculation. It gave answers for various combinations of pressure, temperature, Mach number, true airspeed, and so forth. See the MB-2A Air Navigation Computer instructions for details. Also see patent 2528518. I'll also point out that from the late 1800s through the 1940s and on, the term "computer" was used for any sort of device that computed a value, from an adding machine to a slide rule (or even a person). The meaning is very different from the modern usage of "computer". ↩

11. It was very difficult to find information about the CADC. The official military specification is MIL-C-25653C(USAF). After searching everywhere, I was finally able to get a copy from the Technical Reports & Standards unit of the Library of Congress. The other useful document was in an obscure conference proceedings from 1958: "Air Data Computer Mechanization" (Hazen), Symposium on the USAF Flight Control Data Integration Program, Wright Air Dev Center US Air Force, Feb 3-4, 1958, pp 171-194. ↩